Title: [ΣΑΕ Ι] Παλιά θέματα (BOARD ΑΠΟ ΠΑΝΩ)
Post by: dim on July 19, 2005, 03:01:02 am
Μην αναζητείτε και μην ανεβάζετε παλιά θέματα και σημειώσεις εδώ.
Χρησιμοποιείστε τον τομέα Downloads που φτιάχτηκε για αυτόν το σκοπό.
Έτσι βοηθάτε στην καλύτερη κατηγοριοποίησή τους
και στην διευκόλυνση της εύρεσής τους.
edit: year
Χρησιμοποιείστε τον τομέα Downloads που φτιάχτηκε για αυτόν το σκοπό.
Έτσι βοηθάτε στην καλύτερη κατηγοριοποίησή τους
και στην διευκόλυνση της εύρεσής τους.
Επειδή το topic ήταν χαώδες, 70+ σελίδες, γίνεται μια προσπάθεια να χωριστούν τα θέματα σ' ένα νέο board (https://www.thmmy.gr/smf/index.php?board=575.0) με βάση την χρονιά εξέτασης. Προς το παρόν, δεν έχουν γίνει όλες οι χρονιές, αλλά για όσες υπάρχουν να γράφετε σε εκείνα τα topics, ώστε να υπάρχει μια οργάνωση στις απορίες αλλά και στα λυμένα που ανεβαίνουν.
Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
Δεν γράφουμε εδώ για θέματα πριν το 2022 γιατί έχουμε νέο board (https://www.thmmy.gr/smf/index.php?board=575.0) Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
edit: year
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JAs0n-X on November 30, 2005, 01:42:43 am
Παιδια σημερα ηταν η Α προοδος στα ΚΑΕ...
τα θεματα δεν μας τα κρατησανε και τα εχουμε μαζι μας.
Τα εχω και εγω. Μπορω να βρω να τα σκαναρω απλα πρωτα να ρωτησω κατι...
υπαρχει κανεις που να τα εχει σχετικα καθαρα?...γιατι εγω σε μερικα σημεια τα εχω κανει μπουρδελο!
αν μπορει ας τα σκαναρει και ας τα ανεβασει στα Downloads..
αν οχι θα τα ανεβασω εγω!
τα θεματα δεν μας τα κρατησανε και τα εχουμε μαζι μας.
Τα εχω και εγω. Μπορω να βρω να τα σκαναρω απλα πρωτα να ρωτησω κατι...
υπαρχει κανεις που να τα εχει σχετικα καθαρα?...γιατι εγω σε μερικα σημεια τα εχω κανει μπουρδελο!
αν μπορει ας τα σκαναρει και ας τα ανεβασει στα Downloads..
αν οχι θα τα ανεβασω εγω!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: BOBoMASTORAS on November 30, 2005, 13:41:49 pm
κοίτα εγώ έχω scanner και μπορώ να τα ανεβάσω αλλά όπως είπες είναι λίγο ότι να ναι με τις σημειώσεις-πράξεις μου πάνω. Θα περιμένω μέχρι το απόγευμα του έχουμε ΚΑΕ αν μας πει τις απαντήσεις να τις ανεβάσω και αυτές μαζί.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JAs0n-X on December 08, 2005, 00:33:44 am
Ανεβηκαν τα θεματα της 1ης προοδου 2005 με τις λυσεις τους στον τομεα Downloads.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JAs0n-X on January 18, 2006, 15:26:59 pm
Ανέβηκαν τα θέματα της 2ης προοδου 2005-6 με τις λυσεις τους στον τομεα Downloads.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JAs0n-X on January 31, 2006, 21:14:56 pm
Ανέβηκαν τα θέματα εξετάσεων 31/1/2006 στον τομέα Downloads!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sakaflias7 on February 07, 2009, 00:23:52 am
φλεβαρη 2001 εχει λυσει κανεις στο 1ο τη συναρτηση μεταφορας και 2ο 8εμα το ΓΤΡ??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Γιώργος on February 07, 2009, 02:18:12 am
Α, να κάτι να ξεχάσω τις βλαμμένες ενεργειακές εργασίες που 'χω να κάνω! :D
Για το θέμα 1ο αρχικά διαλέγεις ένα διάνυσμα κατάστασης. Αν θυμάσαι απ' τα Κυκλώματα, ένα εύκολο διάνυσμα κατάστασης - και σίγουρο - είναι οι τάσεις των πυκνωτών και τα ρεύματα των πηνίων.
Δηλαδή: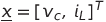
Εδώ έχεις μικρό κυκλωματάκι, οπότε μπορείς να πας λίγο στα.. τυφλά. Πάνω-κάτω να θυμάσαι ότι πρέπει να κάνεις τουλάχιστον ένα νόμο τάσεων για την τάση του πηνίου κι ένα νόμο ρευμάτων για το ρεύμα του πηνίου (πάνε "ανάποδα" θα δεις γιατί). Για μεγαλύτερα κυκλώματα, υπάρχει πιο συστηματική μέθοδος και είναι στο κεφάλαιο των εξισώσεων κατάστασης του Β' τόμου των Κυκλωμάτων: επίλυση με γράφους. Τα λέει αρκετά καλά. ;)
Έχεις:
---------------------------------------
1)ΝΡΚ:
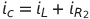
Όμως:
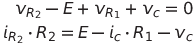
Αντικαθιστώντας:
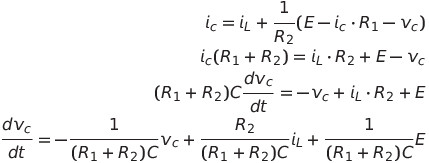
Αυτή είναι η πρώτη σχέση.
---------------------------------------
2)ΝΤΚ:
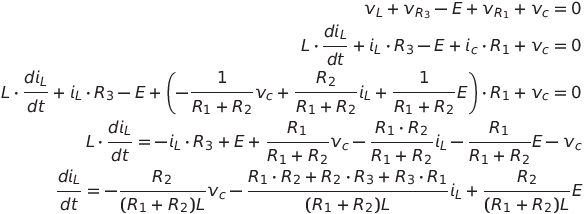
Αυτή είναι η δεύτερη σχέση.
---------------------------------------
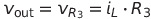
---------------------------------------
Τελικά έχεις:
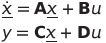
με:
Οι εξισώσεις κατάστασης. :)
Ε, την συνάρτηση μεταφοράς την βγάζεις με τον γνωστό τύπο:
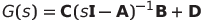
Αυτά, ελπίζω να μην έφυγε κάνα πρόσημο!! :P
Τα ΣΑΕ γενικά κάνουν τα μυαλά να πονάνε! :D :D :D :D
Για το θέμα 1ο αρχικά διαλέγεις ένα διάνυσμα κατάστασης. Αν θυμάσαι απ' τα Κυκλώματα, ένα εύκολο διάνυσμα κατάστασης - και σίγουρο - είναι οι τάσεις των πυκνωτών και τα ρεύματα των πηνίων.
Δηλαδή:
Εδώ έχεις μικρό κυκλωματάκι, οπότε μπορείς να πας λίγο στα.. τυφλά. Πάνω-κάτω να θυμάσαι ότι πρέπει να κάνεις τουλάχιστον ένα νόμο τάσεων για την τάση του πηνίου κι ένα νόμο ρευμάτων για το ρεύμα του πηνίου (πάνε "ανάποδα" θα δεις γιατί). Για μεγαλύτερα κυκλώματα, υπάρχει πιο συστηματική μέθοδος και είναι στο κεφάλαιο των εξισώσεων κατάστασης του Β' τόμου των Κυκλωμάτων: επίλυση με γράφους. Τα λέει αρκετά καλά. ;)
Έχεις:
---------------------------------------
1)ΝΡΚ:
Όμως:
Αντικαθιστώντας:
Αυτή είναι η πρώτη σχέση.
---------------------------------------
2)ΝΤΚ:
Αυτή είναι η δεύτερη σχέση.
---------------------------------------
---------------------------------------
Τελικά έχεις:
με:
Οι εξισώσεις κατάστασης. :)
Ε, την συνάρτηση μεταφοράς την βγάζεις με τον γνωστό τύπο:
Αυτά, ελπίζω να μην έφυγε κάνα πρόσημο!! :P
Τα ΣΑΕ γενικά κάνουν τα μυαλά να πονάνε! :D :D :D :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sakaflias7 on February 07, 2009, 03:34:03 am
θνξ ρε george αλλά την H(s) ψάχνω με τον τρόπο δι'απαλοιφής
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: crystal on February 07, 2009, 14:25:37 pm
Απο του 2000 στο 2ο, το ωc προσεγγιστικα κανεις?? :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Γιώργος on February 07, 2009, 16:41:08 pm
8nx re george alla thn H(s) psaxnw me ton tropo di'apaloifhs...
Ποια μέθοδος είναι αυτή; :o
Αν την θες κατευθείαν μπορείς να το λύσεις σαν άσκηση κυκλωμάτων στο πεδίο της μιγαδικής συχνότητας.
-----------------------------------------
Αρχικά, διαιρέτης τάσης και βρίσκεις την
όπου
Από 2ο διαιρέτη:
Αντικαθιστάς
ps: σε όλα τα παραπάνω επιφυλάσσομαι για τυχόν λάθη, οπότε μην τα δέσετε και κόμπο. :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kargas on August 25, 2010, 19:01:50 pm
to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Λεπόν βρήκα ένα παλιό θέμα του 99 σε ένα υποερώτημα φάση να λέει να κάνεις το γτρ του -6/(s+3)(s+6)
το πέταξα στο matlab και έβγαλε τους 2 πόλους να πηγαίνουν ο -3 στο +οο και ο -6 στο -οο, γτ γίνεται αυτό;wtf;;; αν ήταν 6/(s+3)(s+6) οι δύο πόλοι χτυπιούνται και φεύγουν προς τα πάνω κάτω στις 90 μοίρες.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 25, 2010, 20:25:38 pm
lepon brika ena palio 8ema tou 99 kai se ena upoerotima fash leei na kaneis to gtr tou -6/(s+3)(s+6)
to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Λογικά κάτι θα αλλάζει στην εξίσωση του ΓΤΡ (1 + kA(s) = 0).to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 25, 2010, 21:02:37 pm
ΘΕΜΑ 2. ΣΕΠΤΕΜΒΡΙΟΣ 2008 ΕΧΩ 2 ΜΗΔΕΝΙΚΑ ΕΝΑ ΣΤΟ -3 ΚΑΙ ΕΝΑ ΣΤΟ -10
ΠΟΛΟΥΣ ΕΝΑ ΣΤΟ 0 , ΕΝΑ ΣΤΟ -2 ΕΝΑ ΣΤΟ -4 ,ΕΝΑ ΣΤΟ -8+9j ΚΑΙ ΕΝΑ ΣΤΟ -9-8j
το ελυσε κανεις προσεγγιστικα γιατι στο Matlab που την βαζω μου βγαζει αλλους πολους και ιδια μηδενικα με λογικο σχημα ενω με αυτα της ασκησης δεν μου βγαινει γμτ..
ΠΟΛΟΥΣ ΕΝΑ ΣΤΟ 0 , ΕΝΑ ΣΤΟ -2 ΕΝΑ ΣΤΟ -4 ,ΕΝΑ ΣΤΟ -8+9j ΚΑΙ ΕΝΑ ΣΤΟ -9-8j
το ελυσε κανεις προσεγγιστικα γιατι στο Matlab που την βαζω μου βγαζει αλλους πολους και ιδια μηδενικα με λογικο σχημα ενω με αυτα της ασκησης δεν μου βγαινει γμτ..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kargas on August 25, 2010, 22:19:52 pm
lepon brika ena palio 8ema tou 99 kai se ena upoerotima fash leei na kaneis to gtr tou -6/(s+3)(s+6)
to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Λογικά κάτι θα αλλάζει στην εξίσωση του ΓΤΡ (1 + kA(s) = 0).to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
ε ναι αλλά τι αλλάζει; :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 26, 2010, 00:10:55 am
οποιος εχει ας ποσταρει καμια λυση απο τα θεματα 2007-2009 με μοναδαια αρνητικη αναδραση,περιορισμοι κτλ...
+ Σεπτεμβριος 2008, αν γινει με προσεγγιση κυριου πολου ειναι δεκτη η χαραξη γτρ? το ετρεξα στο προγραμματακι για γτρ με και χωρις προσεγγιση και ηταν αρκετα διαφορετικο...ετσι οπως ειναι ομως σημεια αποσχισης δεν βρισκονται λογω 5βαθμιας εξισωσης
+ Σεπτεμβριος 2008, αν γινει με προσεγγιση κυριου πολου ειναι δεκτη η χαραξη γτρ? το ετρεξα στο προγραμματακι για γτρ με και χωρις προσεγγιση και ηταν αρκετα διαφορετικο...ετσι οπως ειναι ομως σημεια αποσχισης δεν βρισκονται λογω 5βαθμιας εξισωσης
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Cthulu on August 26, 2010, 00:55:40 am
lepon brika ena palio 8ema tou 99 kai se ena upoerotima fash leei na kaneis to gtr tou -6/(s+3)(s+6)
to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Λογικά κάτι θα αλλάζει στην εξίσωση του ΓΤΡ (1 + kA(s) = 0).to peta3a sto matlab kai evgale tous 2 polous na pigenoun o -3 sto +OO kai o -6 sto -OO , gt ginete auto? wtf??
an htan 6/(s+3)(s+6) (xwris to - dld) oi dio poloi xtipiountai kai feugoun pros ta panw katw stis 90 mires...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 26, 2010, 15:54:41 pm
ιανουαριος 2010 θεμα 3
Η Α(s) profanos einai to ginomeno tvn Hk kai Hp
prodiagrafes
1)
prokyptei 36.9b<ka (1)
2)me prosegissi poloy apaleifw to triwnymo kai sti sinexia fainetai oti i proseggisi einai sosti. Ara me tin progessigi auti prepei b<4 episis σ>=1.38 => 41b+10ka / (41+10k) >=1.38 (2)
3)O GTP A(s) exei dyo asymptotes poy bgainoyn 90,gia na exei apeiro kerdos to systhma prepei to simeio tomis tou na einai arnitiko ara a<b+8 (3)
4)se dB Hyd <= -20dB =>................................................. .............=>
100 a^2 k^2 + 100k^2 >= 0.1664b^2 + 0.1664 (4)
5) Wc=sqrt (0.06(k^2 a^2 +k^2) -b^2) >= 10 (5)
gia k=10 b=2.1 a=10 ikanopoioyntai oles 1-5......
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Η Α(s) profanos einai to ginomeno tvn Hk kai Hp
prodiagrafes
1)
prokyptei 36.9b<ka (1)
2)me prosegissi poloy apaleifw to triwnymo kai sti sinexia fainetai oti i proseggisi einai sosti. Ara me tin progessigi auti prepei b<4 episis σ>=1.38 => 41b+10ka / (41+10k) >=1.38 (2)
3)O GTP A(s) exei dyo asymptotes poy bgainoyn 90,gia na exei apeiro kerdos to systhma prepei to simeio tomis tou na einai arnitiko ara a<b+8 (3)
4)se dB Hyd <= -20dB =>................................................. .............=>
100 a^2 k^2 + 100k^2 >= 0.1664b^2 + 0.1664 (4)
5) Wc=sqrt (0.06(k^2 a^2 +k^2) -b^2) >= 10 (5)
gia k=10 b=2.1 a=10 ikanopoioyntai oles 1-5......
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 26, 2010, 17:23:14 pm
μια ενσταση σ'αυτα που κανεις..
στα θεματα ιανουριου 2010 στο (4) μου βγηκε σωστο το πρωτο σκελος της ανισωσης ενω το δευτερο μου βγηκε πολ/μενο με 1.000.000:P
παιζει να εχεις κανει λαθος η εγω?? :P
επισης στο (5) πως την βγαζεις την σχεση για το Wc??
στα θεματα ιανουριου 2010 στο (4) μου βγηκε σωστο το πρωτο σκελος της ανισωσης ενω το δευτερο μου βγηκε πολ/μενο με 1.000.000:P
παιζει να εχεις κανει λαθος η εγω?? :P
επισης στο (5) πως την βγαζεις την σχεση για το Wc??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 26, 2010, 22:46:18 pm
φιλε στο 2010 πηρα Hyd<=0.1 => | A(jω) | >=1 για ω=1 σελιδα 374. Αυτα που λενε σε διαφορα τοπικ με προσεγγισεις δεν τα καταλαβα....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
Ptixiaki 2010
1) me kathe epifilaksi...
a) Kanw ton GTP ths A(s)=k / (s+4) ^2 * (s+4)
b) proseggisi kyriou polou s+4,sbinw to s diladi kai gia na brw rizes pairnw 1+A(s)=0
bgainoun s= -2 +- 0.5*j*sqrt(k)
x=-2 y=+- 0.5*j*sqrt(k) x^2 + y^2 =4+0.25k kyklos kentro 0 aktina R=sqrt(4+0.25k)
c) Hk(s)= k / (s^2+4s+ (16+k)/4 ) tin efera stin morfi deuteras taksis....h diakrinousa tou paronomasti einai arnitiki ara apo tin antistoixia h geniki diakrinousa einai Δ=4wn^2( ζ^2-1) < 0 => -1<ζ<1 επειδη το ζ ειναι θετικο ζmin=0....
2) pairnw analogiko elegkti k
a) ess<=0.2 =>..... k>=16
b)apo to xaraktiristiko polywnymo σ=7 >=5.94 ισχυει για καθε k...
c)apo routh gia tin A(s) to sistima einai eystathes kai apeiro kerdos gia kathe k
d) thetw k=20 | A(jω) | =1 => wc=12.1 r/s θm=180 + gwnia(A(jwc))=57.86>30 tin gwnia me antikatastash toy wc stin A,migadikoi klp telika k=20...
3)a) to Bode kerdous bgainei mono me eytheies opos a4....
b)me ta idia kritiria briskw tin sinartisi metaforas H(s)=2(s+1)(0.5s+1) / (2s+1)(0.1s+1) ara a=2 b=0 kai θm=180-30=160 30 h gwnia toy wc (midenismoy bode kerdoys) kai h gwnia toy wf dhladh tis sixnothtas poy h fash ginetai -180 exei bode kerdoys katw apo 0 dB afoy to bode kerdoys synexizeis pros ta katw...ara Gm>1. Akribws den to ypologizw efoson zitaei ypologismo grafika....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
Ptixiaki 2010
1) me kathe epifilaksi...
a) Kanw ton GTP ths A(s)=k / (s+4) ^2 * (s+4)
b) proseggisi kyriou polou s+4,sbinw to s diladi kai gia na brw rizes pairnw 1+A(s)=0
bgainoun s= -2 +- 0.5*j*sqrt(k)
x=-2 y=+- 0.5*j*sqrt(k) x^2 + y^2 =4+0.25k kyklos kentro 0 aktina R=sqrt(4+0.25k)
c) Hk(s)= k / (s^2+4s+ (16+k)/4 ) tin efera stin morfi deuteras taksis....h diakrinousa tou paronomasti einai arnitiki ara apo tin antistoixia h geniki diakrinousa einai Δ=4wn^2( ζ^2-1) < 0 => -1<ζ<1 επειδη το ζ ειναι θετικο ζmin=0....
2) pairnw analogiko elegkti k
a) ess<=0.2 =>..... k>=16
b)apo to xaraktiristiko polywnymo σ=7 >=5.94 ισχυει για καθε k...
c)apo routh gia tin A(s) to sistima einai eystathes kai apeiro kerdos gia kathe k
d) thetw k=20 | A(jω) | =1 => wc=12.1 r/s θm=180 + gwnia(A(jwc))=57.86>30 tin gwnia me antikatastash toy wc stin A,migadikoi klp telika k=20...
3)a) to Bode kerdous bgainei mono me eytheies opos a4....
b)me ta idia kritiria briskw tin sinartisi metaforas H(s)=2(s+1)(0.5s+1) / (2s+1)(0.1s+1) ara a=2 b=0 kai θm=180-30=160 30 h gwnia toy wc (midenismoy bode kerdoys) kai h gwnia toy wf dhladh tis sixnothtas poy h fash ginetai -180 exei bode kerdoys katw apo 0 dB afoy to bode kerdoys synexizeis pros ta katw...ara Gm>1. Akribws den to ypologizw efoson zitaei ypologismo grafika....
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ^^DaRk_HunTeR on August 27, 2010, 04:59:47 am
Σορρυ που θα στο πω ρε συ gate4 αλλα κανεις οτι σου κατεβει στο κεφαλι...
Κανεις προσεγγιση κυριου πολου χωρις λογο σε λαθος πολο...
η Συναρτηση μεταφορας στο θεμα 3 της Πτυχιακης 2010 βγαινει για α=β=2.5 checkare τη και στο Ματλαμπ...
γενικα αυτα που γραφεις μπαζουν απο παντου... μεχρι και απο το λαθος αποτελεσμα που εβγαλες για τα α και β βγαζεις λαθος gm kai θm...
Απο αυριο-με8αυριο που θα αρχισω να λυνω σοβαρα θεματα θα επανελθω με περισσοτερες λεπτομερειες
(μεχρι τοτε ψαξου και στα προηγουμενα).
Tsimpa stis fwtoz to apotelesma mou kai to diko sou sto Matlab...
Κανεις προσεγγιση κυριου πολου χωρις λογο σε λαθος πολο...
η Συναρτηση μεταφορας στο θεμα 3 της Πτυχιακης 2010 βγαινει για α=β=2.5 checkare τη και στο Ματλαμπ...
γενικα αυτα που γραφεις μπαζουν απο παντου... μεχρι και απο το λαθος αποτελεσμα που εβγαλες για τα α και β βγαζεις λαθος gm kai θm...
Απο αυριο-με8αυριο που θα αρχισω να λυνω σοβαρα θεματα θα επανελθω με περισσοτερες λεπτομερειες
(μεχρι τοτε ψαξου και στα προηγουμενα).
Tsimpa stis fwtoz to apotelesma mou kai to diko sou sto Matlab...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 27, 2010, 07:17:31 am
λογω απροσεξιας κατασκευασα μονος την Η(s) σαν να μην ηταν δοσμενη και μετα εκανα αντιστοιχια.. οντως τοσο βγαινουν αφου κανει σε db την H(s) του ερωτηματος Α....
http://csserver.evansville.edu/~richardson/cgi-bin/bode.cgi
H(s)= 10*((s+1)*(s+2)) / ((s+0.5)*(s+2)*(s+10))
περιθωρια κερδους-φασης δεν γινεται να ειναι λαθος γιατι τα bode ειναι δοσμενα και τα βρηκα απο την θεωρια.....
η προσεγγιση στο 1 πως ειναι σωστη :???: ειναι k / (s+2)(s+2)(s+4) φευγει το 4. Αυτο το ερωτημα λυνεται μονο απο το 1+Α(s)=0 και χωρις προσεγγιση βγαινει τριτοβαθμια εξισωση με παραμετρο που ειναι λιγο δυσκολη...
http://csserver.evansville.edu/~richardson/cgi-bin/bode.cgi
H(s)= 10*((s+1)*(s+2)) / ((s+0.5)*(s+2)*(s+10))
περιθωρια κερδους-φασης δεν γινεται να ειναι λαθος γιατι τα bode ειναι δοσμενα και τα βρηκα απο την θεωρια.....
η προσεγγιση στο 1 πως ειναι σωστη :???: ειναι k / (s+2)(s+2)(s+4) φευγει το 4. Αυτο το ερωτημα λυνεται μονο απο το 1+Α(s)=0 και χωρις προσεγγιση βγαινει τριτοβαθμια εξισωση με παραμετρο που ειναι λιγο δυσκολη...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 27, 2010, 18:45:39 pm
φιλε στο 2010 πηρα Hyd<=0.1 => | A(jω) | >=1 για ω=1 σελιδα 374. Αυτα που λενε σε διαφορα τοπικ με προσεγγισεις δεν τα καταλαβα....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
ναι το καταλαβα για το πρωτο απλα σου λεω δε βρηκα το ιδιο με σενα..
επισης η προσεγγιση ειναι οτι γενικα |Hyd(jw)|<=0,1 => |1+A(jw)|>=10 και εμεις παιρνουμε |A(jw)|>=10..αυτο το κανουν γενικα ολοι στις ασκησεις αλλα ειναι σωστο?δλδ ο πετριδης δε το θεωρει λαθος αυτο?δε θελει να το λυσεις χωρις αυτην την προσεγγιση?ξερει κανεις?
οσον αφορα το δευτερο ελυσες το |A(jWc)|=1 και βρηκες μια σχεση για το Wc συναρτηση των Κ,α,b και εφτιαξες την ανισωση Wc>=10 ?
μπορω να αντικαταστησω στην |A(jWc)| το Wc=10 που μου δινει και να βρω λυση της ανισωσης |A(jWc)|<=1 ??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 27, 2010, 19:11:13 pm
φιλε στο 2010 πηρα Hyd<=0.1 => | A(jω) | >=1 για ω=1 σελιδα 374. Αυτα που λενε σε διαφορα τοπικ με προσεγγισεις δεν τα καταλαβα....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
στο αλλο απλα wc=wb (euros zwnhs) kai |A(jw)|=1. Me logA(jw) midenizetai to bode kerdous kai briskeis wc.....
ναι το καταλαβα για το πρωτο απλα σου λεω δε βρηκα το ιδιο με σενα..
επισης η προσεγγιση ειναι οτι γενικα |Hyd(jw)|<=0,1 => |1+A(jw)|>=10 και εμεις παιρνουμε |A(jw)|>=10..αυτο το κανουν γενικα ολοι στις ασκησεις αλλα ειναι σωστο?δλδ ο πετριδης δε το θεωρει λαθος αυτο?δε θελει να το λυσεις χωρις αυτην την προσεγγιση?ξερει κανεις?
οσον αφορα το δευτερο ελυσες το |A(jWc)|=1 και βρηκες μια σχεση για το Wc συναρτηση των Κ,α,b και εφτιαξες την ανισωση Wc>=10 ?
μπορω να αντικαταστησω στην |A(jWc)| το Wc=10 που μου δινει και να βρω λυση της ανισωσης |A(jWc)|<=1 ??
|Hyd(jw)|<=0,1 το 0,1 << 1 και το ω=1 ειναι ειναι πολυ χαμηλη συχνοτητα αρα απο 8.3.11 για w=1 Α(jw)>>1
Εγω πηρα Α(jw)>1 αλλα μπορεις να παρεις και αυτο που ειπες εσυ μιας και το 1 δεν επηρεαζει το αποτελεσμα,μπορεις να το αφησεις και οπως ειναι μιας και δεν προκειται να καταληξεις σε απλη ανισωση λογω 2 παραμετρων και τετραγωνων...Στο αλλο βρισκεις το wc και βαζεις wc>=10
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Anyparktos on August 27, 2010, 21:16:15 pm
Για το εύρος ζώνης γενικά παίρνεις τη συχνότητα μηδενισμού του Bode δηλαδη την ωc ίση με την τιμή που σου δίνει για εύρος ζώνης γιατί γενικά ισχύει ωc<ωb.Οπότε όταν πχ σου λέει εύρος ζώνης τουλάχιστον 10 τότε αν πάρεις το ωc=10 τότε είσαι σίγουρος ότι το ωb δλδ το εύρος ζώνης θα είναι μεγαλύτερο.Για το |Α(jωc)|=1 όπως λέτε και πιο πάνω.
Λοιπόν,αν ακολουθήσει το περσινο μοτιβο θα βαλει το 1ο θεμα φετος ιδιο με της πτυχιακης του ιουλη 2010.Το θεμα ειναι...το είδατε το θέμα 1 της πτυχιακής του Ιούλη??Μη μοναδιαία ανάδραση και ζητάει ΓΤΡ,απόδειξη ότι σε μιγαδικες ρίζες ο ΓΤΡ είναι κύκλος και μικρότερη δυνατή τιμή του ζ...Δεν καταλαβαινω!Άντε για το ΓΤΡ,θα πάρουμε ως Α(s) το γινόμενο του συστήματος επί τον ελεγκτή,ακόμα κι αν είναι στην ανάδραση(έτσι πιστεύω,αν διαφωνείτε πείτε μου).Για την απόδειξη στο β) ερώτημα δεν εχω ΙΔΕΑ και για το γ)...Ποια είναι η προϋπόθεση για να πάρει το ζ ελάχιστη τιμή?Κανείς?
EDIT:
@Vicariously,I
Για τη διαταραχή πάντως η προσέγγιση |1+Α(jω)|>=10 σε |Α(jω)|>=10 στο Α4 στις λυμένες ασκήσεις που λογικά είναι από το μάθημα την παίρνει αυτή την προσέγγιση και αν θυμάμαι καλά το είδα και στο βιβλίο ή καποιος μου πε οτι το δε.Αν σκεφτείς οτι ειναι σχεδιαση κιολας οποτε οι τιμές είναι λίγο ρευστές γιατί να μην το δεχτεί?Μπορείς να λύσεις ένα θέμα σχεδίασης και μετά αφού βάλεις νούμερα να δεις αν επαληθεύονται οι προδιαγραφές.
Λοιπόν,αν ακολουθήσει το περσινο μοτιβο θα βαλει το 1ο θεμα φετος ιδιο με της πτυχιακης του ιουλη 2010.Το θεμα ειναι...το είδατε το θέμα 1 της πτυχιακής του Ιούλη??Μη μοναδιαία ανάδραση και ζητάει ΓΤΡ,απόδειξη ότι σε μιγαδικες ρίζες ο ΓΤΡ είναι κύκλος και μικρότερη δυνατή τιμή του ζ...Δεν καταλαβαινω!Άντε για το ΓΤΡ,θα πάρουμε ως Α(s) το γινόμενο του συστήματος επί τον ελεγκτή,ακόμα κι αν είναι στην ανάδραση(έτσι πιστεύω,αν διαφωνείτε πείτε μου).Για την απόδειξη στο β) ερώτημα δεν εχω ΙΔΕΑ και για το γ)...Ποια είναι η προϋπόθεση για να πάρει το ζ ελάχιστη τιμή?Κανείς?
EDIT:
@Vicariously,I
Για τη διαταραχή πάντως η προσέγγιση |1+Α(jω)|>=10 σε |Α(jω)|>=10 στο Α4 στις λυμένες ασκήσεις που λογικά είναι από το μάθημα την παίρνει αυτή την προσέγγιση και αν θυμάμαι καλά το είδα και στο βιβλίο ή καποιος μου πε οτι το δε.Αν σκεφτείς οτι ειναι σχεδιαση κιολας οποτε οι τιμές είναι λίγο ρευστές γιατί να μην το δεχτεί?Μπορείς να λύσεις ένα θέμα σχεδίασης και μετά αφού βάλεις νούμερα να δεις αν επαληθεύονται οι προδιαγραφές.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 27, 2010, 22:22:22 pm
Σε αυτο το θεμα που λες: ναι η ανοιχτου βροχου ειναι αυτη που λες το γινομενο των δυο συναρτησεων..
(στη σχεδιαση του ΓΤΡ εχω ενα προβλημα καθως οταν παω να βρω τη γωνια αναχωρησης απτους πολους μου βγαινει 180 μοιρες πραγμα αδυνατον αφου ειναι κυκλος.θα επρεπε να ειναι 90 μοιρες..help οποιος μπορει)
αποδειξη οτι σε μιγαδικες ριζες ο ΓΤΡ ειναι κυκλος φανταζομαι εννοει οτι για τις διαφορες τιμες του κερδους Κ εμφανιζεται στον ΓΤΡ η μεταβολη των ριζων.Βρισκοντας τα σημεια αποσχισης με τη σχεση dA(s)/ds βλεπουμε οτι αυτα ειναι τα -2 και -6.Αρα μετα φανταζομαι θα λες εστω οτι ειναι κυκλος ακτινας 2 οποτε το σημειο -4(που ειναι και το μηδενικο) θα ειναι το κεντρο οποτε μετα θα πρεπει να βρεις την γωνια της Α(s) στο σημειο -4-2i η -4+2i και να την βρεις 0 η 180..η δεν ξερω αν χρειαζεται αυτο το τελευταιο.γενικα κατι τετοιο κανεις παντως νομιζω.
για τη μικροτερη τιμη του ζ εγω εγραψα τη συναρτηση κλειστου βροχου,πηρα τον τυπο για το ζ=α1/2sqrt(α0) και το παραγωγισα συναρτηση του Κ.
(στη σχεδιαση του ΓΤΡ εχω ενα προβλημα καθως οταν παω να βρω τη γωνια αναχωρησης απτους πολους μου βγαινει 180 μοιρες πραγμα αδυνατον αφου ειναι κυκλος.θα επρεπε να ειναι 90 μοιρες..help οποιος μπορει)
αποδειξη οτι σε μιγαδικες ριζες ο ΓΤΡ ειναι κυκλος φανταζομαι εννοει οτι για τις διαφορες τιμες του κερδους Κ εμφανιζεται στον ΓΤΡ η μεταβολη των ριζων.Βρισκοντας τα σημεια αποσχισης με τη σχεση dA(s)/ds βλεπουμε οτι αυτα ειναι τα -2 και -6.Αρα μετα φανταζομαι θα λες εστω οτι ειναι κυκλος ακτινας 2 οποτε το σημειο -4(που ειναι και το μηδενικο) θα ειναι το κεντρο οποτε μετα θα πρεπει να βρεις την γωνια της Α(s) στο σημειο -4-2i η -4+2i και να την βρεις 0 η 180..η δεν ξερω αν χρειαζεται αυτο το τελευταιο.γενικα κατι τετοιο κανεις παντως νομιζω.
για τη μικροτερη τιμη του ζ εγω εγραψα τη συναρτηση κλειστου βροχου,πηρα τον τυπο για το ζ=α1/2sqrt(α0) και το παραγωγισα συναρτηση του Κ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 27, 2010, 23:12:27 pm
o τυπος ζ=α1/2sqrt(α0) για ποια συναρτηση ειναι? εκανες προσεγγιση? στο β εγω εβγαλα τις ριζες του γτρ s=-2+-0.5sqrt(k) αφου εκανα προσεγγιση του 4 και μετα x+yi κτλ..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 27, 2010, 23:38:38 pm
επισης 2009 ιουλιος (οποιος αλλος εχει κανενα θεμα ας ποσταρει)
1) a) A(s)=k(s+5)(s+10) /s(s+2)( (s+a)^2+25) poloi 4 midenika 2 asympotetes dyo 90 kai -90 moires temontai sto 6.5-a, gia na yparxei eystatheia a>6,5
b) ts<=2.8 => σ>=1.486 otan k->oo oi pio kontinoi poloi proseggizoyn thn asymptoto sto pragmatiko meros ara 6.5-a<=-1.486 a>=7.896
a=8
c) A(s)=k(s+5)(s+10) /s(s+2)( (s+8)^2+25) shmeia aposxishs sto peripou anamesa stp -6 -10 ,kai 0 -2 apo tis alles idiotites tou gtp..
augoustos 2009
2) pairnw PI A(s)=50kp(s+c) / s(s+3)(s+10) c=ki/kp
a)ess=0
b)esr<=0.1 => kp>=6
c)Hyd<=0.1 => 2500kp^2(0.01+c^2) >=901.1
d)Huv=Hc(s) /1+A(s) kai pairnw tin teliki timis uss h opoia bgainei 0.6 <=1 ara isxyei panta
5) me routh 1+A(s) gia eystatheia...telika bgainei kp> (c-30)/50 mautin tin synthiki diladi einai eystathes ara apeiro kerdos
ola ta parapanw isxyoyn gia c=1000 kp=20....
2007 iounios
1)briskw A(s) apo tis sinartiseis h opoia einai ena makrinari......ess=0 esr=0.5
2) bode kerdous kata ta gnwsta, gia akribi perithoria oxi apo diagramma....|H(jw)|=1 => wc=7.1
meta gwnia H(jwc) opote θm=180- gwnia=84 .To perithwrio kerdous kai apo nyquist kai apo routh bgainei +oo
3) Auti i askisi exei pousti@...Den lynetai me PI, mono me P: A(s)=10k(s+6) / s(s+1)
a)ess=0
b) apo routh apeiro kerdos
c)σ>=4.16 => k>=0.732
d) |Hyd| <=1 => |A(jw)+1|>=1 ktl edw den ginetai proseggisi
(60k+1)^2+10^6k^2>=10^8+10^4 gia k=100 isxyoyn...
1) a) A(s)=k(s+5)(s+10) /s(s+2)( (s+a)^2+25) poloi 4 midenika 2 asympotetes dyo 90 kai -90 moires temontai sto 6.5-a, gia na yparxei eystatheia a>6,5
b) ts<=2.8 => σ>=1.486 otan k->oo oi pio kontinoi poloi proseggizoyn thn asymptoto sto pragmatiko meros ara 6.5-a<=-1.486 a>=7.896
a=8
c) A(s)=k(s+5)(s+10) /s(s+2)( (s+8)^2+25) shmeia aposxishs sto peripou anamesa stp -6 -10 ,kai 0 -2 apo tis alles idiotites tou gtp..
augoustos 2009
2) pairnw PI A(s)=50kp(s+c) / s(s+3)(s+10) c=ki/kp
a)ess=0
b)esr<=0.1 => kp>=6
c)Hyd<=0.1 => 2500kp^2(0.01+c^2) >=901.1
d)Huv=Hc(s) /1+A(s) kai pairnw tin teliki timis uss h opoia bgainei 0.6 <=1 ara isxyei panta
5) me routh 1+A(s) gia eystatheia...telika bgainei kp> (c-30)/50 mautin tin synthiki diladi einai eystathes ara apeiro kerdos
ola ta parapanw isxyoyn gia c=1000 kp=20....
2007 iounios
1)briskw A(s) apo tis sinartiseis h opoia einai ena makrinari......ess=0 esr=0.5
2) bode kerdous kata ta gnwsta, gia akribi perithoria oxi apo diagramma....|H(jw)|=1 => wc=7.1
meta gwnia H(jwc) opote θm=180- gwnia=84 .To perithwrio kerdous kai apo nyquist kai apo routh bgainei +oo
3) Auti i askisi exei pousti@...Den lynetai me PI, mono me P: A(s)=10k(s+6) / s(s+1)
a)ess=0
b) apo routh apeiro kerdos
c)σ>=4.16 => k>=0.732
d) |Hyd| <=1 => |A(jw)+1|>=1 ktl edw den ginetai proseggisi
(60k+1)^2+10^6k^2>=10^8+10^4 gia k=100 isxyoyn...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 28, 2010, 00:51:25 am
Απορίες
Στο 1ο θέμα Ιούλιος 2009 .
Αφού η εκφώνηση ζητάει να βρούμε συνθήκες γαι να είναι το κλειστό συστημα ευσταθές πως εμείς παίρνουμε την Α(s) μόνο και εξάγουμε από εκει ασφαλή συμπεράσματα;
Στο 3ο θέμα 2007 πως είναι δυνατόν να θελει P και να είναι ess=0???
Δες και αυτό
4) gia logous e3oikonomisis energeias , apethte h teliki timi tis isodou energopoiisis gia monadiaia bhmatiki isodo anaforas na einai to poli 1...
ti 8elei na pi... an kapios 3erei na apantisi.
Στο θεμα 2 θελει limu(t)t-->oo=lims-->0(sU(s))<=1
οπου η U(s)=Hc(s)V(s)/(1+Hc(s)Hp(s))
και V(s)=1/s απο εκφωνηση.
και βγαινει οτι η συνθηκη ικανοποιειται για ολα τα c και Kp αφου απλοποιουνται
Στο 1ο θέμα Ιούλιος 2009 .
Αφού η εκφώνηση ζητάει να βρούμε συνθήκες γαι να είναι το κλειστό συστημα ευσταθές πως εμείς παίρνουμε την Α(s) μόνο και εξάγουμε από εκει ασφαλή συμπεράσματα;
Στο 3ο θέμα 2007 πως είναι δυνατόν να θελει P και να είναι ess=0???
Δες και αυτό
4) gia logous e3oikonomisis energeias , apethte h teliki timi tis isodou energopoiisis gia monadiaia bhmatiki isodo anaforas na einai to poli 1...
ti 8elei na pi... an kapios 3erei na apantisi.
Στο θεμα 2 θελει limu(t)t-->oo=lims-->0(sU(s))<=1
οπου η U(s)=Hc(s)V(s)/(1+Hc(s)Hp(s))
και V(s)=1/s απο εκφωνηση.
και βγαινει οτι η συνθηκη ικανοποιειται για ολα τα c και Kp αφου απλοποιουνται
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ilias252 on August 28, 2010, 01:24:45 am
στο θεμα του σεπτεμβριου 08, εχεις:σ>4.16=>α>0.32. θα μπορουσες να γραψεις πως προκυπτει αυτο;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: FP on August 28, 2010, 01:59:31 am
παιδια στο 1 θεμα του σεπτεμβριου 2007,στη σχεδιαση του ΓΤΡ, πως υπολογιζουμε που θα τοποθετηθει το μηδενικο C?γενικα ποια ειναι η λογικη??Help!!!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 28, 2010, 02:01:48 am
1ο θέμα Ιούλιος 2009 apo to GTPστο 6.5-α τεμνονται οι ασυμπτωτες και επειδη ειναι καθετες o γτρ τεινει στο απειρο σαυτες.αν ηταν στο δεξι ημιεπιπεδο ο γτρ θα τις πλησιαζε και θα περνουσε στο δεξι ημιεπιπεδο που σημαινει ασταθεια...ο σκοπος ειναι να ειναι στο αριστερο ημιεπιπεδο 6.5-α<0=> α>6.5.σορυ λαθος στην αντιγραφη ...
3ο 2007 απλα παιρνεις οριο s->0 ths sE(s) και βγαινει 0.Βασικα δεν ειναι κανονας ess=0 αρα ολοκληρωτης. πρωτα πρεπει να βλεπεις για k και μετα ολοκληρωτη. Εγω πηρα κατευθειαν ολοκληρωτη επειδη ess=0 και μετα απο μιση ωρα καταλαβα οτι δεν βγαινει
σεπτεμβριου 08 παντα το ts=4.16/σ edw ts<=1 =>σ>=4.16. Και λεω παντα Εδω στο βιβλιο παιρνει αυτο τον τυπο που ειναι για δευτερας ταξης ακομα και για Α(s)=k / s+1 ;D
πτυχιαχη 2010 1 β) για να βρεθουν οι ριζες του γτρ πρεπει να λυθει 1+Α(s)=0 απο εκει και περα για αποδειχθει οτι ο γτρ ειναι κυκλος αν αντικαταστασεις s=x+yi και κανεις πραξεις δεν βγαζει πουθενα...αλλα να γινεται με αλλον τροπο δεν ξερω.
3ο 2007 απλα παιρνεις οριο s->0 ths sE(s) και βγαινει 0.Βασικα δεν ειναι κανονας ess=0 αρα ολοκληρωτης. πρωτα πρεπει να βλεπεις για k και μετα ολοκληρωτη. Εγω πηρα κατευθειαν ολοκληρωτη επειδη ess=0 και μετα απο μιση ωρα καταλαβα οτι δεν βγαινει
σεπτεμβριου 08 παντα το ts=4.16/σ edw ts<=1 =>σ>=4.16. Και λεω παντα Εδω στο βιβλιο παιρνει αυτο τον τυπο που ειναι για δευτερας ταξης ακομα και για Α(s)=k / s+1 ;D
πτυχιαχη 2010 1 β) για να βρεθουν οι ριζες του γτρ πρεπει να λυθει 1+Α(s)=0 απο εκει και περα για αποδειχθει οτι ο γτρ ειναι κυκλος αν αντικαταστασεις s=x+yi και κανεις πραξεις δεν βγαζει πουθενα...αλλα να γινεται με αλλον τροπο δεν ξερω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 28, 2010, 02:29:20 am
αλλουνου σαε ευαγγελια :P http://www.control.ece.ntua.gr/UndergraduateCourses/SAE/LimenaThemataExetaseon.pdf
σελιδα 20 εχει παρομοιο με το 1β ιουλιου πτυχιακη 2010 και το λυνει με αντικατασταση x+yi. Γιαυτο μαλλον θελει προσεγγιση πολου ...
σελιδα 20 εχει παρομοιο με το 1β ιουλιου πτυχιακη 2010 και το λυνει με αντικατασταση x+yi. Γιαυτο μαλλον θελει προσεγγιση πολου ...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 28, 2010, 02:33:49 am
3ο 2007 απλα παιρνεις οριο s->0 ths sE(s) και βγαινει 0.Βασικα δεν ειναι κανονας ess=0 αρα ολοκληρωτης. πρωτα πρεπει να βλεπεις για k και μετα ολοκληρωτη. Εγω πηρα κατευθειαν ολοκληρωτη επειδη ess=0 και μετα απο μιση ωρα καταλαβα οτι δεν βγαινει
Θα μου επιτρέψεις να συμφωνήσω μαζί σου μιας και
1+H(s) =(s^2+10s+6)/s(s+1)
1/(1+H(s)) = s(s+2)/(s^2+10s+6)
ess=lim S->0 { s(s+2)/(s^2+10s+6) } =0
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 28, 2010, 04:18:12 am
Σεπτεμβριος 2007
1) Pairnw PI (afoy dokimasw me P:k) A(s)=10kp(s+3)(s+c) / s(s+6)^2+9s c=ki/kp
prodiagrafes: a)ess=0
b) gia apeiro perithwrio kerdous pairnw routh kai fainetai oti to systhma einai eystathes gia kathe kp,c>0..
c) o xronos apokatastashs einai ts=4.16/σ=>σ>=1.04 pairnw to paranomasth ths Hk dhladh to 1+A(s) xarakthristiko polywnymo to opoio einai tritou bathmou.Sautin tin periptwsh( http://www.fme.aegean.gr/sites/default/files/SAE-Session10.pdf selida 27) epeidh xrisimopoisa oloklirwti to xarakthristiko polywnymo exei tin morfh s^3+2ζωns^2+ωn^2+a opou a mia stathera. Ara σ=ζωn=(12+10kp)/2 apo to x.polywnymo s^3+(12+10kp)s^2+(30kp+10kpc+45)s+30kpc
apo σ>=1.04 bgainei mia aniswsi pou isxyei gia kathe kp>0...ara sto systhma bazw PI kai epilegw as poume kp=1 c=1 ki=1 kai sxediazw gtp A(s)=10(s+3)(s+1) / s(s+6)^2+9s kata ta gnwsta, shmeia aposxishs sthn tyxh ktl....
2) P:k elegktis
a)ess<=0.2 => k>=2.8
b) to eyros zwnhs iso me wc |A(jwc|)=1 => 100k^2(wc^2+4)=(wc^2+49)(wc^2+100)
c)Hyd<0.2 gia w=1 isxyei A(j1)>>1 A(j1)>5=>......=> k>15.89
px k=20 apo b bgainei wc=199.64>=160
To bode opws sto a4...
1) Pairnw PI (afoy dokimasw me P:k) A(s)=10kp(s+3)(s+c) / s(s+6)^2+9s c=ki/kp
prodiagrafes: a)ess=0
b) gia apeiro perithwrio kerdous pairnw routh kai fainetai oti to systhma einai eystathes gia kathe kp,c>0..
c) o xronos apokatastashs einai ts=4.16/σ=>σ>=1.04 pairnw to paranomasth ths Hk dhladh to 1+A(s) xarakthristiko polywnymo to opoio einai tritou bathmou.Sautin tin periptwsh( http://www.fme.aegean.gr/sites/default/files/SAE-Session10.pdf selida 27) epeidh xrisimopoisa oloklirwti to xarakthristiko polywnymo exei tin morfh s^3+2ζωns^2+ωn^2+a opou a mia stathera. Ara σ=ζωn=(12+10kp)/2 apo to x.polywnymo s^3+(12+10kp)s^2+(30kp+10kpc+45)s+30kpc
apo σ>=1.04 bgainei mia aniswsi pou isxyei gia kathe kp>0...ara sto systhma bazw PI kai epilegw as poume kp=1 c=1 ki=1 kai sxediazw gtp A(s)=10(s+3)(s+1) / s(s+6)^2+9s kata ta gnwsta, shmeia aposxishs sthn tyxh ktl....
2) P:k elegktis
a)ess<=0.2 => k>=2.8
b) to eyros zwnhs iso me wc |A(jwc|)=1 => 100k^2(wc^2+4)=(wc^2+49)(wc^2+100)
c)Hyd<0.2 gia w=1 isxyei A(j1)>>1 A(j1)>5=>......=> k>15.89
px k=20 apo b bgainei wc=199.64>=160
To bode opws sto a4...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 12:27:49 pm
Ptixiaki 2010
1) me kathe epifilaksi...
a) Kanw ton GTP ths A(s)=k / (s+4) ^2 * (s+4)
b) proseggisi kyriou polou s+4,sbinw to s diladi kai gia na brw rizes pairnw 1+A(s)=0
bgainoun s= -2 +- 0.5*j*sqrt(k)
x=-2 y=+- 0.5*j*sqrt(k) x^2 + y^2 =4+0.25k kyklos kentro 0 aktina R=sqrt(4+0.25k)
c) Hk(s)= k / (s^2+4s+ (16+k)/4 ) tin efera stin morfi deuteras taksis....h diakrinousa tou paronomasti einai arnitiki ara apo tin antistoixia h geniki diakrinousa einai Δ=4wn^2( ζ^2-1) < 0 => -1<ζ<1 επειδη το ζ ειναι θετικο ζmin=0....
Δες λίγο σελ 295. Νομίζω πως
H(s)=Hc*Hp=k/(s+2)^2
Hh=s+4
A(s)= Hc*Hp*Hh =k*(s+4)/(s+2)^2 & Hk(s) =Hc*Hp/(1+Hc*Hp*Hh)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 12:41:10 pm
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πιστολέρο on August 29, 2010, 13:37:09 pm
Στη σχεδίαση οταν έχουμε ώς προδιαγραφές περιθώριο κέρδους και χρόνο αποκατάστασης τι συνθήκες χρησιμοποιούμε?
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 13:41:02 pm
Στη σχεδίαση οταν έχουμε ώς προδιαγραφές περιθώριο κέρδους και χρόνο αποκατάστασης τι συνθήκες χρησιμοποιούμε?
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
δες βιβίο σελ 186-191 & 383-390 Να ξέρεις πως ts= 4.16/σ to γιατί εξηγείται μέσα στο βιβλίο.
Τώρα για το περιθώριο κέρδους αν σου λέει πως πρέπει να είναι άπειρο , κάνεις Routh στο 1+Α(s) και φροντίσεις να είναι όλοι οι συντελεστές θετικοί ή από διάγραμμα bode και περιθώριο φάσης (δεν θυμάμαι καλά την εξήγηση , την έχει μέσα ) ή από ασύμπτωτες , αν πχ η γωνία τους σου βγει +- 90 μοίρες λες πως θα έχεις άπειρο περιθώριο μιας και δεν πρόκειται ποτέ η ΓΤΡ να φτάσει τον φανταστικό άξονα!
Ουσιαστικά το περιθώριο κέρδους είναι το πόσο μπορεί να αυξηθει το Κ και το σύστημα να παραμείνει ευσταθές ή από ποιο Κ και πέρα το σύστημα γίνεται ασταθές!
Η ευστάθεια γενικά ελέγχεται απο:
-Το κριτήριο Routh,
-γεωμετρικού τόπου ριζών (Γ.Τ.Ρ)
-Bode
-Nyquist, κ.λ.π.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: fourier on August 29, 2010, 13:44:34 pm
Όταν το σύστημα έχει ανάδραση όχι μοναδιαία, ο ΓΤΡ γίνεται στο ανοιχτού βρόχου ή στο κλειστού?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: MARIOS on August 29, 2010, 13:53:36 pm
Otan sou leei perithorio kerdous oxi apeiro mexri 3 dB as poume???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Angie_Ann on August 29, 2010, 14:10:49 pm
Otan sou leei perithorio kerdous oxi apeiro mexri 3 dB as poume???
τότε πρέπει να έχεις ήδη κάνει υπόθεση για κάποιο κ και επίσης να βρεις το κ0 (δηλαδή το κ για το οποίο το σύστημα χάνει την ευστάθεια του). Με αυτά τα δύο βρίσκεισ Gm=Κ0/Κ και αν σου βγει μέσα στα όρια τότε επέλεξες σωστά το Κ.
Για την έυρεση του οριακού Κ0 υπάρχουν 2 τρόποι.
1. Κάνεις κριτήριο Routh και βρίσκεις τα όρια του κ για να είναι ευσταθές το σύστημα. Το οριακό Κ θα είναι το Κ0
2. Στο ΓΤΠ βρίσκεις το Κ για το σημείο που τέμνεται ο φανταστικός άξονας από τον γεωμετρικό σου τόπο.
Νομίζω είναι δυνατόν να το βρεις και από Bode αλλά δεν έχω καταλάβει ακριβώς πως. (εκτός από τις περιπτώσεις που έχουμε άπερο κέρδος) Αν κάποιος ξέρει, ας μας διαφωτίσει :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: MARIOS on August 29, 2010, 14:16:03 pm
Routh sto 1+A(s) etsi???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 14:28:49 pm
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πιστολέρο on August 29, 2010, 14:49:45 pm
Στη σχεδίαση οταν έχουμε ώς προδιαγραφές περιθώριο κέρδους και χρόνο αποκατάστασης τι συνθήκες χρησιμοποιούμε?
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
δες βιβίο σελ 186-191 & 383-390 Να ξέρεις πως ts= 4.16/σ to γιατί εξηγείται μέσα στο βιβλίο.
Τώρα για το περιθώριο κέρδους αν σου λέει πως πρέπει να είναι άπειρο , κάνεις Routh στο 1+Α(s) και φροντίσεις να είναι όλοι οι συντελεστές θετικοί ή από διάγραμμα bode και περιθώριο φάσης (δεν θυμάμαι καλά την εξήγηση , την έχει μέσα ) ή από ασύμπτωτες , αν πχ η γωνία τους σου βγει +- 90 μοίρες λες πως θα έχεις άπειρο περιθώριο μιας και δεν πρόκειται ποτέ η ΓΤΡ να φτάσει τον φανταστικό άξονα!
Ουσιαστικά το περιθώριο κέρδους είναι το πόσο μπορεί να αυξηθει το Κ και το σύστημα να παραμείνει ευσταθές ή από ποιο Κ και πέρα το σύστημα γίνεται ασταθές!
Η ευστάθεια γενικά ελέγχεται απο:
-Το κριτήριο Routh,
-γεωμετρικού τόπου ριζών (Γ.Τ.Ρ)
-Bode
-Nyquist, κ.λ.π.
για το ts εννοώ το εξής:
εχω τον παρακάτω γτρ
http://yfrog.com/bhrlocusp (http://yfrog.com/bhrlocusp)
βλέπουμε οτι για k από 0 εως άπειρο ο πόλος μετακινείται από το 0 στο -2,5
εαν πρεπει ts<4 seconds δηλαδή ο πλησιέστερος στο 0 πόλος να βρίσκεται αριστερά του -1 τοτε πως βρίσκω μια κατάλληλη τιμή του k?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 14:54:52 pm
Θεμα 1 φλεβαρης 2008
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 14:55:16 pm
kkostorp gia to 1o ptixiaki 2010 einai A(s)= Hc*Hp*Hh =k*(s+4)/(s+2)^2 lythike to musthrio :D malakia ekana sto 1o giauto den ebgainan ta alla.twra afoy twra 1+A(s) triwnymo lynetai eykola
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 15:09:11 pm
kkostorp gia to 1o ptixiaki 2010 einai A(s)= Hc*Hp*Hh =k*(s+4)/(s+2)^2 lythike to musthrio :D malakia ekana sto 1o giauto den ebgainan ta alla.twra afoy twra 1+A(s) triwnymo lynetai eykola
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
Ναι αλλά δες τον τύπο 4.4.5 και το σχήμα 4.4.1 σελ 202 , 203.
Στο σφάλμα γενικά Ε(s)= V(s)/(1+H(s))
Αν V(s) = 1/s δηαδή η μοναδιαί βηματική τότε το Ε(s) είναι το σφάλμα θέσης και kp = lim s->0 (A(s))
αν'αλογα αν θέλουμε σφάλμα ταχύτητας το V(s) =1/s^2 και esr =1/(1+ Ku) όπου Κυ = limS->0 (s*H(s)) δηλαδή σε μας Η(s)
του τύπου είναι το Α(s)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 15:32:28 pm
kkostorp gia to 1o ptixiaki 2010 einai A(s)= Hc*Hp*Hh =k*(s+4)/(s+2)^2 lythike to musthrio :D malakia ekana sto 1o giauto den ebgainan ta alla.twra afoy twra 1+A(s) triwnymo lynetai eykola
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
2008 semptembrios thema 3)
1) ess<0.1 => 8a/(8a+7k)<0.1
2)σ>4.16 => a>0.32 (1) kai se syndyasmo me tin 1h k>3.29 (2)
4) 20logHyd <= 20log10 => ................... => a<=sqrt(0.0075k^2 - 1) (3)
5) Hyn<=10 => ............. => a>= sqrt(0.0075k^2 - 1) (4)
apo 4 kai 5 a=sqrt(0.0075k^2 - 1)
3) Wc=sqrt(7k) >=20
k=100 a=8,6 isxyoyn oles
Νομίζω πως έπρεπε να πάρεις ως Α(s) την Hc*Hp και ess= 1/(1+kp) όπου kp = lim s->0 (A(s)) και όχι Ηκ(s) που πήρες...
den pira Hk(s) gia sfalmata pantoy orio s->0 sE(s)
Ναι αλλά δες τον τύπο 4.4.5 και το σχήμα 4.4.1 σελ 202 , 203.
Στο σφάλμα γενικά Ε(s)= V(s)/(1+H(s))
Αν V(s) = 1/s δηαδή η μοναδιαί βηματική τότε το Ε(s) είναι το σφάλμα θέσης και kp = lim s->0 (A(s))
αν'αλογα αν θέλουμε σφάλμα ταχύτητας το V(s) =1/s^2 και esr =1/(1+ Ku) όπου Κυ = limS->0 (s*H(s)) δηλαδή σε μας Η(s)
του τύπου είναι το Α(s)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Anyparktos on August 29, 2010, 15:39:15 pm
Μια γενικη απορία για χρόνο αποκατάστασης κι όποιος κατάλαβε ας βοηθήσει.Κανονικά το ts=4,16/σ και συνηθως το ts είναι μικρότερο από μια τιμή που σημαίνει ότι το πραγματικό μερος πόλου πρέπει να είναι μεγαλύτερο από το 4,16/ts(σ>=4,16/ts δηλαδη) κι οπου ts βάζουμε την μεγιστη τιμη του.Αυτο γενικα ισχυει οταν ο παρονομαστης της συναρτησης κλειστού βρόγχου ειναι πολυωνυμο ως προς s δευτερου βαθμου.Οταν το πολυωνυμο ειναι ακόμα μεγαλύτερου βαθμου μετά τι κάνουμε?Θελουμε γενικα το πραγματικό μερος(ακόμα κι αν ο πόλος ειναι πραγματικος) να είναι μεγαλύτερο απο την τιμή που υπολογίσαμε για ΟΛΟΥΣ τους πολους της συναρτησης κλειστου βρογχου.Συνήθως δε εχουμε αγνώστους τους συντελεστές των ελεγκτών.Εγω το μονο συμπερασμα που βγαλα ειναι οτι αντικαθιστούμε σε φάση trial&error τιμες των ελεγκτών και μετά λύνουμε την εξισωση του πολυωνυμου για να δουμε αν επαληθευεται.Κι αμα ειναι μεχρι 3ου βαθμου,παλι καλα εχουμε τα κομπιουτερακια μας,αμα ειναι μεγαλυτερου τι στο πεος κανουμε?Αν έχει καποιος καταλαβει πληρως πως εφαρμοζεται το κριτηριο του χρόνου αποκατάστασης να μου πει.Ειμαι σχεδον σιγουρος οτι αναφερεται στους πολους της ΣΚΒ αλλα αν δεν ισχύει αυτό ας μου πει κάποιος.
Όταν το σύστημα έχει ανάδραση όχι μοναδιαία, ο ΓΤΡ γίνεται στο ανοιχτού βρόχου ή στο κλειστού?
Βγαλαμε νωριτερα συμπερασμα ότι ειναι στο ανοικτου βρόγχου(δλδ Α(s) για το ΓΤΡ θα ειναι η συναρτηση Hp επι αυτήν που χουμε στην αναδραση)Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 15:43:05 pm
Μια γενικη απορία για χρόνο αποκατάστασης κι όποιος κατάλαβε ας βοηθήσει.Κανονικά το ts=4,16/σ και συνηθως το ts είναι μικρότερο από μια τιμή που σημαίνει ότι το πραγματικό μερος πόλου πρέπει να είναι μεγαλύτερο από το 4,16/ts(σ>=4,16/ts δηλαδη) κι οπου ts βάζουμε την μεγιστη τιμη του.Αυτο γενικα ισχυει οταν ο παρονομαστης της συναρτησης κλειστού βρόγχου ειναι πολυωνυμο ως προς s δευτερου βαθμου.Οταν το πολυωνυμο ειναι ακόμα μεγαλύτερου βαθμου μετά τι κάνουμε?Θελουμε γενικα το πραγματικό μερος(ακόμα κι αν ο πόλος ειναι πραγματικος) να είναι μεγαλύτερο απο την τιμή που υπολογίσαμε για ΟΛΟΥΣ τους πολους της συναρτησης κλειστου βρογχου.Συνήθως δε εχουμε αγνώστους τους συντελεστές των ελεγκτών.Εγω το μονο συμπερασμα που βγαλα ειναι οτι αντικαθιστούμε σε φάση trial&error τιμες των ελεγκτών και μετά λύνουμε την εξισωση του πολυωνυμου για να δουμε αν επαληθευεται.Κι αμα ειναι μεχρι 3ου βαθμου,παλι καλα εχουμε τα κομπιουτερακια μας,αμα ειναι μεγαλυτερου τι στο πεος κανουμε?Αν έχει καποιος καταλαβει πληρως πως εφαρμοζεται το κριτηριο του χρόνου αποκατάστασης να μου πει.Ειμαι σχεδον σιγουρος οτι αναφερεται στους πολους της ΣΚΒ αλλα αν δεν ισχύει αυτό ας μου πει κάποιος.
Όταν το σύστημα έχει ανάδραση όχι μοναδιαία, ο ΓΤΡ γίνεται στο ανοιχτού βρόχου ή στο κλειστού?
Βγαλαμε νωριτερα συμπερασμα ότι ειναι στο ανοικτου βρόγχου(δλδ Α(s) για το ΓΤΡ θα ειναι η συναρτηση Hp επι αυτήν που χουμε στην αναδραση)Δες εδώ για τρίτου βαθμού
Σεπτεμβριος 2007
1) Pairnw PI (afoy dokimasw me P:k) A(s)=10kp(s+3)(s+c) / s(s+6)^2+9s c=ki/kp
prodiagrafes: a)ess=0
b) gia apeiro perithwrio kerdous pairnw routh kai fainetai oti to systhma einai eystathes gia kathe kp,c>0..
c) o xronos apokatastashs einai ts=4.16/σ=>σ>=1.04 pairnw to paranomasth ths Hk dhladh to 1+A(s) xarakthristiko polywnymo to opoio einai tritou bathmou.Sautin tin periptwsh( http://www.fme.aegean.gr/sites/default/files/SAE-Session10.pdf selida 27) epeidh xrisimopoisa oloklirwti to xarakthristiko polywnymo exei tin morfh s^3+2ζωns^2+ωn^2+a opou a mia stathera. Ara σ=ζωn=(12+10kp)/2 apo to x.polywnymo s^3+(12+10kp)s^2+(30kp+10kpc+45)s+30kpc
apo σ>=1.04 bgainei mia aniswsi pou isxyei gia kathe kp>0...ara sto systhma bazw PI kai epilegw as poume kp=1 c=1 ki=1 kai sxediazw gtp A(s)=10(s+3)(s+1) / s(s+6)^2+9s kata ta gnwsta, shmeia aposxishs sthn tyxh ktl....
2) P:k elegktis
a)ess<=0.2 => k>=2.8
b) to eyros zwnhs iso me wc |A(jwc|)=1 => 100k^2(wc^2+4)=(wc^2+49)(wc^2+100)
c)Hyd<0.2 gia w=1 isxyei A(j1)>>1 A(j1)>5=>......=> k>15.89
px k=20 apo b bgainei wc=199.64>=160
To bode opws sto a4...
1) Pairnw PI (afoy dokimasw me P:k) A(s)=10kp(s+3)(s+c) / s(s+6)^2+9s c=ki/kp
prodiagrafes: a)ess=0
b) gia apeiro perithwrio kerdous pairnw routh kai fainetai oti to systhma einai eystathes gia kathe kp,c>0..
c) o xronos apokatastashs einai ts=4.16/σ=>σ>=1.04 pairnw to paranomasth ths Hk dhladh to 1+A(s) xarakthristiko polywnymo to opoio einai tritou bathmou.Sautin tin periptwsh( http://www.fme.aegean.gr/sites/default/files/SAE-Session10.pdf selida 27) epeidh xrisimopoisa oloklirwti to xarakthristiko polywnymo exei tin morfh s^3+2ζωns^2+ωn^2+a opou a mia stathera. Ara σ=ζωn=(12+10kp)/2 apo to x.polywnymo s^3+(12+10kp)s^2+(30kp+10kpc+45)s+30kpc
apo σ>=1.04 bgainei mia aniswsi pou isxyei gia kathe kp>0...ara sto systhma bazw PI kai epilegw as poume kp=1 c=1 ki=1 kai sxediazw gtp A(s)=10(s+3)(s+1) / s(s+6)^2+9s kata ta gnwsta, shmeia aposxishs sthn tyxh ktl....
2) P:k elegktis
a)ess<=0.2 => k>=2.8
b) to eyros zwnhs iso me wc |A(jwc|)=1 => 100k^2(wc^2+4)=(wc^2+49)(wc^2+100)
c)Hyd<0.2 gia w=1 isxyei A(j1)>>1 A(j1)>5=>......=> k>15.89
px k=20 apo b bgainei wc=199.64>=160
To bode opws sto a4...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πιστολέρο on August 29, 2010, 15:49:28 pm
Στη σχεδίαση οταν έχουμε ώς προδιαγραφές περιθώριο κέρδους και χρόνο αποκατάστασης τι συνθήκες χρησιμοποιούμε?
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
Για το χρόνο αποκατάστασης ξέρουμε οτι είναι ίσος με 4,16/α οπου α ο πλησιέστερος στο μηδέν πόλος.
Μπορούμε δηλαδή να πουμε 4,16/α < ts οπότε βγάζουμε μια συνθήκη για τη θέση του πόλου. Ομως η θέση του πόλου εξαρτάται κ απο την τιμή του k. Πως θα γνωρίζουμε σε ποιες τιμές του k αντιστοιχεί η επιθυμητή θέση του πόλου?
για να καταλάβετε καλύτερα τι εννοώ --> βιβλίο ,σελ 404 (παράδειγμα)
δες βιβίο σελ 186-191 & 383-390 Να ξέρεις πως ts= 4.16/σ to γιατί εξηγείται μέσα στο βιβλίο.
Τώρα για το περιθώριο κέρδους αν σου λέει πως πρέπει να είναι άπειρο , κάνεις Routh στο 1+Α(s) και φροντίσεις να είναι όλοι οι συντελεστές θετικοί ή από διάγραμμα bode και περιθώριο φάσης (δεν θυμάμαι καλά την εξήγηση , την έχει μέσα ) ή από ασύμπτωτες , αν πχ η γωνία τους σου βγει +- 90 μοίρες λες πως θα έχεις άπειρο περιθώριο μιας και δεν πρόκειται ποτέ η ΓΤΡ να φτάσει τον φανταστικό άξονα!
Ουσιαστικά το περιθώριο κέρδους είναι το πόσο μπορεί να αυξηθει το Κ και το σύστημα να παραμείνει ευσταθές ή από ποιο Κ και πέρα το σύστημα γίνεται ασταθές!
Η ευστάθεια γενικά ελέγχεται απο:
-Το κριτήριο Routh,
-γεωμετρικού τόπου ριζών (Γ.Τ.Ρ)
-Bode
-Nyquist, κ.λ.π.
για το ts εννοώ το εξής:
εχω τον παρακάτω γτρ
http://yfrog.com/bhrlocusp (http://yfrog.com/bhrlocusp)
βλέπουμε οτι για k από 0 εως άπειρο ο πόλος μετακινείται από το 0 στο -2,5
εαν πρεπει ts<4 seconds δηλαδή ο πλησιέστερος στο 0 πόλος να βρίσκεται αριστερά του -1 τοτε πως βρίσκω μια κατάλληλη τιμή του k?
anyone?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Anyparktos on August 29, 2010, 15:54:06 pm
@kkostorp
Thanx,θα το κοιταξω απλα ειμαι σε νετ καφε και πρεπει να την κανω(κομμενο ιντερνετ μες την εξεταστικη...θανατος)
Thanx,θα το κοιταξω απλα ειμαι σε νετ καφε και πρεπει να την κανω(κομμενο ιντερνετ μες την εξεταστικη...θανατος)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 16:01:37 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 16:03:41 pm
του ιανουαριου 2010 το πρωτο θεμα με την χρονικη καθυστερηση το λυσε κανεις?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 16:13:48 pm
του ιανουαριου 2010 το πρωτο θεμα με την χρονικη καθυστερηση το λυσε κανεις?
Κανεις??Και οταν μας δινει χρονο ανοδου ποια σχεση παιρνουμε (π-θ/ωd?)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ilias252 on August 29, 2010, 16:17:59 pm
@ gate 4
νομιζω οτι στο θεμα αυγουστου 2009 εχεις λαθος στο routh.
η σχεση που βγαζω ειναι: 390 + 650kp -50kp*c >0..
νομιζω οτι στο θεμα αυγουστου 2009 εχεις λαθος στο routh.
η σχεση που βγαζω ειναι: 390 + 650kp -50kp*c >0..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 16:18:58 pm
του ιανουαριου 2010 το πρωτο θεμα με την χρονικη καθυστερηση το λυσε κανεις?
Κανεις??Και οταν μας δινει χρονο ανοδου ποια σχεση παιρνουμε (π-θ/ωd?)
https://www.thmmy.gr/smf/index.php?topic=37490.15 στη σελίδα 2
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 16:22:14 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Λοιπόν :
-Πες μου λιγάκι ποια θα είναι η μορφή του τόπου στο α
- Για το β συμφωνώ απολύτως
Ότι είχα γράψει για το γ άκυρο απλά πως βρήκε κ=2?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 16:27:18 pm
@ gate 4
νομιζω οτι στο θεμα αυγουστου 2009 εχεις λαθος στο routh.
η σχεση που βγαζω ειναι: 390 + 650kp -50kp*c >0..
swstos px gia kp=10 c=1 isxyoynνομιζω οτι στο θεμα αυγουστου 2009 εχεις λαθος στο routh.
η σχεση που βγαζω ειναι: 390 + 650kp -50kp*c >0..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 16:36:59 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Λοιπόν :
-Πες μου λιγάκι ποια θα είναι η μορφή του τόπου στο α
- Για το β συμφωνώ απολύτως
-Νομίζω πως βρήκες λάθος Κ χωρίς να δω το γ ερώτημα πρόσεξε
Δ= (4+κ)^2 -4*(4+κ) = (4+κ) * (4+κ-4) = κ*(4+κ) είναι αρνητική ΜΟΝΟ για Κ(-4,-0) τσέκαρε το
-
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 16:49:33 pm
Θεμα 1 φλεβαρης 2008
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
Και εγώ έχω μπερδευτεί
Αυτό που μπορώ με σιγουριά είναι
3 πόλοι -1, -4 , -5
1 μηδενικό -12
max(3,1) = 3 κλάδοι
3-1 = 2 ασύμπτωτες
Φ0 = 90
Φ1= 270
Σημείο τομής τους = ( -1-4-5+12)/2 = 1>0 ???????????????????
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 16:59:00 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
Λοιπόν :
-Πες μου λιγάκι ποια θα είναι η μορφή του τόπου στο α
- Για το β συμφωνώ απολύτως
Ότι είχα γράψει για το γ άκυρο απλά πως βρήκε κ=2?
anti gia to edit bale stin Hk(s) k=2 o paronomasths einai s^2+6s+12 exei migadikes rizes. To GTP balto sto programmataki genika einai oti na nai...Mantepsia kaneis pos einai i morfi tou apo ta simeia aposxishs pou bgainoun -6 -2
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: erotokritos on August 29, 2010, 17:00:46 pm
Μια γενικη απορια : αν κανουμε γεωμετρικο τοπο ριζων σε συναρτηση ανοικτου βροχου και εχει απειρο περιθωριο κερδους, αυτο σημαινει οτι και η κλειστου βροχου θα εχει επισης απειρο περιθωριο κερδουσ?
για το πρωτο θεμα φεβρουαριοσ 2008 που θα κανουμε το γτρ , στην A(s) ή για το ΣΚΒ?
για το πρωτο θεμα φεβρουαριοσ 2008 που θα κανουμε το γτρ , στην A(s) ή για το ΣΚΒ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 17:09:01 pm
Θεμα 1 φλεβαρης 2008
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
Και εγώ έχω μπερδευτεί
Αυτό που μπορώ με σιγουριά είναι
3 πόλοι -1, -4 , -5
1 μηδενικό -12
max(3,1) = 3 κλάδοι
3-1 = 2 ασύμπτωτες
Φ0 = 90
Φ1= 270
Σημείο τομής τους = ( -1-4-5+12)/2 = 1>0 ???????????????????
μετα οι αλλοι δυο σπανε στο απειρο αλλα με 90 και -90 αλλα κοβουν τον αξονα τον φανταστικο καπου για να μπορει το ΟΑ=1
το σημειο αποσχισησης ομως ειναι μανικι... εμπειρικα το βαζουμε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 17:20:00 pm
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kargas on August 29, 2010, 17:27:30 pm
Θεμα 1 φλεβαρης 2008
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
εχει κ(s+12)/(s+1)(s+4)(s+5)
o ΓΤΡ πως γινεται εδω?
Και εγώ έχω μπερδευτεί
Αυτό που μπορώ με σιγουριά είναι
3 πόλοι -1, -4 , -5
1 μηδενικό -12
max(3,1) = 3 κλάδοι
3-1 = 2 ασύμπτωτες
Φ0 = 90
Φ1= 270
Σημείο τομής τους = ( -1-4-5+12)/2 = 1>0 ???????????????????
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
gmsta giauto kopika ;D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 17:31:00 pm
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
kaneis??Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 17:35:18 pm
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
kaneis??Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Νομίζω πως ναι !
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 17:38:43 pm
οποτε τα κανω λαθος στις πραξεις
κατι αλλο οταν λεει τs<3
Μπορω να βρω απο το ΓΤΡ [Α(s)] το ΟΑ συναρτησει αγνωστων και να πω
σ=ΟΑ/2>4/ts και να βρω μια σχεση αντι να παρω την χαρακτηριστικη εξισωση 1+A(s) και να βρω το 2ζωn?
κατι αλλο οταν λεει τs<3
Μπορω να βρω απο το ΓΤΡ [Α(s)] το ΟΑ συναρτησει αγνωστων και να πω
σ=ΟΑ/2>4/ts και να βρω μια σχεση αντι να παρω την χαρακτηριστικη εξισωση 1+A(s) και να βρω το 2ζωn?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 17:40:23 pm
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
kaneis??Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Νομίζω πως ναι !
εχεις κατσει να την λυσεις μηπως?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 17:45:25 pm
Όχι αλοκληρωμένα , σε λιγάκι ίσως και θα γράψω αυτά που βρίσκω!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 17:52:15 pm
Στου Ιανουαριου τριτο θεμα 2010 που βγαινει η ΧΕ τριτοβαθμια αλλα δεν εχει απλο ολοκληρωτη στο παρανομαστη ,εχει πολο τι κανουμε
Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
kaneis??Παλι της μορφης s^3+2ζωns2+ωn^2s +A einai?
σ=ζωn?
Νομίζω πως ναι !
εχεις κατσει να την λυσεις μηπως?
file egw to ekana me proseggisi poloy,feygei to triwnyno kai brika times pou epalitheuoyn tis sinthikes...Gia tritou bathmou isxyei h morfh pou grafeis kai mallon einai pio swsta na to lyseis etsi.An elyses tin prodiagrafi 2 etsi apla bres alles times pou epalitheuoyn oles tis sinthikes
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Oltzi on August 29, 2010, 17:57:32 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Αναλυτικά το β????
Κάνω τις ίδιες πράξεις και βρίσκω (x+4)^2+y^2=4 ^idiot^
Σαν 1+A(s)=0 παίρνω το (s+2)^2+K(s+4)=0 => Κάνω αντικατάσταση x+yi => Εξισώνω το πραγματικό και το φανταστικό μέρος με το 0 => Αποτέλεσμα : (x+4)^2+y^2=4
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 18:01:23 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Αναλυτικά το β????
Κάνω τις ίδιες πράξεις και βρίσκω (x+4)^2+y^2=4 ^idiot^
Σαν A(s) παίρνω το (s+2)^2+K(s+4) => Κάνω αντικατάσταση x+yi => Εξισώνω το πραγματικό και το φανταστικό μέρος με το 0 => Αποτέλεσμα : (x+4)^2+y^2=4
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Oltzi on August 29, 2010, 18:07:45 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Αναλυτικά το β????
Κάνω τις ίδιες πράξεις και βρίσκω (x+4)^2+y^2=4 ^idiot^
Σαν A(s) παίρνω το (s+2)^2+K(s+4) => Κάνω αντικατάσταση x+yi => Εξισώνω το πραγματικό και το φανταστικό μέρος με το 0 => Αποτέλεσμα : (x+4)^2+y^2=4
Ναι ναι... Από την εξίσωση 1+Α(s)=0 προκύπτει (s+2)^2+K(s+4)=0... Αλλά πάλι το ίδιο αποτέλεσμα...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kargas on August 29, 2010, 18:18:21 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Αναλυτικά το β????
Κάνω τις ίδιες πράξεις και βρίσκω (x+4)^2+y^2=4 ^idiot^
Σαν A(s) παίρνω το (s+2)^2+K(s+4) => Κάνω αντικατάσταση x+yi => Εξισώνω το πραγματικό και το φανταστικό μέρος με το 0 => Αποτέλεσμα : (x+4)^2+y^2=4
Ναι ναι... Από την εξίσωση 1+Α(s)=0 προκύπτει (s+2)^2+K(s+4)=0... Αλλά πάλι το ίδιο αποτέλεσμα...
pfooo re gmt mporei kapoios na e3igisei ti kanoume afou vgaloume tis rizes ths XE? ti e3iswnoume me ti den katalaba
pou einai to link pou leei oti exei idia askisi?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 18:20:23 pm
epeidi paizei na mpei paromoio me 1o iouliou 2010.....
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
a gewmtrikos topos rizwn...
to b lynetai pairnontas 1+A(s)=0 kai stin synexeia akribws opws i askisi sto link,antikatastasi x+yi,pragmatiko fantastiko meros iso me to 0,apaloifh to k kai bgainei (x+1)^2+y^2=1 R=1 kentro -1,0
sto c briskw Hk= k/ s^2+(4+k)s+4+4k o paronomasths einai deyteras takshs(h morfh pou leei sto biblio) ara σ=(4+k)/2=ζsqrt(4+4k) lynw ws pros ζ, paragwgizw to z ws pros k kai bgainei oti exei elaxisto sto 2. αντικατασταση ζmin=0.866
edit to opoio einai kai logiko giati i diakrinousa toy paronomasth einai D=k^2-8k kai gia k=2 einai arnhtikh ara oi rizes tou paronomasths einai migadikoi to opoio simbenei gia mono για ζ<1 σελιδα 187...
Αναλυτικά το β????
Κάνω τις ίδιες πράξεις και βρίσκω (x+4)^2+y^2=4 ^idiot^
Σαν A(s) παίρνω το (s+2)^2+K(s+4) => Κάνω αντικατάσταση x+yi => Εξισώνω το πραγματικό και το φανταστικό μέρος με το 0 => Αποτέλεσμα : (x+4)^2+y^2=4
Ναι ναι... Από την εξίσωση 1+Α(s)=0 προκύπτει (s+2)^2+K(s+4)=0... Αλλά πάλι το ίδιο αποτέλεσμα...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Oltzi on August 29, 2010, 18:23:47 pm
pfooo re gmt mporei kapoios na e3igisei ti kanoume afou vgaloume tis rizes ths XE? ti e3iswnoume me ti den katalaba
pou einai to link pou leei oti exei idia askisi?
https://www.thmmy.gr/smf/index.php?topic=1919.msg743656#msg743656
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 18:26:44 pm
@ Kargas
Βάζει στην ΧΕ : 1+A(s) = 0 όπου S to x+yi
κάνεις πράξεις και έχεις
Re {1+A(x+yi) } + i *Im {1+A(x+yi)} =0
Άρα
Re {1+A(x+yi) } =0 και
Im {1+A(x+yi)} = 0
Σε αυτό το σύστημα έχει μόνο χ,y και κ
κάνεις απαλοιφή του Κ δηλαδή , λύνεις μία από τις 2 ως προς κ και το αντικαθιστάς στην άλλη
και ετσι μετά την αντακατάσταση έχει μία σχέση με χ κι y μόνο που είναι ίση με το 0
εκεί παίζεις λιγάκι με πράξεις παραγοντποιήσεις ή ότι άλλο σου ταιριάζει και βγαίνει η εξίσωση κύκλου.
Βάζει στην ΧΕ : 1+A(s) = 0 όπου S to x+yi
κάνεις πράξεις και έχεις
Re {1+A(x+yi) } + i *Im {1+A(x+yi)} =0
Άρα
Re {1+A(x+yi) } =0 και
Im {1+A(x+yi)} = 0
Σε αυτό το σύστημα έχει μόνο χ,y και κ
κάνεις απαλοιφή του Κ δηλαδή , λύνεις μία από τις 2 ως προς κ και το αντικαθιστάς στην άλλη
και ετσι μετά την αντακατάσταση έχει μία σχέση με χ κι y μόνο που είναι ίση με το 0
εκεί παίζεις λιγάκι με πράξεις παραγοντποιήσεις ή ότι άλλο σου ταιριάζει και βγαίνει η εξίσωση κύκλου.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 18:42:55 pm
Στο 2ο θέμα πτυχιακή 2010
από την 1η προδιαγραφή κ>16
και δεν κάνω πουθενά αντικατάσταση
2η και 3η ισχύουν γαι κάθε κ
κι στην 4η κ<=66
και επιλέγω κ=60
Υπάρχει κανείς που έβγαλε κάτι πολύ πιο διαφιρετικό που να ακυρώνει το δικό μου?
Επίσης στο 3ο θέμα στο β ερώτημα α=β=2,5 σωστά?
από την 1η προδιαγραφή κ>16
και δεν κάνω πουθενά αντικατάσταση
2η και 3η ισχύουν γαι κάθε κ
κι στην 4η κ<=66
και επιλέγω κ=60
Υπάρχει κανείς που έβγαλε κάτι πολύ πιο διαφιρετικό που να ακυρώνει το δικό μου?
Επίσης στο 3ο θέμα στο β ερώτημα α=β=2,5 σωστά?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: erotokritos on August 29, 2010, 18:48:32 pm
επειδή έχω μπερδευτεί μια ερώτηση και όποιος μπορεί ας βοηθήσει ...
Όταν έχουμε σύστημα κλειστού βρόχου με μοναδιαία αρνητική ανάδραση και η συνάρτηση ανοικτού βρόχου είναι η Α(S) και μας ζητάει να κάνουμε το γεωμετρικό τόπο ριζών , εμείς τι κάνουμε?
θα κάνουμε το γτρ της Α(S) ή του συστήματος κλειστού βρόχου!!!
Όταν έχουμε σύστημα κλειστού βρόχου με μοναδιαία αρνητική ανάδραση και η συνάρτηση ανοικτού βρόχου είναι η Α(S) και μας ζητάει να κάνουμε το γεωμετρικό τόπο ριζών , εμείς τι κάνουμε?
θα κάνουμε το γτρ της Α(S) ή του συστήματος κλειστού βρόχου!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 18:52:52 pm
στις ασκησεις με σχεδιαση επειδη στο βιβλιο τα λυνει με βαση τις γραφικες παραστασεις του matlab ^banghead^ απο α4 και θεματα
mono elegktes P kai PI xrisimopoioume..otan zitaei ess< apo kati tote pairnw k kai otan ess=0 tote pithanon PI alla prwta elegxw me k. Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...An leei xronos anodou< apo kati opws ioylios 2009 tote pairnw ts<td<apo kati giati den yparxei typos gia ton xrono anodou...Aporipsi diataraxwn to poly tosa db simainei 20log|Hyd|<=20log(tosa db) kai gia aporipsh thoryvoy to idio kai isxyoyn oi proseggiseis analoga an einai mikri sixnotita se aporipsi diataraxwn kai ypsili se aporipsi thoryvou..Eyros zwnhs toulaxiston toso..tote pairnw euros zwnhs=wc, to wc bgainei apo |A(jwc)|=1.To perithwrio fasis brisketai afou prwta antikatastisw to wc sto A(jw) kai to ferw se poliki morfi kai meta θm=180+gwnia, gwnia na einai arnitiki...Perithwrio kerdous toulaxiston toso simainei oti arkei na apodeiksw oti einai apeiro apo to routh..an leei mikrotero apo mia timi tote apo routh briskw to ko(simeio tomhs tou GTP me ton fantastiko aksona) kai apo Gm=ko/kerdos<apo kati briskw mia sinthiki.To kerdos mporei na einai to k sketo alla mporei kai px 10k h kati allo..sintelestis epi k diladi. Afou brw sinthikes epilegw stin tixi times parametrwn pou ikanopoioun oles tis sinthikes.. Psilostandar auta kathe xrono peripou ta idia einai..
mono elegktes P kai PI xrisimopoioume..otan zitaei ess< apo kati tote pairnw k kai otan ess=0 tote pithanon PI alla prwta elegxw me k. Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...An leei xronos anodou< apo kati opws ioylios 2009 tote pairnw ts<td<apo kati giati den yparxei typos gia ton xrono anodou...Aporipsi diataraxwn to poly tosa db simainei 20log|Hyd|<=20log(tosa db) kai gia aporipsh thoryvoy to idio kai isxyoyn oi proseggiseis analoga an einai mikri sixnotita se aporipsi diataraxwn kai ypsili se aporipsi thoryvou..Eyros zwnhs toulaxiston toso..tote pairnw euros zwnhs=wc, to wc bgainei apo |A(jwc)|=1.To perithwrio fasis brisketai afou prwta antikatastisw to wc sto A(jw) kai to ferw se poliki morfi kai meta θm=180+gwnia, gwnia na einai arnitiki...Perithwrio kerdous toulaxiston toso simainei oti arkei na apodeiksw oti einai apeiro apo to routh..an leei mikrotero apo mia timi tote apo routh briskw to ko(simeio tomhs tou GTP me ton fantastiko aksona) kai apo Gm=ko/kerdos<apo kati briskw mia sinthiki.To kerdos mporei na einai to k sketo alla mporei kai px 10k h kati allo..sintelestis epi k diladi. Afou brw sinthikes epilegw stin tixi times parametrwn pou ikanopoioun oles tis sinthikes.. Psilostandar auta kathe xrono peripou ta idia einai..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 18:57:51 pm
επειδή έχω μπερδευτεί μια ερώτηση και όποιος μπορεί ας βοηθήσει ...
Όταν έχουμε σύστημα κλειστού βρόχου με μοναδιαία αρνητική ανάδραση και η συνάρτηση ανοικτού βρόχου είναι η Α(S) και μας ζητάει να κάνουμε το γεωμετρικό τόπο ριζών , εμείς τι κάνουμε?
θα κάνουμε το γτρ της Α(S) ή του συστήματος κλειστού βρόχου!!!
Όταν έχουμε σύστημα κλειστού βρόχου με μοναδιαία αρνητική ανάδραση και η συνάρτηση ανοικτού βρόχου είναι η Α(S) και μας ζητάει να κάνουμε το γεωμετρικό τόπο ριζών , εμείς τι κάνουμε?
θα κάνουμε το γτρ της Α(S) ή του συστήματος κλειστού βρόχου!!!
Κοία επειδή κι εγώ είχα αυτή την απορία θα σου πω την απάντηση που πήρα και την επιβεβαιώσα από τις λύσεις των ασκήσεων.
Όλη η ανάλυση γίνεται για την Α(s) ουσιαστικά αυτή η ανάλυση είναι για να προσεγγίσουμε την μορφή του ΓΤΡ του κλειστού συστήματος . Βέβαια ίσως να έχεις μπερδευτεί επιδή σε μία σχεδιάση ΓΤΡ βλέπεις σε λύσεις και το Α(s) αλλά και το 1+Α(s)
Πρόσεξε:
Πόλους και ρίζες από Α(s)
To ίδιο και αύμπτωτες.
Routh όμως κάνεις μόνο στο 1+Α(s)
Δηλαδή στην ίδια άσκηση αν θες στο ΓΤΡ να δεις περιθώριο κέρδους κλπ θα κάνεις Routh στο 1+A(s)
Επίσης αν θες να βρεις σημείο τομής με τον φανταστικό άξονα στην 1+A(s)=0 Βάζεις όπου s to Jω και λύνεις. Αν βρεις αποδεκτή λύση σημαίνει πως τέμνει τον φανταστικό άξονα αλλιώς δεν τον τέμνει!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 29, 2010, 18:58:37 pm
Μια γενικη απορια : αν κανουμε γεωμετρικο τοπο ριζων σε συναρτηση ανοικτου βροχου και εχει απειρο περιθωριο κερδους, αυτο σημαινει οτι και η κλειστου βροχου θα εχει επισης απειρο περιθωριο κερδουσ?
για το πρωτο θεμα φεβρουαριοσ 2008 που θα κανουμε το γτρ , στην A(s) ή για το ΣΚΒ?
Ο ΓΤΡ έχει νόημα στο ΣΚΒ. Θεωρητικά μπορείς να μιλήσεις για ΓΤΡ σε ΣΑΒ αλλά αυτός είναι στους πόλους της A(s) and that's it. Δηλαδή δεν είναι και τόσο "τόπος" όσο σημεια :Pγια το πρωτο θεμα φεβρουαριοσ 2008 που θα κανουμε το γτρ , στην A(s) ή για το ΣΚΒ?
Για λόγους ευκολίας, αντί κάθε φορά να παίρνεις kA(s)/(1 + kA(s)) και να προσπαθείς μαθηματικά να βγάλεις το ΓΤΡ έχουν βγει οι 7 ιδιότητες που προκύπτουν αποκλειστικά από τη μορφή του A(s). Οπότε μη μπερδεύεσαι ;)
ps: απάντησε και ο gate4 ελπίζουμε πως βοηθήσαμε :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kargas on August 29, 2010, 18:59:38 pm
@ Kargas
Βάζει στην ΧΕ : 1+A(s) = 0 όπου S to x+yi
κάνεις πράξεις και έχεις
Re {1+A(x+yi) } + i *Im {1+A(x+yi)} =0
Άρα
Re {1+A(x+yi) } =0 και
Im {1+A(x+yi)} = 0
Σε αυτό το σύστημα έχει μόνο χ,y και κ
κάνεις απαλοιφή του Κ δηλαδή , λύνεις μία από τις 2 ως προς κ και το αντικαθιστάς στην άλλη
και ετσι μετά την αντακατάσταση έχει μία σχέση με χ κι y μόνο που είναι ίση με το 0
εκεί παίζεις λιγάκι με πράξεις παραγοντποιήσεις ή ότι άλλο σου ταιριάζει και βγαίνει η εξίσωση κύκλου.
Βάζει στην ΧΕ : 1+A(s) = 0 όπου S to x+yi
κάνεις πράξεις και έχεις
Re {1+A(x+yi) } + i *Im {1+A(x+yi)} =0
Άρα
Re {1+A(x+yi) } =0 και
Im {1+A(x+yi)} = 0
Σε αυτό το σύστημα έχει μόνο χ,y και κ
κάνεις απαλοιφή του Κ δηλαδή , λύνεις μία από τις 2 ως προς κ και το αντικαθιστάς στην άλλη
και ετσι μετά την αντακατάσταση έχει μία σχέση με χ κι y μόνο που είναι ίση με το 0
εκεί παίζεις λιγάκι με πράξεις παραγοντποιήσεις ή ότι άλλο σου ταιριάζει και βγαίνει η εξίσωση κύκλου.
thanks m8!!! twra katalaba!
pwpw re file tous gamise sthn ptixiaki pragmatika
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: erotokritos on August 29, 2010, 19:04:28 pm
οκ παιδιά ευχαριστώ πάρα πολύ .
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 19:05:14 pm
Ερώτηση σχετικά με τις απορίψεις
Τουλάχιστον 20 dB σημαίνει 20 log| Ηyd| >=20 log10 ?
To πολύ 20 dB σημαίνει 20 log| Ηyd| <=20 log10 ?
Τουλάχιστον -20 dB σημαίνει 20 log| Ηyd| >= 20 log0.1 ?
To πολύ -20 dB σημαίνει 20 log| Ηyd| <=20 log0.1 ?
Επίσης η προσέγγιση |1+Α(s)| = A(s) ισχύει για ω=0.1 και όχι για ω=1 , 10 κλπ.
Με αφορμή τα παραπάνω Θέμα 2ο ΣΕΠ 2009
Ηc= Kp(s+c)/s για να ικανοποιειται η 1η προδιαγραφή
A(s)=50 Kp(s+c) / [ s(s+3)(s+10)]
Esr<= 0.1 =>Kp*c>=6 ή ΚΙ >=6 αφού c=KI/Kp από την 2η
| Ηyd(jω)| = 1/(1+Α(s) )
Για ω=0.1 ras/sec
20log(| Ηyd(jω)| ) >= 20log(0.1) <=> ( μιας και log0.1 = -1)
| Ηyd(jω)| >= 0.1 <=>
1 / | Ηyd(jω)| <= 10 <=>
|1+Α(jω) | <=10 και εδώ χωρίς ιδιαίτερο σφάλμα
|Α(jω) | <=10
|50 Kp(j*0.1+c) / [ j*0.1(j*0.1+3)(j*0.1+10)]| <=10 <=>
|Kp(j*0.1+c| <=0.6
Kp^2 *( 0.01 +c^2) <= 0.36
Kp^2 + 100(Kp*c)^2 <=36
Kp^2 + 100(KI)^2 <=36 Το οποίο μου φαίνεται αδύνατο μιας και ΚΙ > = 6 από την 2η προδιαγραφή
Που κάνω το λάθος ;
Τουλάχιστον 20 dB σημαίνει 20 log| Ηyd| >=20 log10 ?
To πολύ 20 dB σημαίνει 20 log| Ηyd| <=20 log10 ?
Τουλάχιστον -20 dB σημαίνει 20 log| Ηyd| >= 20 log0.1 ?
To πολύ -20 dB σημαίνει 20 log| Ηyd| <=20 log0.1 ?
Επίσης η προσέγγιση |1+Α(s)| = A(s) ισχύει για ω=0.1 και όχι για ω=1 , 10 κλπ.
Με αφορμή τα παραπάνω Θέμα 2ο ΣΕΠ 2009
Ηc= Kp(s+c)/s για να ικανοποιειται η 1η προδιαγραφή
A(s)=50 Kp(s+c) / [ s(s+3)(s+10)]
Esr<= 0.1 =>Kp*c>=6 ή ΚΙ >=6 αφού c=KI/Kp από την 2η
| Ηyd(jω)| = 1/(1+Α(s) )
Για ω=0.1 ras/sec
20log(| Ηyd(jω)| ) >= 20log(0.1) <=> ( μιας και log0.1 = -1)
| Ηyd(jω)| >= 0.1 <=>
1 / | Ηyd(jω)| <= 10 <=>
|1+Α(jω) | <=10 και εδώ χωρίς ιδιαίτερο σφάλμα
|Α(jω) | <=10
|50 Kp(j*0.1+c) / [ j*0.1(j*0.1+3)(j*0.1+10)]| <=10 <=>
|Kp(j*0.1+c| <=0.6
Kp^2 *( 0.01 +c^2) <= 0.36
Kp^2 + 100(Kp*c)^2 <=36
Kp^2 + 100(KI)^2 <=36 Το οποίο μου φαίνεται αδύνατο μιας και ΚΙ > = 6 από την 2η προδιαγραφή
Που κάνω το λάθος ;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Social_waste on August 29, 2010, 19:06:07 pm
root locus ειναι η παρασταση των ριζων του Α(s)+1=1+K*Hc*Hp
καθως μεταβαλλεται το Κ. δηλαδη το σχεδιαζεις χρησιμοποιωντας
το Α αλλα σου λεει πραγματα για το Ηc.
Οι ριζες του Α οι ιδιες ειναι σταθερες και ανεξαρτητες απο το Κ.
δεν εχει νοημα να τις ζωγραφισεις.
καθως μεταβαλλεται το Κ. δηλαδη το σχεδιαζεις χρησιμοποιωντας
το Α αλλα σου λεει πραγματα για το Ηc.
Οι ριζες του Α οι ιδιες ειναι σταθερες και ανεξαρτητες απο το Κ.
δεν εχει νοημα να τις ζωγραφισεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 19:18:16 pm
στις ασκησεις με σχεδιαση επειδη στο βιβλιο τα λυνει με βαση τις γραφικες παραστασεις του matlab ^banghead^ απο α4 και θεματα
mono elegktes P kai PI xrisimopoioume..otan zitaei ess< apo kati tote pairnw k kai otan ess=0 tote pithanon PI alla prwta elegxw me k. Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...An leei xronos anodou< apo kati opws ioylios 2009 tote pairnw ts<td<apo kati giati den yparxei typos gia ton xrono anodou...Aporipsi diataraxwn toulaxiston tosa db simainei 20log|Hyd|<=20log(tosa db) kai gia aporipsh thoryvoy to idio kai isxyoyn oi proseggiseis analoga an einai mikri sixnotita se aporipsi diataraxwn kai ypsili se aporipsi thoryvou..Eyros zwnhs toulaxiston toso..tote pairnw euros zwnhs=wc, to wc bgainei apo |A(jwc)|=1.To perithwrio fasis brisketai afou prwta antikatastisw to wc sto A(jw) kai to ferw se poliki morfi kai meta θm=180+gwnia, gwnia na einai arnitiki...Perithwrio kerdous toulaxiston toso simainei oti arkei na apodeiksw oti einai apeiro apo to routh..an leei mikrotero apo mia timi tote apo routh briskw to ko(simeio tomhs tou GTP me ton fantastiko aksona) kai apo Gm=ko/kerdos<apo kati briskw mia sinthiki.To kerdos mporei na einai to k sketo alla mporei kai px 10k h kati allo..sintelestis epi k diladi. Afou brw sinthikes epilegw stin tixi times parametrwn pou ikanopoioun oles tis sinthikes.. Psilostandar auta kathe xrono peripou ta idia einai..
sorry lathos...aporipsi diataraxwn na zitaei mikri(diladi to poly) den paizei...alla kai na zitaei bazeis tin aniswsi anapoda..mono elegktes P kai PI xrisimopoioume..otan zitaei ess< apo kati tote pairnw k kai otan ess=0 tote pithanon PI alla prwta elegxw me k. Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...An leei xronos anodou< apo kati opws ioylios 2009 tote pairnw ts<td<apo kati giati den yparxei typos gia ton xrono anodou...Aporipsi diataraxwn toulaxiston tosa db simainei 20log|Hyd|<=20log(tosa db) kai gia aporipsh thoryvoy to idio kai isxyoyn oi proseggiseis analoga an einai mikri sixnotita se aporipsi diataraxwn kai ypsili se aporipsi thoryvou..Eyros zwnhs toulaxiston toso..tote pairnw euros zwnhs=wc, to wc bgainei apo |A(jwc)|=1.To perithwrio fasis brisketai afou prwta antikatastisw to wc sto A(jw) kai to ferw se poliki morfi kai meta θm=180+gwnia, gwnia na einai arnitiki...Perithwrio kerdous toulaxiston toso simainei oti arkei na apodeiksw oti einai apeiro apo to routh..an leei mikrotero apo mia timi tote apo routh briskw to ko(simeio tomhs tou GTP me ton fantastiko aksona) kai apo Gm=ko/kerdos<apo kati briskw mia sinthiki.To kerdos mporei na einai to k sketo alla mporei kai px 10k h kati allo..sintelestis epi k diladi. Afou brw sinthikes epilegw stin tixi times parametrwn pou ikanopoioun oles tis sinthikes.. Psilostandar auta kathe xrono peripou ta idia einai..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 19:23:18 pm
Πάλι δεν λύθηκε η απορία μου .... ^confused^
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Salvation on August 29, 2010, 19:37:49 pm
Όταν λέει απόρριψη διαταραχών τουλάχιστον 20 τότε παιρνουμε 20log|Hyd|<-20? Αν λέει απόρριψη -20 αλλάζει κάτι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 19:45:27 pm
Quote
Τουλάχιστον 20 dB σημαίνει 20 log| Ηyd| >=20 log10 ?
To πολύ 20 dB σημαίνει 20 log| Ηyd| <=20 log10 ?
Τουλάχιστον -20 dB σημαίνει 20 log| Ηyd| >= 20 log0.1 ?
To πολύ -20 dB σημαίνει 20 log| Ηyd| <=20 log0.1 ?
To πολύ 20 dB σημαίνει 20 log| Ηyd| <=20 log10 ?
Τουλάχιστον -20 dB σημαίνει 20 log| Ηyd| >= 20 log0.1 ?
To πολύ -20 dB σημαίνει 20 log| Ηyd| <=20 log0.1 ?
Den mpainei to poly giati den thes sto systhma sou na exei mikri aporipsi diataraxwn diladi polles diataraxes kai parasita. Τουλάχιστον 20 dB σημαίνει 20 log| Ηyd| <=20 log10 Τουλάχιστον -20 dB σημαίνει 20 log| Ηyd| <= 20 log0.1. Auta katalaba apo selida 374,378..mikri sinartisi metaforas diataraxwn liges diataraxew megali aporipsi diataraxwn....
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 20:34:10 pm
Κατάλαβα ...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kmaniac on August 29, 2010, 20:38:39 pm
Στη σε λιδα 378 παντως λεει καθαρα οτι οι αποσβεση θορυβου και η απορριψη διαταραχων ειναι πολύ μικροτερες τησ μοναδας αρα υποθετω πως ειτε σου δινει 20dB ειτε -20dB θα το περνουμε παντα αρνητικο ωστε να εχουμε Log0.1 για την παραπανω περιπτωση.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: koukou138 on August 29, 2010, 21:21:26 pm
Παίδες μια ερώτηση για το 3ο θέμα της πτυχιακής του ιούνη όποιος μπορεί να απαντήσει. Το προσεγγιστικό διάγραμμα bode πρέπει να το σχεδιάσουμε υπολογίζοντας και τα σημεία αλλαγής της κλίσης δηλαδή τα db που αντιστοιχούν στους πόλους και τα μηδενικά ή όχι? και αν ναι πως τα υπολογίζω? γραμμικές είναι οι σχέσεις αυτές?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 21:39:13 pm
Στη σε λιδα 378 παντως λεει καθαρα οτι οι αποσβεση θορυβου και η απορριψη διαταραχων ειναι πολύ μικροτερες τησ μοναδας αρα υποθετω πως ειτε σου δινει 20dB ειτε -20dB θα το περνουμε παντα αρνητικο ωστε να εχουμε Log0.1 για την παραπανω περιπτωση.
diladh aporipsi diataraxwn toulaxiston 20 dB tha to paroume -20 gia na bgei 20logHyd<20log0.1 ?? tote poia h diafora me to -20 dB? :DTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Verminoz on August 29, 2010, 21:59:25 pm
απο routh πως αποδεικνύεις ότι το περιθώριο κέρδους είναι άπειρο (ή όχι)?
Αν δε κάνω λάθος το περιθώριο κέρδους είναι Gm = 1/Am οπου
Am = | A(jwf) | όπου wf είναι η συχνότητα στην οποία το όρισμα της A(s) είναι θ = 180 + arg(A(jwc)) όπου wc η συχνότητα όπου | A(jwc) | = 1
Αν δε κάνω λάθος το περιθώριο κέρδους είναι Gm = 1/Am οπου
Am = | A(jwf) | όπου wf είναι η συχνότητα στην οποία το όρισμα της A(s) είναι θ = 180 + arg(A(jwc)) όπου wc η συχνότητα όπου | A(jwc) | = 1
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: gate4 on August 29, 2010, 22:01:36 pm
anyway και απο σαε 2 πετριδης για απορριψη διαταραχων τα ιδια λεει σελιδα 214... Το μετρο της απορριψης διαταραχων πρεπει να μικρο για να εχουμε λιγες διαταραχες.<100 <1000 δεν εχει σχεση...Οταν το μετρο της απορριψης διαταραχων ειναι <<1 για χαμηλες συχνοτητες ισχυει A(jw)>>1
verminoz apodeiknyeis eystatheia ara apeiro perithwrio kerdous
verminoz apodeiknyeis eystatheia ara apeiro perithwrio kerdous
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 22:04:42 pm
απο routh πως αποδεικνύεις ότι το κέρδος είναι άπειρο (ή όχι)?
Προφανώς θα έχεις μέσα ως μεταβλητή το κέρδος Κ
Αν βρεις πως το σύστημα είναι ευσταθές για κάθε Κ τότε έχουμε άπειρο κέρδος...
Προσοχή αν και στον ΓΤΡ δουλεύουμε με την Α(s) εδώ στο Routh θα πάρεις την Α(S) +1
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Verminoz on August 29, 2010, 22:06:57 pm
Απ'όσο καταλαβαίνω για ΓΤΡ και bode δουλεύουμε με την ανοιχτού βρόχου αλλά προφανώς για Routh έχει σημασία να είναι ευσταθής η κλειστού βρόχου οπότε παίρνουμε A(s) + 1.
Προφανώς θα έχεις μέσα ως μεταβλητή το κέρδος Κ
Αν βρεις πως το σύστημα είναι ευσταθές για κάθε Κ τότε έχουμε άπειρο κέρδος...
Αν τίθεται οποιοσδήποτε περιορισμός, είτε άνω είτε κάτω, για το Κ τότε ΔΕΝ έχουμε άπειρο περιθώριο κέρδους έτσι?
απο routh πως αποδεικνύεις ότι το κέρδος είναι άπειρο (ή όχι)?
Προφανώς θα έχεις μέσα ως μεταβλητή το κέρδος Κ
Αν βρεις πως το σύστημα είναι ευσταθές για κάθε Κ τότε έχουμε άπειρο κέρδος...
Αν τίθεται οποιοσδήποτε περιορισμός, είτε άνω είτε κάτω, για το Κ τότε ΔΕΝ έχουμε άπειρο περιθώριο κέρδους έτσι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 22:10:35 pm
Παίδες μια ερώτηση για το 3ο θέμα της πτυχιακής του ιούνη όποιος μπορεί να απαντήσει. Το προσεγγιστικό διάγραμμα bode πρέπει να το σχεδιάσουμε υπολογίζοντας και τα σημεία αλλαγής της κλίσης δηλαδή τα db που αντιστοιχούν στους πόλους και τα μηδενικά ή όχι? και αν ναι πως τα υπολογίζω? γραμμικές είναι οι σχέσεις αυτές?
Κανονικά το κάνεις ποιοτικά κατά κάποιο τρόπο αλλά επειδή δεν έχουμε λογαριθμική κλίμακα είναι να βρίσκεις και τις τιμές αυτές προσεγγιστικά αν θες.
Πως τις βρίσκεις ? Όπως και την ωc. Δηλαδή 20logH(s) και βάσεις όπου s το αντίστοιχο ω .
Πρόσεξε είναι η προσσεγιστικόδιάγραμμα και έτσι παίρνουμε ΜΟΝΟ το φανταστικό μέρος..
Γενικά όμως να θυμάσαι πως ξεκινάς με 20log (α) όπου α το σταθερό νούμερο που βγαίει έξω από τη συνάρτηση
Πόλος= κλίση - 20 dB
Mηδενικό= κλίση +20 dB
και αν έχεις και το ωc συνήθως το βγάζεις άντετα με το μάτι..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 22:12:14 pm
Απ'όσο καταλαβαίνω για ΓΤΡ και bode δουλεύουμε με την ανοιχτού βρόχου αλλά προφανώς για Routh έχει σημασία να είναι ευσταθής η κλειστού βρόχου οπότε παίρνουμε A(s) + 1.
Προφανώς θα έχεις μέσα ως μεταβλητή το κέρδος Κ
Αν βρεις πως το σύστημα είναι ευσταθές για κάθε Κ τότε έχουμε άπειρο κέρδος...
Αν τίθεται οποιοσδήποτε περιορισμός, είτε άνω είτε κάτω, για το Κ τότε ΔΕΝ έχουμε άπειρο περιθώριο κέρδους έτσι?
απο routh πως αποδεικνύεις ότι το κέρδος είναι άπειρο (ή όχι)?
Προφανώς θα έχεις μέσα ως μεταβλητή το κέρδος Κ
Αν βρεις πως το σύστημα είναι ευσταθές για κάθε Κ τότε έχουμε άπειρο κέρδος...
Αν τίθεται οποιοσδήποτε περιορισμός, είτε άνω είτε κάτω, για το Κ τότε ΔΕΝ έχουμε άπειρο περιθώριο κέρδους έτσι?
Εννοείς να πρέπει πχ να ισχύει κ<12 για να είναι ευσταθές ε? Όχι δεν είναι άπειρο το κέρδος , έτσι νομίζω τουλάχιστον...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Verminoz on August 29, 2010, 22:22:28 pm
Παίδες μια ερώτηση για το 3ο θέμα της πτυχιακής του ιούνη όποιος μπορεί να απαντήσει. Το προσεγγιστικό διάγραμμα bode πρέπει να το σχεδιάσουμε υπολογίζοντας και τα σημεία αλλαγής της κλίσης δηλαδή τα db που αντιστοιχούν στους πόλους και τα μηδενικά ή όχι? και αν ναι πως τα υπολογίζω? γραμμικές είναι οι σχέσεις αυτές?
http://www.swarthmore.edu/NatSci/echeeve1/Ref/LPSA/Bode/BodeRules.html
δες λίγο κι εδώ. Ο τρόπος του για το διάγραμμα πλάτους είναι πολύ καλός. Στο διάγραμμα φάσης είναι που μπερδεύομαι εγώ. :( Έχει κανείς κάποιο πιο πρακτικό τρόπο?
Εννοείς να πρέπει πχ να ισχύει κ<12 για να είναι ευσταθές ε? Όχι δεν είναι άπειρο το κέρδος , έτσι νομίζω τουλάχιστον...
Ναι αυτό εννοούσα! ΟΚ ευχαριστώ!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 29, 2010, 22:28:52 pm
Παίδες μια ερώτηση για το 3ο θέμα της πτυχιακής του ιούνη όποιος μπορεί να απαντήσει. Το προσεγγιστικό διάγραμμα bode πρέπει να το σχεδιάσουμε υπολογίζοντας και τα σημεία αλλαγής της κλίσης δηλαδή τα db που αντιστοιχούν στους πόλους και τα μηδενικά ή όχι? και αν ναι πως τα υπολογίζω? γραμμικές είναι οι σχέσεις αυτές?
Κανονικά το κάνεις ποιοτικά κατά κάποιο τρόπο αλλά επειδή δεν έχουμε λογαριθμική κλίμακα είναι να βρίσκεις και τις τιμές αυτές προσεγγιστικά αν θες.
Πως τις βρίσκεις ? Όπως και την ωc. Δηλαδή 20logH(s) και βάσεις όπου s το αντίστοιχο ω .
Πρόσεξε είναι η προσσεγιστικόδιάγραμμα και έτσι παίρνουμε ΜΟΝΟ το φανταστικό μέρος..
Γενικά όμως να θυμάσαι πως ξεκινάς με 20log (α) όπου α το σταθερό νούμερο που βγαίει έξω από τη συνάρτηση
Πόλος= κλίση - 20 dB
Mηδενικό= κλίση +20 dB
και αν έχεις και το ωc συνήθως το βγάζεις άντετα με το μάτι..
to ωc=5 ειναι στο μεσο της πλαγιας γραμμης
δεν ξερω αν εγινα σαφης
____0,1ωc
\
\---------------ωc
\___________
10ωc
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 29, 2010, 23:07:15 pm
kkostorp στο Θέμα 2ο Σεπτ 2009 η A(s) μου βγαίνει
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 23:24:17 pm
kkostorp στο Θέμα 2ο Σεπτ 2009 η A(s) μου βγαίνει
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
Μισό λεπτό!
Ξεκινάμε
Αναλογικός Ηc=k
A(s)= 50*k/[(s+3)(s+10)]
kp = lim(s->0) {A(s) } = 50k/30
ess=1/(1+kp) >0 ΆΡΑ ΑΠΟΡΊΠΤΕΤΑΙ
Επόμενη δοκιμή PI
Hc= Kp+KI/s = Kp(s+c)/s όπου c=ΚΙ/Kp
A(S) = Hc*Hp = 50*Kp*(S+c)/[s(s+3)(s+10)]
ess= 0 Σωστό άρα πάμε στην 2η προδιαγραφή κλπ...
Τι διαφορετικό κάνεις?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 29, 2010, 23:25:33 pm
kkostorp στο Θέμα 2ο Σεπτ 2009 η A(s) μου βγαίνει
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
(50 + (cs + 1)Ki(s+3)(s+10)) / s*(s+3)(s+10)
Μισό λεπτό!
Ξεκινάμε
Αναλογικός Ηc=k
A(s)= 50*k/[(s+3)(s+10)]
kp = lim(s->0) {A(s) } = 50k/30
ess=1/(1+kp) >0 ΆΡΑ ΑΠΟΡΊΠΤΕΤΑΙ
Επόμενη δοκιμή PI
Hc= Kp+KI/s = Kp(s+c)/s όπου c=ΚΙ/Kp
A(S) = Hc*Hp = 50*Kp*(S+c)/[s(s+3)(s+10)]
ess= 0 Σωστό άρα πάμε στην 2η προδιαγραφή κλπ...
Τι διαφορετικό κάνεις?
Στην 4η συνθήκη τι κάνεις?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 29, 2010, 23:29:16 pm
[
Wooops, έκανα + αντί για * :P
Στην 4η συνθήκη τι κάνεις?
Wooops, έκανα + αντί για * :P
Στην 4η συνθήκη τι κάνεις?
https://www.thmmy.gr/smf/index.php?topic=34306.15 Δες εδώ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 29, 2010, 23:56:57 pm
[
Wooops, έκανα + αντί για * :P
Στην 4η συνθήκη τι κάνεις?
Wooops, έκανα + αντί για * :P
Στην 4η συνθήκη τι κάνεις?
https://www.thmmy.gr/smf/index.php?topic=34306.15 Δες εδώ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 30, 2010, 00:09:37 am
Βρήκες τιμές αποδεκτές?
Το περιθώριο κέρδους είναι άπειρο έτσι κι αλλιώς σωστά?
Το περιθώριο κέρδους είναι άπειρο έτσι κι αλλιώς σωστά?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 30, 2010, 00:48:16 am
Βρήκες τιμές αποδεκτές?
Το περιθώριο κέρδους είναι άπειρο έτσι κι αλλιώς σωστά?
Δεν την πήγα μέχρι τέλους...Το περιθώριο κέρδους είναι άπειρο έτσι κι αλλιώς σωστά?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Verminoz on August 30, 2010, 02:04:18 am
φλεβάρης 2009 θέμα 2ο τι βρήκατε σαν τελικό σύστημα?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 30, 2010, 02:17:47 am
ασχετο...τελικα οταν εχω |Α+1|>10 την κανω την προσεγγιση |Α|>10 η οχι?
νομιζω ο πετριδης μπορει να κοβει αν κανεις προσεγγισεις...
νομιζω ο πετριδης μπορει να κοβει αν κανεις προσεγγισεις...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 30, 2010, 02:42:31 am
ασχετο...τελικα οταν εχω |Α+1|>10 την κανω την προσεγγιση |Α|>10 η οχι?
νομιζω ο πετριδης μπορει να κοβει αν κανεις προσεγγισεις...
Νομίζω γίνεται αυτό ρε...νομιζω ο πετριδης μπορει να κοβει αν κανεις προσεγγισεις...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 30, 2010, 02:45:21 am
νομιζω μου'λεγε ο γιαννης παλια που το'χα δωσει να μην το κανω αυτο γιατι ο πετριδης ειναι ανωμαλος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 30, 2010, 02:52:36 am
νομιζω μου'λεγε ο γιαννης παλια που το'χα δωσει να μην το κανω αυτο γιατι ο πετριδης ειναι ανωμαλος
μόνο με ανωμαλία κόβεις τέτοια. Σε λίγο θα ζητάει να βγάζουμε αποτελέσματα Matlab με το μυαλό μας ^idiot^Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vicariously,I on August 30, 2010, 02:55:46 am
θελω να πω οτι,πρωτα ο θεος, του γαμιεται η μανα..
βλεπεις τον βανω τον θεο και στο παρελθον..
βλεπεις τον βανω τον θεο και στο παρελθον..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kkostorp on August 30, 2010, 10:45:56 am
Διάγραμμα Bode για μία συνάρτηση με πόλο στο 0 έστω
Η= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
Η= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Salvation on August 30, 2010, 10:50:15 am
Ρε παιδιά όταν μου δίνει ευρος ζώνης τουλάχιστον wb>10.Παιρνω την εξίσωση |Α(jw)|=1 και μετά τη λύνω για να βρω το wc? Βγαίνουνε άπειρες πράξεις και πολύ μεγάλες δυνάμεις. Γίνεται να βοηθήσει κάποιος;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 30, 2010, 11:01:56 am
Στα αθροίσματα με λογαρίθμους τι προσεγγίσεις παίρνουμε? Π.χ. για να βρούμε ωb και τέτοια...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Anyparktos on August 30, 2010, 11:10:30 am
Ετσι πως το σκεφτομαι εγω αμα παρεις λογαριθμους με προσεγγιστικο bode γινεται η κολαση η ιδια γιατι δε ξερεις την περιοχη του ωc εκ των προτερων,ειδικα αν κανεις σχεδιαση οποτε μπορει να λαβεις υποψη καποιους πολους οι οποίοι δίνουν τιμή κέρδους μηδεν στο προσεγγιστικο bode κερδους κοντα στην τιμή που τελικα θα προκυψει στο ωc.Αυτο που σε καλυπτει πληρως ειναι να κανεις τις πραξεις με μετρα μιγαδικων.Ναι μεν,θα σου βγουν ΤΟΥΛΑΧΙΣΤΟΝ δευτεροβαθμιες ως προς τους αγνωστους αλλα θα ειναι σιγουρα σχεσεις που ισχυουν.Μια αλλη ιδεα που εχω ειναι να παρεις οτι το ωc ειναι μεγαλυτερο ή ισο απο την τιμη Bandwidth που σου δινει.Αυτο το σκεφτηκα γιατι τα Bode κερδους εχουν θετικη τιμη πριν μηδενιστουν.Οποτε αν παρεις |Α(jωc)|>=1 ,όπου ωc το ελαχιστο bandwidth που εχεις απο την προδιαγραφη της εκφωνησης,εισαι καλυμμενος...Κανω λαθος?
ΕDIT:
Επισης ενα αλλο πραμα που παρατηρησα:Το κριτηριο του bandwidth συνηθως υπερκαλυπτεται κατα πολυ απο τα υπολοιπα κριτηρια που εχουμε.Δλδ αν μπορεσουμε να μαντεψουμε καποιες τιμες που ικανοποιουν τις υπολοιπες σχεσεις που εχουμε συνηθως αν παμε να βρουμε μετα το ωc μας προκυπτει μεγαλυτερο του οριου που δινει στην εκφωνηση για το Bandwidth.Προφανως αυτο δεν ισχυει παντα,αλλα αυτο που σκεφτηκα ειναι να χρησιμοποιουμε αυτη την προδιαγραφη μονο ως επαληθευση στο τελος...I dunno if any of this makes sense...
ΕDIT:
Επισης ενα αλλο πραμα που παρατηρησα:Το κριτηριο του bandwidth συνηθως υπερκαλυπτεται κατα πολυ απο τα υπολοιπα κριτηρια που εχουμε.Δλδ αν μπορεσουμε να μαντεψουμε καποιες τιμες που ικανοποιουν τις υπολοιπες σχεσεις που εχουμε συνηθως αν παμε να βρουμε μετα το ωc μας προκυπτει μεγαλυτερο του οριου που δινει στην εκφωνηση για το Bandwidth.Προφανως αυτο δεν ισχυει παντα,αλλα αυτο που σκεφτηκα ειναι να χρησιμοποιουμε αυτη την προδιαγραφη μονο ως επαληθευση στο τελος...I dunno if any of this makes sense...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 30, 2010, 12:49:21 pm
Διάγραμμα Bode για μία συνάρτηση με πόλο στο 0 έστω
Η= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
svsto se brisko alla sto telos afaireis oti briskeis apo to 180 και αυτο ειναι το περιθωριο φασηςΗ= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Anyparktos on August 30, 2010, 13:29:29 pm
Δεν το αφαιρεις.Το ορισμα της A(jωc) βγαίνει παντα αρνητικό οπότε πρέπει να πάρεις αλγεβρικό άθροισμα αλλιώς θα βγάλεις φm>180o.Δηλαδή είναι φm=180o + <A(jωc)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Stu@rt on August 30, 2010, 13:35:21 pm
Δεν το αφαιρεις.Το ορισμα της A(jωc) βγαίνει παντα αρνητικό οπότε πρέπει να πάρεις αλγεβρικό άθροισμα αλλιώς θα βγάλεις φm>180o.Δηλαδή είναι φm=180o + <A(jωc)
ayto ennooysa ...pali kala omos min ginotan kana lathos kai 180- (- A(jωc)):P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SolidSNK on August 30, 2010, 14:05:34 pm
Διάγραμμα Bode για μία συνάρτηση με πόλο στο 0 έστω
Η= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
svsto se brisko alla sto telos afaireis oti briskeis apo to 180 και αυτο ειναι το περιθωριο φασηςΗ= (s+20)/[s(s+5)(s+2)] = 10* (s/20 +10 )/ [ s (s/5+1) (s/2+1)]
Για να βρω ωc
log10 + log(ωc/20) - log(ωc) - log(ωc/5) -log(ωc/2) = log1 ????
Φm = arctan(ωc/20) - arctan(ωc)- arctan(ωc/50) -arctan(ωc/2) ????
Μπορεί κάποιος να μου πει αν είναι σωστό ή λάθος ???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pumba on January 21, 2012, 15:30:10 pm
Στο 1ο θεμα ΣΕΠΤΕΜΒΡΙΟΣ 2009,η συνθηκη μας καταληγει να ειναι α>3,1. Παιρνοντας ομως δυο διαφορετικες τιμες (π.χ. α=3,5 και α=5) καταληγουμε να εχουμε δυο εντελως διαφορετικους ΓΤΡ. Το ερωτημα μου ειναι: ειναι κ οι 2 λυσεις σωστες ή υπαρχει και καποια αλλη συνθηκη που πρεπει να λαβουμε υποψιν?? Επειδη θυμαμαι να λεει η δουλγερη στην ταξη οτι ο πολος μας θα πρεπει να ειναι κοντα στο μηδενικο για να βελτιωθει η ταχυτητα και κατι τετοια....Οποιος θυμαται ή γνωριζει,ας απαντησει, pleazzz....
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Professional Hater on January 25, 2013, 21:26:28 pm
Μπορεί κάποιο κάλο παιδάκι να μου εξηγήσει τον τύπο της σελίδας 319 (πετρίδη) που λέει για τις γωνίες άφιξης? Δεν καταλαβαίνω τι βάζω για όρισμα π.χ. του s-3.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Professional Hater on January 25, 2013, 23:02:07 pm
Στο 1ο θεμα ΣΕΠΤΕΜΒΡΙΟΣ 2009,η συνθηκη μας καταληγει να ειναι α>3,1. Παιρνοντας ομως δυο διαφορετικες τιμες (π.χ. α=3,5 και α=5) καταληγουμε να εχουμε δυο εντελως διαφορετικους ΓΤΡ. Το ερωτημα μου ειναι: ειναι κ οι 2 λυσεις σωστες ή υπαρχει και καποια αλλη συνθηκη που πρεπει να λαβουμε υποψιν?? Επειδη θυμαμαι να λεει η δουλγερη στην ταξη οτι ο πολος μας θα πρεπει να ειναι κοντα στο μηδενικο για να βελτιωθει η ταχυτητα και κατι τετοια....Οποιος θυμαται ή γνωριζει,ας απαντησει, pleazzz....
Γενικά υπάρχει καλύτερη και χειρότερη λύση αλλά η Δουλγέρη είπε πως άμα τηρούνται οι προδιαγραφές είναι σωστή η λύση και δεν χάνεις μονάδες ακόμα κι αν έχεις επιλέξει τη χειρότερη. Δηλαδή και τα δύο σωστά είναι. Τώρα ποιο είναι πιο σωστό δεν ξέρω :DTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: teslaaaa on January 26, 2013, 01:50:09 am
ακομα και βελτιστη λυση να υπηρχε δεν θα τη ζητουσε ετσι ξερα, αλλα ως προς πιο περιορισμο θελουμε την καλυτερη λυση,διοτι υπαρχει και ενα trade-off μη ξεχνιομαστε..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pepper ann on January 26, 2013, 11:46:28 am
παιδιααααα υπάρχουν κάπου οι εκφωνήσεις των θεμάτων φεβ 2006 και φεβ 2009???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: chrimour on January 26, 2013, 15:04:53 pm
σε περιπτωση που εχουμε να σχεδιασουμε ΓΤΡ οπως την περιπτωση του Φεβρουαριου 2008 θεμα 2ο με Α(s)=Κ(s+12)/((s+1)(s+4)(s+5)) θα πρεπει να βρισκουμε και το σημειο αποσχισης η θα πρεπει να το βαζουμε εμπειρικα; επειδη αν κανεις την παραγωγο dA(s)/ds βγαινει ενα μακρυναρι σχεδον απιθανον να λυθει στο χερι.. βασικα σε τετοιες περιπτωσεις πως το δουλευουμε;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: teslaaaa on January 26, 2013, 16:00:37 pm
ο πετριδης ειχε πει στο μαθημα νομιζω οτι καποιες φορες το σημειο αποσχισης ταυτιζεται με το σημειο τομης των ασυμπτωτων (διανυσμα ΟΑ). Οποτε μπορεις να ελεγξεις απλα αν το σημειο Α μηδενιζει την παραγωγο της Α(s)...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Infinite Loop on January 26, 2013, 17:09:55 pm
ο πετριδης ειχε πει στο μαθημα νομιζω οτι καποιες φορες το σημειο αποσχισης ταυτιζεται με το σημειο τομης των ασυμπτωτων (διανυσμα ΟΑ). Οποτε μπορεις να ελεγξεις απλα αν το σημειο Α μηδενιζει την παραγωγο της Α(s)...
Νομιζω οτι αυτο ειναι μουφα. Και αλλωστε, ακομα και να ισχυε, δεν μπορεις να εμπιστευεσαι το "καποιες φορες". Προς το παρον δεν εχω βρει καποιον πιο απλο τροπο απο το να βρεις τις ριζες τις παραγωγου. Για να γλυτωσεις λιγο χρονο, η εξισωση που βγαινει ειναι η D(s)dN(s)/ds=N(s)dD(s)/ds, που στην χειροτερη ειναι n+m-1 βαθμου - που σημαινει οτι αν π.χ. εχεις 4 πολους και 2 μηδενικα, την εκατσες...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 26, 2013, 18:11:10 pm
οταν λεμε κερδος στην Α(s) εννοουμε το k, αν η Α ειναι της μορφης: k(s+a)/(s+b)
οταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
οταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pepper ann on January 26, 2013, 18:30:12 pm
οταν λεμε κερδος στην Α(s) εννοουμε το k, αν η Α ειναι της μορφης: k(s+a)/(s+b)
οταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
εγώ καταρχήν θα έλεγα ότι το κέρδος της A(s) είναι κ*a/b :Pοταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Infinite Loop on January 26, 2013, 18:34:31 pm
οταν λεμε κερδος στην Α(s) εννοουμε το k, αν η Α ειναι της μορφης: k(s+a)/(s+b)
οταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
εγώ καταρχήν θα έλεγα ότι το κέρδος της A(s) είναι κ*a/b :Pοταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
Αυτο ειναι το DC κερδος. Αμα μιλαμε ομως (οπως ειναι πιθανον) για ΓΤΡ, τοτε σαν "κερδος" εννοουμε την παραμετρο που μεταβαλλεται, δηλαδη το k.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 26, 2013, 18:51:12 pm
οταν λεμε κερδος στην Α(s) εννοουμε το k, αν η Α ειναι της μορφης: k(s+a)/(s+b)
οταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
εγώ καταρχήν θα έλεγα ότι το κέρδος της A(s) είναι κ*a/b :Pοταν λεμε κερδος στην Α(s) η οποια ειναι της μορφης 15*k(s+a)/(s+b)
τοτε εννοουμε το 15*k ή το k? :-\
Αυτο ειναι το DC κερδος. Αμα μιλαμε ομως (οπως ειναι πιθανον) για ΓΤΡ, τοτε σαν "κερδος" εννοουμε την παραμετρο που μεταβαλλεται, δηλαδη το k.
ναι συμφωνω.. απλα το γτρ τον φτιαχνεις ανεξαρτητα απο τη μεταβλητη και τους συντελεστες της .
οποτε ουσιαστικα αυτο που μεταβαλλεται ειναι το 15*κ.. σαν κερδος θα θεωρησουμε το κ ή το 15*κ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Souras on January 27, 2013, 01:00:54 am
ναταλία η δουλγέρη είπε ότι θεωρείς το 15*κ στην συγκεκριμένη περίπτωση..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: teslaaaa on January 27, 2013, 13:07:01 pm
καλημερα! να κανω μια "χαζη" ερωτηση? στο 1ο θεμα ιουνιος 2007 θελει τ σφαλματα κ μ τις 2 εισοδους μη μηδενικες?επισης r(s) ειναι ο laplace της ραμπας?
επισης στην ιδια χρονια αλλα στο 3ο θεμα στο δ)ζηταει απορριψη διαταραχων για μεγαλες συχνοτητες..οι διαταραχες στις χαμηλες συχνοτητες δεν υποτιθεται οτι εμφανιζονται?wtf??? :???:
επισης στην ιδια χρονια αλλα στο 3ο θεμα στο δ)ζηταει απορριψη διαταραχων για μεγαλες συχνοτητες..οι διαταραχες στις χαμηλες συχνοτητες δεν υποτιθεται οτι εμφανιζονται?wtf??? :???:
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 27, 2013, 23:50:40 pm
Μπορει καποιος να πει πως εξεταζονται οι προδιαγραφες 4,5 (θm και gm) στο δευτερο θεμα Ιανουαριου 2012
με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 00:28:59 am
Μπορει καποιος να πει πως εξεταζονται οι προδιαγραφες 4,5 (θm και gm) στο δευτερο θεμα Ιανουαριου 2012
με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
που ειναι αυτο το θεμα? :S
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 00:47:28 am
Έίναι το περσινό θέμα σχεδίασης:
Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: niko on January 28, 2013, 01:05:48 am
Μπορει καποιος να πει πως εξεταζονται οι προδιαγραφες 4,5 (θm και gm) στο δευτερο θεμα Ιανουαριου 2012
με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
νομιζω ειναι αυτο που λεει σελ 377 αν |1+Α(jω)|>0.5=>|S(jω)|<2 τοτε gm > 2 και θm > 30με τη συνθηκη για τη συναρτηση ευαισθησιας S(jω) ??
λυνεις και ισχυει για κάθε ω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 01:08:45 am
ναι αυτο ειναι..
κανεις bode στην S και βλεπεις να μην ξεπερασει τη τιμη 20log2
κανεις bode στην S και βλεπεις να μην ξεπερασει τη τιμη 20log2
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 01:15:08 am
Sωστα δεν το ειχα σκεφτει thanks :)
Θα πρεπει να εχω δωσει τιμες στα Kp, Ki για να κανω Bode?
Θα πρεπει να εχω δωσει τιμες στα Kp, Ki για να κανω Bode?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 01:15:38 am
Sωστα δεν το ειχα σκεφτει thanks :)
Θα πρεπει να εχω δωσει τιμες στα Kp, Ki για να κανω Bode?
Θα πρεπει να εχω δωσει τιμες στα Kp, Ki για να κανω Bode?
υποθετω ναι!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ValmadiaN on January 28, 2013, 01:17:57 am
Στο 2ο θέμα του Ιανουαρίου 2011:
Ζητάει στο ερώτημα β) χρόνο αποκατάστασης το πολύ 1s.
Για να ισχύει κάτι τέτοιο θα πρέπει όλοι οι πόλοι να έχουν πραγματικό μέρος
-σ<= -4.16/1 (προσεγγιστικά σύμφωνα με τους τύπους για τα συστήματα 2ης τάξης)
Αν χρησιμοποιήσουμε ελεγκτή PI προκύπτει Α(s)=k(s+c)(s+2)/(s(s+3)(s+6)).
Το θέμα είναι (φαίνεται από τον ΓΤΡ) ότι από τη στιγμή που υπάρχει μηδενικό στο -2 και πόλος στο 0,
πάντα κάποιος πόλος θα κινείται ανάμεσα στο -2 και το 0 οπότε δεν μπορεί να ικανοποιηθεί το ζητούμενο.
Κάνω κάπου λάθος ή έχω δίκιο και θα πρέπει να πάμε σε ελεγκτή PID; :D :D
ΥΓ: Δεν μπορούμε να χρησιμοποιήσουμε αναλογικό ελεγκτή επειδή ζητάει πεπερασμένο σφάλμα ταχύτητας και
άρα χρειάζομαι 1 ολοκληρωτή στην Α(s).
Ζητάει στο ερώτημα β) χρόνο αποκατάστασης το πολύ 1s.
Για να ισχύει κάτι τέτοιο θα πρέπει όλοι οι πόλοι να έχουν πραγματικό μέρος
-σ<= -4.16/1 (προσεγγιστικά σύμφωνα με τους τύπους για τα συστήματα 2ης τάξης)
Αν χρησιμοποιήσουμε ελεγκτή PI προκύπτει Α(s)=k(s+c)(s+2)/(s(s+3)(s+6)).
Το θέμα είναι (φαίνεται από τον ΓΤΡ) ότι από τη στιγμή που υπάρχει μηδενικό στο -2 και πόλος στο 0,
πάντα κάποιος πόλος θα κινείται ανάμεσα στο -2 και το 0 οπότε δεν μπορεί να ικανοποιηθεί το ζητούμενο.
Κάνω κάπου λάθος ή έχω δίκιο και θα πρέπει να πάμε σε ελεγκτή PID; :D :D
ΥΓ: Δεν μπορούμε να χρησιμοποιήσουμε αναλογικό ελεγκτή επειδή ζητάει πεπερασμένο σφάλμα ταχύτητας και
άρα χρειάζομαι 1 ολοκληρωτή στην Α(s).
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: DoomGuard on January 28, 2013, 01:23:52 am
Στο 2ο θέμα του Ιανουαρίου 2011:
Ζητάει στο ερώτημα β) χρόνο αποκατάστασης το πολύ 1s.
Για να ισχύει κάτι τέτοιο θα πρέπει όλοι οι πόλοι να έχουν πραγματικό μέρος
-σ<= -4.16/1 (προσεγγιστικά σύμφωνα με τους τύπους για τα συστήματα 2ης τάξης)
Αν χρησιμοποιήσουμε ελεγκτή PI προκύπτει Α(s)=k(s+c)(s+2)/(s(s+3)(s+6)).
Το θέμα είναι (φαίνεται από τον ΓΤΡ) ότι από τη στιγμή που υπάρχει μηδενικό στο -2 και πόλος στο 0,
πάντα κάποιος πόλος θα κινείται ανάμεσα στο -2 και το 0 οπότε δεν μπορεί να ικανοποιηθεί το ζητούμενο.
Κάνω κάπου λάθος ή έχω δίκιο και θα πρέπει να πάμε σε ελεγκτή PID; :D :D
ΥΓ: Δεν μπορούμε να χρησιμοποιήσουμε αναλογικό ελεγκτή επειδή ζητάει πεπερασμένο σφάλμα ταχύτητας και
άρα χρειάζομαι 1 ολοκληρωτή στην Α(s).
Ζητάει στο ερώτημα β) χρόνο αποκατάστασης το πολύ 1s.
Για να ισχύει κάτι τέτοιο θα πρέπει όλοι οι πόλοι να έχουν πραγματικό μέρος
-σ<= -4.16/1 (προσεγγιστικά σύμφωνα με τους τύπους για τα συστήματα 2ης τάξης)
Αν χρησιμοποιήσουμε ελεγκτή PI προκύπτει Α(s)=k(s+c)(s+2)/(s(s+3)(s+6)).
Το θέμα είναι (φαίνεται από τον ΓΤΡ) ότι από τη στιγμή που υπάρχει μηδενικό στο -2 και πόλος στο 0,
πάντα κάποιος πόλος θα κινείται ανάμεσα στο -2 και το 0 οπότε δεν μπορεί να ικανοποιηθεί το ζητούμενο.
Κάνω κάπου λάθος ή έχω δίκιο και θα πρέπει να πάμε σε ελεγκτή PID; :D :D
ΥΓ: Δεν μπορούμε να χρησιμοποιήσουμε αναλογικό ελεγκτή επειδή ζητάει πεπερασμένο σφάλμα ταχύτητας και
άρα χρειάζομαι 1 ολοκληρωτή στην Α(s).
Δίκιο έχεις και εγώ προσπαθούσα ώρα να βγάλω άκρη αλλά δεν κατέληξα κάπου και το άφησα γιατί μου έτρωγε χρόνο.
Προσπάθησα μέχρι και να απαλείψω το μηδενικό στο 2..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 01:29:38 am
Έίναι το περσινό θέμα σχεδίασης:
Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
τι συνθηκες βρηκες? :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ValmadiaN on January 28, 2013, 01:42:59 am
Δίκιο έχεις και εγώ προσπαθούσα ώρα να βγάλω άκρη αλλά δεν κατέληξα κάπου και το άφησα γιατί μου έτρωγε χρόνο.
Προσπάθησα μέχρι και να απαλείψω το μηδενικό στο 2..
Προσπάθησα μέχρι και να απαλείψω το μηδενικό στο 2..
Να κάτι που βρήκα σε παλαιότερο τόπικ. Για όσους παιδεύονται με το αντίστοιχο θέμα!
Το ζ και το ω ορίζονται για χαρακτηριστικά πολυώνυμα 2ου βαθμού. Πώς πήρες ότι 2ζω=9+κ ?
Απλά στη θεωρία κάνουμε μία επέκταση και λέμε ότι και για συστήματα μεγαλύτερου βαθμού απο 2 μπορούμε να προσεγγίσουμε τον χρόνο αποκατάστασης από τη θέση του κύριου πόλου ως ts=4.16/σ , όπου σ η θέση του κύριου πόλου στον αρνητικό πραγματικό άξονα.
Αν κάνει κανείς τον ΓΤΡ θα δεί ότι όπου και να τοποθετηθεί το μηδενικό c του PI ελεγκτή, το καλύτερο ts που μπορούμε να πετύχουμε είναι 4.16/2 = περίπου 2. Και αυτό για πολύ μεγάλες τιμές του κέρδους ώστε ο πόλος στο 0 να προσεγγίζει το μηδενικό στο -2.
Η προδιαγραφή αυτή με την ύλη των ΣΑΕ 1 είναι αδύνατη και έπεσε πολύ κράξιμο τον χειμώνα στον Πετρίδη. Τελικά βαθμολογήθηκαν με όλες τις μονάδες οι λύσεις που έλεγαν ότι είναι αδύνατη η ικανοποίησή της και το τεκμηρίωναν. Όσοι προσπάθησαν πατέντες με περίεργους ελεγκτές μπας και κάνουν τίποτα πήραν τα @@ τους.
Για το 4δ , αν και δεν το είχα πιάσει εκείνη την ώρα η σκέψη μου είναι η εξης:
Συνολικά η συνάρτησή μας έχει 2 μηδενικά και 3 πόλους. Για να βρούμε το περιθώριο φάσης , πρέπει να βρούμε τη συχνότητα ωc όπου το διάγραμμα bode κέρδους μηδενίζεται, δηλαδή θέτουμε το μέτρο της συνάρτησης ίσο με 1 , s=jωc, υψώνουμε στο τετράγωνο και λύνουμε ώς προς ωc. Επειδή έχω 3 πόλους, ο παρονομαστής θα μας δώσει όρο ω^6 , οπότε δε μπορούμε να λύσουμε αναλυτικά.
Αφού έχω την δυνατότητα επιλογής του ενός μηδενικου, δηλαδή του c=Ki/Kp , το παίρνω ίσο με 3 για να μου απαλείψει τον έναν πόλο. Έτσι η συνάρτησή μου προκύπτει:
Κp(s+2)/(s+3)(s+6)
Από το α) εύκολα βγάζω Ki>18 οπότε επιλέγω Ki=21, άρα kp=21/3=7 . Μπορεί να επιλέξει κανείς και διαφορετικό προφανώς. Με kp = 7 η παραπάνω διαδικασία μας δίνει ωc=4.19 Ηζ και περιθώριο φάσης 119 μοίρες που είναι αποδεκτό.
Τέλος για το γ) , απο ΓΤΡ μπορώ να δώ ότι το κέρδος μου είναι άπειρο. Αυτά.
Τώρα η απαλοιφή πόλου δε ξέρω κατά πόσο είναι πρακτικά καλη ιδέα, στα ΣΑΕ 2 είχε κάτι περίεργα που έλεγε ότι άλλες συναρτήσεις που θα προκύψουν σε άλλα προβλήματα μπορεί να είναι ασταθείς αλλα προφανώς δε μας νοιάζει. Δε ξέρω αν θα είχε πρόβλημα με αυτό ο πετρίδης , αλλά δε μπορώ να σκεφτώ άλλον τρόπο για να απαλαχθείς απο τις πράξεις για το δ.
Αν έχετε κάποια άλλη ιδέα παρακαλω μοιραστείτε την . Η κάποιο λάθος στα δικά μου
Αν είναι αληθή τα παραπάνω τουλάχιστον δέχτηκαν σαν σωστό το "δεν γίνεται!" 8))
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 01:58:49 am
τι συνθηκες βρηκες? :)
Βρηκα τα gm, θm από ΓΤΡ και την θm=180+ <A(jωc) αρχικά για Κp=10 και Ki=40
και μου βγηκαν νορμαλ.
Στην επαληθευση με τη σχεση S(jω)<2 για τις τιμες αυτες των κερδων και στο διαγραμμα Bode κατι δεν παει καλα ομως :P
Εσυ τι έκανες ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 02:03:19 am
αα αλλιως το δουλεψα..
εκανα bode για την s
με τιμες που εδωσα και ειδα αν περναει το 20log2
εκανα bode για την s
με τιμες που εδωσα και ειδα αν περναει το 20log2
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: DoomGuard on January 28, 2013, 02:05:40 am
Αν είναι αληθή τα παραπάνω τουλάχιστον δέχτηκαν σαν σωστό το "δεν γίνεται!" 8))
Oh dear god.....
Κάτι άλλο, έχω παρατηρήσει ότι πολλά θέματα λύνονται και με απλά έναν Ι ελεγκτή(κ/s) αντί για PΙ.
Και τότε έχεις να προσδιορίσεις και λιγότερες σταθερές.
Ξέρουμε ότι η προσθήκη πόλου στο μηδέν χειροτερεύει κάπως την ευστάθεια,
ξέρει κανείς αν έχει ειπωθεί κάτι περί αυτού του θέματος στην αίθουσα?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 02:12:10 am
αα αλλιως το δουλεψα..
εκανα bode για την s
με τιμες που εδωσα και ειδα αν περναει το 20log2
εκανα bode για την s
με τιμες που εδωσα και ειδα αν περναει το 20log2
κι εγω το προσπάθησα αλλά κάπου κόλλησα.
Πως εκανες τον ελεγχο για την S(jω), θελω να πω, τι διαγραμμα Bode σου βγηκε ?
Δεν ειναι το ιδιο με το να κανουμε τον ελεγχο της A(jω) σε Bode και να σιγουρευτουμε οτι δεν
πεφτει κατω από 20log(0.5) ??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ValmadiaN on January 28, 2013, 02:15:57 am
Oh dear god.....
Κάτι άλλο, έχω παρατηρήσει ότι πολλά θέματα λύνονται και με απλά έναν Ι ελεγκτή(κ/s) αντί για PΙ.
Και τότε έχεις να προσδιορίσεις και λιγότερες σταθερές.
Ξέρουμε ότι η προσθήκη πόλου στο μηδέν χειροτερεύει κάπως την ευστάθεια,
ξέρει κανείς αν έχει ειπωθεί κάτι περί αυτού του θέματος στην αίθουσα?
Κάτι άλλο, έχω παρατηρήσει ότι πολλά θέματα λύνονται και με απλά έναν Ι ελεγκτή(κ/s) αντί για PΙ.
Και τότε έχεις να προσδιορίσεις και λιγότερες σταθερές.
Ξέρουμε ότι η προσθήκη πόλου στο μηδέν χειροτερεύει κάπως την ευστάθεια,
ξέρει κανείς αν έχει ειπωθεί κάτι περί αυτού του θέματος στην αίθουσα?
Η αλήθεια είναι ότι όντως κάποια προβλήματα λύνονται και με ολοκληρωτικό καθαρά ελεγκτή,
αλλά από τη στιγμή που δεν αναφέρεται κάτι τέτοιο στο βιβλίο δεν θα το τολμούσα!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Infinite Loop on January 28, 2013, 02:29:38 am
Δίκιο έχεις και εγώ προσπαθούσα ώρα να βγάλω άκρη αλλά δεν κατέληξα κάπου και το άφησα γιατί μου έτρωγε χρόνο.
Προσπάθησα μέχρι και να απαλείψω το μηδενικό στο 2..
Προσπάθησα μέχρι και να απαλείψω το μηδενικό στο 2..
Να κάτι που βρήκα σε παλαιότερο τόπικ. Για όσους παιδεύονται με το αντίστοιχο θέμα!
Το ζ και το ω ορίζονται για χαρακτηριστικά πολυώνυμα 2ου βαθμού. Πώς πήρες ότι 2ζω=9+κ ?
Απλά στη θεωρία κάνουμε μία επέκταση και λέμε ότι και για συστήματα μεγαλύτερου βαθμού απο 2 μπορούμε να προσεγγίσουμε τον χρόνο αποκατάστασης από τη θέση του κύριου πόλου ως ts=4.16/σ , όπου σ η θέση του κύριου πόλου στον αρνητικό πραγματικό άξονα.
Αν κάνει κανείς τον ΓΤΡ θα δεί ότι όπου και να τοποθετηθεί το μηδενικό c του PI ελεγκτή, το καλύτερο ts που μπορούμε να πετύχουμε είναι 4.16/2 = περίπου 2. Και αυτό για πολύ μεγάλες τιμές του κέρδους ώστε ο πόλος στο 0 να προσεγγίζει το μηδενικό στο -2.
Η προδιαγραφή αυτή με την ύλη των ΣΑΕ 1 είναι αδύνατη και έπεσε πολύ κράξιμο τον χειμώνα στον Πετρίδη. Τελικά βαθμολογήθηκαν με όλες τις μονάδες οι λύσεις που έλεγαν ότι είναι αδύνατη η ικανοποίησή της και το τεκμηρίωναν. Όσοι προσπάθησαν πατέντες με περίεργους ελεγκτές μπας και κάνουν τίποτα πήραν τα @@ τους.
Για το 4δ , αν και δεν το είχα πιάσει εκείνη την ώρα η σκέψη μου είναι η εξης:
Συνολικά η συνάρτησή μας έχει 2 μηδενικά και 3 πόλους. Για να βρούμε το περιθώριο φάσης , πρέπει να βρούμε τη συχνότητα ωc όπου το διάγραμμα bode κέρδους μηδενίζεται, δηλαδή θέτουμε το μέτρο της συνάρτησης ίσο με 1 , s=jωc, υψώνουμε στο τετράγωνο και λύνουμε ώς προς ωc. Επειδή έχω 3 πόλους, ο παρονομαστής θα μας δώσει όρο ω^6 , οπότε δε μπορούμε να λύσουμε αναλυτικά.
Αφού έχω την δυνατότητα επιλογής του ενός μηδενικου, δηλαδή του c=Ki/Kp , το παίρνω ίσο με 3 για να μου απαλείψει τον έναν πόλο. Έτσι η συνάρτησή μου προκύπτει:
Κp(s+2)/(s+3)(s+6)
Από το α) εύκολα βγάζω Ki>18 οπότε επιλέγω Ki=21, άρα kp=21/3=7 . Μπορεί να επιλέξει κανείς και διαφορετικό προφανώς. Με kp = 7 η παραπάνω διαδικασία μας δίνει ωc=4.19 Ηζ και περιθώριο φάσης 119 μοίρες που είναι αποδεκτό.
Τέλος για το γ) , απο ΓΤΡ μπορώ να δώ ότι το κέρδος μου είναι άπειρο. Αυτά.
Τώρα η απαλοιφή πόλου δε ξέρω κατά πόσο είναι πρακτικά καλη ιδέα, στα ΣΑΕ 2 είχε κάτι περίεργα που έλεγε ότι άλλες συναρτήσεις που θα προκύψουν σε άλλα προβλήματα μπορεί να είναι ασταθείς αλλα προφανώς δε μας νοιάζει. Δε ξέρω αν θα είχε πρόβλημα με αυτό ο πετρίδης , αλλά δε μπορώ να σκεφτώ άλλον τρόπο για να απαλαχθείς απο τις πράξεις για το δ.
Αν έχετε κάποια άλλη ιδέα παρακαλω μοιραστείτε την . Η κάποιο λάθος στα δικά μου
Αν είναι αληθή τα παραπάνω τουλάχιστον δέχτηκαν σαν σωστό το "δεν γίνεται!" 8))
Παρενθεση:
Οι τυποι που δινει ο Βασιλιας (ts = 4.16/σ, οπου σ το απολυτο πραγματικο μερος του δεξιοτερου πολου) ισχυουν ΜΟΝΟ σε συστηματα χωρις μηδενικα, και παλι προσεγγιστικα. Αν εχεις μηδενικα (και εδω εχεις δυο), ο ιδιος ο Βασιλιας παραδεχεται στο βιβλιο οτι αυτοι οι τυποι λειτουργουν μονο σαν "κατευθυντηριες γραμμες" - δηλαδη παιρνεις εναν (αρκετα) πιο συντηρητικο περιορισμο απο οτι πρεπει. Στην συγκεκριμενη περιπτωση, οντως με την μεθοδο του Βασιλια η προδιαγραφη για το ts δεν ικανοποιειται, αλλα αν βαλεις π.χ. kP = 50, kI = 200, οποτε το μηδενικο του ελεγκτη θα ειναι στο -4, παιρνεις (απο MATLAB):
esr = 0.045 (πληρουται)
ts = 0.482 (πληρουται)
Gm = inf (πληρουται)
φm = 93.4o (πληρουται).
Τωρα βεβαια ειναι να 'χαμε να λεγαμε... Το ηθικο διδαγμα ειναι οτι ο Τρολλιδης σου δινει τους τυπους για την περιπτωση που δεν εχεις μηδενικα, αλλα στην εξεταση παντα σου πεταει κανα δυο μηδενικα, και καμια φορα σου πεταει και καμια προδιαγραφη που ναι μεν δεν πληρουται, αλλα πληρουται, because fuck you students.
Αν είναι αληθή τα παραπάνω τουλάχιστον δέχτηκαν σαν σωστό το "δεν γίνεται!" 8))
Oh dear god.....
Κάτι άλλο, έχω παρατηρήσει ότι πολλά θέματα λύνονται και με απλά έναν Ι ελεγκτή(κ/s) αντί για PΙ.
Και τότε έχεις να προσδιορίσεις και λιγότερες σταθερές.
Ξέρουμε ότι η προσθήκη πόλου στο μηδέν χειροτερεύει κάπως την ευστάθεια,
ξέρει κανείς αν έχει ειπωθεί κάτι περί αυτού του θέματος στην αίθουσα?
ΠΑΝΤΑ βαζεις αναλογικο ορο. Ισχυει οτι με προσθηκη πολου στο 0 η σχετικη ευσταθεια χειροτερευει καπως, αλλα με προσεκτικη σχεδιαση δεν εχεις προβλημα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Infinite Loop on January 28, 2013, 06:38:58 am
τι συνθηκες βρηκες? :)
Βρηκα τα gm, θm από ΓΤΡ και την θm=180+ <A(jωc) αρχικά για Κp=10 και Ki=40
και μου βγηκαν νορμαλ.
Στην επαληθευση με τη σχεση S(jω)<2 για τις τιμες αυτες των κερδων και στο διαγραμμα Bode κατι δεν παει καλα ομως :P
Εσυ τι έκανες ?
Το κερδος βροχου βγαινει A(s) = 6kP(s+μ) / s(s+9), οπου μ = kI/kP. Η συναρτηση μεταφορας ευαισθησιας ειναι S(s) = 1 / (1+A(s)) = s(s+9) / (s2 + (6kP+9)s + 6kI). Προφανως, για ω->inf, |S(jω)|->1, αρα για οποιεσδηποτε τιμες του kP και kI η συνθηκη |S(jω)|<=2, για καθε ω, δεν επαληθευεται. Ομως αυτη η συνθηκη ειναι ικανη για να ειναι Gm>=2 και φm>=30o, και οχι αναγκαια, και πραγματι για kP=kI=20 ειναι Gm=inf, φm=93.8o. Αρα εδω θα ηθελε λογικα να του πεις οτι η συνθηκη ειναι ικανη και οχι αναγκαια.
Edit: εκανα λαθος απο βιασυνη, βλεπε επομενο ποστ
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: johnnykost on January 28, 2013, 10:25:40 am
Έίναι το περσινό θέμα σχεδίασης:
Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
Για το gm>2 δεν μπορούμε να πούμε ko/k>2 ?Δινεται το σύστημα Hp(s)=6/(s+9)
Να σχεδιασθεί σύστημα ελέγχου κλειστού βρόχου με μοναδιαία αρνητική ανάδραση που να ικανοποιεί τις προδιαγραφές :
1) ess = 0
2) esr το πολύ 0.1
3) ωb τουλάχιστον 30rad/s
4) gm > 2
5) θm > 30
Να ελεγχθεί η ικανοποίηση των προδιαγραφών (4) και (5) χρησιμοποιώντας τη συνάρτηση μεταφοράς ευαισθησίας.
εδιτ: άκυρο τώρα έιδα πως ζητάει να χρησιμοποιήσουμε συνάρτηση μεταφοράς ευαισθησίας
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: john-john on January 28, 2013, 11:30:42 am
Μπορει καποιος να εξηγξσει τι παιζει με την συναρτηση μεταφορας ευαοσθησιας?
Σχετικα με το πανω θεμα ας πουμε.
Ευχαριστω εκ των προτερων
Σχετικα με το πανω θεμα ας πουμε.
Ευχαριστω εκ των προτερων
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: teslaaaa on January 28, 2013, 11:44:31 am
τι συνθηκες βρηκες? :)
Βρηκα τα gm, θm από ΓΤΡ και την θm=180+ <A(jωc) αρχικά για Κp=10 και Ki=40
και μου βγηκαν νορμαλ.
Στην επαληθευση με τη σχεση S(jω)<2 για τις τιμες αυτες των κερδων και στο διαγραμμα Bode κατι δεν παει καλα ομως :P
Εσυ τι έκανες ?
Το κερδος βροχου βγαινει A(s) = 6kP(s+μ) / s(s+9), οπου μ = kI/kP. Η συναρτηση μεταφορας ευαισθησιας ειναι S(s) = 1 / (1+A(s)) = s(s+9) / (s2 + (6kP+9)s + 6kI). Προφανως, για ω->inf, |S(jω)|->1, αρα για οποιεσδηποτε τιμες του kP και kI η συνθηκη |S(jω)|<=2, για καθε ω, δεν επαληθευεται. Ομως αυτη η συνθηκη ειναι ικανη για να ειναι Gm>=2 και φm>=30o, και οχι αναγκαια, και πραγματι για kP=kI=20 ειναι Gm=inf, φm=93.8o. Αρα εδω θα ηθελε λογικα να του πεις οτι η συνθηκη ειναι ικανη και οχι αναγκαια.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ναταλία on January 28, 2013, 12:00:05 pm
τι συνθηκες βρηκες? :)
Βρηκα τα gm, θm από ΓΤΡ και την θm=180+ <A(jωc) αρχικά για Κp=10 και Ki=40
και μου βγηκαν νορμαλ.
Στην επαληθευση με τη σχεση S(jω)<2 για τις τιμες αυτες των κερδων και στο διαγραμμα Bode κατι δεν παει καλα ομως :P
Εσυ τι έκανες ?
Το κερδος βροχου βγαινει A(s) = 6kP(s+μ) / s(s+9), οπου μ = kI/kP. Η συναρτηση μεταφορας ευαισθησιας ειναι S(s) = 1 / (1+A(s)) = s(s+9) / (s2 + (6kP+9)s + 6kI). Προφανως, για ω->inf, |S(jω)|->1, αρα για οποιεσδηποτε τιμες του kP και kI η συνθηκη |S(jω)|<=2, για καθε ω, δεν επαληθευεται. Ομως αυτη η συνθηκη ειναι ικανη για να ειναι Gm>=2 και φm>=30o, και οχι αναγκαια, και πραγματι για kP=kI=20 ειναι Gm=inf, φm=93.8o. Αρα εδω θα ηθελε λογικα να του πεις οτι η συνθηκη ειναι ικανη και οχι αναγκαια.
γιατι δεν επαληθευεται??
αφου λες οτι για μεγαλα ω η S τεινει στο 1, και συ την θες μικροτερη του 2!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 13:12:11 pm
Το κερδος βροχου βγαινει A(s) = 6kP(s+μ) / s(s+9), οπου μ = kI/kP. Η συναρτηση μεταφορας ευαισθησιας ειναι S(s) = 1 / (1+A(s)) = s(s+9) / (s2 + (6kP+9)s + 6kI). Προφανως, για ω->inf, |S(jω)|->1, αρα για οποιεσδηποτε τιμες του kP και kI η συνθηκη |S(jω)|<=2, για καθε ω, δεν επαληθευεται. Ομως αυτη η συνθηκη ειναι ικανη για να ειναι Gm>=2 και φm>=30o, και οχι αναγκαια, και πραγματι για kP=kI=20 ειναι Gm=inf, φm=93.8o. Αρα εδω θα ηθελε λογικα να του πεις οτι η συνθηκη ειναι ικανη και οχι αναγκαια.
Συμφωνώ με τα gm, θm και με το limS(jω)->1 για ω->inf.
Είναι αρκετό όμως αυτό? Δε μπορεί η S(jω) να παίρνει κάποια τιμή >2 ενδιάμεσα ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Infinite Loop on January 28, 2013, 13:52:23 pm
Το κερδος βροχου βγαινει A(s) = 6kP(s+μ) / s(s+9), οπου μ = kI/kP. Η συναρτηση μεταφορας ευαισθησιας ειναι S(s) = 1 / (1+A(s)) = s(s+9) / (s2 + (6kP+9)s + 6kI). Προφανως, για ω->inf, |S(jω)|->1, αρα για οποιεσδηποτε τιμες του kP και kI η συνθηκη |S(jω)|<=2, για καθε ω, δεν επαληθευεται. Ομως αυτη η συνθηκη ειναι ικανη για να ειναι Gm>=2 και φm>=30o, και οχι αναγκαια, και πραγματι για kP=kI=20 ειναι Gm=inf, φm=93.8o. Αρα εδω θα ηθελε λογικα να του πεις οτι η συνθηκη ειναι ικανη και οχι αναγκαια.
Συμφωνώ με τα gm, θm και με το limS(jω)->1 για ω->inf.
Είναι αρκετό όμως αυτό? Δε μπορεί η S(jω) να παίρνει κάποια τιμή >2 ενδιάμεσα ?
Εχεις δικιο, εγω μπερδευτηκα (δεν ειχα πιει και καφε εκεινη την ωρα), και νομισα οτι η συνθηκη ηταν |S(jω)|<=1/2. Τεσπα, στην συγκεκριμενη περιπτωση ειναι προφανες (αμα κανεις και Bode φαινεται ευκολα) οτι η |S(jω)| ειναι αυξουσα συναρτηση του ω, αρα αφου το supremum της ειναι το 1, θα ισχυει |S(jω)|<1 και αρα |S(jω)|<=2, για καθε ω. Σε αλλη περιπτωση δεν θα ητανε τοσο απλο, και θα επρεπε να κανεις Bode.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Επικο Burger on January 28, 2013, 14:19:16 pm
τι συνθηκες βρηκες? :)
Βρηκα τα gm, θm από ΓΤΡ και την θm=180+ <A(jωc) αρχικά για Κp=10 και Ki=40
και μου βγηκαν νορμαλ.
Στην επαληθευση με τη σχεση S(jω)<2 για τις τιμες αυτες των κερδων και στο διαγραμμα Bode κατι δεν παει καλα ομως :P
Εσυ τι έκανες ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kostas89 on January 28, 2013, 14:21:04 pm
Θέμα 1 Ιουνίου 2007
Το συνολικό σφάλμα θέσης και ταχύτητας πως τα βρίσκουμε..?
Θα είναι Ε=r[1-Hk] ..? όπου Hk θα περιλαμβάνει και την ΣΜ του D?
Το συνολικό σφάλμα θέσης και ταχύτητας πως τα βρίσκουμε..?
Θα είναι Ε=r[1-Hk] ..? όπου Hk θα περιλαμβάνει και την ΣΜ του D?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: antonios on January 28, 2013, 14:23:36 pm
Θέμα 1 Ιουνίου 2007
Το συνολικό σφάλμα θέσης και ταχύτητας πως τα βρίσκουμε..?
Το συνολικό σφάλμα θέσης και ταχύτητας πως τα βρίσκουμε..?
σαν να είσαι λίγο αδιάβαστος..... :???:
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 14:29:28 pm
Ρε παιδια σ'αυτο σας βγαινει σωστα και το ωb? Η εγω κανω καμια μαλακια την οποια απλα τωρα δεν μπορω να δω?
Η συνθήκη |A(j30)|>1 (για να εχεις ωb>ωc>30rad/s) μου δίνει εναν περιορισμό για το κέρδος Kp.
Έχω επιλέξει το μηδενικό του ελεγκτή φυσικά. Σε ποιο κομμάτι αναφέρεσαι ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Επικο Burger on January 28, 2013, 14:40:40 pm
Ρε παιδια σ'αυτο σας βγαινει σωστα και το ωb? Η εγω κανω καμια μαλακια την οποια απλα τωρα δεν μπορω να δω?
Η συνθήκη |A(j30)|>1 (για να εχεις ωb>ωc>30rad/s) μου δίνει εναν περιορισμό για το κέρδος Kp.
Έχω επιλέξει το μηδενικό του ελεγκτή φυσικά. Σε ποιο κομμάτι αναφέρεσαι ?
Ναι σ'αυτο, οκ παιρνω την συνθηκη αυτη και καταληγω και εγω σε μια σχεση για το Κp. Αλλα οταν το βαζω στο matlab δεν μου βγαινει το σωστο Bandwith! Για την ακριβεια μ βγαινει πολυ μικρο! Και ψαχνω να βρω τι λαθος εχω αλλα δεν μπορω :(
Υ.Γ. η σχεση που εχω για το Κp , με μηδενικο στο 3, ειναι Κp>=5
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 14:44:40 pm
Ρε παιδια σ'αυτο σας βγαινει σωστα και το ωb? Η εγω κανω καμια μαλακια την οποια απλα τωρα δεν μπορω να δω?
Η συνθήκη |A(j30)|>1 (για να εχεις ωb>ωc>30rad/s) μου δίνει εναν περιορισμό για το κέρδος Kp.
Έχω επιλέξει το μηδενικό του ελεγκτή φυσικά. Σε ποιο κομμάτι αναφέρεσαι ?
Ναι σ'αυτο, οκ παιρνω την συνθηκη αυτη και καταληγω και εγω σε μια σχεση για το Κp. Αλλα οταν το βαζω στο matlab δεν μου βγαινει το σωστο Bandwith! Για την ακριβεια μ βγαινει πολυ μικρο! Και ψαχνω να βρω τι λαθος εχω αλλα δεν μπορω :(
Υ.Γ. η σχεση που εχω για το Κp , με μηδενικο στο 3, ειναι Κp>=5
Nαι κι εμένα Kp>=5 μου δίνει και μετά παίρνω ωc~60rad/s.. Λάθος του matlab μάλλον :P :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Επικο Burger on January 28, 2013, 14:47:31 pm
Ρε παιδια σ'αυτο σας βγαινει σωστα και το ωb? Η εγω κανω καμια μαλακια την οποια απλα τωρα δεν μπορω να δω?
Η συνθήκη |A(j30)|>1 (για να εχεις ωb>ωc>30rad/s) μου δίνει εναν περιορισμό για το κέρδος Kp.
Έχω επιλέξει το μηδενικό του ελεγκτή φυσικά. Σε ποιο κομμάτι αναφέρεσαι ?
Ναι σ'αυτο, οκ παιρνω την συνθηκη αυτη και καταληγω και εγω σε μια σχεση για το Κp. Αλλα οταν το βαζω στο matlab δεν μου βγαινει το σωστο Bandwith! Για την ακριβεια μ βγαινει πολυ μικρο! Και ψαχνω να βρω τι λαθος εχω αλλα δεν μπορω :(
Υ.Γ. η σχεση που εχω για το Κp , με μηδενικο στο 3, ειναι Κp>=5
Nαι κι εμένα Kp>=5 μου δίνει και μετά παίρνω ωc~60rad/s.. Λάθος του matlab μάλλον :P :P
Στα ιδια ειμαστε λοιπον, παντως το matlab δυσκολα να κανει λαθος :P
Το εβαλες και εσυ matlab?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aloko on January 28, 2013, 14:54:57 pm
Ρε παιδια σ'αυτο σας βγαινει σωστα και το ωb? Η εγω κανω καμια μαλακια την οποια απλα τωρα δεν μπορω να δω?
Η συνθήκη |A(j30)|>1 (για να εχεις ωb>ωc>30rad/s) μου δίνει εναν περιορισμό για το κέρδος Kp.
Έχω επιλέξει το μηδενικό του ελεγκτή φυσικά. Σε ποιο κομμάτι αναφέρεσαι ?
Ναι σ'αυτο, οκ παιρνω την συνθηκη αυτη και καταληγω και εγω σε μια σχεση για το Κp. Αλλα οταν το βαζω στο matlab δεν μου βγαινει το σωστο Bandwith! Για την ακριβεια μ βγαινει πολυ μικρο! Και ψαχνω να βρω τι λαθος εχω αλλα δεν μπορω :(
Υ.Γ. η σχεση που εχω για το Κp , με μηδενικο στο 3, ειναι Κp>=5
Nαι κι εμένα Kp>=5 μου δίνει και μετά παίρνω ωc~60rad/s.. Λάθος του matlab μάλλον :P :P
Στα ιδια ειμαστε λοιπον, παντως το matlab δυσκολα να κανει λαθος :P
Το εβαλες και εσυ matlab?
Το matlab δεν κάνει λάθος αυτό είναι σίγουρο :P
Δεν έχω για να το τρέξω κι εγώ και να συγκρίνουμε, πάντως ο συλλογισμός φαίνεται σωστός..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: FireStarter on June 18, 2013, 19:22:19 pm
Έχω μια απορία σχετικά με τα θέματα της πτυχιακής του 2010. Όπως λένε κάποιοι στην σελίδα 2 του topic σχετικά με το 1ο θέμα, η συνάρτηση μεταφοράς ανοιχτού βρόχου θα ληφθεί ίση με το γινόμενο της δοσμένης συνάρτησης μεταφοράς επί την συνάρτηση μεταφοράς της ανάδρασης (δείτε και το σχήμα).
Μπορεί να μου εξηγήσει κάποιος γιατί συμβαίνει αυτό;
Μπορεί να μου εξηγήσει κάποιος γιατί συμβαίνει αυτό;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: leroy on August 28, 2013, 12:32:46 pm
Έχει κανείς τα θέματα Σεπτεμβρίου 2011?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ForestBlack on August 28, 2013, 19:21:22 pm
Σεπτέμβριος 2012
Θέμα1
Βρίσκει κανένας άλλος ω1=4,9946 ω2=20.0216 ωb=141.253 ?
επίσης αυτά τα στρογγυλοποιώ ή τα αφήνω έτσι;
Θέμα1
Βρίσκει κανένας άλλος ω1=4,9946 ω2=20.0216 ωb=141.253 ?
επίσης αυτά τα στρογγυλοποιώ ή τα αφήνω έτσι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: MARIOS on August 30, 2013, 14:11:21 pm
Λοιπόν... να κάνω μια ερώτηση εδώ μιας και είναι στα recent....Λοιπόν για το Gm , θm ...
Το Gm=1/Am .... .το Am το βρίσκω από την εξίσωση Α(s)=0?
και για την θm... το ωc το βρίσκω |Α(jωc)|=0 έτσι??? (Βασικά αυτό εντάξει είναι λίγο ξεκάθαρο νομίζω αλλά το Gm με μπερδεύει)
Το Gm=1/Am .... .το Am το βρίσκω από την εξίσωση Α(s)=0?
και για την θm... το ωc το βρίσκω |Α(jωc)|=0 έτσι??? (Βασικά αυτό εντάξει είναι λίγο ξεκάθαρο νομίζω αλλά το Gm με μπερδεύει)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on August 30, 2013, 14:20:20 pm
σελ 367-371.
και το 2ο που ρωτας ειναι λαθος. |Α(jωc)|=1 δηλαδη |Α(jωc)|Db=0
και το 2ο που ρωτας ειναι λαθος. |Α(jωc)|=1 δηλαδη |Α(jωc)|Db=0
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: MARIOS on August 30, 2013, 14:22:51 pm
ΩΩΩ ναι.... μλκ μου.... δεν πρόλαβα να γυρίσω την σελίδα για να το δω.... τα έχω και σημειωμένα στο σχήμα στην 370 πανάθεμά με.... thanks πάντως...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: choco18 on August 31, 2013, 21:23:31 pm
σεπτε΄μβριος 2012, 1ο θέμα:
τα ω1,ω2 τα βρήκα και εγώ τόσο αλλά το ωb=196.34! πως το δούλεψες;
τα ω1,ω2 τα βρήκα και εγώ τόσο αλλά το ωb=196.34! πως το δούλεψες;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on August 31, 2013, 23:07:24 pm
Θεμα 1 Σεπτ 2009
απο τα λυμμενα
αν διαλεξουμε για α>3.3 διαλεξουμε α=4 για να διωξουμε ενα μηδενικο λετε να στραβωσουν? Το λεω γιατι ψιλοφωναζει με την τριτοβαθμια που βγαινει μετα.
απο τα λυμμενα
αν διαλεξουμε για α>3.3 διαλεξουμε α=4 για να διωξουμε ενα μηδενικο λετε να στραβωσουν? Το λεω γιατι ψιλοφωναζει με την τριτοβαθμια που βγαινει μετα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 01, 2013, 14:46:35 pm
τελικα παιδια οταν λεει στις προδιαγραφες οτι θελει πχ απορριψη διαταραχων τουλαχιστον 20 dB, θα βαζω μικροτερο η ισο του 20 η του -20? γιατι καποια παιδια στο φορουμ λενε να βαζουμε -20..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Nerevar on September 01, 2013, 14:50:03 pm
τελικα παιδια οταν λεει στις προδιαγραφες οτι θελει πχ απορριψη διαταραχων τουλαχιστον 20 dB, θα βαζω μικροτερο η ισο του 20 η του -20? γιατι καποια παιδια στο φορουμ λενε να βαζουμε -20..
Θελεις |Ηyd|<= - 20db,για το θορυβο δε θυμαμαι.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Elade on September 01, 2013, 15:06:06 pm
στο 2ο θέμα του 2013, τον χρόμο αποκατάστασης τον βγάζουμε απο τον τύπο σ>=4.16/α ή απο αυτό που λέει εδώ ο gate4?
Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 01, 2013, 15:19:30 pm
στο 2ο θέμα του 2013, τον χρόμο αποκατάστασης τον βγάζουμε απο τον τύπο σ>=4.16/α ή απο αυτό που λέει εδώ ο gate4?
φανταζομαι αυτο θα το χρησιμοποιησεις στο τελος για επαληθευση Otan leei ts< apo kati, isxyei ts=4.16/σ το σ brisketai apo ton paronomasth ths Hk analoga ti morfh exei.An einai prwtoy bathmou το σ einai iso me ton polo,2ou kai tritou bathmou iso me ton sintelesti toy s kai s^2 dia 2 antistoixa...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on September 01, 2013, 15:21:43 pm
Οχι ρε γιατι δεν βγαινει? το -σ<=-5.94. αρα ολοι οι πολοι πρεπει να ναι αριστεροτερα που ισχυει. Εχεις ασυμπτωτες 90 και -90 και πας για ΟΑ αριστεροτερα του -5.94 ετσι ωστε να τηρειται η προδιαγραφη για ολα τα κ και βρισκεις ετσι και το μ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Elade on September 01, 2013, 15:23:13 pm
Οχι ρε γιατι δεν βγαινει? το -σ<=-5.94. αρα ολοι οι πολοι πρεπει να ναι αριστεροτερα συνεχεια. Εχεις ασυμπτωτες 90 και -90 και πας για ΟΑ αριστεροτερα του 5.94 ετσι ωστε να τηρειται η προδιαγραφη για ολα τα κ και βρισκεις ετσι και το μ.
έκανα διορθωση, είχα κάνει μαλακια στις πράξεις :P, ευχαριστώ για τις απαντήσεις πάντωςTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 01, 2013, 15:37:28 pm
τοτε να ρωτησω εγω κατι..! Οταν βρισκω το κ στην σχεδιαση και ελεγχω αν πληρουνται τα κριτηρια μου, το χρονο αποκαταστασης πως τον ελεγχω αν ειναι σωστος?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on September 01, 2013, 15:39:27 pm
Μπορει καποιος να μου εξηγησει τι παιζει με τις διαταραχες και τον θορυβο? Ξερω οτι στο βιβλιο λεει αυτο που λεει αλλα σε μενα γιατι βγαζει νοημα το αντιστροφο? Δλδ αν θες να μην εχεις διαταραχες δεν ειναι πιο λογικο να χεις |Ηyd| μεγαλο στις χαμηλες συχνοτητες που ουτως ή αλλως δεν εχεις θορυβο? Και Μεγαλο |Ηyn| για τις υψηλες συχνοτητες που ετσι και αλλιως δεν εχεις διαταραχες?? Τι μου διαφευγει?
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Elade on September 01, 2013, 15:41:38 pm
τοτε να ρωτησω εγω κατι..! Οταν βρισκω το κ στην σχεδιαση και ελεγχω αν πληρουνται τα κριτηρια μου, το χρονο αποκαταστασης πως τον ελεγχω αν ειναι σωστος?
αν δεν κάνω λάθος, με τους τύπους που εφαρμόζουμε ο χρόνος αποκατάστασης δεν επηρρεάζεται απ το κTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 01, 2013, 15:43:16 pm
τοτε να ρωτησω εγω κατι..! Οταν βρισκω το κ στην σχεδιαση και ελεγχω αν πληρουνται τα κριτηρια μου, το χρονο αποκαταστασης πως τον ελεγχω αν ειναι σωστος?
αν δεν κάνω λάθος, με τους τύπους που εφαρμόζουμε ο χρόνος αποκατάστασης δεν επηρρεάζεται απ το κTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Nerevar on September 01, 2013, 15:47:48 pm
Μπορει καποιος να μου εξηγησει τι παιζει με τις διαταραχες και τον θορυβο? Ξερω οτι στο βιβλιο λεει αυτο που λεει αλλα σε μενα γιατι βγαζει νοημα το αντιστροφο? Δλδ αν θες να μην εχεις διαταραχες δεν ειναι πιο λογικο να χεις |Ηyd| μεγαλο στις χαμηλες συχνοτητες που ουτως ή αλλως δεν εχεις θορυβο? Και Μεγαλο |Ηyn| για τις υψηλες συχνοτητες που ετσι και αλλιως δεν εχεις διαταραχες?? Τι μου διαφευγει?
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Ξεχνας οτι το μετρο της συναρτησης μεταφορας σε μια συγκεκριμενη συχνοτητα ειναι καποιο ειδος κερδους,πχ αν εχεις |Ηyd|>1 (οχι σε db),εστω 2,τοτε εχεις ενισχυση των διαταραχων στην εξοδο.Αυτο που θελεις ειναι αποσβεση/απορριψη διαταραχων/θορυβου ωστε να μην ειναι πιο ισχυρες στην εξοδο,δηλαδη |Ηyd|<<1/|Ηyn|<<1 (και αν το μετατρεψεις σε db βγαινει αρνητικος αριθμος,πχ -20) στις συχνοτητες που σε ενδιαφερουν.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Elade on September 01, 2013, 15:48:04 pm
τοτε να ρωτησω εγω κατι..! Οταν βρισκω το κ στην σχεδιαση και ελεγχω αν πληρουνται τα κριτηρια μου, το χρονο αποκαταστασης πως τον ελεγχω αν ειναι σωστος?
αν δεν κάνω λάθος, με τους τύπους που εφαρμόζουμε ο χρόνος αποκατάστασης δεν επηρρεάζεται απ το κTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on September 01, 2013, 15:53:10 pm
Μπορει καποιος να μου εξηγησει τι παιζει με τις διαταραχες και τον θορυβο? Ξερω οτι στο βιβλιο λεει αυτο που λεει αλλα σε μενα γιατι βγαζει νοημα το αντιστροφο? Δλδ αν θες να μην εχεις διαταραχες δεν ειναι πιο λογικο να χεις |Ηyd| μεγαλο στις χαμηλες συχνοτητες που ουτως ή αλλως δεν εχεις θορυβο? Και Μεγαλο |Ηyn| για τις υψηλες συχνοτητες που ετσι και αλλιως δεν εχεις διαταραχες?? Τι μου διαφευγει?
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Συμφωνα με αυτα που λεει το βιβλιο για το θεμα 2013 για τον θορυβο παιρνω |Ηyn|<-10dB => (A(s))/(1+A(s))<-10dB =>A(s)<-10dB??
Ξεχνας οτι το μετρο της συναρτησης μεταφορας σε μια συγκεκριμενη συχνοτητα ειναι καποιο ειδος κερδους,πχ αν εχεις |Ηyd|>1 (οχι σε db),εστω 2,τοτε εχεις ενισχυση των διαταραχων στην εξοδο.Αυτο που θελεις ειναι αποσβεση/απορριψη διαταραχων/θορυβου ωστε να μην ειναι πιο ισχυρες στην εξοδο,δηλαδη |Ηyd|<<1/|Ηyn|<<1 (και αν το μετατρεψεις σε db βγαινει αρνητικος αριθμος,πχ -20) στις συχνοτητες που σε ενδιαφερουν.
Εδιτ: τωρα που το σκεφτομαι το |Hyd| προστιθεται στην εξοδο και δεν ειναι SNR. THanx.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 01, 2013, 17:58:18 pm
στο θεμα 1 του 11 τι ελεγκτη χρησιμοποιησατε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: nastia on September 01, 2013, 21:36:38 pm
Μπορεί κάποιος με 2 λόγια να μου εξηγήσει πως κάνουμε διάγραμμα Bode?
π.χ στο θέμα 3 του Ιανουαρίου του '11!
Κάπου κολλάω στη λογική και μου βγαίνουν λάθος!
π.χ στο θέμα 3 του Ιανουαρίου του '11!
Κάπου κολλάω στη λογική και μου βγαίνουν λάθος!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: BabylonX on September 01, 2013, 23:05:01 pm
Ο Γενάρης του 11 δεν έχει 3ο θέμα.
Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 02, 2013, 00:15:31 am
Ο Γενάρης του 11 δεν έχει 3ο θέμα.
Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
ε καλα δεν ειναι λιγο τραβηγμενο να ζητησει διαγραμμα bode φασης? ειναι πολυ πιο περιπλοκο απο του κερδους..Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
δεν εχω δει και κανενα παλιο θεμα που να ζηταει..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: rainmaker on September 02, 2013, 00:21:27 am
λαθος:)στα θεματα που συζητουσαμε μαζι με τους δυο ελεγκτες,στο 1ο θεμα ζητουσε διαγραμμα φασεων.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 02, 2013, 00:27:42 am
λαθος:)στα θεματα που συζητουσαμε μαζι με τους δυο ελεγκτες,στο 1ο θεμα ζητουσε διαγραμμα φασεων.
διαφωνω αγορινα.. ζητουσε bode κερδους και στο 2ο που ζητουσε περιθωριο φασης εβγαινε ανετα χωρις το διαγραμμα φασης :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: rainmaker on September 02, 2013, 00:35:54 am
ωπ sorry λαθος μου.παντως το χα δει να ζητειται σε κατι λυμενα ισως να ταν και υπερβολικα παλια:):)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 02, 2013, 00:37:08 am
ωπ sorry λαθος μου.παντως το χα δει να ζητειται σε κατι λυμενα ισως να ταν και υπερβολικα παλια:):)
ελπιζω πανω πανω στην κολλα να γραφε ΚΑΕ γιατι αλλιως την πατησαμε..!! :DTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 02, 2013, 00:39:31 am
να ρωτησω εγω κατι πανω στα bode παντως.. Οταν μας λεει προσεγγιστικα εννοει απλα πως θα ειναι περιπου? η θα πρεπει να υπολογισουμε και πχ τι H θα εχουμε σε καθε αλλαγη της κλισης της καμπυλης καθως επιδρουν οι πολοι και τα μηδενικα..?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: varvoutis on September 02, 2013, 01:21:36 am
ωπ sorry λαθος μου.παντως το χα δει να ζητειται σε κατι λυμενα ισως να ταν και υπερβολικα παλια:):)
ελπιζω πανω πανω στην κολλα να γραφε ΚΑΕ γιατι αλλιως την πατησαμε..!! :Dρε παιδιά, άσχετο, αλλά τι σημαίνει ΚΑΕ? Τα Α και Ε υποθέτω πως είναι Αυτομάτου Ελέγχου, το Κ όμως τι είναι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: saddodancererer on September 02, 2013, 01:23:24 am
νομιζω οτι το Κ βγαινει απο την μεταβλητη που υπολογιζουμε σε ολες τις ασκησεις..! :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on September 02, 2013, 01:35:50 am
ωπ sorry λαθος μου.παντως το χα δει να ζητειται σε κατι λυμενα ισως να ταν και υπερβολικα παλια:):)
ελπιζω πανω πανω στην κολλα να γραφε ΚΑΕ γιατι αλλιως την πατησαμε..!! :Dρε παιδιά, άσχετο, αλλά τι σημαίνει ΚΑΕ? Τα Α και Ε υποθέτω πως είναι Αυτομάτου Ελέγχου, το Κ όμως τι είναι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: nikosmp on September 02, 2013, 10:45:08 am
Σεπτέμβριος 2012
Θέμα1
Βρίσκει κανένας άλλος ω1=4,9946 ω2=20.0216 ωb=141.253 ?
επίσης αυτά τα στρογγυλοποιώ ή τα αφήνω έτσι;
Θέμα1
Βρίσκει κανένας άλλος ω1=4,9946 ω2=20.0216 ωb=141.253 ?
επίσης αυτά τα στρογγυλοποιώ ή τα αφήνω έτσι;
Μπορεί κάποιος να εξηγήσει πώς προκύπτουν τα ω1 ω2;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: nastia on September 02, 2013, 10:48:23 am
Ο Γενάρης του 11 δεν έχει 3ο θέμα.
Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
Γενικά η λογική είναι να σπάσεις τη συνάρτησή σου σε παράγοντες της μορφής H0, H1, H2 (σελ 215), να βγάλεις τα bode για κάθε μία από αυτές (σελ 219 με 224 ακολουθείς τις προσεγγιστικές οδηγίες) και στο τέλος προσθέτεις αλγεβρικά όλα τα bode κέρδους και παίρνεις το τελικό bode κέρδους και όλα τα bode φάσης και παίρνεις το τελικό bode φάσης.
Τώρα γενικά αν δεν έχεις μιγαδικούς πόλους και μηδενικά είναι αρκετά εύκολο και φαίνεται στο παράδειγμα 5.2.1 σελ 226.
Μια γραμμή οριζόντια για το σταθερό κέρδος 5 και μετά γραμμές με κλίσεις 20db/δεκάδα για τα μηδενικά και -20db/δεκάδα για τους πόλους. Τις προσθέτεις όλες αλγεβρικά και παίρνεις το bode κέρδους. Για το bode φάσης παίρνεις κάθε πόλο και μηδενικό και κάνεις το εξής:
Εστω μηδενικό στο 5 οπως λέει το παραδειγμα:
Μεταξύ 0 και 0.5 (ένα δέκατο του 5) δίνει 0 μοίρες
Από το 50 (δεκαπλάσιο του 5) και πάνω 90 μοίρες
Στο ενδιάμεσο γραμμική ώστε στο 5 να πέφτουμε στις 45 μοίρες
Στους πόλους το αντιμετωπίζεις το ίδιο αλλά παίρνεις γωνίες 0, -45 και -90.
Ετσι με ένα σμπάρο βγάζεις bode για H0 και Η1 μαζί. Απλά προσέχεις κάπως περισσότερο αν έχεις πόλους και μηδενικά στο 0 γιατί για το bode κέρδους δεν αλλάζει κάτι (εκεί κανονικά προσθέτεις ή αφαιρείς κλίσεις 20db/δεκάδα ξεκινώντας από το 0) αλλά στα φάσης αφαιρείς π/2 για κάθε πόλο ή προσθέτεις π/2 για κάθε μηδενικό. Εάν έχεις και τίποτα συζυγείς μιγαδικούς πόλους, τους βγάζεις κοινό παράγοντα, τους δουλεύεις ξεχωριστά όπως περιγράφει στις σελίδες 222 με 224 και προσθέτεις τα αποτελέσματα στο παραπάνω.
Με ξεμπέρδεψες αρκετά!ευχαριστώ!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: mar-m on January 16, 2014, 17:42:56 pm
Καμιά ιδέα για το 2ο θέμα του Σεπτέμβρη 2013? :-[
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mr K on January 23, 2014, 16:55:59 pm
Παιδιά Σεπτέμβριος 2013 θέμα α ερώτημα β λέει:
(Αφού έχουμε σχεδιάσει τον ΓΤΡ), να βρεθεί το περιθώριο κέρδους του ΣΚΒ με μοναδιαία αρνητική ανάδραση. Καμία ιδέα; δεν θα έπρεπε να λέει για συγκεκριμένο κ; Αλλιώς το περιθώριο μεταβάλλεται για κάθε κ.
(Αφού έχουμε σχεδιάσει τον ΓΤΡ), να βρεθεί το περιθώριο κέρδους του ΣΚΒ με μοναδιαία αρνητική ανάδραση. Καμία ιδέα; δεν θα έπρεπε να λέει για συγκεκριμένο κ; Αλλιώς το περιθώριο μεταβάλλεται για κάθε κ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Grecs on January 23, 2014, 17:13:00 pm
Bασικα ζηταει να βρεις το κ και αν θυμαμαι καλα θελει Routh
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mr K on January 23, 2014, 18:05:27 pm
Bασικα ζηταει να βρεις το κ και αν θυμαμαι καλα θελει Routh
Ναι βασικα ειναι Κ/Κο οπου Κο το οριακο κ για ευστάθεια ενω το κ για ωc ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 23, 2014, 19:19:08 pm
Γενικά στα παλιά θέματα όταν ζητείτα διάγραμμα Bode η σχεδιάση είναι προσεγγιστική;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 23, 2014, 19:59:50 pm
Γενικά στα παλιά θέματα όταν ζητείτα διάγραμμα Bode η σχεδιάση είναι προσεγγιστική;
Τι εννοείς προσεγγιστική; Γενικά το διάγραμμα Bode είναι προσέγγιση της γραφικής παράστασης πλάτους/φάσης μια συνάρτησης μεταφοράς.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 23, 2014, 20:10:57 pm
Τι εννοείς προσεγγιστική; Γενικά το διάγραμμα Bode είναι προσέγγιση της γραφικής παράστασης πλάτους/φάσης μια συνάρτησης μεταφοράς.
Ποια από τις δύο; :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 23, 2014, 20:18:19 pm
Τι εννοείς προσεγγιστική; Γενικά το διάγραμμα Bode είναι προσέγγιση της γραφικής παράστασης πλάτους/φάσης μια συνάρτησης μεταφοράς.
Ποια από τις δύο; :)
Τη δεύτερη μέθοδο χρησιμοποιούμε, δε νομίζω πως θα ζητηθεί να βάζουμε τιμές στο ω για να κάνουμε τη γραφική παράσταση.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 23, 2014, 20:23:59 pm
Ευχαριστώ!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 25, 2014, 20:19:18 pm
Οταν εχει προδιαγραφει για χρονο ανοδο (πχ ts<0.7) , μπορω να παω απο τον τυπο που λεει στο βιβλιο οτι ισχυει (προσεγγιστικα) σ>4.16/0.7 αν το συστημα ειναι δευτερου βαθμου, σωστα?
Αν ειναι μεγαλυτερου τι κανω? :-\
Αν ειναι μεγαλυτερου τι κανω? :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 25, 2014, 20:37:37 pm
Οταν εχει προδιαγραφει για χρονο ανοδο (πχ ts<0.7) , μπορω να παω απο τον τυπο που λεει στο βιβλιο οτι ισχυει (προσεγγιστικα) σ>4.16/0.7 αν το συστημα ειναι δευτερου βαθμου, σωστα?
Αν ειναι μεγαλυτερου τι κανω? :-\
Αν ειναι μεγαλυτερου τι κανω? :-\
Γενικά σαν ts παίρνουμε το 4/σ, όπου σ η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 25, 2014, 20:53:01 pm
Οταν εχει προδιαγραφει για χρονο ανοδο (πχ ts<0.7) , μπορω να παω απο τον τυπο που λεει στο βιβλιο οτι ισχυει (προσεγγιστικα) σ>4.16/0.7 αν το συστημα ειναι δευτερου βαθμου, σωστα?
Αν ειναι μεγαλυτερου τι κανω? :-\
Αν ειναι μεγαλυτερου τι κανω? :-\
Γενικά σαν ts παίρνουμε το 4/σ, όπου σ η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος.
Ok. Αρα στο θεμα 2 του σεπτ που ζηταει αιτιολογηση για το που θα μπει το μηδενικο μπορω να πω οτι θα το βαλω κοντα στον κυριαρχο πολο. Μπορω ομως να βαλω μ = 5? Η πρεπει να πω οτι θα το βαλω κοντα στον κυριαρχο πολο? Και αν το βαλω κοντα στον κυριαρχο πολο τοτε τι θεωρω σαν ts?
Sorry παιδια για το μπαραζ ερωτησεων αλλα ειναι το σημειο που κολλαω αφανταστα! :(
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 25, 2014, 21:05:53 pm
Οταν εχει προδιαγραφει για χρονο ανοδο (πχ ts<0.7) , μπορω να παω απο τον τυπο που λεει στο βιβλιο οτι ισχυει (προσεγγιστικα) σ>4.16/0.7 αν το συστημα ειναι δευτερου βαθμου, σωστα?
Αν ειναι μεγαλυτερου τι κανω? :-\
Αν ειναι μεγαλυτερου τι κανω? :-\
Γενικά σαν ts παίρνουμε το 4/σ, όπου σ η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος.
Ok. Αρα στο θεμα 2 του σεπτ που ζηταει αιτιολογηση για το που θα μπει το μηδενικο μπορω να πω οτι θα το βαλω κοντα στον κυριαρχο πολο. Μπορω ομως να βαλω μ = 5? Η πρεπει να πω οτι θα το βαλω κοντα στον κυριαρχο πολο? Και αν το βαλω κοντα στον κυριαρχο πολο τοτε τι θεωρω σαν ts?
Sorry παιδια για το μπαραζ ερωτησεων αλλα ειναι το σημειο που κολλαω αφανταστα! :(
Μπορείς να πεις ότι θα το βάλεις στο 5, οπότε να απαλειφθεί με τον αντίστοιχο πόλο. Έπειτα, αν ο πόλος (από αυτού που θα μείνουν, μιας και θα έχεις διώξει αυτόν στο 5) με την μικρότερη απόλυτη τιμή πραγματικού μέρους σ ικανοποιεί τον περιορισμό για το χρόνο ανόδου που έχεις, είσαι οκ. ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 25, 2014, 21:07:23 pm
Οταν εχει προδιαγραφει για χρονο ανοδο (πχ ts<0.7) , μπορω να παω απο τον τυπο που λεει στο βιβλιο οτι ισχυει (προσεγγιστικα) σ>4.16/0.7 αν το συστημα ειναι δευτερου βαθμου, σωστα?
Αν ειναι μεγαλυτερου τι κανω? :-\
Αν ειναι μεγαλυτερου τι κανω? :-\
Γενικά σαν ts παίρνουμε το 4/σ, όπου σ η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος.
Ok. Αρα στο θεμα 2 του σεπτ που ζηταει αιτιολογηση για το που θα μπει το μηδενικο μπορω να πω οτι θα το βαλω κοντα στον κυριαρχο πολο. Μπορω ομως να βαλω μ = 5? Η πρεπει να πω οτι θα το βαλω κοντα στον κυριαρχο πολο? Και αν το βαλω κοντα στον κυριαρχο πολο τοτε τι θεωρω σαν ts?
Sorry παιδια για το μπαραζ ερωτησεων αλλα ειναι το σημειο που κολλαω αφανταστα! :(
Μπορείς να πεις ότι θα το βάλεις στο 5, οπότε να απαλειφθεί με τον αντίστοιχο πόλο. Έπειτα, αν ο πόλος (από αυτού που θα μείνουν, μιας και θα έχεις διώξει αυτόν στο 5) με την μικρότερη απόλυτη τιμή πραγματικού μέρους σ ικανοποιεί τον περιορισμό για το χρόνο ανόδου που έχεις, είσαι οκ. ;)
Οκ, ευχαριστω!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 25, 2014, 23:15:24 pm
Στο θεμα 2 του Σεπτεμβριου 2013 στο ερωτημα β ζηταει να υπολογιστει το ακριβες περιθωριο φασης.
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 26, 2014, 00:17:04 am
Στο θεμα 2 του Σεπτεμβριου 2013 στο ερωτημα β ζηταει να υπολογιστει το ακριβες περιθωριο φασης.
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Τον όρο 1/(s+20) δεν έχει κανένα λόγο να τον αγνοήσεις! Γενικά έναν πόλο, στο περιθώριο φάσης, θα ήταν αποδεκτό να τον αγνοήσεις αν ήταν πχ τουλάχιστον δεκαπλάσιος από τη συχνότητα ωc.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 26, 2014, 01:46:06 am
Στο θεμα 2 του Σεπτεμβριου 2013 στο ερωτημα β ζηταει να υπολογιστει το ακριβες περιθωριο φασης.
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Τον όρο 1/(s+20) δεν έχει κανένα λόγο να τον αγνοήσεις! Γενικά έναν πόλο, στο περιθώριο φάσης, θα ήταν αποδεκτό να τον αγνοήσεις αν ήταν πχ τουλάχιστον δεκαπλάσιος από τη συχνότητα ωc.
Thank you! Ξανα!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 26, 2014, 03:46:38 am
Στο θεμα 2 του Σεπτεμβριου 2013 στο ερωτημα β ζηταει να υπολογιστει το ακριβες περιθωριο φασης.
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Τον όρο 1/(s+20) δεν έχει κανένα λόγο να τον αγνοήσεις! Γενικά έναν πόλο, στο περιθώριο φάσης, θα ήταν αποδεκτό να τον αγνοήσεις αν ήταν πχ τουλάχιστον δεκαπλάσιος από τη συχνότητα ωc.
Αν θυμαμαι καλα για να βρω το ωc, και απο εκει το περιθωριο φασης, αν βρισκεται πριν το 20rad/sec (που μπορω να το ξερω απο το προσεγγιστικο Bode) τοτε μπορω να το αγνοησω, ετσι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 26, 2014, 04:04:35 am
Στο θεμα 2 του Σεπτεμβριου 2013 στο ερωτημα β ζηταει να υπολογιστει το ακριβες περιθωριο φασης.
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Επειδη ζηταει το ακριβες στο υπολογισμο του θα λαβω υποψη μου τον ορο 1/(s+20), σωστα? (Γιατι η διαφορα ειναι μεγαλουτσικη αν το παραλειψω.)
Τον όρο 1/(s+20) δεν έχει κανένα λόγο να τον αγνοήσεις! Γενικά έναν πόλο, στο περιθώριο φάσης, θα ήταν αποδεκτό να τον αγνοήσεις αν ήταν πχ τουλάχιστον δεκαπλάσιος από τη συχνότητα ωc.
Αν θυμαμαι καλα για να βρω το ωc, και απο εκει το περιθωριο φασης, αν βρισκεται πριν το 20rad/sec (που μπορω να το ξερω απο το προσεγγιστικο Bode) τοτε μπορω να το αγνοησω, ετσι?
Ναι, οποιονδήποτε πόλο είναι πριν το ωc μπορείς να τον αγνοήσεις (αρκεί να λάβεις υπόψη το DC κέρδος που αυτός προσφέρει) για την εύρεση του ωc.
Αυτό που είπα πριν, για να διευκρινίσω, είναι ότι δεν μπορείς να αγνοήσεις έναν πόλο για την εύρεση της φάσης της συνάρτησης μεταφοράς σου (για την εύρεση της ωc της συνάρτησης μεταφοράς σου, αντιθέτως, μπορείς εφόσον ισχύει ο περιορισμός που έγραψα παραπάνω).
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 26, 2014, 21:23:42 pm
Τελικα μπορει καποιος να απαντησει με σιγουρια τι παιζει με αυτο το θεμα με το περιθωριο κερδους??
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 26, 2014, 21:40:31 pm
Τελικα μπορει καποιος να απαντησει με σιγουρια τι παιζει με αυτο το θεμα με το περιθωριο κερδους??
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Όταν έχεις μια συνάρτηση ανοιχτού βρόχου A(s), για να βρεις το περιθώριο κέρδους, κάνεις τα εξής:
- Βάζεις ένα κέρδος Κ, οπότε η συνάρτηση ανοιχτού βρόχου σου είναι τώρα Κ * Α(s).
- Βρίσκεις τη συνάρτηση κλειστού βρόχου, έστω H(s).
- Κάνεις Routh για την H(s), και λες πως οι συντελεστές της πρώτης στήλης πρέπει να είναι θετικοί. Έτσι, βγάζεις έναν περιορισμό Κ < C.
- Αυτό το C είναι το περιθώριο κέρδους. Αν θες να το βρεις σε dB, είναι 20 * logC.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 26, 2014, 22:02:05 pm
αυτο που λες εσυ ειναι αυτο που ειπε και ο σταμουλης στην ταξη.κατι που λεει ενα ποστ σε προηγουμενη σελιδα που ειναι K/Ko και καλα,τι ειναι αυτο?το εχω δει και σε κατι λυμενα θεματα αυτο να το θετει ετσι.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 26, 2014, 22:38:01 pm
Τελικα μπορει καποιος να απαντησει με σιγουρια τι παιζει με αυτο το θεμα με το περιθωριο κερδους??
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Οταν ζητειται το περιθωριο κερδους σε μια συναρτηση ανοιχτου βροχου,σχηματιζουμε την συναρτηση κλειστου βροχου και κανουμε Routh στην χαρακτηριστικη εξισωση της ΣΜΚΒ.Μεχρι εδω πιστευω ειμαι οκ.
Μετα με τον περιορισμο για την ευσταθεια οι συντελεστες στον Routh πρεπει να ειναι θετικοι ωστε να υπαρχει ευσταθεια.Απο κει προκυπτει μια ανισωση ας πουμε. Μετα τι στο καλο κανω για να βρω το περιθωριο κερδους? Ειδα κατι και στις σημειωσεις του Σταμουλη και μπερδευτηκα ρε φιλε.
Ας πουμε βρικσω κ<5 απο το Routh.Αυτο το κ τι ειναι?
Ο Σταμουλης εχει λυσει μια ασκηση και λεει : Περιθωριο κερδους =20logk=20log5..
Ειναι σωστο αυτο,η εγινε λαθος στην αντιγραφη ας πουμε?Γιατι και ακαπου αλλου διαβασα οτι αυτο το κ ειναι ενας λογος με 2 κερδη μεσα...
Αν μπορει καποιος ας με βοηθησει.
Όταν έχεις μια συνάρτηση ανοιχτού βρόχου A(s), για να βρεις το περιθώριο κέρδους, κάνεις τα εξής:
- Βάζεις ένα κέρδος Κ, οπότε η συνάρτηση ανοιχτού βρόχου σου είναι τώρα Κ * Α(s).
- Βρίσκεις τη συνάρτηση κλειστού βρόχου, έστω H(s).
- Κάνεις Routh για την H(s), και λες πως οι συντελεστές της πρώτης στήλης πρέπει να είναι θετικοί. Έτσι, βγάζεις έναν περιορισμό Κ < C.
- Αυτό το C είναι το περιθώριο κέρδους. Αν θες να το βρεις σε dB, είναι 20 * logC.
K*gm = k0 =>
gm=C/K ;
σε 329 Πετρίδη
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 26, 2014, 22:53:20 pm
οκ.αρα το περιθωριο κερδους ειναι 20logKo?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 26, 2014, 23:00:16 pm
οκ.αρα το περιθωριο κερδους ειναι 20logKo?
σε dB ναιTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 26, 2014, 23:37:45 pm
αφου το περιθωριο κερδους ειναι gm=Kο/K γιατι σε db δεν ειναι 20log(K/Ko)? ρωταω απλα για να καταλαβω τι παιζει,δεν θελω να σε αμφισβητησω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 26, 2014, 23:58:30 pm
αφου το περιθωριο κερδους ειναι gm=Kο/K γιατι σε db δεν ειναι 20log(K/Ko)? ρωταω απλα για να καταλαβω τι παιζει,δεν θελω να σε αμφισβητησω.
όπα ναι 20log(gm) θα είναι εκ παραδρομής είπα ναι , λογο του log
exomag επιβεβαιώνεις;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 00:21:17 am
Εφόσον έχεις μια συνάρτηση ανοιχτού βρόχου A(s) που περιέχει ήδη ένα κέρδος Κ μέσα, τότε (σύμφωνα με τη μεθοδολογία που είπα πριν), για να βρεις το περιθώριο κέρδους θα βάλεις μπροστά ένα άλλο κέρδος (έστω G), οπότε η συνάρτηση ανοιχτού βρόχου σου τελικά θα είναι G * A(s) που έχει κέρδος G * K.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 00:26:18 am
Εφόσον έχεις μια συνάρτηση ανοιχτού βρόχου A(s) που περιέχει ήδη ένα κέρδος Κ μέσα, τότε (σύμφωνα με τη μεθοδολογία που είπα πριν), για να βρεις το περιθώριο κέρδους θα βάλεις μπροστά ένα άλλο κέρδος (έστω G), οπότε η συνάρτηση ανοιχτού βρόχου σου τελικά θα είναι G * A(s) που έχει κέρδος G * K.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
ναι έτσι συμφωνώ. Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 00:41:53 am
Εφόσον έχεις μια συνάρτηση ανοιχτού βρόχου A(s) που περιέχει ήδη ένα κέρδος Κ μέσα, τότε (σύμφωνα με τη μεθοδολογία που είπα πριν), για να βρεις το περιθώριο κέρδους θα βάλεις μπροστά ένα άλλο κέρδος (έστω G), οπότε η συνάρτηση ανοιχτού βρόχου σου τελικά θα είναι G * A(s) που έχει κέρδος G * K.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
οκ παω πασο.συμφωνω κεγω μαυτο.αν δεν ξερεις το K τι σκατα κανεις?απλα το αφηνεις συναρτησει του Κ ας πουμε?γιατι ας πουμε τον σεπτεμβριο του 13 δεν εδινε το Κ στο πρωτο θεμα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 01:00:35 am
Εφόσον έχεις μια συνάρτηση ανοιχτού βρόχου A(s) που περιέχει ήδη ένα κέρδος Κ μέσα, τότε (σύμφωνα με τη μεθοδολογία που είπα πριν), για να βρεις το περιθώριο κέρδους θα βάλεις μπροστά ένα άλλο κέρδος (έστω G), οπότε η συνάρτηση ανοιχτού βρόχου σου τελικά θα είναι G * A(s) που έχει κέρδος G * K.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
Μέσω Routh, θα βρεις ένα περιορισμό για το κέρδος G * K, έστω C (δηλαδή G * K < C). Το περιθώριο κέρδους σου θα είναι το 20 * logG.
οκ παω πασο.συμφωνω κεγω μαυτο.αν δεν ξερεις το K τι σκατα κανεις?απλα το αφηνεις συναρτησει του Κ ας πουμε?γιατι ας πουμε τον σεπτεμβριο του 13 δεν εδινε το Κ στο πρωτο θεμα.
Έτσι όπως είναι διατυπωμένο το θέμα, είναι λίγο περίεργο. Λογικά θα βρεις τη μέγιστη τιμή του G * K (έστω C), και θα πεις ότι το περιθώριο κέρδους είναι 20 * log(C/K).
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 01:05:20 am
ναι αλλα το Κ δεν το ξερεις...γιαυτο ρωταω τοση ωρα. :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 01:08:38 am
ναι αλλα το Κ δεν το ξερεις...γιαυτο ρωταω τοση ωρα. :P
Nαι κι εγω ειχα θεμα μ'αυτο. Αν απλα δωσεις σαν απαντηση το μεγιστο Κ το οποιο βρηκαμε απο το Routh δεν θα ειναι δεκτο??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 01:11:36 am
Και στο θεμα δυο του Σεπτεμβριου 2012 παλι θα διναμε απαντηση σε db συναρτηση του Κ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 01:43:41 am
Χμ, σε αυτήν την περίπτωση μπορεί να θέλει να πεις το μέγιστο Κ για το οποίο παραμένει ευσταθής η ΣΜΚΒ. Δηλαδή να κάνεις Routh, και να βρεις τον περιορισμό για το Κ, και να πεις ότι αυτή η τιμή είναι το περιθώριο κέρδους.
Είναι λίγο αμφιλεγόμενο το θέμα :-\
Είναι λίγο αμφιλεγόμενο το θέμα :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 01:52:12 am
κατι μου ειπαν οτι τους ειπε τον Σεπτεμβρη να το αφησουν συναρτησει του Κ αλλα δεν ξερω τελικα ποια ειναι η απαντησις.
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 02:01:47 am
κατι μου ειπαν οτι τους ειπε τον Σεπτεμβρη να το αφησουν συναρτησει του Κ αλλα δεν ξερω τελικα ποια ειναι η απαντησις.
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
Πιστευω αν το δωσεις συναρτησει του Κ και το δικαιολογησεις θα εισαι οκ. Για σιγουρια λεω να γραψουμε και τα δυο!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 02:46:42 am
κατι μου ειπαν οτι τους ειπε τον Σεπτεμβρη να το αφησουν συναρτησει του Κ αλλα δεν ξερω τελικα ποια ειναι η απαντησις.
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
.Δηλαδη εχεις ας πουμε Gm=Ko/K οπου το Κο το υπολογιζεις απο Routh,που ειναι το μεγιστο Κ για να εισαι στα ορια της ευσταθειας,αλλα αν εξαρχης δεν σου δινει ενα Κ στην συναρτηση ανοιχτου βροχου ,δεν μπορεις να υπολογισεις νουμερο.
Οποτε το ρωταμε και εκεινη την ωρα και βλεπουμε?Γιατι για να απαντησει σε μαιλ λιγο δυσκολο το κοβω. ;D
Πιστευω αν το δωσεις συναρτησει του Κ και το δικαιολογησεις θα εισαι οκ. Για σιγουρια λεω να γραψουμε και τα δυο!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 13:49:41 pm
Όταν λέει ts<... , ισχύει ts=4.16/σ, όπου το σ βρίσκεται από τον παρανομαστή της συνάρτησης κλειστού βρόχου.
Σωστό είναι αυτό;
- Αν είναι πρώτου βαθμού το σ είναι ίσο με τον πόλο
- Αν είναι δευτέρου βαθμού, είναι ίσο με το συντελεστή του s ,/2
- Αν είναι τρίτου βαθμού, είναι ίσο με το συντελεστή του s2 ,/2
Σωστό είναι αυτό;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 13:51:14 pm
Όταν λέει ts<... , ισχύει ts=4.16/σ, όπου το σ βρίσκεται από τον παρανομαστή της συνάρτησης κλειστού βρόχου.
Σωστό είναι αυτό;
- Αν είναι πρώτου βαθμού το σ είναι ίσο με τον πόλο
- Αν είναι δευτέρου βαθμού, είναι ίσο με το συντελεστή του s ,/2
- Αν είναι τρίτου βαθμού, είναι ίσο με το συντελεστή του s2 ,/2
Σωστό είναι αυτό;
Γενικά σαν ts παίρνουμε το 4/σ, όπου σ η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος.
Για την περίπτωση πρώτου βαθμού είναι σωστό αυτό που γράφεις. Για τις άλλες δύο δεν είναι αναγκαστικό να ισούται το σ με αυτό που γράφεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 13:57:23 pm
Για την περίπτωση πρώτου βαθμού είναι σωστό αυτό που γράφεις. Για τις άλλες δύο δεν είναι αναγκαστικό να ισούται το σ με αυτό που γράφεις.
Σε αυτό που λες αν έχω ολοκληρωτή στον παρανομαστή τύπου 1 τότε ο χρόνος είναι άπειρος;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 13:58:46 pm
για τη δεύτερη είναι αφου είναι το ζωn, γενικά είναι ένα παλιό ποστ για αυτό ρωτάω
Σε τρίτου βαθμού πώς τον βρίσκουμε;
Σε τρίτου βαθμού πώς τον βρίσκουμε;
Για την περίπτωση πρώτου βαθμού είναι σωστό αυτό που γράφεις. Για τις άλλες δύο δεν είναι αναγκαστικό να ισούται το σ με αυτό που γράφεις.
Σε αυτό που λες αν έχω ολοκληρωτή στον παρανομαστή τύπου 1 τότε ο χρόνος είναι άπειρος;
Δεν ισχύει αναγκαστικά για τη δευτέρου βαθμού. Αυτό που γράφεις είναι υποπερίπτωση, μόνο με την προϋπόθεση ότι ο συντελεστής του όρου s2 είναι μονάδα.
Μη το σκέφτεσαι με έτοιμους τύπος. Το σ είναι η μικρότερη από τις απόλυτες τιμές του πραγματικού μέρους των πόλων ενός συστήματος (ευσταθούς). Οπότε απλά θα πρέπει να βρεις τις ρίζες του πολυωνύμου του παρανομαστή.
Αν είναι τρίτου βαθμού ή θα χρησιμοποιήσεις κομπιουτεράκι ή θα πρέπει να αγνοήσεις κάποιον πόλο.
Αν έχεις σ = 0, τότε νομίζω πως όντως ο χρόνος ts θα είναι άπειρος.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 14:03:58 pm
Τότε και σόρρυ αν πω βλακεία.
Στο θέμα 2 Ιανουάριος 2011
δίνεται ένα σύστημα της μορφής (s+2)/(s+3)(s+6).
Και ζητείται να σχεδιάσουμε ένα σύστημα με 4 προδιαγραφές δύο εκ των οποίων είναι:
essv<0.5
ts<1s
Άρα θα χρειαστούμε ολοκληρωτή άρα θα έχουμε άπειρο ts;
Στο θέμα 2 Ιανουάριος 2011
δίνεται ένα σύστημα της μορφής (s+2)/(s+3)(s+6).
Και ζητείται να σχεδιάσουμε ένα σύστημα με 4 προδιαγραφές δύο εκ των οποίων είναι:
essv<0.5
ts<1s
Άρα θα χρειαστούμε ολοκληρωτή άρα θα έχουμε άπειρο ts;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 14:07:12 pm
Τότε και σόρρυ αν πω βλακεία.
Στο θέμα 2 Ιανουάριος 2011
δίνεται ένα σύστημα της μορφής (s+2)/(s+3)(s+6).
Και ζητείται να σχεδιάσουμε ένα σύστημα με 4 προδιαγραφές δύο εκ των οποίων είναι:
essv<0.5
ts<1s
Άρα θα χρειαστούμε ολοκληρωτή άρα θα έχουμε άπειρο ts;
Στο θέμα 2 Ιανουάριος 2011
δίνεται ένα σύστημα της μορφής (s+2)/(s+3)(s+6).
Και ζητείται να σχεδιάσουμε ένα σύστημα με 4 προδιαγραφές δύο εκ των οποίων είναι:
essv<0.5
ts<1s
Άρα θα χρειαστούμε ολοκληρωτή άρα θα έχουμε άπειρο ts;
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 14:11:35 pm
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 14:15:30 pm
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Βάζεις, πχ, έναν ελεγκτή K/s. Μέσω του περιορισμού για το σφάλμα ταχύτητας που σου δίνεται, βρίσκεις έναν περιορισμό για το Κ. Έπειτα σχεδιάζεις τον ΓΤΡ του ΣΚΒ, και βλέπεις που βρίσκεται το σ για τις διάφορες τιμές του Κ (σ είναι η απόσταση από τον φανταστικό άξονα, του κοντινότερου σε αυτόν πόλο). Εφόσον για κάποια τιμή του Κ έχεις ένα δεκτό σ (που θα σου δώσει έναν δεκτό χρόνο αποκατάστασης δηλαδή), είσαι οκ. Αλλιώς, μπορείς να χρειαστεί να βάλεις ελεγκτή K(s+C)/s. (και να επαναλάβεις την ίδια διαδικασία)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 14:18:28 pm
οκ ευχαριστώ!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 14:19:06 pm
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Βάζεις, πχ, έναν ελεγκτή K/s. Μέσω του περιορισμού για το σφάλμα ταχύτητας που σου δίνεται, βρίσκεις έναν περιορισμό για το Κ. Έπειτα σχεδιάζεις τον ΓΤΡ του ΣΚΒ, και βλέπεις που βρίσκεται το σ για τις διάφορες τιμές του Κ (σ είναι η απόσταση από τον φανταστικό άξονα, του κοντινότερου σε αυτόν πόλο). Εφόσον για κάποια τιμή του Κ έχεις ένα δεκτό σ (που θα σου δώσει έναν δεκτό χρόνο αποκατάστασης δηλαδή), είσαι οκ. Αλλιώς, μπορείς να χρειαστεί να βάλεις ελεγκτή K(s+C)/s. (και να επαναλάβεις την ίδια διαδικασία)
ΓΤΡ θα κανεις με την συναρτηση ανοικτου βροχου, ετσι δεν ειναι? Ειχα κι εγω ενα θεμα με αυτη την ερωτηση γιατι δεν μπορω απο τον ΓΤΡ της συναρητησης μεταφορας ανοικτου βροχου να βαλω καπως το μηδενικο για να ειναι ο χρονος αποκαταστασης αυτος που ζηταει! :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 27, 2014, 14:23:50 pm
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Βάζεις, πχ, έναν ελεγκτή K/s. Μέσω του περιορισμού για το σφάλμα ταχύτητας που σου δίνεται, βρίσκεις έναν περιορισμό για το Κ. Έπειτα σχεδιάζεις τον ΓΤΡ του ΣΚΒ, και βλέπεις που βρίσκεται το σ για τις διάφορες τιμές του Κ (σ είναι η απόσταση από τον φανταστικό άξονα, του κοντινότερου σε αυτόν πόλο). Εφόσον για κάποια τιμή του Κ έχεις ένα δεκτό σ (που θα σου δώσει έναν δεκτό χρόνο αποκατάστασης δηλαδή), είσαι οκ. Αλλιώς, μπορείς να χρειαστεί να βάλεις ελεγκτή K(s+C)/s. (και να επαναλάβεις την ίδια διαδικασία)
ΓΤΡ θα κανεις με την συναρτηση ανοικτου βροχου, ετσι δεν ειναι? Ειχα κι εγω ενα θεμα με αυτη την ερωτηση γιατι δεν μπορω απο τον ΓΤΡ της συναρητησης μεταφορας ανοικτου βροχου να βαλω καπως το μηδενικο για να ειναι ο χρονος αποκαταστασης αυτος που ζηταει! :-\
Ο παρανομαστής της ΣΜΚΒ είναι η Χαρακτηριστική Εξίσωση (ΧΕ). ΓΤΡ κάνεις στην εξίσωση ΧΕ = 0, που πρέπει να φέρεις στη μορφή Κ * H(s) = -1. Για αυτήν την Η(s) θα κάνεις τη σχεδίαση.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 14:27:36 pm
Άμα βάλεις ελεγκτή με κέρδος και ολοκληρωτή, τότε καθώς αυξάνεται το κέρδος ο πόλος της ΣΜΚΒ θα απομακρύνεται από το κέντρο των αξόνων. Οπότε δεν θα έχεις άπειρο ts, εφόσον βάλεις και κάποιο κέρδος στον ελεγκτή σου ;)
Βάζεις, πχ, έναν ελεγκτή K/s. Μέσω του περιορισμού για το σφάλμα ταχύτητας που σου δίνεται, βρίσκεις έναν περιορισμό για το Κ. Έπειτα σχεδιάζεις τον ΓΤΡ του ΣΚΒ, και βλέπεις που βρίσκεται το σ για τις διάφορες τιμές του Κ (σ είναι η απόσταση από τον φανταστικό άξονα, του κοντινότερου σε αυτόν πόλο). Εφόσον για κάποια τιμή του Κ έχεις ένα δεκτό σ (που θα σου δώσει έναν δεκτό χρόνο αποκατάστασης δηλαδή), είσαι οκ. Αλλιώς, μπορείς να χρειαστεί να βάλεις ελεγκτή K(s+C)/s. (και να επαναλάβεις την ίδια διαδικασία)
ΓΤΡ θα κανεις με την συναρτηση ανοικτου βροχου, ετσι δεν ειναι? Ειχα κι εγω ενα θεμα με αυτη την ερωτηση γιατι δεν μπορω απο τον ΓΤΡ της συναρητησης μεταφορας ανοικτου βροχου να βαλω καπως το μηδενικο για να ειναι ο χρονος αποκαταστασης αυτος που ζηταει! :-\
Ο παρανομαστής της ΣΜΚΒ είναι η Χαρακτηριστική Εξίσωση (ΧΕ). ΓΤΡ κάνεις στην εξίσωση ΧΕ = 0, που πρέπει να φέρεις στη μορφή Κ * H(s) = -1. Για αυτήν την Η(s) θα κάνεις τη σχεδίαση.
Σορρυ Exomag, χαζη ερωτηση!! Εφαγα κολλημα!!
Για τα Θεματα του Ιανουαριου Batman βρηκα το εξης topic:https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488 (https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488)
Με τρομαξε λιγο ειναι η αληθεια! :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:05:32 pm
Περίεργα πράγματα συμβαίνουν.
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:13:07 pm
θέμα 2 Ιανουάριος 13
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ/(s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ/(s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:17:53 pm
θέμα 2 Ιανουάριος 13
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ/(s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Και εγώ έτσι το σκέφτηκα.λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ/(s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 15:19:23 pm
θέμα 2 Ιανουάριος 13
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Συνεχιζεις λιγο ακομα και βρισκεις οτι με την K / (s+6) δεν μπορεις να εχεις απειρο περιθωριο κερδους, που ειναι η επομενη προδιαγραφη, (σχειδιασε ΓΤΡ για να το δειξεις).
Αρα διαλεγεις τον αλλο ελεγκτη και πας απο την αρχη.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:20:37 pm
Περίεργα πράγματα συμβαίνουν.
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
αν στις χαμηλές συχνότητες έχεις μόνο αναλογικό κέρδος
20log|Α(0.1i)|-20log(|A(wbi|)=3db (αμα έχεις διάγραμμα υποθέτω μπορείς να πετάξεις τους διαφόρους όρους οι οποίοι επηρεάζουν την απόκριση μετα το wb , αλλιως άντε να το λύσεις)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:22:04 pm
θέμα 2 Ιανουάριος 13
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Συνεχιζεις λιγο ακομα και βρισκεις οτι με την K / (s+6) δεν μπορεις να εχεις απειρο περιθωριο κερδους, που ειναι η επομενη προδιαγραφη, (σχειδιασε ΓΤΡ για να το δειξεις).
Αρα διαλεγεις τον αλλο ελεγκτη και πας απο την αρχη.
Διπλή δουλέια αμα έιναι να κάνω ΓΤΡ δύο φόρες. Γενικά το Κ σε τι εύρος τιμών είναι αποδεκτό;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 15:22:22 pm
Περίεργα πράγματα συμβαίνουν.
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
Άλλη απορία όταν ψάχνω εύρος ζώνης σε σύστημα κλειστού βρόχου
βρίσκω τη συχνότητα για την οποία ισχύει ότι : πλάτος = DCκέδορς -3db;
Σου ζηταει καποιο περιορισμο για το ευρος ζωνης η σου ζηταει να το υπολογισεις?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 15:23:45 pm
θέμα 2 Ιανουάριος 13
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
λέει να εξετασθεί ποίος απο τους 2 ελεγκτές πρέπει να χρησιμοποιηθεί
και έχει κ/(s+6) vs k(s+μ)/(s+6)
η παρακάτω λογική (για να μην υπολογίσουμε τα πάντα και γρήγορα να διαλέξουμε έναν απο τους 2 ) είναι αποδεκτή;
έστω ότι έιναι ο Κ / (s+6) και υπολογίζω το β ερώτημα (περιορισμό ess) και βγαίνει οτι κ=~1296 πολύ πολύ μεγάλο αρα παίρνω τον άλλο ελεκτή και υπολογίζω τις τιμές κ,μ
Συνεχιζεις λιγο ακομα και βρισκεις οτι με την K / (s+6) δεν μπορεις να εχεις απειρο περιθωριο κερδους, που ειναι η επομενη προδιαγραφη, (σχειδιασε ΓΤΡ για να το δειξεις).
Αρα διαλεγεις τον αλλο ελεγκτη και πας απο την αρχη.
Διπλή δουλέια αμα έιναι να κάνω ΓΤΡ δύο φόρες. Γενικά το Κ σε τι εύρος τιμών είναι αποδεκτό;
Γενικα το ΓΤΡ για την πρωτη βγαινει αρκετα ευκολα, σε δυο σειρες. Μπορεις να ξεκινησεις απο τον περιορισμο για το περιθωριο κερδους να δειξεις οτι δεν γινεται και να συνεχισεις με την δευτερη. Δεν νομιζω να μας εδωσε (Ο σταμουλης τουλαχιστον) καποιον περιορισμο για το Κ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:24:09 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
Είναι το 1 θέμα σεπτέμβρης 2012
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 15:27:33 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
Είναι το 1 θέμα σεπτέμβρης 2012
Χμμμ, εγω κολλησα λιγο σ'αυτην για το πως θα βρω το ω2. Οταν την συνεχισω και βγαλω κανενα αποτελεσμα θα σ πω. Για την ωρα σορρυ. :(
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:28:44 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
Είναι το 1 θέμα σεπτέμβρης 2012
Χμμμ, εγω κολλησα λιγο σ'αυτην για το πως θα βρω το ω2. Οταν την συνεχισω και βγαλω κανενα αποτελεσμα θα σ πω. Για την ωρα σορρυ. :(
και υπολογίζεται απο εκεί και βγαίνει κάπου στα 200 κοντά.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:30:13 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:31:00 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Ποια κρατάω;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:38:13 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Ποια κρατάω;
κατσε να το λύσω και εγώ να στο επιβεβαιώσω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 27, 2014, 15:39:53 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Ποια κρατάω;
κατσε να το λύσω και εγώ να στο επιβεβαιώσω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 15:47:43 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Ποια κρατάω;
κατσε να το λύσω και εγώ να στο επιβεβαιώσω
Το εύρος ζώνης ενός συστήματος ωb αντιστοιχέι στην συχνότητα για την οποία το μέτρο της απόκρισης συχνότητας εξασθενεί κατα 3dB σε σχέσξ με την τιμή που έχει στην περιοχή χαμηλών συχνότήτων.
Δες τώρα το διάγραμμα. Στις χαμηλές συχνότητες έχει 20dB. Λιγότερο απο 20dB έχεις μετα το ω2
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 15:48:06 pm
Να το υπολογίσω.
Είναι το 1 θέμα σεπτέμβρης 2012
ψάχνεις wb τέτοιο ωστε |Α(j wb)|=17dbΕίναι το 1 θέμα σεπτέμβρης 2012
Ποια κρατάω;
κατσε να το λύσω και εγώ να στο επιβεβαιώσω
Γιατη στην ωb εχεις πτωση 3dB απο το κερδος που εχεις στις χαμηλες συχνοτητες,
πριν την ω2 το διαγραμμα δεν ειναι πουθενα κατω απο 20dΒ που ειναι το κερδος στις χαμηλες συχνοτητες
αρα η ωb θα ειναι μετα την ω2.
Με προλαβες! :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 16:31:12 pm
αν δεν έχω κάνει λάθος
10(s+1)
Η(s) = ----------------------------
(s/5 +1)(s/20 +1)
wb=139.7rad/s (Ti 89)
10(s+1)
Η(s) = ----------------------------
(s/5 +1)(s/20 +1)
wb=139.7rad/s (Ti 89)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 16:43:10 pm
αν δεν έχω κάνει λάθος
10(s+1)
Η(s) = ----------------------------
(s/5 +1)(s/20 +1)
wb=139.7rad/s (Ti 89)
10(s+1)
Η(s) = ----------------------------
(s/5 +1)(s/20 +1)
wb=139.7rad/s (Ti 89)
Θαυματα κανει αυτο το Τi! ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 17:04:09 pm
Οταν στον ΓΤΡ εχω δυο ασυμπτωτες με γωνιες +- 90 και θελω το κεντρο τους να ειναι πιο αριστερα απο εναν αριθμο στο ΑΗΠ, εστω απο το 3, γραφω κεντρο < -3 και εφαρμοζω τον τυπο??
Και κατι ακομα, στο θεμα 2 ΙΑΝ-2013 για το ερωτημα δ, ειναι λαθος να θεωρησω απο τις προηγουμενες προδιαγραφες τιμες για τα k και μ και να ελεγχω αν ισχυει και η τελευταια? Και σε περιπτωση που δεν ισχυει να δωσω αλλη τιμη στο k.
Και κατι ακομα, στο θεμα 2 ΙΑΝ-2013 για το ερωτημα δ, ειναι λαθος να θεωρησω απο τις προηγουμενες προδιαγραφες τιμες για τα k και μ και να ελεγχω αν ισχυει και η τελευταια? Και σε περιπτωση που δεν ισχυει να δωσω αλλη τιμη στο k.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 19:57:02 pm
εχει κανει κανεις τον αυγουστο του 10? μπορει κανεις να μ πει στο περιπου πως βγαινει o ΓΤΡ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pentium4 on January 27, 2014, 20:27:26 pm
εχει κανει κανεις τον αυγουστο του 10? μπορει κανεις να μ πει στο περιπου πως βγαινει o ΓΤΡ?
δες αυτα μήπως βοηθήσουν
ps : ευχαριστούμε τον πολυαγαπημένο μας Marmotako 8))
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 20:30:07 pm
εχει κανει κανεις τον αυγουστο του 10? μπορει κανεις να μ πει στο περιπου πως βγαινει o ΓΤΡ?
θα το πίασω αργότερα
στον Σεπτ το 13
ο ΓΤΡ ειναι οπως στην εικονα;
πολοι -5,-7,-18
κεντρο ασύμπτωτων -10
(http://i42.tinypic.com/2mdotom.jpg)
αυτό που δεν μου κόλαγε είναι η γωνία αναχώρησης απο τον -7 κανονικά ειναι 180μοιρες αλλα πως θα παέι με τέτοια γωνία στο σημέιο θλάσης που έιναι νωρίτερα;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 20:34:34 pm
Κεγω ετσι βρηκα τον Σεπτεμβριο του 13,πριν προστεθει το μηδενικο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 21:11:30 pm
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 22:28:47 pm
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 22:29:40 pm
Κεγω ετσι βρηκα τον Σεπτεμβριο του 13,πριν προστεθει το μηδενικο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
Κι εγω ετσι το βρηκα. ( και το Matlab )
Στο επομενο ερωτημα για το ελαχιστο α τι εβγαλες?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 22:31:33 pm
Κεγω ετσι βρηκα τον Σεπτεμβριο του 13,πριν προστεθει το μηδενικο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
αυγουστος του 10 ΓΤΡ.για δειτε το λιγο.
Κι εγω ετσι το βρηκα. ( και το Matlab )
Στο επομενο ερωτημα για το ελαχιστο α τι εβγαλες?
για πες λιγο εσυ τι εβγαλες.δεν το εκανα ακομα.χαχα.αλλα τι κανεις ας πουμε?Routh και τετοια?Και για τον ΓΤΡ βρηκες και σημεια αποσχθσης ρε φιλε?ειναι 5ου βαθμου η συναρτηση να πουμε.Βρηκες και γωνιες αναχωρησης?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 22:38:24 pm
Σημεια αποσχισης δεν βρηκα εγω, γενικα για κανενα σχεδον δε βρισκω αν ειναι μεγαλου βαθμου. Μονο την εξισωση θα τους γραψω γιατι το κομπιουτερακι μου κλαταρει!
Το αλλο για να το λυσω επειδη δυο πολοι θα τεινουν ασυμπτωτικα στο απειρο με γωνιες +90 και -90 παιρνω περιορισμο οτι το κεντρο των ασυμπτωτων να ειναι στον αρνητικο ημιαξονα.
Αλλα μου βγαινει μια συνθηκη οτι πρεπει το α να ειναι μεγαλυτερο απο εναν αρνητικο αριθμο. Δεν μ αρεσε πολυ ομως γιατι στην εκφωνηση λεει οτι α>0.
Το αλλο για να το λυσω επειδη δυο πολοι θα τεινουν ασυμπτωτικα στο απειρο με γωνιες +90 και -90 παιρνω περιορισμο οτι το κεντρο των ασυμπτωτων να ειναι στον αρνητικο ημιαξονα.
Αλλα μου βγαινει μια συνθηκη οτι πρεπει το α να ειναι μεγαλυτερο απο εναν αρνητικο αριθμο. Δεν μ αρεσε πολυ ομως γιατι στην εκφωνηση λεει οτι α>0.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 22:41:57 pm
αυτο λογικα καπως με routh θα πρεπει να λυνεται ρε συ,γιατι λεει και για περιθωριο κερδους απειρο.Οποτε πρεπει απο Routh να βαλεις εκει περα να ειναι ολοι οι συντελεστες θετικοι και να βγαλεις καποιους περιορισμους.Αλλα εγω κολλαω στο K το οποιο δεν το ξερουμε,οποτε στον Routh θα εχεις 2 αγνωστους.Εκει τωρα δεν ξερω τι παιζει.Εσυ τι λες?
παντως παιζει να ειναι και αυτο που λες εσυ μονο με το ΟΑ αλλα μονο και μονο επειδη οι ασυμπτωτες των κλαδων ειναι -90 και 90 και ετσι δεν υπαρχει περιπτωση να τεμνει τον αξονα τον φανταστικο ,οταν το OA ειναι αρνητικο.Εσεις τι λετε ρε παιδια γιαυτο??
παντως παιζει να ειναι και αυτο που λες εσυ μονο με το ΟΑ αλλα μονο και μονο επειδη οι ασυμπτωτες των κλαδων ειναι -90 και 90 και ετσι δεν υπαρχει περιπτωση να τεμνει τον αξονα τον φανταστικο ,οταν το OA ειναι αρνητικο.Εσεις τι λετε ρε παιδια γιαυτο??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 22:48:57 pm
Κοιτα εγω με Routh δεν το σκεφτηκα καθολου, πηρα περιορισμο οτι αν το κεντρο των ασυμπτωτων ειναι στον αρνητικο ημιαξονα, τοτε αφου τεινουν με γωνιες +90 ο ενας πολος και -90 ο αλλος, δεν θα περνανε ποτε στο δεξι ημιεπιπεδο και αρα δεν θα περναει το συστημα σε ασταθεια για κανενα Κ. Αρα εχει απειρο περιθωριο κερδους. Δεν ειμαι και σιγουρος γιατι δεν ειδα να ακολουθει τετοιο συλλογισμο σε καμια λυμενη! Θα το δω αργοτερα αν ειναι και με Routh. Εσενα με ΓΤΡ και τετοιο συλλογισμο πως σου φαινεται? :-\
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 22:55:24 pm
Ναι συμφωνω απολυτα σε αυτα που λες. Το προσθεσα και στο σχολιο μου πανω και νμζω οτι μ φαινεται σωστο. Τωρα για το Routh ,δεν μπορεις να το κανεις αν δεν ξερεις την τιμη του Κ .Σε ενα λυμενο του Σταμουλη ,κανει Routh αλλα ειχε δωσει την τιμη του Κ ,οποτε στο Routh απλα επαιρνες εκει περα την ΧΕ του κλειστου βροχου και αν εκανες Routh μπορουσες να βγαλεις περιορισμο για το α.Αλλα τωρα που δεν σου δινεται το Κ δεν νμζω να γινεται με Routh,γιατι πρωτον βγαινει τεραστια η παρασταση και δευτερον εχεις 2 αγνωστους.
Μπορει κανεις αλλος να επιβεβαιωσει?
Μπορει κανεις αλλος να επιβεβαιωσει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 23:07:09 pm
απλα θες το κέντρο των ασύμπωτων να είναι στο Αριστερο ημιεπίπεδο έτσι ώστε οι κλάδοι να μην τέμνουν τον άξονα Ιm
Αφου δεν τέμνουν ποτε τον αξονα im (αφου οι ασύμπτωτες έιναι κάθετες) έχεις και άπειρο περιθώριο κέρδους.
ΟΑ=(-2α -1 )/2 <0 => a>-1/2
τώρα αυτό με το α>0 είναι λίγο περίεργο μπορούμε να πουμε οτι το 1 είναι μια τέτοια τιμή
αν κάνεις ρουθ απλα θέλεις να βγάλεις μια τιμή για το Κ που να ισχύει πάντα πχ Κ>(αρνητική συνθήκη) ( να ειναι ευσταθής για κάθε Κ)
αλλα είναι 4 βαθμού και θα έιναι μπελάς με 2 αγνώστους
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 27, 2014, 23:10:41 pm
απλα θες το κέντρο των ασύμπωτων να είναι στο Αριστερο ημιεπίπεδο έτσι ώστε οι κλάδοι να μην τέμνουν τον άξονα Ιm
Αφου δεν τέμνουν ποτε τον αξονα im (αφου οι ασύμπτωτες έιναι κάθετες) έχεις και άπειρο περιθώριο κέρδους.
ΟΑ=(-2α -1 )/2 <0 => a>-1/2
τώρα αυτό με το α>0 είναι λίγο περίεργο μπορούμε να πουμε οτι το 1 είναι μια τέτοια τιμή
αν κάνεις ρουθ απλα θέλεις να βγάλεις μια τιμή για το Κ που να ισχύει πάντα πχ Κ>(αρνητική συνθήκη) ( να ειναι ευσταθής για κάθε Κ)
αλλα είναι 4 βαθμού και θα έιναι μπελάς με 2 αγνώστους
συγγνωμη το (-2α-1)/2 πως προεκυψε???πως τους εγραψες τους πολους και τα μηδενικα??επισης συμφωνω αυτο με το α>0 ,απλα θεωρεις κατι πανω απο το 0 με βαση αυτα που λες.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 27, 2014, 23:17:46 pm
Στο τριτο θεμα την προδιαγραφη για το περιθωριο φασης πως την ικανοποιουμε?? Πρεπει να βρω το ωc ? Απο τον τυπο |Α(jωc)| = 1 προκυπτει ενα μακριναρι πραξεις!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 23:32:44 pm
απλα θες το κέντρο των ασύμπωτων να είναι στο Αριστερο ημιεπίπεδο έτσι ώστε οι κλάδοι να μην τέμνουν τον άξονα Ιm
Αφου δεν τέμνουν ποτε τον αξονα im (αφου οι ασύμπτωτες έιναι κάθετες) έχεις και άπειρο περιθώριο κέρδους.
ΟΑ=(-2α -1 )/2 <0 => a>-1/2
τώρα αυτό με το α>0 είναι λίγο περίεργο μπορούμε να πουμε οτι το 1 είναι μια τέτοια τιμή
αν κάνεις ρουθ απλα θέλεις να βγάλεις μια τιμή για το Κ που να ισχύει πάντα πχ Κ>(αρνητική συνθήκη) ( να ειναι ευσταθής για κάθε Κ)
αλλα είναι 4 βαθμού και θα έιναι μπελάς με 2 αγνώστους
συγγνωμη το (-2α-1)/2 πως προεκυψε???πως τους εγραψες τους πολους και τα μηδενικα??επισης συμφωνω αυτο με το α>0 ,απλα θεωρεις κατι πανω απο το 0 με βαση αυτα που λες.
(s+3)(s+4)
----------------------------------------------
(s-(-a-2i))(s-(-a+2i))(s-(-4+2i))(s-(-4-2i))
ao=(-a-2i -a+2i -4 +2i -4 -2i -(-)3 -(-)4) /(4-2)
ao=(-a -a -4 -4 +3 +4) /(4-2)
ao=(-2a -1 ) /(4-2)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 27, 2014, 23:35:03 pm
Στο τριτο θεμα την προδιαγραφη για το περιθωριο φασης πως την ικανοποιουμε?? Πρεπει να βρω το ωc ? Απο τον τυπο |Α(jωc)| = 1 προκυπτει ενα μακριναρι πραξεις!!
είχα απο πριν Κ>18είπα έστω Κ=20
βρίσκω το ωc
Βρίσκω Φm με Κ=20 και ωc και καλύπτει τον περιορισμό
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 00:20:53 am
Α, εθεσες τιμη για το Κ. Οποτε βγαινει ευκολα! Καλη φαση, δεν το σκεφτηκα! :D
Thank you!
Thank you!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 28, 2014, 00:55:46 am
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 28, 2014, 01:02:13 am
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mardi on January 28, 2014, 08:12:22 am
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 28, 2014, 15:33:34 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 28, 2014, 16:39:50 pm
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
ρε συ επηρεαζει το χρονο αποκαταστασης αφου αναλογα με το τι κερδος θα εχεις στον αριθμητη αλλαζει και η τιμη του ωn αρα και του χρονο αποκαταστασης.
διαφωνω δλδ με τον τροπο που υπολογιζεις τον χρονο αποκαταστασης,δες σελιδα 388 και σχεση 9.2.17
Νομιζω οτι αυτον τον τυπο π τον χρησιμοποιουμε πλεον παντου και εχει γινει σουπα για το Ts δλδ ts=4,16/a περισσοτερο ισχυει για ενα συστημα που εχει πολλους πολους. Εκτος εαν το σκεφτεσαι εσυ τωρα ετσι,γιατι υπολογισες το ζ και ειδες οτι ειναι μικροτερο απο 0,95 αρα και χρησιμοποιεις τον τυπο απο την σελις 388.Εγω νμζω γενικα οτι για ενα παρονομαστη του στυλ s^2+2ζωn+ωn^2 o χρονος αποκαταστασης ειναι ts=4,16/ζωn.Tι λετε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 18:27:50 pm
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
ρε συ επηρεαζει το χρονο αποκαταστασης αφου αναλογα με το τι κερδος θα εχεις στον αριθμητη αλλαζει και η τιμη του ωn αρα και του χρονο αποκαταστασης.
διαφωνω δλδ με τον τροπο που υπολογιζεις τον χρονο αποκαταστασης,δες σελιδα 388 και σχεση 9.2.17
Νομιζω οτι αυτον τον τυπο π τον χρησιμοποιουμε πλεον παντου και εχει γινει σουπα για το Ts δλδ ts=4,16/a περισσοτερο ισχυει για ενα συστημα που εχει πολλους πολους. Εκτος εαν το σκεφτεσαι εσυ τωρα ετσι,γιατι υπολογισες το ζ και ειδες οτι ειναι μικροτερο απο 0,95 αρα και χρησιμοποιεις τον τυπο απο την σελις 388.Εγω νμζω γενικα οτι για ενα παρονομαστη του στυλ s^2+2ζωn+ωn^2 o χρονος αποκαταστασης ειναι ts=4,16/ζωn.Tι λετε?
Κι εγω ετσι νομιζω ειναι. Για συστημα δευτερης ταξης που μπορεις να βρεις τον παρονομαστη σε μορφη s^2+2ζωn+ωn^2 νομιζω κι εγω οτι απο εδω πρεπει να πας. Μπορει με μεγαλη προσεγγιση τα αποτελεσματα να ειναι ιδια. Αν θυμαμαι καλα καπου λεει οτι το 4,16/a ισχυει με μεγαλη προσεγγιση.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 18:37:14 pm
Εχω ενα θεματακι στο 3 του ΣΕΠΤ 2012:
στο β ερωτημα για να βρω το περιθωριο κερδους θελω να βρω που η φαση γινεται -180 να παρω το ω και να υπολογισω το μετρο της
συναρτησης μεταφορας. Αλλα οταν βαζω αναλογικο ελεγκτη (με θετικο k) το διαγραμμα bode φασης δεν μεταβαλλεται ετσι? Αρα η φαση θα γινεται -180 στο
ω που εχω βρει απο το πρωτο ερωτημα. Το οποιο μηπως μπορει κανεις να μου πει ποσο το εχει βγαλει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 28, 2014, 19:01:22 pm
για τον σεπτεμβριο του 9 το πρωτο θεμα τι εχετε να πειτε??τελικα τι κανουμε σε περιπτωση που ζηταει α πολο και ναναι ευσταθες το συστημα.?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 28, 2014, 19:06:55 pm
Οταν κρατάω κυρίαρχους πόλους για να βρώ Ts/Tp απο τη νεά 2ης τάξης που προκύπτει, τα κέρδη απο τους πόλους που δεν χρησιμοποιώ πρέπει να τα συνυπολογίσω ή τα αγνοώ;
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
πχ Αug 2010
2125
Hk(s)=-----------------------------------------------
(s+2-3i) (s+2+3i) (s+20-5i) (s+20+5i)
2125
Hk1s)=------------------------ ; Ts=4.16/2
(s+2-3i) (s+2+3i)
xe: s^2+4s+13 , ωn=sqrt(13) ζ=2/sqrt(13) -> Tp=pi/3
Μια λυση που εχω εγω,τα συνυπολογιζει.Εννοεις επειδη κανεις προσεγγιση κυριου πολου ας πουμε,αν το αγνοεις τελειως η οχι.Στο βιβλιο παντως σελιδα 191 το συνυπολογιζει ας πουμε παρολο που ο πολος ειναι 10 φορες μεγαλυτερος απο τον αλλον.Οντως,ξερει κανεις πιο συγκεκριμενα να απαντησει?
ρε συ επηρεαζει το χρονο αποκαταστασης αφου αναλογα με το τι κερδος θα εχεις στον αριθμητη αλλαζει και η τιμη του ωn αρα και του χρονο αποκαταστασης.
διαφωνω δλδ με τον τροπο που υπολογιζεις τον χρονο αποκαταστασης,δες σελιδα 388 και σχεση 9.2.17
Νομιζω οτι αυτον τον τυπο π τον χρησιμοποιουμε πλεον παντου και εχει γινει σουπα για το Ts δλδ ts=4,16/a περισσοτερο ισχυει για ενα συστημα που εχει πολλους πολους. Εκτος εαν το σκεφτεσαι εσυ τωρα ετσι,γιατι υπολογισες το ζ και ειδες οτι ειναι μικροτερο απο 0,95 αρα και χρησιμοποιεις τον τυπο απο την σελις 388.Εγω νμζω γενικα οτι για ενα παρονομαστη του στυλ s^2+2ζωn+ωn^2 o χρονος αποκαταστασης ειναι ts=4,16/ζωn.Tι λετε?
Κι εγω ετσι νομιζω ειναι. Για συστημα δευτερης ταξης που μπορεις να βρεις τον παρονομαστη σε μορφη s^2+2ζωn+ωn^2 νομιζω κι εγω οτι απο εδω πρεπει να πας. Μπορει με μεγαλη προσεγγιση τα αποτελεσματα να ειναι ιδια. Αν θυμαμαι καλα καπου λεει οτι το 4,16/a ισχυει με μεγαλη προσεγγιση.
Εμείς ξέρουμε οτι πρεπει να είναι
Wn^2
--------------------------------
S^2 + 2Z* Wn S + Wn^2
Για να παρουμε τα Τ=4/ζ Wn
Αν δεν το φέρω στη παραπανω μορφή ισχύει;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 19:13:04 pm
Αν ο παρονομαστης ειναι σ'αυτην την μορφη ισχυει. Ο ορος μπροστα απο το s^2 πρεπει να ειναι μοναδα για να παρεις τον τυπο. Ο αριθμητης νομιζω δεν σε νοιαζει, αλλα δεν ειμαι και σιγουρος ας επιβεβαιωσει καποιος.
Θελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
Θελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 19:15:07 pm
για τον σεπτεμβριο του 9 το πρωτο θεμα τι εχετε να πειτε??τελικα τι κανουμε σε περιπτωση που ζηταει α πολο και ναναι ευσταθες το συστημα.?
Βρισκεις το κεντρο των ασυμπτωτων (λογικα θα ειναι δυο) με γωνεις +90, -90 και για να ειναι ευσταθες θες να ειναι το κεντρο αρνητικο, απο εκει βγαζεις μια τιμη για το α. Σε καλυψα?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 28, 2014, 19:26:27 pm
για τον σεπτεμβριο του 9 το πρωτο θεμα τι εχετε να πειτε??τελικα τι κανουμε σε περιπτωση που ζηταει α πολο και ναναι ευσταθες το συστημα.?
Βρισκεις το κεντρο των ασυμπτωτων (λογικα θα ειναι δυο) με γωνεις +90, -90 και για να ειναι ευσταθες θες να ειναι το κεντρο αρνητικο, απο εκει βγαζεις μια τιμη για το α. Σε καλυψα?
αυτο ενταξει οκ.εγω λεω αν πας στο δευτερο ερωτημα που σου λεει να βρεις τιμη για το α ωστε να εχεις χρονο αποκαταστασης μικροτερο απο κατι.επισυναπτω μια λυση που εχω εδω και θελω να μ πει καποιος πως σκατα επρεπε να ξερει κανεις αν εδινε εκεινη την εξεταστικη εαν ο ΓΤΡ εβγαινε ετσι και οχι αλλιως...
για να βρει την τιμη του πολου α ,λεει ας πουμε σ>= 4,16/ts το οποιο ts το δινει στην εκφωνηση .Βρισκει το σ και μετα το εξισωνει με την τιμη του ΟΑ στην οποια η μονη παραμετρος πλεον ειναι ο πολος α. Απο πανω απτην λυση φαινεται ο ΓΤΡ που σχεδιαζει εφοσον θετει το α ισον με 3,5 ας πουμε.
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 28, 2014, 20:00:49 pm
Αν ο παρονομαστης ειναι σ'αυτην την μορφη ισχυει. Ο ορος μπροστα απο το s^2 πρεπει να ειναι μοναδα για να παρεις τον τυπο. Ο αριθμητης νομιζω δεν σε νοιαζει, αλλα δεν ειμαι και σιγουρος ας επιβεβαιωσει καποιος.
Θελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
Η ΣΜΚΒΘελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
k
Ηκ(s)=--------------------------------------
s(s+2)(s+4)+k
x.e s^3+6s^2 +8s+k
routh
K<48
gm*k<48
θέλω όμως
gm =10db => gm = 20^(10/20)=3.16
Κ<48/3,16
Κ<15,18
απο Κ 9+ βγαζεις απόσβεση διαταραχων μεγαλύερη η ίση απο 20dB
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 20:31:14 pm
Αν ο παρονομαστης ειναι σ'αυτην την μορφη ισχυει. Ο ορος μπροστα απο το s^2 πρεπει να ειναι μοναδα για να παρεις τον τυπο. Ο αριθμητης νομιζω δεν σε νοιαζει, αλλα δεν ειμαι και σιγουρος ας επιβεβαιωσει καποιος.
Θελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
Η ΣΜΚΒΘελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
k
Ηκ(s)=--------------------------------------
s(s+2)(s+4)+k
x.e s^3+6s^2 +8s+k
routh
K<48
gm*k<48
θέλω όμως
gm =10db => gm = 20^(10/20)=3.16
Κ<48/3,16
Κ<15,18
απο Κ 9+ βγαζεις απόσβεση διαταραχων μεγαλύερη η ίση απο 20dB
Thank you! :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 28, 2014, 20:35:38 pm
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
ποσα μηδενικά και πόσους πόλους έχεις; (δεν καταλαβαίνω στο σχημα στον αξονα τον Real τι έχεις) αν έχεις περισότερους πόλους απο μηδενικα
θα έχεις (Αριθμος_πόλων) - (Αριθμός_μηδενικών) που καταλήγουν στο άπειρο κατα μήκος ασύμπτωτων
αυτοι που περισσεύουν καταλήγουν στα μηδενικο/α πανω στον Real
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 20:45:54 pm
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
ποσα μηδενικά και πόσους πόλους έχεις; (δεν καταλαβαίνω στο σχημα στον αξονα τον Real τι έχεις) αν έχεις περισότερους πόλους απο μηδενικα
θα έχεις (Αριθμος_πόλων) - (Αριθμός_μηδενικών) που καταλήγουν στο άπειρο κατα μήκος ασύμπτωτων
αυτοι που περισσεύουν καταλήγουν στα μηδενικο/α πανω στον Real
Δεν ειναι τοσο απλο τελικα, εκτος αν κολλησα καπου. Αμα κανεις το σχημα και πας να το σχεδιασης θα το δεις κι εσυ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 28, 2014, 21:13:44 pm
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
ποσα μηδενικά και πόσους πόλους έχεις; (δεν καταλαβαίνω στο σχημα στον αξονα τον Real τι έχεις) αν έχεις περισότερους πόλους απο μηδενικα
θα έχεις (Αριθμος_πόλων) - (Αριθμός_μηδενικών) που καταλήγουν στο άπειρο κατα μήκος ασύμπτωτων
αυτοι που περισσεύουν καταλήγουν στα μηδενικο/α πανω στον Real
Δεν ειναι τοσο απλο τελικα, εκτος αν κολλησα καπου. Αμα κανεις το σχημα και πας να το σχεδιασης θα το δεις κι εσυ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 28, 2014, 21:58:30 pm
Αν ο παρονομαστης ειναι σ'αυτην την μορφη ισχυει. Ο ορος μπροστα απο το s^2 πρεπει να ειναι μοναδα για να παρεις τον τυπο. Ο αριθμητης νομιζω δεν σε νοιαζει, αλλα δεν ειμαι και σιγουρος ας επιβεβαιωσει καποιος.
Θελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
Η ΣΜΚΒΘελω βοηθεια στον τροπο λυσης του τριτου θεματος τον σεπτεμβριο του 2012! :(
k
Ηκ(s)=--------------------------------------
s(s+2)(s+4)+k
x.e s^3+6s^2 +8s+k
routh
K<48
gm*k<48
θέλω όμως
gm =10db => gm = 20^(10/20)=3.16
Κ<48/3,16
Κ<15,18
απο Κ 9+ βγαζεις απόσβεση διαταραχων μεγαλύερη η ίση απο 20dB
Και στο α ερωτημα το περιθωριο κερδους ποσο το βρηκες?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 28, 2014, 22:19:52 pm
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
ποσα μηδενικά και πόσους πόλους έχεις; (δεν καταλαβαίνω στο σχημα στον αξονα τον Real τι έχεις) αν έχεις περισότερους πόλους απο μηδενικα
θα έχεις (Αριθμος_πόλων) - (Αριθμός_μηδενικών) που καταλήγουν στο άπειρο κατα μήκος ασύμπτωτων
αυτοι που περισσεύουν καταλήγουν στα μηδενικο/α πανω στον Real
δεν ειναι τοσο απλο οσο το λες γενικα ρε συ.Να ας πουμε εγω μιλαω τωρα για την συναρτηση
A(s)=(s+4)(s+6)/s(s+a)((s+4,5)^2+25)
Πες οτι το α για καποιο λογο απο τα παραπανω ερωτηματα βγαινει 3,5.Σου επισυναπτω παλι τον ΓΤΡ ετσι οπως πιστευω εγω οτι ειναι .ΤΟ ΟΑ ΕΙΝΑΙ ΣΤΟ -2,25 ΚΑΙ ΟΧΙ ΕΚΕΙ Π ΔΕΙΧΝΕΙ ΑΥΤΟ ΤΟ ΣΧΗΜΑ.προσπαθησε να το κανεις και μονος σου και προσπαθησε να μ εξηγησεις γιατι οι κλαδοι που παν στο απειρο ξεκιναν απο τους μιγαδικους πολους και οχι απο τους πραγματικους?
Εγω αυτο π σκεφτομαι ειναι οτι για να ξεκιναν απο τους πραγματικους πολους ,πρεπει το σημειο αποσχισης να συμπεσει με το ΟΑ,για να ικανοποιειται η συμμετρια του γεωμετρικου τοπου με τον αξονα χ και για να ικανοποιουνται και οι ασυμπτωτες.
Αλλη αιτιολογηση η κανονας που να εχει επισημανει στην ταξη και να μην το ξερω υπαρχει?Του στυλ κατι με τους μιγαδικους πολους και το απειρο ας πουμε?...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 00:00:07 am
Ως προς ποιον αξονα πρεπει να ειναι συμμετρικος ο ΓΤΡ; Το εχω ξεχασει τελειως!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 29, 2014, 00:12:14 am
ως προς τον αξονα Χ.
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 29, 2014, 01:13:04 am
Πως σκατα ξερει οτι οι κλαδοι απο τους μιγαδικους πανε στο απειρο και οι αλλοι δυο πανε στα μηδενικα????Αυτο το πραμα αν ΔΕΝ κανεις με ματλαμπ,μπορεις να το καταλαβεις καπως???
ποσα μηδενικά και πόσους πόλους έχεις; (δεν καταλαβαίνω στο σχημα στον αξονα τον Real τι έχεις) αν έχεις περισότερους πόλους απο μηδενικα
θα έχεις (Αριθμος_πόλων) - (Αριθμός_μηδενικών) που καταλήγουν στο άπειρο κατα μήκος ασύμπτωτων
αυτοι που περισσεύουν καταλήγουν στα μηδενικο/α πανω στον Real
δεν ειναι τοσο απλο οσο το λες γενικα ρε συ.Να ας πουμε εγω μιλαω τωρα για την συναρτηση
A(s)=(s+4)(s+6)/s(s+a)((s+4,5)^2+25)
Πες οτι το α για καποιο λογο απο τα παραπανω ερωτηματα βγαινει 3,5.Σου επισυναπτω παλι τον ΓΤΡ ετσι οπως πιστευω εγω οτι ειναι .ΤΟ ΟΑ ΕΙΝΑΙ ΣΤΟ -2,25 ΚΑΙ ΟΧΙ ΕΚΕΙ Π ΔΕΙΧΝΕΙ ΑΥΤΟ ΤΟ ΣΧΗΜΑ.προσπαθησε να το κανεις και μονος σου και προσπαθησε να μ εξηγησεις γιατι οι κλαδοι που παν στο απειρο ξεκιναν απο τους μιγαδικους πολους και οχι απο τους πραγματικους?
Εγω αυτο π σκεφτομαι ειναι οτι για να ξεκιναν απο τους πραγματικους πολους ,πρεπει το σημειο αποσχισης να συμπεσει με το ΟΑ,για να ικανοποιειται η συμμετρια του γεωμετρικου τοπου με τον αξονα χ και για να ικανοποιουνται και οι ασυμπτωτες.
Αλλη αιτιολογηση η κανονας που να εχει επισημανει στην ταξη και να μην το ξερω υπαρχει?Του στυλ κατι με τους μιγαδικους πολους και το απειρο ας πουμε?...
οι 2 κλαδοι θα ακολουθήσουν τις ασύμπτωτες και
οι άλλοι 2 κλαδοι ειναι πανω στον άξονα τον Real μεταξυ το (0,-3,5) και (-4,-6) Προφανως και πάνω σε αυτους τους κλαδους θα κινηθουν οι πόλοι του Πραγματιου άξονα προς τα μηδενικά του πραγματικου άξονα.
Δεδομένου οτι έχεις ασυνέχεια στον κλάδο και εχεις 2 μηδενικα αριστερα και 2 πολους δεξια αναμένεις να έχεις σημεια θλάσης Αφου πρέπει κάπως να φτάστουν οι πόλοι στον αλλο κλαδο. Αλλα η εξίσωση σου ειναι 5ου βαθμού (dk/ds) γιαυτο δεν σκας απλα τα μηδενικα σου πανε πανω στον real προσέγγιση κάνουμε ετσι και αλλιως!
το τι89 βέβαια το έλυσε και τα σημεια θλάσης ειναι στο -2,7 και -4,5 δηλαδη ενα σε κάθε κλάδο.
Δλδ οι πόλοι πανε στο -2,7 και κανουν αλμα μεχρι το -4,5 και απο εκει χωρίζονται στα 2 μηδενικά
Δες και τη matlab για να καταλάβεις
πάντα έχουμε τον πραγματικό άξονα ως άξονα συμμετρίας ,βοηθάει οταν κάνουμε σχήματα.
(http://i58.tinypic.com/scgr5s.jpg)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 29, 2014, 01:32:50 am
το εχω κεγω αυτο το σχημα.ξερω ποια ειναι η σωστη λυση.αλλα γιατι ΠΡΟΦΑΝΩΣ και οι πολοι στον real αξονα θα πανε στα μηδενικα?αυτο απο που το συμπεραινουμε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 29, 2014, 07:32:07 am
το εχω κεγω αυτο το σχημα.ξερω ποια ειναι η σωστη λυση.αλλα γιατι ΠΡΟΦΑΝΩΣ και οι πολοι στον real αξονα θα πανε στα μηδενικα?αυτο απο που το συμπεραινουμε?
μαθηματικά μπορώ να στο εξηγήσω αν πάρεις το
lim(χαρακτηριστικό πολυώνυμο)
Κ -> 00
δες 322-323 απο Πετρίδη.
αλλιώς διαισθητικά και εμπειρικά οι πόλοι πάνω στον real πάνε στα μηδενικά πάνω στον real
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sof_s on January 29, 2014, 15:28:15 pm
Στο θεέμα 2.δ Σεπτεμβρίου 2013 πως βγάζουμε το περιθώριο κέρδους; Εγώ έβαλα μηδενικό μ=5. Μετά βάζω ένα κέρδος Κ στην συνάρτηση ανοιχτού βρόγχου και κάνω Routh αλλά μου βγαίνει μια συνθήκη για το Κ να είναι θετικό και μία να είναι μικρότερο από έναν αρνητικό αριθμό. Κάνω κάτι λάθος; Και πότε το gm είναι άπειρο; Σε συστήματα 2ου βαθμού ή και αλλού;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 29, 2014, 16:17:06 pm
ως προς τον αξονα Χ.
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
αυτό με πολλές προσπάθειες και βλέποντας το αντίστοιχο τοπικ, απλα έβαλα μηδενικο s+3 για να απαλείψω τον πόλο, είναι η μόνη λυση για να βγαίνουν οι περιορισμοί (από ότι ελεγαν και στο τοπικ είχε δόσει λαθος προδιαγραφές)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mardi on January 29, 2014, 19:04:59 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 19:29:01 pm
ως προς τον αξονα Χ.
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
αυτό με πολλές προσπάθειες και βλέποντας το αντίστοιχο τοπικ, απλα έβαλα μηδενικο s+3 για να απαλείψω τον πόλο, είναι η μόνη λυση για να βγαίνουν οι περιορισμοί (από ότι ελεγαν και στο τοπικ είχε δόσει λαθος προδιαγραφές)
Ειχαμε και με αλλον την ιδια απορια για τα θεματα του Γεναρη του 11.
Τσεκαρε εδω ---> https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488 (https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: mar-m on January 29, 2014, 20:17:16 pm
Στο πρώτο θέμα του Φεβρουαρίου 2005 καμιά ιδέα για το β??Επίσης,το περιθώριο κέρδους στο α ερώτημα πώς βγαίνει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kodi on January 29, 2014, 20:56:49 pm
Στο θέμα 2ο Σεπτ 2013 για το ερώτημα γ, με την προσθήκη μηδενικού θεωρούμε ότι το ωc του προηγούμενου ερωτήματος είναι ίδιο; ή πρέπει να βρούμε νέο ωc και μετά το περιθώριο φάσης;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 29, 2014, 20:58:11 pm
Στο θέμα 2ο Σεπτ 2013 για το ερώτημα γ, με την προσθήκη μηδενικού θεωρούμε ότι το ωc του προηγούμενου ερωτήματος είναι ίδιο; ή πρέπει να βρούμε νέο ωc και μετά το περιθώριο φάσης;
καινούργιο ωcTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kodi on January 29, 2014, 21:02:35 pm
Στο θέμα 2ο Σεπτ 2013 για το ερώτημα γ, με την προσθήκη μηδενικού θεωρούμε ότι το ωc του προηγούμενου ερωτήματος είναι ίδιο; ή πρέπει να βρούμε νέο ωc και μετά το περιθώριο φάσης;
καινούργιο ωcκαι το καινούργιο ωc θα είναι συναρτήσει του μ έτσι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 29, 2014, 21:08:26 pm
λογικά ναι , εκτός αν απλοποιείτε το μ κάπου.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kodi on January 29, 2014, 21:10:21 pm
λογικά ναι , εκτός αν απλοποιείτε το μ κάπου.
Οκ ευχαριστώ! ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 29, 2014, 21:16:53 pm
λογικά ναι , εκτός αν απλοποιείτε το μ κάπου.
Οκ ευχαριστώ! ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Falergon on January 29, 2014, 21:51:04 pm
Πως βρίσκεις εύρος ζώνης όπως ζητάει στο θέμα 1 του Σεπτεμβρίου 2012?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 29, 2014, 22:06:29 pm
Πως βρίσκεις εύρος ζώνης όπως ζητάει στο θέμα 1 του Σεπτεμβρίου 2012?
Αφού σου δίνει διάγραμμα Bode κλειστού βρόχου το wb είναι εκεί που το Bode -3db από το |Hk(0)|, άρα εκεί που είναι 17db. Στα 17db πέφτει από την τελευταία ευθεία που είναι -20log(ω/1000) (αφού περνάει από το 0db στο 1000rad/sec). Οπότε βαζεις 17db=-20log(ωb/1000) και λύνεις ως προς ωb).
Εγώ θέλω να ρωτήσω για το θέμα 2γ του Σεπτ2013, που αναφέρατε πιο πάνω με το μηδενικό. Πως περίπου βγαίνει το μ και τι λογική ακολουθούμε, γιατί μου βγαίνουν κάτι ψιλοκουφές εξισώσεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 22:07:29 pm
Εγώ θέλω να ρωτήσω για το θέμα 2γ του Σεπτ2013, που αναφέρατε πιο πάνω με το μηδενικό. Πως περίπου βγαίνει το μ και τι λογική ακολουθούμε, γιατί μου βγαίνουν κάτι ψιλοκουφές εξισώσεις.
Kι εγω οτι να'ναι βγαζω, μπορει να καποιος να πει τον συλλογισμο?
λογικά ναι , εκτός αν απλοποιείτε το μ κάπου.
Οκ ευχαριστώ! ;)
Oταν υπολογιζω αρχικα το ωc gia to πρωτο ερωτημα δεν υπολογιζω τον πολο στο -20 γιατι απο το bode φαινεται οτι το ωc θα ειναι πριν το 20. Οταν προσθετω το μηδενικο για να
βρω το ωc πρεπει να υπολογισω ολους τους πολους? Υπαρχει κανενας πιο ευκολος τροπος να το κανω η πρεπει να υπολογιζω μετρα με ωc και μ μεσα?
Σορρυ για τις ερωτησεις αλλα με εχει παιδεψει πολυ το συγκεκριμενο θεμα!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 29, 2014, 22:11:32 pm
ως προς τον αξονα Χ.
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
αυτό με πολλές προσπάθειες και βλέποντας το αντίστοιχο τοπικ, απλα έβαλα μηδενικο s+3 για να απαλείψω τον πόλο, είναι η μόνη λυση για να βγαίνουν οι περιορισμοί (από ότι ελεγαν και στο τοπικ είχε δόσει λαθος προδιαγραφές)
Ειχαμε και με αλλον την ιδια απορια για τα θεματα του Γεναρη του 11.
Τσεκαρε εδω ---> https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488 (https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488)
αυτη λυση σε αυτο το λινκ ειναι σωστη?νμζω δλδ οτι ειναι σωστη γιατι κεγω καπως ετσι το σκεφτηκα να το λυσω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 22:15:33 pm
ως προς τον αξονα Χ.
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
Να ρωτησω εγω κατι αλλο τωρα.?Εχει δει κανεις το θεμα 2ο του Γεναρη 2011? Τι ελεγκτη πρεπει να βαλουμε εκει?Γιατι εχω μπερδευτει λιγο με την δευτερη προδιαγραφη που λεει οτι πρεπει ts<1s.
Μπορει κανεις να με βοηθησει?
αυτό με πολλές προσπάθειες και βλέποντας το αντίστοιχο τοπικ, απλα έβαλα μηδενικο s+3 για να απαλείψω τον πόλο, είναι η μόνη λυση για να βγαίνουν οι περιορισμοί (από ότι ελεγαν και στο τοπικ είχε δόσει λαθος προδιαγραφές)
Ειχαμε και με αλλον την ιδια απορια για τα θεματα του Γεναρη του 11.
Τσεκαρε εδω ---> https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488 (https://www.thmmy.gr/smf/index.php?topic=46369.msg810488#msg810488)
αυτη λυση σε αυτο το λινκ ειναι σωστη?νμζω δλδ οτι ειναι σωστη γιατι κεγω καπως ετσι το σκεφτηκα να το λυσω.
Τι να σου πω, κι εγω ετσι πηγα να το κανω και ειχα το ιδιο προβλημα.
Και τα αλλα θεματα με παρομοιες προδιαγραφες ετσι τα ελυσα και μου βγαιναν καλα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 22:42:09 pm
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 29, 2014, 23:24:04 pm
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 29, 2014, 23:44:22 pm
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
Eυχαριστω ρε, Exomag! Καλο ακουγεται, εχεις και αιτιολογηση, εμενα με επεισε και το κραταω! Thanks! :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: nash on January 30, 2014, 00:10:23 am
μπορει καποιος να μου πει πως θα βρω απο την γραφικη παρασταση την H(s)και τα w1,w2 , wb??(1ο θεμα σεπτ 2012)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 30, 2014, 00:41:10 am
μπορει καποιος να μου πει πως θα βρω απο την γραφικη παρασταση την H(s)και τα w1,w2 , wb??(1ο θεμα σεπτ 2012)
To μόνο που χρειάζεσαι είναι ότι η ευθεία στο λογαριθμικό είναι y = K log(w/w0) με K την κλίση της, w0 την συχνότητα που τέμνει τον άξονα των συχνοτήτων (δηλ y=0dB). Οπότε σου δίνει σημεία που επαληθεύουν οι ευθείες. πχ για το πρώτο y=+20log(w/w0) που περνάει από το (1 rad/sec ,20 dB) άρα 20 = 20log(1/w0) και βρίσκεις το w0. Αυτή περνάει και από το (w1, 33,97), οπότε 33,97 = 20log(w1/w0) και βρίσκεις το w1 αφού ξέρεις το w0 πια.
Για το εύρος ζώνης βλέπε παραπάνω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 30, 2014, 00:51:15 am
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
δεδομένου οτι δεν έχουμε κριτήρια ή περιορισμούς που πρέπει να καλύψουμε
δεν μπορούμε να υποθέσουμε οτι για το ίδιο Wc θελω απλα να αυξήσω το περιθώριο φάσης κατα Θ
δλδ έστω οτι πριν ειχαμε βρει περιθώριο φάσης 10
τώρα θελω 40
επομένως πρεπει το <(s+μ)=30
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 30, 2014, 01:00:59 am
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
Eυχαριστω ρε, Exomag! Καλο ακουγεται, εχεις και αιτιολογηση, εμενα με επεισε και το κραταω! Thanks! :)
πάντως διαφωνώ στο μ=0 αλλαζεις τελείως τη συνάρτηση μεταφορας ,αλλαζεις τον τυπο αυτης (πρακτικα είναι αλλο κύκλωμα)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 30, 2014, 01:02:30 am
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
Eυχαριστω ρε, Exomag! Καλο ακουγεται, εχεις και αιτιολογηση, εμενα με επεισε και το κραταω! Thanks! :)
πάντως διαφωνώ στο μ=0 αλλαζεις τελείως τη συνάρτηση μεταφορας ,αλλαζεις τον τυπο αυτης (πρακτικα είναι αλλο κύκλωμα)
Συν το ότι δεν ξέρω αν μπορείς να απλοποιήσεις μη ευσταθείς πόλους (γιατί είναι πάνω στον φανταστικό). Όλα αυτά λύνονται αν πάρεις μηδενικό κοντά στο 0, πχ 0,5.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: trelakis on January 30, 2014, 01:03:23 am
παιδιά στα ΙΑΝ 2010 θέμα 3 (τα έχει λυμένα στο thmmy downloads) για τον χρόνο αποκατάστασης ts<=3s <=> -σ<=- 1.387..όμως την ο περιορισμός αυτός ισχύει για πόλους ΣΜΚΒ..αυτός παίρνει τον περιορισμό αυτό για ΣΜΑΒ και λέει b=5..λάθος δεν είναι να το χρησιμοποιήσω το ts με αυτόν τον τρόπο ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 30, 2014, 01:03:34 am
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
δεδομένου οτι δεν έχουμε κριτήρια ή περιορισμούς που πρέπει να καλύψουμε
δεν μπορούμε να υποθέσουμε οτι για το ίδιο Wc θελω απλα να αυξήσω το περιθώριο φάσης κατα Θ
δλδ έστω οτι πριν ειχαμε βρει περιθώριο φάσης 10
τώρα θελω 40
επομένως πρεπει το <(s+μ)=30
Δεν είναι σωστό αυτό, γιατί το μ επηρεάζει και το ωc!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 30, 2014, 01:04:33 am
Μπορει καποιος να μου δωσει τα φωτα του στα δυο τελευταια ερωτηματα απο το δευτερο Θεμα του Σεπτεμβριου του 2013? :(
Θα σου πω εγώ πως το σκέφτηκα (δεν είναι η καλύτερη λύση, αλλά είναι αποδεκτή).
Ο ολοκληρωτής 1/s δίνει -90ο σε όλες τις συχνότητες. Οπότε μπορείς να βάλεις μ = 0, προκειμένου να τον απαλείψεις. Στη συνάρτηση που μένει, βρίσκεις το περιθώριο φάσης και βλέπεις ότι είναι λίγο μεγαλύτερο από 40ο. Άρα ικανοποιείται η προδιαγραφή σου ;)
Eυχαριστω ρε, Exomag! Καλο ακουγεται, εχεις και αιτιολογηση, εμενα με επεισε και το κραταω! Thanks! :)
πάντως διαφωνώ στο μ=0 αλλαζεις τελείως τη συνάρτηση μεταφορας ,αλλαζεις τον τυπο αυτης (πρακτικα είναι αλλο κύκλωμα)
Η Δουλγέρη σε παράδειγμα, πάντως, έχει τύχει να απλοποιήσει πόλο μέσω ενός μεταβλητού μηδενικού.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: TrueForce on January 30, 2014, 02:24:29 am
Στο θεμα 1 β) (σεπτεμβρης 13) ποσο βρηκατε το περιθωριο κερδους; Εννοεί τις τιμές που μπορεί να πάρει το κ;
edit ακυρη ερωτηση, G=ko/k
edit ακυρη ερωτηση, G=ko/k
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 30, 2014, 10:41:09 am
Στο θεμα 1 β) (σεπτεμβρης 13) ποσο βρηκατε το περιθωριο κερδους; Εννοεί τις τιμές που μπορεί να πάρει το κ;
edit ακυρη ερωτηση, G=ko/k
edit ακυρη ερωτηση, G=ko/k
Αν θεωρήσεις πως το περιθώριο κέρδους είναι ως προς Κ, βγαίνει gm = 3450. Αλλιώς, θα βγει gm = 3450/K.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mr K on January 30, 2014, 12:40:59 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ak1s on January 30, 2014, 13:31:35 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
Αν κάποιος το έχει κάνει θα βοηθούσε πολύ αν μας εξηγούσε. Πάντως αν χρησιμοποιήσεις τη συνθήκη βγαίνει ότι μ<13,36. Αν διαλέξεις ένα μηδενικό και προσπαθήσεις να βρεις σημείο απόσχισης
βγάζει μια εξίσωση τριτοβάθμια που δεν απλοποιείται, Μήπως θα μπορούσε να απαλειφθεί ο πόλος -18 από την εξίσωση; Η απλά διαλέγεις ένα μηδενικό το οποίο να βρίσκεται μέσα στο ΓΤΡ και απλά
επειδή οι ασύμπτωτες έχουν +-90 το κέρδος σου είναι άπειρο και σταματάς εκεί;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: TrueForce on January 30, 2014, 14:29:54 pm
Στο θεμα 1 β) (σεπτεμβρης 13) ποσο βρηκατε το περιθωριο κερδους; Εννοεί τις τιμές που μπορεί να πάρει το κ;
edit ακυρη ερωτηση, G=ko/k
edit ακυρη ερωτηση, G=ko/k
Αν θεωρήσεις πως το περιθώριο κέρδους είναι ως προς Κ, βγαίνει gm = 3450. Αλλιώς, θα βγει gm = 3450/K.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mr K on January 30, 2014, 14:50:31 pm
Στο θεμα 1 β) (σεπτεμβρης 13) ποσο βρηκατε το περιθωριο κερδους; Εννοεί τις τιμές που μπορεί να πάρει το κ;
edit ακυρη ερωτηση, G=ko/k
edit ακυρη ερωτηση, G=ko/k
Αν θεωρήσεις πως το περιθώριο κέρδους είναι ως προς Κ, βγαίνει gm = 3450. Αλλιώς, θα βγει gm = 3450/K.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mr K on January 30, 2014, 14:52:08 pm
Νέα ερώτηση: στο δ του θεματος 2 του σεπτεμβρη 2013 πώς βρίσκουμε περιθώριο κέρδους, δηλαδη ξερω οτι ειναι στο ω1 οπου το διαγραμμα φάσης ειναι -180 αλλα πως βρίσκω το ω1;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on January 30, 2014, 15:42:25 pm
Για το θέμα 2 του φεβρουαρίου 2013 έχει κανείς αποτελέσματα? εγώ βρίσκω μ<21.06 κ*μ>=1296.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Captain Mixos on January 30, 2014, 17:12:52 pm
σωστός εισαι.. Η δουλγερη στην ταξη πήρε μ=8 και κ=200
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: lampthras on January 30, 2014, 17:26:38 pm
Σεπ 2012 θέμα β που έχει ένα σύστημα με ΜΗ μοναδιαια αναδραση πώς βρίσκω ΓΤΡ; εχει καμια διαφορά;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Dealan on January 30, 2014, 17:33:33 pm
Καμία διαφορά, βρίσκεις την L(s) και συνεχίζεις κανονικά.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sΚονταριτσα on January 30, 2014, 17:33:48 pm
Νέα ερώτηση: στο δ του θεματος 2 του σεπτεμβρη 2013 πώς βρίσκουμε περιθώριο κέρδους, δηλαδη ξερω οτι ειναι στο ω1 οπου το διαγραμμα φάσης ειναι -180 αλλα πως βρίσκω το ω1;
για να βρεις το περιθωριο κερδους σε αυτο το θεμα,απλα θεωρεις οτι εισαι σε πολυ μεγαλες συχνοτητες,γιατι ουτως η αλλως το περιθωριο κερδους βρισκεται οταν το bode φασης εχει ξεφυγει σε γωνιες μεγαλυτερες απο τις 180 (σε απολυτη τιμη).Οποτε θα θεσεις τωρα εσυ προσεγγιστικα οτι ολες οι συχνοτητες σου εχουν παει 10 φορες η τιμη τους.Δλδ ουσιαστικα εισαι σε πολυ μεγαλες τιμες της συχνοτητας.Οι συχνοτητες ειναι ουσιαστικα οι πολο και τα μηδενικα της συναρτησης.
Για το Bode φασης,αν δεις και τις σημειωσεις του Σταμουλη για περιοχες τιμων συχνοτητων οι οποιες ειναι 10 φορες η τιμη τους ,οι πολοι δινουν -90 μοιρες φαση και τα μηδενικα δινουν +90 μοιρες φαση.
Επομενως με αυτην την λογικη για αυτο το θεμα,μετα την προσθεση του μηδενικου ,εχεις +90 απο το μηδενικο,-90 απο τον πολο στο μηδεν και αλλα -180 απο τους αλλους δυο πολους.Επομενως αν τα αθροισεις αυτα,φτανεις προσεγγιστικα τις -180 μοιρες για πολυ μεγαλες συχνοτητες αλλα δεν τις ξεπερνας ΠΟΤΕ ομως.Αρα μπορεις να πεις προσεγγιστικα οτι το περιθωριο κερσους ειναι απειρο.Καταλαβες?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: et3rn1ty on January 30, 2014, 18:03:15 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
(με κάθε επιφύλαξη, μπορεί να λέω μπούρδες :D )
Από τον τύπο που είπες 4/σ παίρνεις ότι σ<8. Το σ είναι το πραγματικό μέρος του μικρότερου πόλου της Α(s) (αυτό μέχρι να βρω πού το λέει ο Πετρίδης μου πήρε λίγο χρόνο, τελικά είναι στη σελίδα 389 με bold). Οπότε θέλεις να συμπεριλαμβάνονται στον ΓΤΡ τα σημεία του άξονα μετά το -8 (και το -8 συμπεριλαμβάνεται). Και αυτό το πετυχαίνεις βάζοντας το 0 κάπου ώστε το -8 να έχει δεξιά του συνολικά 3 μηδενικά και πόλους. Δηλαδή εγώ το έβαλα στο -8 γιατί το -7 ήταν πιασμένο :P.
Απλώς δεν είμαι σίγουρος γιατί από το βιβλίο δεν κατάλαβα αν αυτός ο τύπος (ts=4/σ) ισχύει και όταν ζ > 1, δηλαδή όταν το σύστημα έχει πραγματικούς πόλους. Πρέπει να ισχύει, αλλά το κεφάλαιο στο οποίο μας δίνει τον τύπο ο Πετρίδης μιλάει για συστήματα με φανταστικούς πόλους κυρίως...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: mar-m on January 30, 2014, 18:36:57 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Μπορείς να εξηγήσεις λίγο πώς το βρήκες 0.067?Γιατί και εγώ 1.71 το βρίσκω και δεν ξέρω τι κάνω λάθος...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 30, 2014, 18:44:10 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
(με κάθε επιφύλαξη, μπορεί να λέω μπούρδες :D )
Από τον τύπο που είπες 4/σ παίρνεις ότι σ<8. Το σ είναι το πραγματικό μέρος του μικρότερου πόλου της Α(s) (αυτό μέχρι να βρω πού το λέει ο Πετρίδης μου πήρε λίγο χρόνο, τελικά είναι στη σελίδα 389 με bold). Οπότε θέλεις να συμπεριλαμβάνονται στον ΓΤΡ τα σημεία του άξονα μετά το -8 (και το -8 συμπεριλαμβάνεται). Και αυτό το πετυχαίνεις βάζοντας το 0 κάπου ώστε το -8 να έχει δεξιά του συνολικά 3 μηδενικά και πόλους. Δηλαδή εγώ το έβαλα στο -8 γιατί το -7 ήταν πιασμένο :P.
Απλώς δεν είμαι σίγουρος γιατί από το βιβλίο δεν κατάλαβα αν αυτός ο τύπος (ts=4/σ) ισχύει και όταν ζ > 1, δηλαδή όταν το σύστημα έχει πραγματικούς πόλους. Πρέπει να ισχύει, αλλά το κεφάλαιο στο οποίο μας δίνει τον τύπο ο Πετρίδης μιλάει για συστήματα με φανταστικούς πόλους κυρίως...
Βασικά θες οι πόλοι της συνάρτησης κλειστού βρόγχου να έχουν πραγματικό μετά το 8 (που φαίνεται από το ΓΤΡ που κάνεις στην ανοικτού βρόγχου. Απλά ο ΓΤΡ δείχνει πως συμπεριφέρονται οι πόλοι της κλειστού βρόγχου). Δηλαδή στο ΓΤΡ θες για μεγάλα κέρδη (κ->οο) να είσαι μετά το 8. Εγώ νομίζω ότι στο θέμα αυτό βάζεις το μηδενικό στο -5 και απαλείφεις τον αντίστοιχο πόλο. Οπότε αν κάνεις στα γρήγορα νέο ΓΤΡ, έχεις δύο πόλους στο -18 και -7, όπου βρίσκεις σημείο απόσχισεις -10 και φεύγουν οι πόλοι κάθετα προς το άπειρο. Οπότε για μεγάλα Κ οι πόλοι του κλειστού έχουν ΠΑΝΤΑ πραγματικό -10 οπότε είσαι κομπλέ.
Ο τύπος 4/σ ισχύει για ζ<1 και για την ακρίβεια ισχύει για ζ πολύ κοντά στο 1 (~0,95, η χειρότερη περίπτωση). Δες τον τύπο πιο πάνω που το αποδεικνύει (σελ 388 πετρίδη). Για ζ>1 έχεις αρνητική ρίζα, οπότε δεν έχει φυσική σημασία όλο αυτό. Βασικά δεν έχεις πραγματικούς πόλους. Πραγματικούς πόλους έχει η Α(s). Οι κλειστού για μεγάλα κέρδη έχει μιγαδικούς. Οπότε το χρησιμοποιείς κανονικά.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Σαλτιμπάγκος on January 30, 2014, 18:44:31 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
(με κάθε επιφύλαξη, μπορεί να λέω μπούρδες :D )
Από τον τύπο που είπες 4/σ παίρνεις ότι σ<8. Το σ είναι το πραγματικό μέρος του μικρότερου πόλου της Α(s) (αυτό μέχρι να βρω πού το λέει ο Πετρίδης μου πήρε λίγο χρόνο, τελικά είναι στη σελίδα 389 με bold). Οπότε θέλεις να συμπεριλαμβάνονται στον ΓΤΡ τα σημεία του άξονα μετά το -8 (και το -8 συμπεριλαμβάνεται). Και αυτό το πετυχαίνεις βάζοντας το 0 κάπου ώστε το -8 να έχει δεξιά του συνολικά 3 μηδενικά και πόλους. Δηλαδή εγώ το έβαλα στο -8 γιατί το -7 ήταν πιασμένο :P
Απλώς δεν είμαι σίγουρος γιατί από το βιβλίο δεν κατάλαβα αν αυτός ο τύπος (ts=4/σ) ισχύει και όταν ζ > 1, δηλαδή όταν το σύστημα έχει πραγματικούς πόλους. Πρέπει να ισχύει, αλλά το κεφάλαιο στο οποίο μας δίνει τον τύπο ο Πετρίδης μιλάει για συστήματα με φανταστικούς πόλους κυρίως...
Αν βαλουμε το μ=5 κ απαλειφθει με τον πολο στον παρονομαστη τοτε εχουμε : 2κ/(s+7)(s+18)=2κ/s2+25s+126 και παρουμε τον τυπο ts=4,16/ζ*ωn οπου ζ*ωn=25/2 βρισκουμε ts=0.33
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Chester on January 30, 2014, 19:54:08 pm
Μπορει να εξηγησει καποιος πως βγαινουν οι γωνιες αναχωρησης αλγεβρικα; Π.χ στην ασκηση 36 αυτο το -153 πως προκυπτει ;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: c0ndemn3d on January 30, 2014, 19:55:02 pm
Παιδια 3ο ερώτημα 1ο θεμα σεπτ 2013: Ο χρονος αποκατάστασης ts <0.5. Ξέρω τον τύπο 4/σ αλλά έχω απορίες: πως σχετιζεται το συστημα ΚΛΕΙΣΤΟΥ βρόγχου, και τι σχέση έχει το σ με την τοποθετηση του 0 και που το βαλαμε τελικα το μ και γιατι;
(με κάθε επιφύλαξη, μπορεί να λέω μπούρδες :D )
Από τον τύπο που είπες 4/σ παίρνεις ότι σ<8. Το σ είναι το πραγματικό μέρος του μικρότερου πόλου της Α(s) (αυτό μέχρι να βρω πού το λέει ο Πετρίδης μου πήρε λίγο χρόνο, τελικά είναι στη σελίδα 389 με bold). Οπότε θέλεις να συμπεριλαμβάνονται στον ΓΤΡ τα σημεία του άξονα μετά το -8 (και το -8 συμπεριλαμβάνεται). Και αυτό το πετυχαίνεις βάζοντας το 0 κάπου ώστε το -8 να έχει δεξιά του συνολικά 3 μηδενικά και πόλους. Δηλαδή εγώ το έβαλα στο -8 γιατί το -7 ήταν πιασμένο :P
Απλώς δεν είμαι σίγουρος γιατί από το βιβλίο δεν κατάλαβα αν αυτός ο τύπος (ts=4/σ) ισχύει και όταν ζ > 1, δηλαδή όταν το σύστημα έχει πραγματικούς πόλους. Πρέπει να ισχύει, αλλά το κεφάλαιο στο οποίο μας δίνει τον τύπο ο Πετρίδης μιλάει για συστήματα με φανταστικούς πόλους κυρίως...
Αν βαλουμε το μ=5 κ απαλειφθει με τον πολο στον παρονομαστη τοτε εχουμε : 2κ/(s+7)(s+18)=2κ/s2+25s+126 και παρουμε τον τυπο ts=4,16/ζ*ωn οπου ζ*ωn=25/2 βρισκουμε ts=0.33
Αυτο ειναι λαθος;;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 30, 2014, 19:55:58 pm
Σωστό είναι
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: c0ndemn3d on January 30, 2014, 19:58:43 pm
Σωστό είναι
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
Είσαι κύριος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Σαλτιμπάγκος on January 30, 2014, 19:59:39 pm
Σωστό είναι
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
μου το είπε η Δουλγέρη
(αρκεί να αιτιολογήσεις και σωστά)
Είσαι κύριος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 30, 2014, 20:06:48 pm
Να πεις ρε παιδί μου πως βάζεις ένα μηδενικό πχ στη θέση ενός αργού πόλου για να τον απαλείψεις !
Για να έχεις γρήγορη απόσβεση!
Για να έχεις γρήγορη απόσβεση!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 30, 2014, 20:48:27 pm
Να πεις ρε παιδί μου πως βάζεις ένα μηδενικό πχ στη θέση ενός αργού πόλου για να τον απαλείψεις !
Για να έχεις γρήγορη απόσβεση!
Για να έχεις γρήγορη απόσβεση!
Γενικα ομως ο τυπος 4.16/σ < ts ισχυει προσεγγιστικα και για συστηματα μεγαλυτερου βαθμου ετσι? (Αγχωθηκα λιγο!)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: c0ndemn3d on January 30, 2014, 20:55:22 pm
(Αγχωθηκα λιγο!)
Άραξε.
Γενικα ομως ο τυπος 4.16/σ < ts ισχυει προσεγγιστικα και για συστηματα μεγαλυτερου βαθμου ετσι?
Σελίδα 389
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 30, 2014, 20:57:58 pm
(Αγχωθηκα λιγο!)
Άραξε.
Γενικα ομως ο τυπος 4.16/σ < ts ισχυει προσεγγιστικα και για συστηματα μεγαλυτερου βαθμου ετσι?
Σελίδα 389
Eυχαριστω! :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasl12 on January 30, 2014, 21:12:00 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
μπορεί κανεις να εξηγήσει πως το κάνουμε αυτό?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 30, 2014, 21:17:54 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
μπορεί κανεις να εξηγήσει πως το κάνουμε αυτό?
20log(12.5)+20log(1/0.1)
επίσης wc 0.067 δύσκολα 6, κατι βγαίνει
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pikachu93 on January 30, 2014, 21:20:37 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
μπορεί κανεις να εξηγήσει πως το κάνουμε αυτό?
20log(12.5)+20log(1/0.1)
επίσης wc 0.067 δύσκολα
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: et3rn1ty on January 30, 2014, 21:27:05 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
μπορεί κανεις να εξηγήσει πως το κάνουμε αυτό?
20log(12.5)+20log(1/0.1)
επίσης wc 0.067 δύσκολα 6, κατι βγαίνει
μιλάτε για διαφορετικά θέματα, το ωc του Ιανουαρίου 2013 βγαίνει όντως τόσο μικρό. Εσύ νομίζω μιλάς για Σεπτέμβριο 2013
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: mar-m on January 30, 2014, 21:28:45 pm
Θέμα 1β/ Ιανουάριος 2013
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Στο προσεγγιστικό διάγραμμα Bode το διάγραμμα μου ξεκινάει στα -3.5dB κέρδος και καταλήγει στα -46dB.
Που σημαίνει πως το κέρδος δεν είναι ίσο με 0dB σε κανένα σημείο του διαγράμματος, οπότε το ωc ποιό είναι?
Υπάρχει τρόπος να βρούμε το περιθώριο φάσης χωρίς το ωc ή έχω κάνει κάποιο λάθος στο Bode???
Όταν κάνω τους υπολογισμούς λογαριθμικά βγάζω ωc =1.71 rad/sec ??!!
Το έχει λύση κανείς να μου πει αποτελέσματα?
Προφανώς το ω από το οποίο ξεκίνησες να κάνεις το Bode δεν είναι αρκετά μικρό!
Στη συγκεκριμένη άσκηση το ωc έβγαινε περίπου 0.067, οπότε θα πρέπει να ξεκινήσεις το Bode από ακόμα πιο κάτω, προκειμένου να ξεκινήσεις από θετικά dB και να δεις ότι η γραφική παράσταση τέμενει τα 0dB κάπου.
Είχες δίκιο.Το είχα ξεκινήσει απο το 0.1 και δεν μου πήγε το μυαλό να το ξεκινήσω πιο κάτω. Έπρεπε απο το 0.01.
Thnx!
μπορεί κανεις να εξηγήσει πως το κάνουμε αυτό?
20log(12.5)+20log(1/0.1)
επίσης wc 0.067 δύσκολα 6, κατι βγαίνει
μιλάτε για διαφορετικά θέματα, το ωc του Ιανουαρίου 2013 βγαίνει όντως τόσο μικρό. Εσύ νομίζω μιλάς για Σεπτέμβριο 2013
μπορείς λίγο να πεις πώς το βρήκες??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: et3rn1ty on January 30, 2014, 21:45:56 pm
Λοιπόν από το Bode μπορείς να δεις ότι τέμνει τον άξονα πριν τα 0.1 και μετά τα 0.01 rad/s. Επειδή σε εκείνο το σημείο οι όροι (jω/3 +1), (jω/4 +1) κλπ έχουν μέτρο μηδέν (δεν συνεισφέρουν) μπορείς να τους παραβλέψεις, και άρα καταλήγεις στο
20log(15/224)=20logωc also known as ωc = 15/224 also known as ωc=0.067
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 30, 2014, 21:47:19 pm
Λοιπόν από το Bode μπορείς να δεις ότι τέμνει τον άξονα πριν τα 0.1 και μετά τα 0.01 rad/s. Επειδή σε εκείνο το σημείο οι όροι (jω/3 +1), (jω/4 +1) κλπ έχουν μέτρο μηδέν (δεν συνεισφέρουν) μπορείς να τους παραβλέψεις, και άρα καταλήγεις στο
20log(15/224)=20logωc also known as ωc = 15/224 also known as ωc=0.067
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: mar-m on January 30, 2014, 21:55:47 pm
Λοιπόν από το Bode μπορείς να δεις ότι τέμνει τον άξονα πριν τα 0.1 και μετά τα 0.01 rad/s. Επειδή σε εκείνο το σημείο οι όροι (jω/3 +1), (jω/4 +1) κλπ έχουν μέτρο μηδέν (δεν συνεισφέρουν) μπορείς να τους παραβλέψεις, και άρα καταλήγεις στο
20log(15/224)=20logωc also known as ωc = 15/224 also known as ωc=0.067
Aυτό πώς το βλέπεις?? :o
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: choco18 on January 30, 2014, 22:25:27 pm
σεπ. 2013 2β)
όταν ζητάει ακριβές περιθώριο φάσης του ΣΚΒ με μοναδιαία αρνητική ανάδραση παίρνω τον τύπο 180+<Α(jωc) όπου Α(jωc) ΣΑΒ;; βρίσκω το ωc=6.53 το αποτέλεσμα μου αν είναι σωστή η διαδικασία μου βγαίνει 13.4 μοίρες είναι σωστό;; ας με φωτίσει κάποιος!!
όταν ζητάει ακριβές περιθώριο φάσης του ΣΚΒ με μοναδιαία αρνητική ανάδραση παίρνω τον τύπο 180+<Α(jωc) όπου Α(jωc) ΣΑΒ;; βρίσκω το ωc=6.53 το αποτέλεσμα μου αν είναι σωστή η διαδικασία μου βγαίνει 13.4 μοίρες είναι σωστό;; ας με φωτίσει κάποιος!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on January 30, 2014, 22:37:41 pm
σεπ. 2013 2β)
όταν ζητάει ακριβές περιθώριο φάσης του ΣΚΒ με μοναδιαία αρνητική ανάδραση παίρνω τον τύπο 180+<Α(jωc) όπου Α(jωc) ΣΑΒ;; βρίσκω το ωc=6.53 το αποτέλεσμα μου αν είναι σωστή η διαδικασία μου βγαίνει 13.4 μοίρες είναι σωστό;; ας με φωτίσει κάποιος!!
ναι καπου εκει βγαίνειόταν ζητάει ακριβές περιθώριο φάσης του ΣΚΒ με μοναδιαία αρνητική ανάδραση παίρνω τον τύπο 180+<Α(jωc) όπου Α(jωc) ΣΑΒ;; βρίσκω το ωc=6.53 το αποτέλεσμα μου αν είναι σωστή η διαδικασία μου βγαίνει 13.4 μοίρες είναι σωστό;; ας με φωτίσει κάποιος!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 30, 2014, 23:02:47 pm
Γενικα οταν ζηταει ΓΤΡ πρεπει να κανουμε και για k<0 η απλα λεμε οτι ειναι συμμετρικο ως προς τον Χ-αξονα και τελος?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Fcoriolis on January 30, 2014, 23:04:35 pm
Νομίζω μόνο για κ>0 χρειάζεται εκτός αν διευκρινίζει.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 30, 2014, 23:15:12 pm
Νομίζω μόνο για κ>0 χρειάζεται εκτός αν διευκρινίζει.
Οk thanks!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: choco18 on January 31, 2014, 01:18:53 am
σεπ.2013 1β)
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Kodi on January 31, 2014, 01:22:46 am
σεπ.2013 1β)
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
όχι βρίσκεις τη ΣΜΚΒ και κάνεις κανονικά routh για αυτήν.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: choco18 on January 31, 2014, 01:39:05 am
ευχαριστώ!! το έκανα και βρίσκω κ<3450 μετα τι κανω;; θεωρω Κο=3450 και λεω οτι gm=3450/K;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 31, 2014, 01:59:41 am
σεπ.2013 1β)
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
πως βρισκω το περιθωριο κερδους;; πρεπει να κανω 1+Α(s) και μετα να κανω routh??
όχι βρίσκεις τη ΣΜΚΒ και κάνεις κανονικά routh για αυτήν.
Το ίδιο είναι, αφού η ΧΕ της ΣΜΚΒ είναι το 1+Α(s) = 0.
ευχαριστώ!! το έκανα και βρίσκω κ<3450 μετα τι κανω;; θεωρω Κο=3450 και λεω οτι gm=3450/K;;
Ναι.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Σαλτιμπάγκος on January 31, 2014, 02:21:10 am
ευχαριστώ!! το έκανα και βρίσκω κ<3450 μετα τι κανω;; θεωρω Κο=3450 και λεω οτι gm=3450/K;;
και σε ποια περιπτωση παιρνουμε 20log(k0)??Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: c0ndemn3d on January 31, 2014, 02:22:28 am
Μπορεί κάποιος να μου πει το θέμα 1 ιανουαρίου του 2011 για να σιγουρευτώ ότι το χω καταλάβει; συνοπτικά
άκυρο
άκυρο
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 31, 2014, 02:34:03 am
Μπορεί κάποιος να μου πει το θέμα 1 ιανουαρίου του 2011 για να σιγουρευτώ ότι το χω καταλάβει; συνοπτικά
Μαθημα 12 Ασκηση 1 ;)
Στην ιδια ασκηση μπορει καποιος να μου εξηγησει τι ειναι αυτη η βοηθητικη εξισωση που γραφει οταν θελει να βρει τις ριζες για k = 8. Δεν μπορουμε απλα να το βαλουμε στην χαρακτηριστικη εξισωση και να λυσουμε? Σορρυ αν ειναι χαζομαρα αυτο που ρωταω!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Jim D. Ace on January 31, 2014, 03:24:01 am
Στην ιδια ασκηση μπορει καποιος να μου εξηγησει τι ειναι αυτη η βοηθητικη εξισωση που γραφει οταν θελει να βρει τις ριζες για k = 8. Δεν μπορουμε απλα να το βαλουμε στην χαρακτηριστικη εξισωση και να λυσουμε? Σορρυ αν ειναι χαζομαρα αυτο που ρωταω!
+1Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: c0ndemn3d on January 31, 2014, 03:31:54 am
Να μην τέμνει ο ΓΤΡ το φανταστικό άξονα γιατί τότε πάνε οι ρίζες δεξιά και έχεις αστάθεια
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 31, 2014, 03:51:51 am
Στην ιδια ασκηση μπορει καποιος να μου εξηγησει τι ειναι αυτη η βοηθητικη εξισωση που γραφει οταν θελει να βρει τις ριζες για k = 8. Δεν μπορουμε απλα να το βαλουμε στην χαρακτηριστικη εξισωση και να λυσουμε? Σορρυ αν ειναι χαζομαρα αυτο που ρωταω!
+1H βοηθητική εξίσωση μπαίνει όταν στον Routh εμφανίζεται μηδενικό για να συνεχίσεις τον αλγόριθμο. Η βοηθητική βγαίνει με το ίδιο μοτίβο με το οποίο τοποθετείς αρχικά τους συντελεστές σου στο Routh (ενα ζιγκ-ζαγκ, πάνω-κάτω-πανω δεξιά-κάτω κοκ), ξεκινώντας με το στοιχείο της πρώτης στήλης πάνω από το μηδενικό και βάζοντας δίπλα σε κάθε συντελεστή την μεταβλητή s με βαθμό σύμφωνα με το μοτίβο. Δείτε και σελίδα 287 πετρίδη: Αν πάνω από το μηδενικό έχεις τον αριθμό 4 που αντιστοιχεί στη γραμμή s^4 από κάτω το μηδεν αντιστοιχεί στο s^3, συνεχίζουμε το μοτίβο: πάνω δεξιά 24 άρα αντιστοιχεί στο s^2 κάτω μηδέν στο s κοκ, οπότε βγαίνει:
4s^4 + 0s^3 + 24s^2 + 0s + 100, όπως στο βιβλίο.
Τώρα στην συγκεκριμένη άσκηση θεωρεί ότι το k παίρνει την οριακή τιμή για ευστάθεια (δηλαδή εκεί που το σύστημα πάει να γίνει ασταθές -> εκεί που οι πόλοι πάνε να περάσουν στο ΔΗΠ), οπότε αφού το k πήρε την οριακή τιμή το συγκεκριμένο κλάσμα στον πίνακα Routh γίνεται μηδέν οπότε έχουμε την πιο πάνω περίπτωση με την βοηθητική συνάρτηση, όπου και γι αυτό το k θα έχουμε δύο συζυγείς ρίζες πάνω στον φανταστικό (οριακή ευστάθεια). Εξισώνει την βοηθητική με το μηδέν και βρίσκει ποιες είναι αυτές οι ρίζες, οπότε και βρίσκει τα σημεία τομής του ΓΤΡ με τον φανταστικό άξονα.
Εάν το κατάλαβα καλά αυτό πρέπει να ναι. Τώρα γιατί εξισώνει την βοηθητική με το μηδέν και τι φυσική σημασία έχει η βοηθητική δεν έχω καταλάβει, γιατί λογικά πρέπει να ξέρεις πως βγήκε και ο αλγόριθμος του Routh. Αν ζητήσει σημεία τομής με Im-axis, τυφλοσούρτης και άγιος ο θεός.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 31, 2014, 10:08:42 am
Στην ιδια ασκηση μπορει καποιος να μου εξηγησει τι ειναι αυτη η βοηθητικη εξισωση που γραφει οταν θελει να βρει τις ριζες για k = 8. Δεν μπορουμε απλα να το βαλουμε στην χαρακτηριστικη εξισωση και να λυσουμε? Σορρυ αν ειναι χαζομαρα αυτο που ρωταω!
+1H βοηθητική εξίσωση μπαίνει όταν στον Routh εμφανίζεται μηδενικό για να συνεχίσεις τον αλγόριθμο. Η βοηθητική βγαίνει με το ίδιο μοτίβο με το οποίο τοποθετείς αρχικά τους συντελεστές σου στο Routh (ενα ζιγκ-ζαγκ, πάνω-κάτω-πανω δεξιά-κάτω κοκ), ξεκινώντας με το στοιχείο της πρώτης στήλης πάνω από το μηδενικό και βάζοντας δίπλα σε κάθε συντελεστή την μεταβλητή s με βαθμό σύμφωνα με το μοτίβο. Δείτε και σελίδα 287 πετρίδη: Αν πάνω από το μηδενικό έχεις τον αριθμό 4 που αντιστοιχεί στη γραμμή s^4 από κάτω το μηδεν αντιστοιχεί στο s^3, συνεχίζουμε το μοτίβο: πάνω δεξιά 24 άρα αντιστοιχεί στο s^2 κάτω μηδέν στο s κοκ, οπότε βγαίνει:
4s^4 + 0s^3 + 24s^2 + 0s + 100, όπως στο βιβλίο.
Τώρα στην συγκεκριμένη άσκηση θεωρεί ότι το k παίρνει την οριακή τιμή για ευστάθεια (δηλαδή εκεί που το σύστημα πάει να γίνει ασταθές -> εκεί που οι πόλοι πάνε να περάσουν στο ΔΗΠ), οπότε αφού το k πήρε την οριακή τιμή το συγκεκριμένο κλάσμα στον πίνακα Routh γίνεται μηδέν οπότε έχουμε την πιο πάνω περίπτωση με την βοηθητική συνάρτηση, όπου και γι αυτό το k θα έχουμε δύο συζυγείς ρίζες πάνω στον φανταστικό (οριακή ευστάθεια). Εξισώνει την βοηθητική με το μηδέν και βρίσκει ποιες είναι αυτές οι ρίζες, οπότε και βρίσκει τα σημεία τομής του ΓΤΡ με τον φανταστικό άξονα.
Εάν το κατάλαβα καλά αυτό πρέπει να ναι. Τώρα γιατί εξισώνει την βοηθητική με το μηδέν και τι φυσική σημασία έχει η βοηθητική δεν έχω καταλάβει, γιατί λογικά πρέπει να ξέρεις πως βγήκε και ο αλγόριθμος του Routh. Αν ζητήσει σημεία τομής με Im-axis, τυφλοσούρτης και άγιος ο θεός.
Για το γιατί παίρνει αυτό το βοηθητικό πολυώνυμο για να βρει τα σημεία τομής με τον φανταστικό άξονα:
Θέλεις να βρεις τα σημεία τομής του ΓΤΡ με τον φανταστικό άξονα. Άρα ξέρεις πως υπάρχει ένα ζεύγος s = +-jω για το οποίο η εξίσωση Κ * A(s) = -1 ικανοποιείται (αφού σύμφωνα με αυτήν σχεδιάζεις τον ΓΤΡ, ας σημειωθεί εδωπέρα πως με την ίδια εξίσωση γίνεται και το Routh). Επομένως, αν πάρεις την εξίσωση και βάλεις όπου s το jω και όπου Κ την οριακή τιμή για ευστάθεια, θα βγάλεις έναν μιγαδικό αριθμό ίσο με το μηδέν. Αν εξισώσεις το πραγματικό και το φανταστικό μέρος αυτού του μιγαδικού με το μηδέν, θα βγάλεις δύο εξισώσεις. Εσύ θέλεις μόνο τη μία από τις δύο (μιας και η μόνη σου μεταβλητή είναι το ω). Η μία εξίσωση θα είναι το πραγματικό μέρος να ισούται με το μηδέν (που θα έχει προκύψει από του όρους με άρτιες δυνάμεις, στους οποίους το μιγαδικό j έγινε πραγματικός αριθμός) και η άλλη θα είναι το φανταστικό μέρος να ισούται με το μηδέν (που θα έχει προκύψει από τους όρους με περιττές δυνάμεις, στους οποίους το μιγαδικό j βγήκε κοινός παράγοντας). Από την δεύτερη αυτή εξίσωση είναι που βγαίνει αυτό το βοηθητικό πολυώνυμο που βγάζουμε από τη δεύτερη σειρά του Routh. Θα μπορούσες να πάρεις, κάλλιστα, την πρώτη σειρά του Routh ως βοηθητικό πολύωνυμο για να βρεις το ζεύγος των φανταστικών λύσεων που είναι τα σημεία τομής με τον φανταστικό άξονα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: jason_ on January 31, 2014, 10:29:08 am
ωραίος Exomag, makes sense.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 31, 2014, 10:46:52 am
Στην ιδια ασκηση μπορει καποιος να μου εξηγησει τι ειναι αυτη η βοηθητικη εξισωση που γραφει οταν θελει να βρει τις ριζες για k = 8. Δεν μπορουμε απλα να το βαλουμε στην χαρακτηριστικη εξισωση και να λυσουμε? Σορρυ αν ειναι χαζομαρα αυτο που ρωταω!
+1H βοηθητική εξίσωση μπαίνει όταν στον Routh εμφανίζεται μηδενικό για να συνεχίσεις τον αλγόριθμο. Η βοηθητική βγαίνει με το ίδιο μοτίβο με το οποίο τοποθετείς αρχικά τους συντελεστές σου στο Routh (ενα ζιγκ-ζαγκ, πάνω-κάτω-πανω δεξιά-κάτω κοκ), ξεκινώντας με το στοιχείο της πρώτης στήλης πάνω από το μηδενικό και βάζοντας δίπλα σε κάθε συντελεστή την μεταβλητή s με βαθμό σύμφωνα με το μοτίβο. Δείτε και σελίδα 287 πετρίδη: Αν πάνω από το μηδενικό έχεις τον αριθμό 4 που αντιστοιχεί στη γραμμή s^4 από κάτω το μηδεν αντιστοιχεί στο s^3, συνεχίζουμε το μοτίβο: πάνω δεξιά 24 άρα αντιστοιχεί στο s^2 κάτω μηδέν στο s κοκ, οπότε βγαίνει:
4s^4 + 0s^3 + 24s^2 + 0s + 100, όπως στο βιβλίο.
Τώρα στην συγκεκριμένη άσκηση θεωρεί ότι το k παίρνει την οριακή τιμή για ευστάθεια (δηλαδή εκεί που το σύστημα πάει να γίνει ασταθές -> εκεί που οι πόλοι πάνε να περάσουν στο ΔΗΠ), οπότε αφού το k πήρε την οριακή τιμή το συγκεκριμένο κλάσμα στον πίνακα Routh γίνεται μηδέν οπότε έχουμε την πιο πάνω περίπτωση με την βοηθητική συνάρτηση, όπου και γι αυτό το k θα έχουμε δύο συζυγείς ρίζες πάνω στον φανταστικό (οριακή ευστάθεια). Εξισώνει την βοηθητική με το μηδέν και βρίσκει ποιες είναι αυτές οι ρίζες, οπότε και βρίσκει τα σημεία τομής του ΓΤΡ με τον φανταστικό άξονα.
Εάν το κατάλαβα καλά αυτό πρέπει να ναι. Τώρα γιατί εξισώνει την βοηθητική με το μηδέν και τι φυσική σημασία έχει η βοηθητική δεν έχω καταλάβει, γιατί λογικά πρέπει να ξέρεις πως βγήκε και ο αλγόριθμος του Routh. Αν ζητήσει σημεία τομής με Im-axis, τυφλοσούρτης και άγιος ο θεός.
Για το γιατί παίρνει αυτό το βοηθητικό πολυώνυμο για να βρει τα σημεία τομής με τον φανταστικό άξονα:
Θέλεις να βρεις τα σημεία τομής του ΓΤΡ με τον φανταστικό άξονα. Άρα ξέρεις πως υπάρχει ένα ζεύγος s = +-jω για το οποίο η εξίσωση Κ * A(s) = -1 ικανοποιείται (αφού σύμφωνα με αυτήν σχεδιάζεις τον ΓΤΡ, ας σημειωθεί εδωπέρα πως με την ίδια εξίσωση γίνεται και το Routh). Επομένως, αν πάρεις την εξίσωση και βάλεις όπου s το jω και όπου Κ την οριακή τιμή για ευστάθεια, θα βγάλεις έναν μιγαδικό αριθμό ίσο με το μηδέν. Αν εξισώσεις το πραγματικό και το φανταστικό μέρος αυτού του μιγαδικού με το μηδέν, θα βγάλεις δύο εξισώσεις. Εσύ θέλεις μόνο τη μία από τις δύο (μιας και η μόνη σου μεταβλητή είναι το ω). Η μία εξίσωση θα είναι το πραγματικό μέρος να ισούται με το μηδέν (που θα έχει προκύψει από του όρους με άρτιες δυνάμεις, στους οποίους το μιγαδικό j έγινε πραγματικός αριθμός) και η άλλη θα είναι το φανταστικό μέρος να ισούται με το μηδέν (που θα έχει προκύψει από τους όρους με περιττές δυνάμεις, στους οποίους το μιγαδικό j βγήκε κοινός παράγοντας). Από την δεύτερη αυτή εξίσωση είναι που βγαίνει αυτό το βοηθητικό πολυώνυμο που βγάζουμε από τη δεύτερη σειρά του Routh. Θα μπορούσες να πάρεις, κάλλιστα, την πρώτη σειρά του Routh ως βοηθητικό πολύωνυμο για να βρεις το ζεύγος των φανταστικών λύσεων που είναι τα σημεία τομής με τον φανταστικό άξονα.
Ευχαριστω παρα πολυ!! :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on January 31, 2014, 11:18:34 am
Τέλος να σημειώσω πως η πλήρως αναλυτική, και όχι και βέλτιστη για την εξεταστική, λύση είναι να πάρεις την εξίσωση K * A(s) = -1 και να αντικαταστήσεις το οριακό Κ που βρήκες από το Routh. Έπειτα θα λύσεις την εξίσωση (ως προς s), και έτσι θα βρεις τις θέσεις ΟΛΩΝ των πόλων για το δεδομένο Κ. Δύο από αυτούς τους πόλους, θα είναι σίγουρα το ζεύγος συζυγών φανταστικών πόλων που ψάχνεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Schro on January 31, 2014, 11:28:48 am
Τέλος να σημειώσω πως η πλήρως αναλυτική, και όχι και βέλτιστη για την εξεταστική, λύση είναι να πάρεις την εξίσωση K * A(s) = -1 και να αντικαταστήσεις το οριακό Κ που βρήκες από το Routh. Έπειτα θα λύσεις την εξίσωση (ως προς s), και έτσι θα βρεις τις θέσεις ΟΛΩΝ των πόλων για το δεδομένο Κ. Δύο από αυτούς τους πόλους, θα είναι σίγουρα το ζεύγος συζυγών φανταστικών πόλων που ψάχνεις.
Ναι ετσι το σκεφτηκα εγω, αλλα το αλλο ειναι οτι πρεπει για την εξεταση!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on June 17, 2014, 18:52:28 pm
Όταν ζητάει ΓΤΡ μπορώ να κάνω προσέγγιση κύριου πόλου ή πρέπει να το σχεδιάσω όπως είναι?(π.χ. θεμα 1 σεπτ 2013)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on June 17, 2014, 19:03:01 pm
Όταν ζητάει ΓΤΡ μπορώ να κάνω προσέγγιση κύριου πόλου ή πρέπει να το σχεδιάσω όπως είναι?(π.χ. θεμα 1 σεπτ 2013)
den exw thn ekfwnhsh mprosta moy alla mhn kaneis proseggish sto rlocus Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on June 17, 2014, 20:46:04 pm
στο θέμα 1 σεπτεμβρίου 2013,εκεί που ζητάει που θα βάλουμε το μηδενικό.Αν βλάλουμε το μηδενικό στο 5,θα μείνουν οι πόλοι 7 και 18,και από το χρόνο αποκατάστασης βγαίνει σ>8.32 αρα δεν ικανοποιείται αυτό που ζητάει.Τότε τι κάνουμε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on June 17, 2014, 21:05:46 pm
στο θέμα 1 σεπτεμβρίου 2013,εκεί που ζητάει που θα βάλουμε το μηδενικό.Αν βλάλουμε το μηδενικό στο 5,θα μείνουν οι πόλοι 7 και 18,και από το χρόνο αποκατάστασης βγαίνει σ>8.32 αρα δεν ικανοποιείται αυτό που ζητάει.Τότε τι κάνουμε?
Γιατι να το βάλεις στο 5?
θες οπως σωστά λες σ>8 δλδ
και βρίσκεις σημειο τομής ασυμπ. σα=(-30+μ)/2
Άτυπα τελειως μπορω να πω οτι θελω και οι ασυμπτωτες να ειναι αριστεροτερα του -8 ετσι ωστε να παρασύτω του πόλους
(-30+μ)/2< -8 => -30 + μ<-16 => μ<14
)
επομένως αν βάλω πχ το μηδενικό στο -10
ο πόλος στο -18 ----> -10
και οι αλλοι 2 πανε στην ασύμπτωτη στο 10
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on June 17, 2014, 21:07:45 pm
ευχαριστώ aggalitsas νασαι καλα
και ένα τελευταίο
και στο θέμα 2 σεπτ 2013,στο γ παίρνουμε 180+tan-1(ωc)-tan-1(ωc/4)-tan-1(ωc/20)>40 και μια σχέση από το |Α(jωc)|=1 και δοκιμάζουμε διάφορα μ ώστε να ισχύει η πρώτη σχέση?Σε μένα για διάφορα μ μου βγαίνει η συχνότητα γύρω στα 28 και αυτό δεν ικανοποιεί τη πρώτη σχέση
και ένα τελευταίο
και στο θέμα 2 σεπτ 2013,στο γ παίρνουμε 180+tan-1(ωc)-tan-1(ωc/4)-tan-1(ωc/20)>40 και μια σχέση από το |Α(jωc)|=1 και δοκιμάζουμε διάφορα μ ώστε να ισχύει η πρώτη σχέση?Σε μένα για διάφορα μ μου βγαίνει η συχνότητα γύρω στα 28 και αυτό δεν ικανοποιεί τη πρώτη σχέση
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on June 17, 2014, 21:14:39 pm
ευχαριστώ aggalitsas νασαι καλα
και ένα τελευταίο
και στο θέμα 2 σεπτ 2013,στο γ παίρνουμε 180+tan-1(ωc)-tan-1(ωc/4)-tan-1(ωc/20)>40 και μια σχέση από το |Α(jωc)|=1 και δοκιμάζουμε διάφορα μ ώστε να ισχύει η πρώτη σχέση?Σε μένα για διάφορα μ μου βγαίνει η συχνότητα γύρω στα 28 και αυτό δεν ικανοποιεί τη πρώτη σχέση
και ένα τελευταίο
και στο θέμα 2 σεπτ 2013,στο γ παίρνουμε 180+tan-1(ωc)-tan-1(ωc/4)-tan-1(ωc/20)>40 και μια σχέση από το |Α(jωc)|=1 και δοκιμάζουμε διάφορα μ ώστε να ισχύει η πρώτη σχέση?Σε μένα για διάφορα μ μου βγαίνει η συχνότητα γύρω στα 28 και αυτό δεν ικανοποιεί τη πρώτη σχέση
για το προηγούμενο ερώτημα
(http://i57.tinypic.com/j5lfeg.jpg)
για αυτό το ερώτημα θέλεις να βάλεις ενα μηδενικό να σου δώσει 90μοίρες για μεγάλα ω ετσι ώστε να κανεις counter το S toy παρανομαστή
επομένως θέλεις να σου δώσει αυτες τις 90 μοίρες φάσης όσο το δυαντό πιο γρήγορα
απο ρουθ βρίσκεις 0<μ<26
ετσι για μ=1
to PhaseMargin παει στις 41μοίρες
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on June 17, 2014, 21:19:41 pm
με έσωσες σ'ευχαριστώ!!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Atsi on June 17, 2014, 22:06:07 pm
Το εύρος ζώνης είναι η συχνότητα όπου το μέτρο Η(jω) πέφτει κατά 3 DB από το αρχικό ή το ω όπου μειώνεται το αρχικό κατά 30%;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on June 17, 2014, 22:37:41 pm
Το εύρος ζώνης είναι η συχνότητα όπου το μέτρο Η(jω) πέφτει κατά 3 DB από το αρχικό ή το ω όπου μειώνεται το αρχικό κατά 30%;;
Το πρώτο, με τα -3db, που γραφείς νομίζω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: yannis1092 on June 17, 2014, 23:42:10 pm
στο θέμα 1 σεπτεμβρίου 2013,εκεί που ζητάει που θα βάλουμε το μηδενικό.Αν βλάλουμε το μηδενικό στο 5,θα μείνουν οι πόλοι 7 και 18,και από το χρόνο αποκατάστασης βγαίνει σ>8.32 αρα δεν ικανοποιείται αυτό που ζητάει.Τότε τι κάνουμε?
Γιατι να το βάλεις στο 5?
θες οπως σωστά λες σ>8 δλδ
και βρίσκεις σημειο τομής ασυμπ. σα=(-30+μ)/2
Άτυπα τελειως μπορω να πω οτι θελω και οι ασυμπτωτες να ειναι αριστεροτερα του -8 ετσι ωστε να παρασύτω του πόλους
(-30+μ)/2< -8 => -30 + μ<-16 => μ<14
)
επομένως αν βάλω πχ το μηδενικό στο -10
ο πόλος στο -18 ----> -10
και οι αλλοι 2 πανε στην ασύμπτωτη στο 10
Αν θεωρηθεί σωστή η λογική ότι προσθέτω μηδενικό για να απαλοιφθεί ένας αργός πόλος τότε μπορώ να βάλω μ=5. Από ΓΤΡ το ΟΑ = -12.5 και ο ένας πόλος πάει στο +inf και ο άλλος στο -inf. Συνεπώς, για μεγάλα Κ, οι πόλοι θα έχουν -σ < -8.32
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on June 18, 2014, 07:15:01 am
στο θέμα 1 σεπτεμβρίου 2013,εκεί που ζητάει που θα βάλουμε το μηδενικό.Αν βλάλουμε το μηδενικό στο 5,θα μείνουν οι πόλοι 7 και 18,και από το χρόνο αποκατάστασης βγαίνει σ>8.32 αρα δεν ικανοποιείται αυτό που ζητάει.Τότε τι κάνουμε?
Γιατι να το βάλεις στο 5?
θες οπως σωστά λες σ>8 δλδ
και βρίσκεις σημειο τομής ασυμπ. σα=(-30+μ)/2
Άτυπα τελειως μπορω να πω οτι θελω και οι ασυμπτωτες να ειναι αριστεροτερα του -8 ετσι ωστε να παρασύτω του πόλους
(-30+μ)/2< -8 => -30 + μ<-16 => μ<14
)
επομένως αν βάλω πχ το μηδενικό στο -10
ο πόλος στο -18 ----> -10
και οι αλλοι 2 πανε στην ασύμπτωτη στο 10
Αν θεωρηθεί σωστή η λογική ότι προσθέτω μηδενικό για να απαλοιφθεί ένας αργός πόλος τότε μπορώ να βάλω μ=5. Από ΓΤΡ το ΟΑ = -12.5 και ο ένας πόλος πάει στο +inf και ο άλλος στο -inf. Συνεπώς, για μεγάλα Κ, οι πόλοι θα έχουν -σ < -8.32
Γενικα νομίζω δεν απαλείφουμε για να μην αλλάξεις την μορφής της ελεγχόμενης διεργασίας.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Rising Force on June 18, 2014, 14:05:24 pm
έλυσε κάποιος το θέμα με τον ασταθή πόλο;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on June 18, 2014, 14:26:51 pm
έλυσε κάποιος το θέμα με τον ασταθή πόλο;;
Αυτό που έκανα εγώ είναι να βάλω αρχικά ελεγκτή K(s+z), και έπειτα ελεγκτή K(s+z)/s.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Chester on June 18, 2014, 15:40:24 pm
Δεν μπορούσαμε να βάλουμε Κ(s-7) αρχικά για να διώξουμε αυτό το (s-7) ?
Έπειτα να προσθέσουμε το 1/s.
Έπειτα να προσθέσουμε το 1/s.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: aggalitsas on June 18, 2014, 16:32:59 pm
έλυσε κάποιος το θέμα με τον ασταθή πόλο;;
το έλυσα, και επιβεβαίωσα τη λύση με το κ. Θεοχάρη.Αρχικά εχεις την ασύμπτωτη στο Δεξι μιγαδικό επίπεδο κανεις το -7 μεταβλητή και βρίσκειες νεο AO<0
μετα θέλεις PD controller Κ(s+c)
και μετα PID K(s+c1)(s+c2)/s (@exomag αν βάλεις PI δεν έχεις ευστάθεια)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on June 18, 2014, 16:39:59 pm
έλυσε κάποιος το θέμα με τον ασταθή πόλο;;
το έλυσα, και επιβεβαίωσα τη λύση με το κ. Θεοχάρη.Αρχικά εχεις την ασύμπτωτη στο Δεξι μιγαδικό επίπεδο κανεις το -7 μεταβλητή και βρίσκειες νεο AO<0
μετα θέλεις PD controller Κ(s+c)
και μετα PID K(s+c1)(s+c2)/s (@exomag αν βάλεις PI δεν έχεις ευστάθεια)
Το δεύτερο πάντως λυνόταν και με σκέτο PI νομίζω, δεν είναι ανάγκη να βάλεις PID.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Chester on June 18, 2014, 17:25:14 pm
Παιδιά, παίζει να είναι σωστό να βάλουμε στον ελεγκτή μηδενικό για να φύγει ο θετικός πόλος s=+7 ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on June 18, 2014, 17:34:45 pm
Παιδιά, παίζει να είναι σωστό να βάλουμε στον ελεγκτή μηδενικό για να φύγει ο θετικός πόλος s=+7 ?
Θεωρητικά σωστό είναι, τώρα το τι θα δεχτεί ο Θεοχάρης σαν σωστό είναι άλλο ζήτημα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Nerevar on June 18, 2014, 18:15:20 pm
Παιδιά, παίζει να είναι σωστό να βάλουμε στον ελεγκτή μηδενικό για να φύγει ο θετικός πόλος s=+7 ?
Θεωρητικά σωστό είναι, τώρα το τι θα δεχτεί ο Θεοχάρης σαν σωστό είναι άλλο ζήτημα.
Μάλλον όχι,το ότι έχεις ΣΚΒ με απλοποιημένο ασταθή πόλο δε σημαίνει ότι και οι υπόλοιπες συναρτήσεις μεταφοράς (διαταραχών/θορύβου/κτλ) θα είναι επίσης ευσταθείς,εκτός της ακραίας περίπτωσης όπου σου λέει ότι δεν υπάρχουν οι τελευταίες.Το ανέφερει και ο πετρίδης κάπου στο δεύτερο τόμο του με bold,θα ψάξω να το βρω.
YΓ:Σελίδα 208.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on June 18, 2014, 18:32:06 pm
Παιδιά, παίζει να είναι σωστό να βάλουμε στον ελεγκτή μηδενικό για να φύγει ο θετικός πόλος s=+7 ?
Θεωρητικά σωστό είναι, τώρα το τι θα δεχτεί ο Θεοχάρης σαν σωστό είναι άλλο ζήτημα.
Μάλλον όχι,το ότι έχεις ΣΚΒ με απλοποιημένο ασταθή πόλο δε σημαίνει ότι και οι υπόλοιπες συναρτήσεις μεταφοράς (διαταραχών/θορύβου/κτλ) θα είναι επίσης ευσταθείς,εκτός της ακραίας περίπτωσης όπου σου λέει ότι δεν υπάρχουν οι τελευταίες.Το ανέφερει και ο πετρίδης κάπου στο δεύτερο τόμο του με bold,θα ψάξω να το βρω.
Δεκτό, απλά εσύ το πας προς το μη-θεωρητικό κομμάτι και εμείς δεν έχουμε αναφέρει γενικά κάτι τέτοιο απ' όσο ξέρω. Και πάλι, βέβαια, με επιφύλαξη αυτά που λέω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Chester on June 18, 2014, 19:11:49 pm
Δηλαδή θα πρέπει να έχω διαβάσει 2 τόμους του Πετρίδη ώστε να είμαι καλυμμένος για κάθε περίπτωση και θέμα που μπορεί να βάλει ο άλλος ??
Γιατί δεν εξετάζουν αυτά που διδάσκουν; Έστω να αφιερώσουν κάποιες ασκήσεις από την αίθουσα σε τέτοια ζητήματα.
Τέλος πάντων, λογικά καλό Σεπτέμβρη πάλι.
Γιατί δεν εξετάζουν αυτά που διδάσκουν; Έστω να αφιερώσουν κάποιες ασκήσεις από την αίθουσα σε τέτοια ζητήματα.
Τέλος πάντων, λογικά καλό Σεπτέμβρη πάλι.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Nerevar on June 18, 2014, 19:20:34 pm
Δηλαδή θα πρέπει να έχω διαβάσει 2 τόμους του Πετρίδη ώστε να είμαι καλυμμένος για κάθε περίπτωση και θέμα που μπορεί να βάλει ο άλλος ??
Φυσικά και όχι,αλλά δεν μπορεί κανείς να πει ότι είναι γνώση των σαε2 το συγκεκριμένο κομμάτι,από τη στιγμή που υπολογίζοντας την Hyd/Hyn/κτλ θα έβλεπες ότι ο ασταθής πόλος παραμένει.Στο θέμα βέβαια που σας έβαλε δε δίνει διαταραχές/θόρυβο (ο πετρίδης έλεγε ότι τα d/n εισάγονται πάντα στο ίδιο σημείο του βρόχου,αρα δεν υπάρχει αβεβαιότητα ως προς αυτό το κομμάτι),οπότε καλύτερα να ρωτήσεις κάποιον από αυτούς που έβαλαν τα θέματα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: yannis1092 on June 18, 2014, 20:48:04 pm
Σε ερώτηση που έκανα στο Θεοχάρη (γιατί κι εγώ με απαλοιφή του ασταθούς πόλου το πήγα) απάντησε ότι δεν είναι ορθή λογική αυτή. Τώρα το πως ακριβώς θα βαθμολογήσει είναι άλλο θέμα... Πάντως, για να είμαστε σωστοί, απαλοιφή ασταθών πόλων ΔΕΝ πρέπει να κάνουμε και αναφέρεται και στον 1ο τόμο σελ. 376
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: copernicus on August 29, 2014, 12:48:04 pm
Στο θέμα 3 Σεπτ 2010,λογικά παίρνουμε αναλογικό ελεγκτή,όμως με τον αναλογικό ελεγκτή δεν μπορώ να επηρεάσω τον χρόνο αποκατάστασης.Για το πρώτο κριτήριο που ζητάει ελάχιστο χρόνο αποκατάστασης τι κάνω?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pentium4 on August 31, 2014, 01:16:37 am
γενικά και για εδώ και για άλλα τόπικ, για λιγότερη ταλαιπωρία αλλά και για να μένουν (γιατί από dropbox κτλ συνήθως τα "πετάτε")
στα τόπικ με λυμένα θέματα για απορίες και λύσεις,στην 1η σειρά το θέμα (πχ Σεπτέμβρης 2012) με bold και τα λυμένα
που ανεβάζετε ως συνημμένα (όπως μπήκαν δηλαδή πιο πάνω) και όχι dropbox κτλ (αν θέλετε τα κατεβάζετε,αν είναι λάθος κτλ).γενικά αυτά,απλά το θυμήθηκα
στα τόπικ με λυμένα θέματα για απορίες και λύσεις,στην 1η σειρά το θέμα (πχ Σεπτέμβρης 2012) με bold και τα λυμένα
που ανεβάζετε ως συνημμένα (όπως μπήκαν δηλαδή πιο πάνω) και όχι dropbox κτλ (αν θέλετε τα κατεβάζετε,αν είναι λάθος κτλ).γενικά αυτά,απλά το θυμήθηκα
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ALEO on August 31, 2014, 21:47:16 pm
Ιανουάριος 2013 θέμα 2. Επιλέγουμε τον ελεγκτή Hc2 και γιατι ?? Τον χρόνο αποκατάστασης πως τον χρησιμοποιούμε??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: konsntev on August 31, 2014, 23:16:44 pm
Λοιπόν παιδιά σε πολλά παλιά θέματα δίνει ts... Τι κάνουμε τότε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasl12 on September 01, 2014, 12:48:29 pm
Λοιπόν παιδιά σε πολλά παλιά θέματα δίνει ts... Τι κάνουμε τότε?
παιρνεις τον τυπο σελ 388 πετριδη με το σ και μετα παίρνεις τους περιορισμους που σε βολευουν για το πραγματικο μερος των πολων
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ευχαριστο Διαλειμμα on September 01, 2014, 18:54:17 pm
Επειδή άκουσα αρκετούς να κάνουν βασικό λάθος με το εύρος ζώνης θα το γράψω να το ξεκαθαρίσω.
Το εύρος ζώνης είναι μέχρι τη συχνότητα στην οποία το πλάτος της αρχικής τιμής του μέτρου |H(jω)| πέφτει στο 0.707 της αρχικής τιμής |H(0)|, δηλαδή στο 0.707*|Η(0)|. Με απλές πράξεις λογαρίθμων καταλήγουμε στο:
(Επειδή το tex τον πίνει σε εικόνα)
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=8325.0;attach=50901)
Άρα το εύρος ζώνης βρίσκεται πάντα στο σημείο του διαγράμματος Bode πλάτους που πέφτει το μέτρο του πλάτους κατά 3(db) σε σχέση με την αρχική τιμή ΚΑΙ ΟΧΙ ΣΤΟ 0.707*20log|H(0)| που άκουσα αρκετούς να λένε.
Το εύρος ζώνης είναι μέχρι τη συχνότητα στην οποία το πλάτος της αρχικής τιμής του μέτρου |H(jω)| πέφτει στο 0.707 της αρχικής τιμής |H(0)|, δηλαδή στο 0.707*|Η(0)|. Με απλές πράξεις λογαρίθμων καταλήγουμε στο:
(Επειδή το tex τον πίνει σε εικόνα)
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=8325.0;attach=50901)
Άρα το εύρος ζώνης βρίσκεται πάντα στο σημείο του διαγράμματος Bode πλάτους που πέφτει το μέτρο του πλάτους κατά 3(db) σε σχέση με την αρχική τιμή ΚΑΙ ΟΧΙ ΣΤΟ 0.707*20log|H(0)| που άκουσα αρκετούς να λένε.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ΚΗΜΜΥ on September 01, 2014, 18:55:18 pm
Ενταξει, μη συγχυζεσαι :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ευχαριστο Διαλειμμα on September 01, 2014, 19:06:55 pm
Ενταξει, μη συγχυζεσαι :P
Για μένα κλάιν, πέρασα, δε με απασχολεί, για εκείνους το γράφω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SportBillyPap on February 02, 2015, 00:12:33 am
να ρωτησω κατι.οταν μας λεει χρονο αποκαταστασης <0.5 πχ και λεμε σ>8 συνηθως ενα κλαδο ο οποιος ειναι δεξια του πχ απο -2 εως -1 εμας μας ενδιαφερει το ΟΑ να ειναι <-8 ?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 01:33:05 am
να ρωτησω κατι.οταν μας λεει χρονο αποκαταστασης <0.5 πχ και λεμε σ>8 συνηθως ενα κλαδο ο οποιος ειναι δεξια του πχ απο -2 εως -1 εμας μας ενδιαφερει το ΟΑ να ειναι <-8 ?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
ΟΑ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Αλντεμπαράν on February 02, 2015, 01:36:59 am
Λογικά αναφέρεται στο σημείο τομής των ασυμπτώτων.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 01:39:39 am
να ρωτησω κατι.οταν μας λεει χρονο αποκαταστασης <0.5 πχ και λεμε σ>8 συνηθως ενα κλαδο ο οποιος ειναι δεξια του πχ απο -2 εως -1 εμας μας ενδιαφερει το ΟΑ να ειναι <-8 ?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
Δηλαδη εννοω μας λεει ts<0.5 αρα σ>8 Αρα για το συστημα kp/((s+6)(s-7) διαλεγουμε μηδενικο στο 9 αρα επι (s+9) αρα το ΟΑ=-8 αρα αυτο μας νοιαζει?
Δεν ισχύει αυτό που λες. Το ΟΑ είναι απλά το σημείο τομής των ασυμπτώτων των κλάδων των πόλων το ΣΚΒ. Άμα θες σ>8, θες (για κάποιο συγκεκριμένο κέρδος) όλοι οι πόλοι του ΣΚΒ να έχουν πραγματικό μέρος μεγαλύτερο κατά απόλυτη τιμή από 8.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SportBillyPap on February 02, 2015, 01:41:32 am
βασικα νομιζω καταλαβα νομιζω οτι δε μπορουμε να παρουμε για ολα τα Κ τον περιορισμο πx ts<0.5 αρα επιλεγουμε για μεγαλα Κ να οδησουμαστε σε μηδενικα που εχουν σ>8 η στο απειρο για αυτο επιλεγουμε το μηδενικο στο 9 ..κανω λαθος?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 01:42:59 am
βασικα νομιζω καταλαβα νομιζω οτι δε μπορουμε να παρουμε για ολα τα Κ τον περιορισμο πx ts<0.5 αρα επιλεγουμε για μεγαλα Κ να οδησουμαστε σε μηδενικα που εχουν σ>8 η στο απειρο για αυτο επιλεγουμε το μηδενικο στο 9 ..κανω λαθος?
Προφανώς θες ΟΑ κατά απόλυτη τιμή μεγαλύτερο από 8. Άρα το μηδενικό στο 9 δε σου κάνει ακριβώς τη δουλεία, θες μηδενικό > 9.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SportBillyPap on February 02, 2015, 01:47:00 am
Αρα εν τελει οταν μας λεει ts<a εμεις παιρνουμε εναν ελεκτη του τυπου Κ(s+c) αρα θελουμε ΟΑ=(..)/n-m <-4/a αρα λεμε c=.. Σωστα?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 01:54:15 am
Αρα εν τελει οταν μας λεει ts<a εμεις παιρνουμε εναν ελεκτη του τυπου Κ(s+c) αρα θελουμε ΟΑ=(..)/n-m <-4/a αρα λεμε c=.. Σωστα?
Ναι, και θα πρέπει ΟΑ > κατά απόλυτη τιμή από την προδιαγραφή για το σ (που θα βγεί απο το ts<a).
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SportBillyPap on February 02, 2015, 01:58:00 am
οκ ευχαριστω πολυ καταλαβα (ελπιζω να μην ηταν πολυ ηλιθια η απορια μου :P)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 12:33:56 pm
Θεμα σεπ.2013 το 1 το περιθωριο κερδους πως το βρισκω ;εβγαλα απο το routh 0<k<3450 αλλα στο βιβλιο γραφει Gm=ko/k πως λύνεται τελικα; :(
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 12:45:24 pm
Θεμα σεπ.2013 το 1 το περιθωριο κερδους πως το βρισκω ;εβγαλα απο το routh 0<k<3450 αλλα στο βιβλιο γραφει Gm=ko/k πως λύνεται τελικα; :(
Έχω και εγώ απορία για το περιθώριο κέρδους, αλλά στα θέματα του σεπτέμβρη 2014. Στο ΓΤ από routh βγάζω ότι έχω οριακή ευστάθεια για κ=0 ή κ=1/3 ( δηλαδή ισχύει 0<κ<1/3 ?), Και το περιθώριο κέρδους πιο είναι?Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 12:54:41 pm
Μπορει να το λυσει καποιος και να το ανεβάσει μηπως;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Avraam on February 02, 2015, 12:58:19 pm
Θεμα σεπ.2013 το 1 το περιθωριο κερδους πως το βρισκω ;εβγαλα απο το routh 0<k<3450 αλλα στο βιβλιο γραφει Gm=ko/k πως λύνεται τελικα; :(
Έχω και εγώ απορία για το περιθώριο κέρδους, αλλά στα θέματα του σεπτέμβρη 2014. Στο ΓΤ από routh βγάζω ότι έχω οριακή ευστάθεια για κ=0 ή κ=1/3 ( δηλαδή ισχύει 0<κ<1/3 ?), Και το περιθώριο κέρδους πιο είναι?Το κερδος που βρισκεις απο το Routh και στις 2 περιπτωσεις ειναι το μεγιστο κ που μπορεις να βαλεις στην συναρτηση ανοιχτου βροχου και να ειναι ευσταθης. Οποτε στο θεμα του Σεπ 2013 το περιθωριο κερδους σου ειναι το gm=3450/k και στην περιπτωση του σεπτεμβρη του 2014 ειναι gm=(1/3)/k γιατι ετσι κι αλλιως το κερδος σου θες να ειναι θετικο
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 13:06:10 pm
στη περιπτωση μετα που προσθετουμε μηδενικο εχουμε απειρο περιθωριο κερδους ετσι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 13:16:46 pm
Θεμα σεπ.2013 το 1 το περιθωριο κερδους πως το βρισκω ;εβγαλα απο το routh 0<k<3450 αλλα στο βιβλιο γραφει Gm=ko/k πως λύνεται τελικα; :(
Έχω και εγώ απορία για το περιθώριο κέρδους, αλλά στα θέματα του σεπτέμβρη 2014. Στο ΓΤ από routh βγάζω ότι έχω οριακή ευστάθεια για κ=0 ή κ=1/3 ( δηλαδή ισχύει 0<κ<1/3 ?), Και το περιθώριο κέρδους πιο είναι?Το κερδος που βρισκεις απο το Routh και στις 2 περιπτωσεις ειναι το μεγιστο κ που μπορεις να βαλεις στην συναρτηση ανοιχτου βροχου και να ειναι ευσταθης. Οποτε στο θεμα του Σεπ 2013 το περιθωριο κερδους σου ειναι το gm=3450/k και στην περιπτωση του σεπτεμβρη του 2014 ειναι gm=(1/3)/k γιατι ετσι κι αλλιως το κερδος σου θες να ειναι θετικο
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Avraam on February 02, 2015, 13:17:53 pm
στη περιπτωση μετα που προσθετουμε μηδενικο εχουμε απειρο περιθωριο κερδους ετσι;
Σωστος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: heavy melon on February 02, 2015, 13:21:40 pm
εκφωνήσεις από ιούνη 2013 παίζουν?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 14:57:16 pm
Παιδια θεμα 2 σεπ.2013 αν επιλεξω πρωτα το μηδενικο τυχαια και μετα επαληθευσω οτι ισχυει φμ.40 ισχυει ετσι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Αλντεμπαράν on February 02, 2015, 15:10:15 pm
Αρα εν τελει οταν μας λεει ts<a εμεις παιρνουμε εναν ελεκτη του τυπου Κ(s+c) αρα θελουμε ΟΑ=(..)/n-m <-4/a αρα λεμε c=.. Σωστα?
Ναι, και θα πρέπει ΟΑ > κατά απόλυτη τιμή από την προδιαγραφή για το σ (που θα βγεί απο το ts<a).
Διαφωνώ με την λύση που επισυνάπτω στο εξής:
(β ερώτημα)
Λέει Kp/Kd=9 γιατί |σ|>8, όμως αυτό είναι λάθος γιατί το σ αναφέρεται στο πραγματικό μέρος των πόλων και όχι των μηδενικών, και ο ελεγκτής εισάγει μηδενικό και όχι πόλο.
Βασιζόμενος,αν κατάλαβα, σε αυτό που λες λύνω ως εξής: ΟΑ>|σ|, για σ<-8 έχουμε ΟΑ<-8. Άρα 1/2(-6+7-Κp/Kd)<-8 => C>15.
Πώς σου φαίνεται;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 15:52:54 pm
Αρα εν τελει οταν μας λεει ts<a εμεις παιρνουμε εναν ελεκτη του τυπου Κ(s+c) αρα θελουμε ΟΑ=(..)/n-m <-4/a αρα λεμε c=.. Σωστα?
Ναι, και θα πρέπει ΟΑ > κατά απόλυτη τιμή από την προδιαγραφή για το σ (που θα βγεί απο το ts<a).
Διαφωνώ με την λύση που επισυνάπτω στο εξής:
(β ερώτημα)
Λέει Kp/Kd=9 γιατί |σ|>8, όμως αυτό είναι λάθος γιατί το σ αναφέρεται στο πραγματικό μέρος των πόλων και όχι των μηδενικών, και ο ελεγκτής εισάγει μηδενικό και όχι πόλο.
Βασιζόμενος,αν κατάλαβα, σε αυτό που λες λύνω ως εξής: ΟΑ>|σ|, για σ<-8 έχουμε ΟΑ<-8. Άρα 1/2(-6+7-Κp/Kd)<-8 => C>15.
Πώς σου φαίνεται;
Καταρχάς, να ξεκαθαριστεί πως τα μηδενικά είναι εκεί που θα καταλήξουν ο πόλοι του ΣΚΒ για μεγάλο κέρδος. Οπότε, από εκεί και πέρα, εξαρτάται πόσους πόλους/μηδενικά έχεις και άρα τι είδους ασύμπτωτες έχεις.
Αν έχεις διαφορά πόλων/μηδενικών 2, και άρα έχεις ασύμπτωτες κάθετες στον πραγματικό άξονα, τότε όντως πρέπει το ΟΑ < -8 (οπότε το μηδενικό θα βγεί αρκετά πιο αριστερά από το -8, λύνοντας από τον τύπο του ΟΑ).
Αν έχεις διαφορά πόλων/μηδενικών 1, και άρα έχεις ασύμπτωτη τον αρνητικό πραγματικό ημιάξονα, τότε πρέπει απλά το άλλο μηδενικό να είναι < -8. Αυτό διότι ο ένας πόλος θα πάει στο -inf και ο άλλος θα πάει στο μηδενικό. Οπότε πρέπει να φροντίσεις να έχει και το μηδενικό πραγματικό μέρος μικρότερο του -8. Σε αυτήν την περίπτωση ο τύπος του ΟΑ δε σου χρειάζεται.
Στο θέμα που με ρώτησες, στο (β) ερώτημα, πρόκειται για την περίπτωση αυτή. Γι' αυτόν τον λόγο απλά διαλέγει το μηδενικό να είναι < -8, και λέει Kp/Kd = 9.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mumm-ra ο παντοντινός on February 02, 2015, 16:12:55 pm
Πάντως Exomag στις σημειώσεις σου (σελ 21) ο Σταμούλης έχει έναν εναλλακτικό τρόπο να υπολογίζεις περιθώριο κέρδους,όταν τοποθετούμε ένα κέρδος Κ στον ευθύ κλάδο.Λέει ότι είναι απλά 20logK...
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: sk0uf on February 02, 2015, 16:30:29 pm
Πάντως Exomag στις σημειώσεις σου (σελ 21) ο Σταμούλης έχει έναν εναλλακτικό τρόπο να υπολογίζεις περιθώριο κέρδους,όταν τοποθετούμε ένα κέρδος Κ στον ευθύ κλάδο.Λέει ότι είναι απλά 20logK...
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Λογικά όχι.Θα βάλεις ένα ακόμα Κ και θα κάνεις ROuth και για εκείνο το Κ θα είναι 20logK.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 02, 2015, 17:52:06 pm
Αν μας βγει από το Routh ότι είμαστε ευσταθείς για κ>5 και ασταθείς για 0<κ<5, ποιο είναι τότε το περιθώριο κέρδους;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 17:55:57 pm
αποσβεση θορυβου καλυτερη απο -10 db τι εννοει;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 17:56:47 pm
Πάντως Exomag στις σημειώσεις σου (σελ 21) ο Σταμούλης έχει έναν εναλλακτικό τρόπο να υπολογίζεις περιθώριο κέρδους,όταν τοποθετούμε ένα κέρδος Κ στον ευθύ κλάδο.Λέει ότι είναι απλά 20logK...
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Επομένως,όπως πχ στον Σεπτ 2012,που έχω μια Hp και έναν αναλογικό ελεγκτή Κ,εφόσον μου λέει για Κ=2 βρες περιθώριο κέρδους,δεν γράφω απλά 20log2...? 8))
Λογικά όχι.Θα βάλεις ένα ακόμα Κ και θα κάνεις ROuth και για εκείνο το Κ θα είναι 20logK.
Και εγώ αυτό νομίζω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 17:58:20 pm
Αν μας βγει από το Routh ότι είμαστε ευσταθείς για κ>5 και ασταθείς για 0<κ<5, ποιο είναι τότε το περιθώριο κέρδους;;
Εφόσον το ΣΚΒ είναι ευσταθές από την αρχή (δεν έχει πόλους στο δεξί ημι-επίπεδο), τότε κάτι έκανες λάθος. Ο περιορισμός θα πρέπει να είναι της μορφής K < X.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 02, 2015, 18:03:37 pm
αποσβεση θορυβου καλυτερη απο -10 db τι εννοει;
(http://latex.codecogs.com/gif.download?%5Cdpi%7B120%7D%2020log%7CH_%7Byn%7D%7C%3C-10)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 18:38:51 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mumm-ra ο παντοντινός on February 02, 2015, 18:46:26 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 18:47:54 pm
οκ thanks !Μαλλον στις πραξεις θα εχω λαθος.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 02, 2015, 19:05:12 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 19:29:04 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 02, 2015, 20:15:31 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 20:24:25 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mumm-ra ο παντοντινός on February 02, 2015, 20:26:44 pm
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Γενικά ναι,ο Ναπολέων έκανε άλλο όμως. Ωραίος!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 02, 2015, 20:31:07 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Εκεί που γράφω παρατηρώ... Ξέχασα να βάλω το 20log εχεις δίκιο ,αλλά απο κάτω που το υπολογιζω το χω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 20:37:05 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Εκεί που γράφω παρατηρώ... Ξέχασα να βάλω το 20log εχεις δίκιο ,αλλά απο κάτω που το υπολογιζω το χω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: nlogn on February 02, 2015, 20:38:32 pm
Έχετε καμιά ιδέα για το πως να κάνω στο θέμα 2 του Γενάρη 11, το σ > 4 . Σίγουρα με ΓΤΡ, αλλά έχω δοκιμάσει τα πάντα και αυτός ο πόλος στο 0 που χρειάζεται, με το μηδενικό στο 2 απλά είναι "σκέτος πονοκέφαλος".
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 02, 2015, 20:45:12 pm
To θέμα ε΄΄ιναι λάθος Johny
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: SportBillyPap on February 02, 2015, 21:17:01 pm
To θέμα ε΄΄ιναι λάθος Johny
+1 στον ερωτιαρηTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mvp Morgul on February 02, 2015, 21:18:36 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Εκεί που γράφω παρατηρώ... Ξέχασα να βάλω το 20log εχεις δίκιο ,αλλά απο κάτω που το υπολογιζω το χω.
Γιατί να είναι έτσι; αφού το εύρος ζώνης είναι εκεί που η τιμή η αρχική έχει πέσει στο 70,7% και όχι απαραίτητα 3. δηλαδή θα έπρεπε να είναι 0.707* 20 db
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 02, 2015, 21:44:39 pm
Αν εχω ενα 2 μπροστα στην h(s) δεν αλλαζει κατι στο Γ.Τ.Ρ ετσι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 21:46:23 pm
Sep 2012 στο θεμα 1 το ωb ποσο βγαινει;; χρησιμοποιησα τον τυπο για την H(s) αλλα μου βγαινει πολυ ακυρο νουμερο για ζ=1,25 και ωn=10...Χρειαζεται κατι αλλο μηπως;
Θέλεις τέτοιο ωb,ώστε 20log|Η(jωb)| =20-3=17db
Οι πράξεις ειναι πραγματικά γάμησε τα,σόρρυ. ^aytoxeir^
Εαν δεν πάρεις την κανονική,αλλά την προσέγγιση που κάνουμε για το bode,οι πράξεις είναι πιο εύκολες
Γράψε μας την προσέγγιση που κάνεις
Δεν πρέπει να πεις 20log(H(wb))=17 και από εκεί να λύσεις? εννοώ όχι από Η(wb)=17 , αφού το 17 είναι Db και για να βγάλεις το H(wb) σε Db πρέπει να λογαριθμήσεις? Σορρυ αν σκαλώνω κάπου είμαι θολωμένος
Εκεί που γράφω παρατηρώ... Ξέχασα να βάλω το 20log εχεις δίκιο ,αλλά απο κάτω που το υπολογιζω το χω.
Γιατί να είναι έτσι; αφού το εύρος ζώνης είναι εκεί που η τιμή η αρχική έχει πέσει στο 70,7% και όχι απαραίτητα 3. δηλαδή θα έπρεπε να είναι 0.707* 20 db
H κλίμακα των αξόνων είναι λογαριθμισμένη. η μείωση στο 0.707 της αρχικής τιμής είναι πάντα 3 db (20log0.0702=-3.011 db ). Μπορείς αν θες να πεις ότι θα είναι εκεί που ισχύει Η(0)*0.707 αλλά για να το βάλεις στον άξονα πρέπει να το κάνεις επί 20log. Δηλαδή 20log(H(0)*0.707)= 20log(H(0)+20log0.707= Αρχική τιμή - 3 db
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Mvp Morgul on February 02, 2015, 22:13:34 pm
[
H κλίμακα των αξόνων είναι λογαριθμισμένη. η μείωση στο 0.707 της αρχικής τιμής είναι πάντα 3 db (20log0.0702=-3.011 db ). Μπορείς αν θες να πεις ότι θα είναι εκεί που ισχύει Η(0)*0.707 αλλά για να το βάλεις στον άξονα πρέπει να το κάνεις επί 20log. Δηλαδή 20log(H(0)*0.707)= 20log(H(0)+20log0.707= Αρχική τιμή - 3 db
H κλίμακα των αξόνων είναι λογαριθμισμένη. η μείωση στο 0.707 της αρχικής τιμής είναι πάντα 3 db (20log0.0702=-3.011 db ). Μπορείς αν θες να πεις ότι θα είναι εκεί που ισχύει Η(0)*0.707 αλλά για να το βάλεις στον άξονα πρέπει να το κάνεις επί 20log. Δηλαδή 20log(H(0)*0.707)= 20log(H(0)+20log0.707= Αρχική τιμή - 3 db
ευχαριστώ !
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 23:01:12 pm
Όποιος έχει λύσει θέμα 2ο σεπτέμβριο 2013 ας που πει πως στο καλό θα βγάλω την wc που ζητάει
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Avraam on February 02, 2015, 23:10:29 pm
Όποιος έχει λύσει θέμα 2ο σεπτέμβριο 2013 ας που πει πως στο καλό θα βγάλω την wc που ζητάει
Κοιτα εγω το εβγαλα απο το Bode και μου βγηκε 7.07 περιπου.. Σε προηγουμενα ποστ βεβαια το βγαζουν 6.53... Αυτο οφειλεται στο οτι εγω το πηρα απο το Bode ενω εκει πηραν τον τυπο |A(jωc)|, μονο που δεν ελαβαν τον πολο στο -20.. Τωρα αν θες αναλυτικες πραξεις με το Bode τις εχω..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 23:13:00 pm
Όποιος έχει λύσει θέμα 2ο σεπτέμβριο 2013 ας που πει πως στο καλό θα βγάλω την wc που ζητάει
Κοιτα εγω το εβγαλα απο το Bode και μου βγηκε 7.07 περιπου.. Σε προηγουμενα ποστ βεβαια το βγαζουν 6.53... Αυτο οφειλεται στο οτι εγω το πηρα απο το Bode ενω εκει πηραν τον τυπο |A(jωc)|, μονο που δεν ελαβαν τον πολο στο -20.. Τωρα αν θες αναλυτικες πραξεις με το Bode τις εχω..
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Avraam on February 02, 2015, 23:17:26 pm
Όποιος έχει λύσει θέμα 2ο σεπτέμβριο 2013 ας που πει πως στο καλό θα βγάλω την wc που ζητάει
Κοιτα εγω το εβγαλα απο το Bode και μου βγηκε 7.07 περιπου.. Σε προηγουμενα ποστ βεβαια το βγαζουν 6.53... Αυτο οφειλεται στο οτι εγω το πηρα απο το Bode ενω εκει πηραν τον τυπο |A(jωc)|, μονο που δεν ελαβαν τον πολο στο -20.. Τωρα αν θες αναλυτικες πραξεις με το Bode τις εχω..
Λοιπον με το Bode εχουμε και λεμε:
20log1000/(4*20) - 20logωc - 20logωc/4 = 0 και αν το προχωρησεις θα το βγαλεις
Με τον αλλο τροπο που σου λεω γινεται:
|A(jωc)| = |1000/((jωc)*(jωc+4))| = 1 το προχωρας κανονικα και βγαινει κοντα στο 6.53 που σου ειπα
Γενικα δεν ξερω τι φαση παιζει, αν γινονται δεκτα και τα 2.. Παντως στις ασκησεις νομιζω που εχει ανεβασμενες ο Exomag ασχολουνται με το αυτο το θεμα και βρισκει τις γωνιες και με τους 2 τροπους.. Απλα ο πρωτο ειναι πιο προσεγγιστικος νομιζω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 02, 2015, 23:22:42 pm
Όποιος έχει λύσει θέμα 2ο σεπτέμβριο 2013 ας που πει πως στο καλό θα βγάλω την wc που ζητάει
Κοιτα εγω το εβγαλα απο το Bode και μου βγηκε 7.07 περιπου.. Σε προηγουμενα ποστ βεβαια το βγαζουν 6.53... Αυτο οφειλεται στο οτι εγω το πηρα απο το Bode ενω εκει πηραν τον τυπο |A(jωc)|, μονο που δεν ελαβαν τον πολο στο -20.. Τωρα αν θες αναλυτικες πραξεις με το Bode τις εχω..
Λοιπον με το Bode εχουμε και λεμε:
20log1000/(4*20) - 20logωc - 20logωc/4 = 0 και αν το προχωρησεις θα το βγαλεις
Με τον αλλο τροπο που σου λεω γινεται:
|A(jωc)| = |1000/((jωc)*(jωc+4))| = 1 το προχωρας κανονικα και βγαινει κοντα στο 6.53 που σου ειπα
Γενικα δεν ξερω τι φαση παιζει, αν γινονται δεκτα και τα 2.. Παντως στις ασκησεις νομιζω που εχει ανεβασμενες ο Exomag ασχολουνται με το αυτο το θεμα και βρισκει τις γωνιες και με τους 2 τροπους.. Απλα ο πρωτο ειναι πιο προσεγγιστικος νομιζω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 02:17:35 am
ωb>10rad/s
αρα τι ξερουμε για ωb;
οτι ειναι η συχνοτητα για την οποια ισχυει οτι |Η(jωb)|= 0.707H(0)
μπορεις να βαλεις οριακα ωb=10 rad/sec και να βγαλεις ενα οριακο Κ
Επισης αλλος τροπος ειναι να δουλεψεις γνωριζοντας οτι ωc<ωb και να πας με το |Η(jωc)|=1
Υ.Σ.:Η H() ειναι του ανοιχτου βροχου
αρα τι ξερουμε για ωb;
οτι ειναι η συχνοτητα για την οποια ισχυει οτι |Η(jωb)|= 0.707H(0)
μπορεις να βαλεις οριακα ωb=10 rad/sec και να βγαλεις ενα οριακο Κ
Επισης αλλος τροπος ειναι να δουλεψεις γνωριζοντας οτι ωc<ωb και να πας με το |Η(jωc)|=1
Υ.Σ.:Η H() ειναι του ανοιχτου βροχου
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on February 03, 2015, 12:00:11 pm
Έχετε καμιά ιδέα για το πως να κάνω στο θέμα 2 του Γενάρη 11, το σ > 4 . Σίγουρα με ΓΤΡ, αλλά έχω δοκιμάσει τα πάντα και αυτός ο πόλος στο 0 που χρειάζεται, με το μηδενικό στο 2 απλά είναι "σκέτος πονοκέφαλος".
Κάπου ειπώθηκε ότι είναι λάθος... Παρόλα αυτά,αν θες να προσπαθήσεις κάποια λύση, το κόλπο είναι νομίζω να ωθήσεις τον πόλο του ΣΚΒ πολύ κοντά στο 2 για κάποιο μεγάλο Κ..Τότε ο συντελεστής του αντίστοιχου εκθετικου θα είναι πολύ μικρός και ο πόλος θα εξουδετερωθεί σχεδόν από το αντίστοιχο μηδενικό. Άρα δε θα έχει τον κυρίαρχο ρόλο στην βηματικη απόκριση (θέλει και λίγο matlab βέβαια για το πόσο κοντά στο 2...)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Αλντεμπαράν on February 03, 2015, 12:40:22 pm
Υπάρχει κάποια σειρά με την οποία εξετάζουμε τις διάφορες προδιαγραφές στα θέματα σχεδίασης ;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 12:53:47 pm
σεπτεμβρης 2008
να ρωτησω αν θελουμε να παρουμε σφαλμα αναδρασης και δεν εχουμε μοναδιαια αναδραση ο τυπος θα ναι ετσι;
E(s)=V(s)/(1+H1(s)*H2(s))
oπου H1(s) του ευθυ κλαδου και H2(s) της αναδρασης;
να ρωτησω αν θελουμε να παρουμε σφαλμα αναδρασης και δεν εχουμε μοναδιαια αναδραση ο τυπος θα ναι ετσι;
E(s)=V(s)/(1+H1(s)*H2(s))
oπου H1(s) του ευθυ κλαδου και H2(s) της αναδρασης;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Αλντεμπαράν on February 03, 2015, 13:47:13 pm
Για το σφάλμα ανάδρασης:εξαρτάται από το κύκλωμα, Για το συγκεκριμένο εγώ κάνω
e=V-Y
οπου Y=F*H1 = (V-Y*H2)*H1=> Y(1+H1H2)=VH1 => Y= H1/(1+H1H2) * v
άρα e=V(1-H1/(1+H1H2))
Tότε το σφάλμα θέσης βγαίνει ess=lim[ 1- H1/(1+H1H2))] για s->0
e=V-Y
οπου Y=F*H1 = (V-Y*H2)*H1=> Y(1+H1H2)=VH1 => Y= H1/(1+H1H2) * v
άρα e=V(1-H1/(1+H1H2))
Tότε το σφάλμα θέσης βγαίνει ess=lim[ 1- H1/(1+H1H2))] για s->0
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 14:09:40 pm
ok θενξ!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 14:09:53 pm
Τελικά για το θέμα 1γ Σεπτεμβριο 2013 με το μηδενικό τι γίνεται? Που το τοποθετούμε και πως το εξηγούμε?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 14:24:26 pm
θελουμε να δημιουργηθει μια ασυμπτωτη καπου μετα το -7 και πριν το -12 για να παει εκει ο κλαδος γιατι ετσι για μεγαλες συχνοτητες το πραγματικο μερος θα ναι μεγαλυτερο του 8 (καταπολυτη τιμη)
ετσι πηγα στο ΟΑ (ασυμπωτη) και ειδα οτι για να χουμε ασυμπτωτη πχ στο -9 πρεπει το μηδενικο να ναι στο -12
αρα το βαλα εκει
παρε και ενα διαγραμμα δωρο
(http://i.imgur.com/FzU63zK.jpg)
ετσι πηγα στο ΟΑ (ασυμπωτη) και ειδα οτι για να χουμε ασυμπτωτη πχ στο -9 πρεπει το μηδενικο να ναι στο -12
αρα το βαλα εκει
παρε και ενα διαγραμμα δωρο
(http://i.imgur.com/FzU63zK.jpg)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 14:30:10 pm
θελουμε να δημιουργηθει μια ασυμπτωτη καπου μετα το -7 και πριν το -12 για να παει εκει ο κλαδος γιατι ετσι για μεγαλες συχνοτητες το πραγματικο μερος θα ναι μεγαλυτερο του 8 (καταπολυτη τιμη)
ετσι πηγα στο ΟΑ (ασυμπωτη) και ειδα οτι για να χουμε ασυμπτωτη πχ στο -9 πρεπει το μηδενικο να ναι στο -12
αρα το βαλα εκει
παρε και ενα διαγραμμα δωρο
(http://i.imgur.com/FzU63zK.jpg)
ετσι πηγα στο ΟΑ (ασυμπωτη) και ειδα οτι για να χουμε ασυμπτωτη πχ στο -9 πρεπει το μηδενικο να ναι στο -12
αρα το βαλα εκει
παρε και ενα διαγραμμα δωρο
(http://i.imgur.com/FzU63zK.jpg)
οκ στην ίδια λογική κινούμαστε
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 14:52:04 pm
και για θέμα 2.γ και δ πάλι από Σεπτέμβριο 2013?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 14:59:44 pm
και για θέμα 2.γ και δ πάλι από Σεπτέμβριο 2013?
Αρχικά το ωc βγαίνει 7.Από το διάγραμμα φαίνεται ότι το καθορίζουν οι όροι πριν το 10.Άρα αν βάλεις ένα μηδενικό >= 10.Το ωc δεν θα αλλάξει.Οπότε η γωνιά θα είναι η ίδια + arctan(ωc/μ) άρα μεγαλώνει,άρα το κέρδος φάσης αυξάνεται.Βάζεις ένα μ πχ 10 και βλέπεις ότι όντως το κέρδος φάσης βγαίνει μεγαλύτερο από 40,οπότε είσαι κομπλέ
Μόλις το βάλεις βλέπεις ότι αν αθροίσεις τις μεγαλύτερες γωνίες που δίνουν οι όροι (κάθε ένας (s+a) δίνει +-90 αναλόγως αν είναι αριθμητή ή παρονομαστή) το αποτέλεσμα βγαίνει οριακά -180.και αφού οριακά βγαίνει -180 το κέρδος είναι άπειρο
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 15:03:43 pm
και για θέμα 2.γ και δ πάλι από Σεπτέμβριο 2013?
Αρχικά το ωc βγαίνει 7.Από το διάγραμμα φαίνεται ότι το καθορίζουν οι όροι πριν το 10.Άρα αν βάλεις ένα μηδενικό >= 10.Το ωc δεν θα αλλάξει.Οπότε η γωνιά θα είναι η ίδια + arctan(ωc/μ) άρα μεγαλώνει,άρα το κέρδος φάσης αυξάνεται.Βάζεις ένα μ πχ 10 και βλέπεις ότι όντως το κέρδος φάσης βγαίνει μεγαλύτερο από 40,οπότε είσαι κομπλέ
Το ματλαβ διαφωνεί μαζί σου όπως και εγώ. Αν βάλεις ένα μηδενικό και πας να ξανακάνεις bode θα σου αλλάξει το bode και θα σου αλλάξει και το wc. Και βασικά έβαλα ένα μηδενικό στο δέκα και βρηκα περιθώριο φάσης και βγαίνει περλιπου 30. Από την άλλη αν βάλω το μηδενικό πολύ κοντά στο 0 ( για να ακυρώσω τον πόλο ) πχ στο 0.5 είμαι κομπλέ.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 15:18:06 pm
και για θέμα 2.γ και δ πάλι από Σεπτέμβριο 2013?
Αρχικά το ωc βγαίνει 7.Από το διάγραμμα φαίνεται ότι το καθορίζουν οι όροι πριν το 10.Άρα αν βάλεις ένα μηδενικό >= 10.Το ωc δεν θα αλλάξει.Οπότε η γωνιά θα είναι η ίδια + arctan(ωc/μ) άρα μεγαλώνει,άρα το κέρδος φάσης αυξάνεται.Βάζεις ένα μ πχ 10 και βλέπεις ότι όντως το κέρδος φάσης βγαίνει μεγαλύτερο από 40,οπότε είσαι κομπλέ
Το ματλαβ διαφωνεί μαζί σου όπως και εγώ. Αν βάλεις ένα μηδενικό και πας να ξανακάνεις bode θα σου αλλάξει το bode και θα σου αλλάξει και το wc. Και βασικά έβαλα ένα μηδενικό στο δέκα και βρηκα περιθώριο φάσης και βγαίνει περλιπου 30. Από την άλλη αν βάλω το μηδενικό πολύ κοντά στο 0 ( για να ακυρώσω τον πόλο ) πχ στο 0.5 είμαι κομπλέ.
Ναι τώρα που το κανα διαφορετικό βγαίνει,γιατί το matlab το κάνει κανονικά και όχι με τις προσεγγίσεις που κάνουμε εμείς.Δηλαδή με μηδενικό στο 10 το ωc δεν αλλάζει με την προσέγγιση ότι ο όρος (s+10) δίνει μηδέν πλάτος πριν το 10.τώρα αν υποθέσουμε ότι το πάμε έτσι το περιθώριο φάσης βγαίνει πάνω από 40 αφού μόνο το arctan(7.09/10) κάνει 35
Θεμα 2ο Σεπτ, 2014 πως βρίσκουμε τους πόλους? Γιατί εγω έβαλα Κ=15,47 και μετά πήρα την Χ.Ε. αλλά δε μου βγήκαν αυτοί οι μιγαδικοί πόλοι.
Απ' ότι θυμάμαι έβγαινε κ=15.47 και οι πόλοι στο [-14.57+-i*sqrt(48.26)]/2 και αυτός που γνωρίζεις στο -1.9. Άρα όλοι οι πόλοι είναι σημαντικοί.
ναι έτσι το κανα και γώ,και μου βγήκαν αυτοί.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 15:24:21 pm
και για θέμα 2.γ και δ πάλι από Σεπτέμβριο 2013?
Αρχικά το ωc βγαίνει 7.Από το διάγραμμα φαίνεται ότι το καθορίζουν οι όροι πριν το 10.Άρα αν βάλεις ένα μηδενικό >= 10.Το ωc δεν θα αλλάξει.Οπότε η γωνιά θα είναι η ίδια + arctan(ωc/μ) άρα μεγαλώνει,άρα το κέρδος φάσης αυξάνεται.Βάζεις ένα μ πχ 10 και βλέπεις ότι όντως το κέρδος φάσης βγαίνει μεγαλύτερο από 40,οπότε είσαι κομπλέ
Το ματλαβ διαφωνεί μαζί σου όπως και εγώ. Αν βάλεις ένα μηδενικό και πας να ξανακάνεις bode θα σου αλλάξει το bode και θα σου αλλάξει και το wc. Και βασικά έβαλα ένα μηδενικό στο δέκα και βρηκα περιθώριο φάσης και βγαίνει περλιπου 30. Από την άλλη αν βάλω το μηδενικό πολύ κοντά στο 0 ( για να ακυρώσω τον πόλο ) πχ στο 0.5 είμαι κομπλέ.
Ναι τώρα που το κανα διαφορετικό βγαίνει,γιατί το matlab το κάνει κανονικά και όχι με τις προσεγγίσεις που κάνουμε εμείς.Δηλαδή με μηδενικό στο 10 το ωc δεν αλλάζει με την προσέγγιση ότι ο όρος (s+10) δίνει μηδέν πλάτος πριν το 10.τώρα αν υποθέσουμε ότι το πάμε έτσι το περιθώριο φάσης βγαίνει πάνω από 40 αφού μόνο το arctan(7.09/10) κάνει 35
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: giwrgosbg on February 03, 2015, 15:36:47 pm
Παιδια πως βγαινει το ts οταν εχω κρατησει μονο εναν κυριαρχο πολο;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 16:09:47 pm
ΛΥΣΕΙΣ σεπτεμβριος 2013
Αν βρείτε λάθη please πείτε μου
Αν βρείτε λάθη please πείτε μου
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 17:56:43 pm
Αν σε ένα διάγραμμα Bode δεν έχω ωc τότε τι μπορώ να πω για οτ περιθώριο φάσης;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: DarkPassenger on February 03, 2015, 18:04:40 pm
Αν σε ένα διάγραμμα Bode δεν έχω ωc τότε τι μπορώ να πω για οτ περιθώριο φάσης;;
+1πχ θεμα 1 ιαν. 2013
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 18:08:57 pm
δεν μπορεις να το βρεις καπως;
απο |Η(jωc)|=1
απο |Η(jωc)|=1
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:09:45 pm
Αν βγαίνει αδύνατη.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 18:10:32 pm
Αν σε ένα διάγραμμα Bode δεν έχω ωc τότε τι μπορώ να πω για οτ περιθώριο φάσης;;
+1πχ θεμα 1 ιαν. 2013
Υπάρχει ωc, απλα είναι πιο μικρο απο την πρωτη τιμή που κοιτάς (0.1).Στο θέμα του γενάρη βγαίνει 0.067
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 18:12:42 pm
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:14:17 pm
Σε ένα άλλο θέμα που λύνω μου βγήκε τέτοιο πράμα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: heavy melon on February 03, 2015, 18:20:27 pm
Αν σε ένα διάγραμμα Bode δεν έχω ωc τότε τι μπορώ να πω για οτ περιθώριο φάσης;;
+1πχ θεμα 1 ιαν. 2013
Υπάρχει ωc, απλα είναι πιο μικρο απο την πρωτη τιμή που κοιτάς (0.1).Στο θέμα του γενάρη βγαίνει 0.067
ξεκινάς αντί από log0.1 από log0.01 και θα σου εμφανιστεί κ το που τέμνει τον άξονα χ'χ
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 18:21:33 pm
psira
κανε πινακακι για το μποντε και δες που αλλαζουν προσημο τα κερδη
καπου εκει ειναι το ωc
ψαξου λιγο με τις εξισωσεις και θα το βρεις
κανε πινακακι για το μποντε και δες που αλλαζουν προσημο τα κερδη
καπου εκει ειναι το ωc
ψαξου λιγο με τις εξισωσεις και θα το βρεις
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:25:34 pm
Έχω δύο συζυγείς μιγαδικούς μηδενικά που με τραβάνε προς τα πάνω γι αυτό δεν υπάρχει ωc.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 18:26:45 pm
ε αμα σε τραβανε δεν μηδενιζεται το κερδος ποτε
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:27:37 pm
Thats what i am saying darlin . Ποιο το περιθώριο φάσης τότε;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 03, 2015, 18:29:10 pm
Έχω δύο συζυγείς μιγαδικούς μηδενικά που με τραβάνε προς τα πάνω γι αυτό δεν υπάρχει ωc.
Δηλαδή ο βαθμός του αριθμητή της ΣΜ είναι μεγαλύτερος από τον βαθμό του παρανομαστή; Είσαι σίγουρος γι' αυτό;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:30:09 pm
Ίσος. Με ελεγκτη PID
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Exomag on February 03, 2015, 18:39:37 pm
Ίσος. Με ελεγκτη PID
Ο ελεγκτής PID όμως θα εφαρμοστεί σε κάποιο σύστημα, δε θα είναι μόνος του. Δώσε συγκεκριμένο παράδειγμα/άσκηση/θέμα άμα θες να γίνεις σαφής.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 18:41:34 pm
Πολύ ευχαρίστως. Θέμα 2 Φεβρουάριος του 2008, έβαλα PID γιατί ο σερ Πετρίδης θέλει περιθώριο φάσης τη μάνα του.
Έπέλεξα τους πόλους του ελεγκτή στο -10 και -8. Κέρδος έβαλα 1.
Έπέλεξα τους πόλους του ελεγκτή στο -10 και -8. Κέρδος έβαλα 1.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 19:03:24 pm
Πολύ ευχαρίστως. Θέμα 2 Φεβρουάριος του 2008, έβαλα PID γιατί ο σερ Πετρίδης θέλει περιθώριο φάσης τη μάνα του.
Έπέλεξα τους πόλους του ελεγκτή στο -10 και -8. Κέρδος έβαλα 1.
Έπέλεξα τους πόλους του ελεγκτή στο -10 και -8. Κέρδος έβαλα 1.
Αν βάλεις k(s+a)/s ελεγκτή νομιζω οτι βγαινει η μεγιστη γωνία της A(s) -90,αρα περιθώριο φασης πανω απο 90 παντα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 19:04:48 pm
Ή κάτι κάνω λάθος ή δεν είναι έτσι πως τα λές.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 19:13:15 pm
Ή κάτι κάνω λάθος ή δεν είναι έτσι πως τα λές.
Με αυτον τον ελεγκτή η Α(s) δεν έχει ενα μηδενικό και 2 πόλους;
Αν ναι,νομιζω οτι η μέγιστη γωνία είναι 90-180=-90 αρα θm=180-90=90 στην χειρότερη
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 19:14:48 pm
Κάτσε ρε το s+a το έφαγες;; Και είναι στο Θέμα 2 Φεβρουάριος του 2008 αυτός ο ελεγκτής.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 19:17:32 pm
Όχι,αφού απο μονο του δεν έχει μηδενικά,με τον ελεγκτή έχει 1.
A(s)=8k(s+a)/s(s+1)
A(s)=8k(s+a)/s(s+1)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 19:21:25 pm
E Ωραία. στις 180 το μηδενικο προσθέτει φάση ο ολοκλρηωτής αφαιρεί 90 και το s+1 αφαίρει φάση. Γιατί είσαι πάντα πάνω από 90;;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 19:39:39 pm
Ναι εχεις δίκιο δεν ειναι καλη η εξήγηση.Παρόλα αυτα, αν δεν λάβεις υπ όψιν το κριτήριο αυτό αλλά λάβεις τα αλλά,(πχ τελικά έβαλα κ=10 και α=9) τυχαίνει να βγαίνει μεγαλυτερο απο 80 :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 19:44:20 pm
Τα άλλα κριτήρια ικανοποιούνται όμως;;
Αν δεν έχω φαει κάτι κάπου,ναι
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 19:50:07 pm
To ωc μου βγαίνει 80,5 συμφωνείς;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on February 03, 2015, 19:55:04 pm
Τα άλλα κριτήρια ικανοποιούνται όμως;;
Γενικά αυτά που πρότεινε ο Ναπολέων μοιάζουν λογικά... Αν δεν ικανοποιούνται, πάρε μεγαλύτερο Κ. Κι αυτό γιατί περιθώριο κέρδους θα χεις άπειρο ούτως ή αλλως με 2 πόλους κι ένα μηδενικό. Αν το μηδενικό το τοποθετήσεις αριστερότερα του -8 από ΓΤΡ κάποια στιγμή θα ναι και οι 2 πόλοι του ΣΚΒ αριστερά του -8, άρα καλός χρόνος αποκατάστασης. Επίσης για τις διαταραχές θες το διαγραμμα Bode ψηλά (συγκεκριμένα |A(j1)|>100 νομίζω), άρα μεγάλο Κ. Για το μικρό σφάλμα ταχύτητας πάλι μεγάλο Κ. Τέλος, αν πάρεις μεγάλο Κ θα πας πιο δεξιά την ωc, θα δρα και το μηδενικό και γενικά θα πλησιάζεις προς τις -90 μοίρες στο Bode φάσης (άρα 90 περιθώριο).
Ε, άρα αφού δεν υπάρχει περιορισμός για το Κ, πάρτο αρκετά μεγάλο για να ικανοποιηθούν κάποια στιγμή. Άνω όριο (πέρα από τη λογική) το πρόβλημα δε σου επιβάλλει.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 19:58:00 pm
Ρε Βασίλη μεγάλο Κέρδος δε σου μειώνει το περιθώριο φάσης;;;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Napoleon on February 03, 2015, 20:02:30 pm
Μου βγοαινει 85.για τις γωνίες πήρα arctan και όχι τις προσεγγίσεις του βιβλίου. Εδώ όσο μεγαλυτερο ωc τόσο το καλυτερο γιατί έτσι μειωνεται η διαφορα στις γωνίες του μηδενικού και του πόλου στο 1 και μένει μονο το -90 του πόλου στο μηδέν
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on February 03, 2015, 20:02:58 pm
Ρε Βασίλη μεγάλο Κέρδος δε σου μειώνει το περιθώριο φάσης;;;
Γιατί? Σκέψου τα Bode. Της φάσης ξεκινά από -90 λόγω του ολοκληρωτή, πάει προς το -180 λόγω του πόλου που είναι νωρίς και στη συνέχεια αρχίζει να ξανανεβαίνει προς το -90 λόγω του μηδενικού.
Αν αυξήσεις το Κ, το Bode φάσης δεν αλλάζει. Το Bode πλάτους ανεβαίνει όλο προς τα πάνω και στέλνεις την ωc προς τα δεξιά. Ε, όσο πιο δεξιά η ωc (αν μιλάμε για νούμερα μεγαλύτερα του μηδενικού τουλάχιστον) τόσο καλύτερα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: AckermanMik on February 03, 2015, 20:18:29 pm
Ευχαριστώ σας. Το προσπαθώ από το πρωί και λέω μαλακίες. Επιτέλους βγήκε.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: soso on February 03, 2015, 21:37:33 pm
Στο 3ο θέμα σεπτ. 12 μας ζητάει να υπολογίσουμε περιθώριο κερδους. Θα πω ότι είναι απειρο γιατί ΟΑ <0 η θα κάνω Ρουθ και θα πω gm =24?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on February 03, 2015, 21:44:54 pm
Στο 3ο θέμα σεπτ. 12 μας ζητάει να υπολογίσουμε περιθώριο κερδους. Θα πω ότι είναι απειρο γιατί ΟΑ <0 η θα κάνω Ρουθ και θα πω gm =24?
Δεν έχει σχέση το ΟΑ, έχεις 3 ασύμπτωτες, οπότε για μεγάλα Κ κάποια στιγμή θα φύγεις στην αστάθεια. Αν ήταν 2, τότε έχει νόημα γιατί ξες για μεγάλο Κ, πόσο θα είναι το πραγματικό μέρος των πόλων.
Μπορείς να το σκεφτείς και από το Bode: αφού κάποια στιγμή θα φτάσεις στις -180 στο Bode φάσης (ξεκινάς από -90 και φτάνεις σε απειρο ω στο -270), θα μετρήσεις εκεί πέρα από το Bode πλάτους το (πεπερασμένο) περιθώριο κέρδους. Βέβαια ποτέ δε το βρίσκουμε, έτσι, αλλά με Routh και πράγματι βγαίνει 24 στο α.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 21:53:27 pm
Στο 3ο θέμα σεπτ. 12 μας ζητάει να υπολογίσουμε περιθώριο κερδους. Θα πω ότι είναι απειρο γιατί ΟΑ <0 η θα κάνω Ρουθ και θα πω gm =24?
το περιθωριο κερδους 20log24 δεν ειναι;Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on February 03, 2015, 21:56:32 pm
Στο 3ο θέμα σεπτ. 12 μας ζητάει να υπολογίσουμε περιθώριο κερδους. Θα πω ότι είναι απειρο γιατί ΟΑ <0 η θα κάνω Ρουθ και θα πω gm =24?
το περιθωριο κερδους 20log24 δεν ειναι;Από τη στιγμή που δε ζητά το κέρδος σε db γιατί να το κάνεις αυτό? Απλώς 24.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Πάτρικ Αστέρης on February 03, 2015, 21:58:08 pm
νταξ οκ
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Eilex on February 03, 2015, 22:56:22 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 23:12:31 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Eilex on February 03, 2015, 23:21:17 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Ναι μπαίνει σαν (s+12) άλλο λέω,ουσιαστικά λέω ότι βάζεις (s+12) αλλά όταν θεωρείς ότι δεν επηρεάζει το wc και πας να απλοποιήσεις την συνάρτηση σου μένει το 12 σαν συντελεστής στο κέρδος ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 23:24:37 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Ναι μπαίνει σαν (s+12) άλλο λέω,ουσιαστικά λέω ότι βάζεις (s+12) αλλά όταν θεωρείς ότι δεν επηρεάζει το wc και πας να απλοποιήσεις την συνάρτηση σου μένει το 12 σαν συντελεστής στο κέρδος ?
Δεν καταλαβαίνω. Όταν πας να απλοποιήσεις την συνάρτηση για να την κάνεις τι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Eilex on February 03, 2015, 23:31:07 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Ναι μπαίνει σαν (s+12) άλλο λέω,ουσιαστικά λέω ότι βάζεις (s+12) αλλά όταν θεωρείς ότι δεν επηρεάζει το wc και πας να απλοποιήσεις την συνάρτηση σου μένει το 12 σαν συντελεστής στο κέρδος ?
Δεν καταλαβαίνω. Όταν πας να απλοποιήσεις την συνάρτηση για να την κάνεις τι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Give_Life_Back on February 03, 2015, 23:39:26 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Ναι μπαίνει σαν (s+12) άλλο λέω,ουσιαστικά λέω ότι βάζεις (s+12) αλλά όταν θεωρείς ότι δεν επηρεάζει το wc και πας να απλοποιήσεις την συνάρτηση σου μένει το 12 σαν συντελεστής στο κέρδος ?
Δεν καταλαβαίνω. Όταν πας να απλοποιήσεις την συνάρτηση για να την κάνεις τι?
Όκ κατάλαβα τι λες. Θεωρώντας ότι βάζεις το μηδενικό εκεί ώστε να μην επιρρεάζει την wc, η καινούργια σου wc παραμένει ίδια. Στην πραγματικότητα ( και αν το βάλεις στο matlab θα το δεις) η καινούργια wc θα είναι διαφορετική. Όταν εγώ πάω πχ να υπολογίσω την καινούργια wc ( δεν ξέρω γιατί το θες ) θα παραλήψω όλο το όρο σαν να μην υπάρχει καθόλου. Δεν ξέρω αν είναι σωστό ααλλά σου είπα ότι το στηρίζω στο σκεπτικό ότι αφού έκανα προσέγγιση για να μην αλλάξει η wc δεν καταλαβαίνω γιατί να την ξαναυπολογίσω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Eilex on February 03, 2015, 23:59:03 pm
Στον σεπτέμβριο του 13 στο 2ο θέμα εκεί που προσθέτει μηδενικό ώστε να αυξηθεί το περιθώριο φάσης.Άμα πάρεις το μηδενικό πέρα του wc ώστε να μην το επηρεάζει, ουσιαστικά δεν πρέπει να πάρεις το μ σαν συντελεστή μετά?Δηλαδή άμα έχεις 1000(s+μ)/s(s+4)(s+20) άμα θεωρήσεις ότι έχεις wc = 6,7rad/s και πεις ότι θέτεις το μ = 12 για να μην επηρέαζει το wc δεν πρέπει να πάρει η συνάρτηση την μορφή 1000*12/s(s+4)(s+20) ? Ή αυτό συμβαίνει μόνο όταν μιλάμε για πόλους και όχι για μηδενικά?
Αν απλά βάλεις στον αριθμητή της συνάρτησης ένα 12 δεν προσθέτεις μηδενικό. Έβαλες απλά έναν σταθερό όρο που συνεισφέρει παντού. τα μηδενικά πρέπει να μπουν στον αριθμητή στην μορφή (s+12)
Ναι μπαίνει σαν (s+12) άλλο λέω,ουσιαστικά λέω ότι βάζεις (s+12) αλλά όταν θεωρείς ότι δεν επηρεάζει το wc και πας να απλοποιήσεις την συνάρτηση σου μένει το 12 σαν συντελεστής στο κέρδος ?
Δεν καταλαβαίνω. Όταν πας να απλοποιήσεις την συνάρτηση για να την κάνεις τι?
Όκ κατάλαβα τι λες. Θεωρώντας ότι βάζεις το μηδενικό εκεί ώστε να μην επιρρεάζει την wc, η καινούργια σου wc παραμένει ίδια. Στην πραγματικότητα ( και αν το βάλεις στο matlab θα το δεις) η καινούργια wc θα είναι διαφορετική. Όταν εγώ πάω πχ να υπολογίσω την καινούργια wc ( δεν ξέρω γιατί το θες ) θα παραλήψω όλο το όρο σαν να μην υπάρχει καθόλου. Δεν ξέρω αν είναι σωστό ααλλά σου είπα ότι το στηρίζω στο σκεπτικό ότι αφού έκανα προσέγγιση για να μην αλλάξει η wc δεν καταλαβαίνω γιατί να την ξαναυπολογίσω.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: boone on June 26, 2015, 00:04:01 am
Θέμα 1 Γιούλης του '09 κανείς;
με ποιόν τρόπο το κάνετε;
με Routh?
με ποιόν τρόπο το κάνετε;
με Routh?
Νομίζω λένε τη λύση στις προηγούμενες σελίδες. Είναι out of my comfort zone κι ελπίζω σε κάτι από τα πιο πρόσφατα θέματα! Ας προσευχηθούμε όλοι :P
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: vasilis94 on August 19, 2015, 15:25:00 pm
Ανέβασα κάποιες λύσεις από πέρυσι και πιο πριν στα downloads... Ελπίζω να φανούν χρήσιμα και να μην έχουν (πολλά) λάθη!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ragnar Lothbrok on August 19, 2015, 22:37:54 pm
Ανέβασα κάποιες λύσεις από πέρυσι και πιο πριν στα downloads... Ελπίζω να φανούν χρήσιμα και να μην έχουν (πολλά) λάθη!
Σου έχω ξαναπεί ότι είσαι ΤΕΡΑΣΤΙΟΣ; Νομίζω στο χω ξαναπεί. Δεν πειράζει, ακόμα μια φορά. ΕΙΣΑΙ ΤΕΡΑΣΤΙΟΣ!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: kiarimN@@b on August 30, 2015, 00:05:29 am
Στο θέμα 1γ Σεπτέμβριος 2013:
Υπάρχει κάποιος συγκεκριμένος λόγος που επιλέγω μηδενικό στην περιοχή (-18,-7) και όχι στην περιοχή αριστερά του -18?
Καταλαβαίνω ότι δε μπορώ να πάρω μηδενικό πολύ κοντά σε πόλο γιατί στην ουσία τον απαλείφω, αλλά γιατί όχι πολύ μακριά;
Υπάρχει κάποιος συγκεκριμένος λόγος που επιλέγω μηδενικό στην περιοχή (-18,-7) και όχι στην περιοχή αριστερά του -18?
Καταλαβαίνω ότι δε μπορώ να πάρω μηδενικό πολύ κοντά σε πόλο γιατί στην ουσία τον απαλείφω, αλλά γιατί όχι πολύ μακριά;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 23, 2016, 22:58:42 pm
Σε πολλα λυμενα θεματα ζηταει την μορφη 1+κΑ(s) αυτο ομως δεν ειναι το ΧΠ της ΣΜΚΒ ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Andromedas on January 23, 2016, 23:08:48 pm
όχι ακριβώς το A(s) είναι του ανοικτού βρόγχου... συνήθως είναι το ίδιο όταν κλείσεις το βρόχο Α(s) =G(s)F(s) όπου Y/X=(G(s))/(1+G(s)F(s)). Περίμενε και ανεβάζω το 1ο)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Vlassis on January 24, 2016, 00:11:20 am
Σεπτεμβριος 2012, θεμα 2ο, το περιθωριο κερδους ειναι το Κ που βρισκουμε απο το Routh ή υπολογίζεται διαφορετικά επειδή δεν έχω αρνητική μοναδιαία ανάδραση ;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Andromedas on January 24, 2016, 00:50:35 am
Σεπτεμβριος 2012, θεμα 2ο, το περιθωριο κερδους ειναι το Κ που βρισκουμε απο το Routh ή υπολογίζεται διαφορετικά επειδή δεν έχω αρνητική μοναδιαία ανάδραση ;
Δεν έχει σημασία η ανάδραση εκτός εάν έχεις κάποιον έτοιμο τύπο, διότι βγάζεις το χαρακτηριστικό οποία ανάδραση και να χρησιμοποιήσεις (μάλλον αλλάζει το A(s) αφού αλλάζει η ανάδραση αν και στο συγκεκριμένο δεν νομίζω να έχει κάτι τετοίο). Το Routh του χαρακτηριστικού σου λέει από Κ μέχρι τάδε Κ δεν αλλάζει το πρόσημο. Εγώ βρίσκω το Α(s) και από αυτό βρίσκοντας την κρίσιμη συχνότητα δηλαδή την w όπου Im(Α(jw))=0 και μετά Κ=-20log|A(jw)| σε db άλλα είναι μανούρα ο τρόπος μου (σελ 291 παρασκευοπουλος).Μετά όμως σου ζητάει κάτι αντίστοιχο το θέμα 8))Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Ancient on January 24, 2016, 03:11:36 am
Σεπτεμβριος 2012, θεμα 2ο, το περιθωριο κερδους ειναι το Κ που βρισκουμε απο το Routh ή υπολογίζεται διαφορετικά επειδή δεν έχω αρνητική μοναδιαία ανάδραση ;
Θα πρέπει να πάρεις το χαρακτηριστικό πολυώνυμο του συστήματος κλειστού βρόχου και να κάνεις Routh εκεί.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 24, 2016, 23:28:28 pm
Η λυση του θεματος 1 ιανουαριος 2013 μηπως ειναι λαθος ??
το πινακακι εχει λαθος τιμες Db νομιζω
το πινακακι εχει λαθος τιμες Db νομιζω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: pol on January 25, 2016, 11:49:41 am
παιδιά SOS ξέρει κάποιος το σκεπτικό για το θέμα 2 του 2013 στο γ ερώτημα που λέει να τοποθετήσουμε μηδενικό ώστε το περιθώριο φάσης να είναι μεγαλύτερο των 40;Πως το διαλέγουμε;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Escobar on January 25, 2016, 12:35:09 pm
παιδιά SOS ξέρει κάποιος το σκεπτικό για το θέμα 2 του 2013 στο γ ερώτημα που λέει να τοποθετήσουμε μηδενικό ώστε το περιθώριο φάσης να είναι μεγαλύτερο των 40;Πως το διαλέγουμε;
εγώ όπως το έχει στα λυμένα θα το έκανα, trial and error. Το βάζεις κάπου που σου φαίνεται λογικό, βρίσκεις την ωc, βρίσκεις περιθώριο φάσης και αν σου κάνει το κρατάς. Μετά από μια, δυο άντε τρεις δοκιμές θα το βρεις, δεν υπάρχει περίπτωση
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 25, 2016, 12:59:31 pm
Η λυση του θεματος 1 ιανουαριος 2013 μηπως ειναι λαθος ??
το πινακακι εχει λαθος τιμες Db νομιζω
αυτο το ειδε κανεις την λυση του ?το πινακακι εχει λαθος τιμες Db νομιζω
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Gru on January 25, 2016, 13:01:46 pm
Η λυση του θεματος 1 ιανουαριος 2013 μηπως ειναι λαθος ??
το πινακακι εχει λαθος τιμες Db νομιζω
αυτο το ειδε κανεις την λυση του ?το πινακακι εχει λαθος τιμες Db νομιζω
ποιο σου βγαίνει διαφορετικά? και εγώ τόσο περίπου τα βρήκα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 25, 2016, 13:16:03 pm
Η λυση του θεματος 1 ιανουαριος 2013 μηπως ειναι λαθος ??
το πινακακι εχει λαθος τιμες Db νομιζω
αυτο το ειδε κανεις την λυση του ?το πινακακι εχει λαθος τιμες Db νομιζω
ποιο σου βγαίνει διαφορετικά? και εγώ τόσο περίπου τα βρήκα.
του 1/s ειναι σωστες και του κερδους στα αλλα βρισκω διαφορετικο π.χ στο μηδενικο (s/3 + 1)
Δεν ειναι 20log(s/3) ? οπου s = 3,4,7,8 ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Gru on January 25, 2016, 13:23:07 pm
ποιο σου βγαίνει διαφορετικά? και εγώ τόσο περίπου τα βρήκα.
του 1/s ειναι σωστες και του κερδους στα αλλα βρισκω διαφορετικο π.χ στο μηδενικο (s/3 + 1)
Δεν ειναι 20log(s/3) ? οπου s = 3,4,7,8 ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 25, 2016, 13:24:51 pm
ποιο σου βγαίνει διαφορετικά? και εγώ τόσο περίπου τα βρήκα.
του 1/s ειναι σωστες και του κερδους στα αλλα βρισκω διαφορετικο π.χ στο μηδενικο (s/3 + 1)
Δεν ειναι 20log(s/3) ? οπου s = 3,4,7,8 ?
δηλαδη π.χ στο ω = 4 το σ/3+1 γινεται 20log(4/3) =....2.49 σωστα ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Gru on January 25, 2016, 13:26:12 pm
ποιο σου βγαίνει διαφορετικά? και εγώ τόσο περίπου τα βρήκα.
του 1/s ειναι σωστες και του κερδους στα αλλα βρισκω διαφορετικο π.χ στο μηδενικο (s/3 + 1)
Δεν ειναι 20log(s/3) ? οπου s = 3,4,7,8 ?
δηλαδη π.χ στο ω = 4 το σ/3+1 γινεται 20log(4/3) =....2.49 σωστα ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: airguitar on January 25, 2016, 13:53:25 pm
κατι ακομα λυσεις σελιδα 20 θεμα 2 Ιανουαριος 2013 που λεει βρισκω το κ στο σημειο θλασης τι εννοει ακριβως ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Andromedas on January 25, 2016, 14:18:45 pm
κατι ακομα λυσεις σελιδα 20 θεμα 2 Ιανουαριος 2013 που λεει βρισκω το κ στο σημειο θλασης τι εννοει ακριβως ?
Βρίσκω χαρακτ pc(s) φέρνω στην μορφή που θέλει 1+Κ()=0 κάνω (dpc(s)/ds)=0 προφανώς το Κ διάφορο του μηδενός και βρίσκω τα πιθανά s όπου είναι τα πιθανά σημεία θλάσης. Έστω s1 s2 s3 πχ εάν είναι τριτοβάθμιο. Μέτα διαλέγω τα σημεία θλάσης βάση του διαγράμματος και τα αντικαθιστώ στο pc(s)=0 (πχ pc(s1)=0) και βρίσκω το Κ εάν είναι θετικό είμαι κομπλέ και το κρατάω. Σελ 49 έχω ανεβάσει κάτι παρόμοιο. sae1Sept2014.rar . Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 24, 2016, 17:05:54 pm
θεμα 1ο φεβρουαριος 2009
πως προκυπτουν τα σημεια τομης με τον Ιm αξονα στα +- j5 με βαση την λυση απτα downloads?
και στο wolfram που βαζω την εξισωση στο +- j5 τα δειχνει,δεν μπορω να καταλαβω ομως που εχω λαθος..
απτην εξισωση που βρισκω s4 + 17s3 +95s2 + (199+K)s +120+7K=0
αν κανω κριτηριο Routh μου βγαινει Κ=1416 στο οριο ευσταθειας και απτην χαρακτηριστικη της προηγουμενης
σειρας που προκυπτει η οριακη ασταθεια 17s3 + (199+1416)s=0 βγαινει s=0 η s=+- j9,74.
καποιος που να το εχει λυμενο?
πως προκυπτουν τα σημεια τομης με τον Ιm αξονα στα +- j5 με βαση την λυση απτα downloads?
και στο wolfram που βαζω την εξισωση στο +- j5 τα δειχνει,δεν μπορω να καταλαβω ομως που εχω λαθος..
απτην εξισωση που βρισκω s4 + 17s3 +95s2 + (199+K)s +120+7K=0
αν κανω κριτηριο Routh μου βγαινει Κ=1416 στο οριο ευσταθειας και απτην χαρακτηριστικη της προηγουμενης
σειρας που προκυπτει η οριακη ασταθεια 17s3 + (199+1416)s=0 βγαινει s=0 η s=+- j9,74.
καποιος που να το εχει λυμενο?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 24, 2016, 18:00:15 pm
μπορεις να ανεβασεις τα θεματα για στα downloads εχουν θεμα;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 00:56:01 am
μπορεις να ανεβασεις τα θεματα για στα downloads εχουν θεμα;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 01:02:59 am
το 2ο μερος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 01:04:48 am
και καποιες λυσεις
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 12:54:23 pm
θεμα 1ο φεβρουαριος 2009
πως προκυπτουν τα σημεια τομης με τον Ιm αξονα στα +- j5 με βαση την λυση απτα downloads?
και στο wolfram που βαζω την εξισωση στο +- j5 τα δειχνει,δεν μπορω να καταλαβω ομως που εχω λαθος..
απτην εξισωση που βρισκω s4 + 17s3 +95s2 + (199+K)s +120+7K=0
αν κανω κριτηριο Routh μου βγαινει Κ=1416 στο οριο ευσταθειας και απτην χαρακτηριστικη της προηγουμενης
σειρας που προκυπτει η οριακη ασταθεια 17s3 + (199+1416)s=0 βγαινει s=0 η s=+- j9,74.
καποιος που να το εχει λυμενο?
Νομιζω εχεις λαθος στην ΧΕ σουπως προκυπτουν τα σημεια τομης με τον Ιm αξονα στα +- j5 με βαση την λυση απτα downloads?
και στο wolfram που βαζω την εξισωση στο +- j5 τα δειχνει,δεν μπορω να καταλαβω ομως που εχω λαθος..
απτην εξισωση που βρισκω s4 + 17s3 +95s2 + (199+K)s +120+7K=0
αν κανω κριτηριο Routh μου βγαινει Κ=1416 στο οριο ευσταθειας και απτην χαρακτηριστικη της προηγουμενης
σειρας που προκυπτει η οριακη ασταθεια 17s3 + (199+1416)s=0 βγαινει s=0 η s=+- j9,74.
καποιος που να το εχει λυμενο?
Το εκανα τωρα και εβγαλα +- j4.9
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 14:09:24 pm
Νομιζω εχεις λαθος στην ΧΕ σου
Το εκανα τωρα και εβγαλα +- j4.9
μπορεις να γραψεις την ΧΕ που βγαζεις??Το εκανα τωρα και εβγαλα +- j4.9
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: geralt on August 25, 2016, 14:25:10 pm
και καποιες λυσεις
Τα συγκεκριμένα νομιζω είναι μεσα στα λαθη, ας επιβεβαιωσει κανεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 14:34:37 pm
μπορεις να γραψεις την ΧΕ που βγαζεις??
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 14:46:49 pm
Τα συγκεκριμένα νομιζω είναι μεσα στα λαθη, ας επιβεβαιωσει κανεις.
ναι γενικα υπαρχουν αρκετα λαθη,τα ειχα βρει στα downloadsαπλα καποιος ανεφερε οτι δεν λειτουργουν τα downloads
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 14:53:26 pm
εγω το ειχα πει αλλα αναφερομουν μονο στου 2009 :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 14:56:16 pm
και στην 3η σειρα βαζεις μονο το 4s2?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 14:59:08 pm
πωωω...και βγηκε τοσο καλο... :-\
Με αυτη την διορθωση βγαζουμε ιδια ΧΕ?
Με αυτη την διορθωση βγαζουμε ιδια ΧΕ?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 15:00:49 pm
πωωω...και βγηκε τοσο καλο... :-\
Με αυτη την διορθωση βγαζουμε ιδια ΧΕ?
ναι η ΧΕ βγαινει αυτη που ειχα γραψει,οποτε παλι καταληγω στο ιδιο αποτελεσμαΜε αυτη την διορθωση βγαζουμε ιδια ΧΕ?
χωρις να μπορω να βγαλω τα σημεια τομης με τον Im αξονα στα +- j5...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 15:02:20 pm
θα το ξαναδω σε λιγο
για το θεμα 2 φεβρ 2009 τελευταιο ερωτημα εχει κανεις καμια ιδεα;
για το θεμα 2 φεβρ 2009 τελευταιο ερωτημα εχει κανεις καμια ιδεα;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 15:12:56 pm
ναι η ΧΕ βγαινει αυτη που ειχα γραψει,οποτε παλι καταληγω στο ιδιο αποτελεσμα
χωρις να μπορω να βγαλω τα σημεια τομης με τον Im αξονα στα +- j5...
το βρηκα η ΧΕ ειναι σωστη απλα ειχα κανει αριθμητικο στην 2βαθμια του Κχωρις να μπορω να βγαλω τα σημεια τομης με τον Im αξονα στα +- j5...
βγαζεις Κ=236,93 και αν πας στην βοηθητικη βγαινει s=+-j5,06
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 15:14:11 pm
κομπλε..με γλιτωσες απο τις πραξεις
για το 2ο θεμα τελευταιο ερωτημα εχεις καμια ιδεα;
για το 2ο θεμα τελευταιο ερωτημα εχεις καμια ιδεα;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Andromedas on August 25, 2016, 15:19:50 pm
θα το ξαναδω σε λιγο
για το θεμα 2 φεβρ 2009 τελευταιο ερωτημα εχει κανεις καμια ιδεα;
κλασσική διαδικασία υπολογισμού ess για το θεμα 2 φεβρ 2009 τελευταιο ερωτημα εχει κανεις καμια ιδεα;
e=y-x αναλύεις σε δύο κλάσματα ένα σε x ένα σε d (που μάλλον είναι η διαταραχή το ρώτας πολύ πολύ, εκεί πάντως μπαίνει ο θόρυβος ... ).
θεώρημα επαλληλίας και 2 θττ για x και y
Θεώρημα ΤΤ με είσοδο x=1/s βηματική για να πάρεις μόνιμο σφάλμα θέσης
προσθέτεις και από ΘΤΤ της διαταραχής
και έχεις e του συστήματος
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 25, 2016, 15:20:16 pm
κομπλε..με γλιτωσες απο τις πραξεις
για το 2ο θεμα τελευταιο ερωτημα εχεις καμια ιδεα;
ειχα βρει μια λυση αλλα δεν ξερω αν ειναι σωστηγια το 2ο θεμα τελευταιο ερωτημα εχεις καμια ιδεα;
παιρνεις Ε(s)=U(s)-Y(s)=U(s)-[U(s)*A(s)+Hyd(s)*d(s)]=U(s)-[U(s)*A(s)+1/(1+A(s))*d(s)]
με d(s)=1/s και U(s)=1/s και επειτα lims->0s*E(s)=απειρο
αλλα με επιφυλαξη δεν ξερω κατα ποσο το απειρο σφαλμα ειναι σωστο αποτελεσμα
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 15:43:18 pm
thanks :)
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Roronoa Zoro on August 25, 2016, 20:41:57 pm
φεβρ09 θεμα 2
τι ελεγκτη βγαλατε στο τελος;
τι ελεγκτη βγαλατε στο τελος;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: georgkonst on August 27, 2016, 12:18:10 pm
το βρηκα η ΧΕ ειναι σωστη απλα ειχα κανει αριθμητικο στην 2βαθμια του Κ
βγαζεις Κ=236,93 και αν πας στην βοηθητικη βγαινει s=+-j5,06
βγαζεις Κ=236,93 και αν πας στην βοηθητικη βγαινει s=+-j5,06
Και εγω με ίδια χαρακτηριστική είμαι αν και δεν μπορώ να βγάλω το κέρδος που λες, μπορείς να ποστάρεις τις πράξεις σου?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 27, 2016, 13:36:27 pm
Και εγω με ίδια χαρακτηριστική είμαι αν και δεν μπορώ να βγάλω το κέρδος που λες, μπορείς να ποστάρεις τις πράξεις σου?
στην 4η σειρα του πινακα Routh βγαζεις την εξισωση (1416-Κ)*(199+Κ)/17 -17*(120+7Κ)=0και προκυπτει η 2βαθμια -Κ2 -806Κ +247104=0
αν την λυσεις θα βγαλεις 2 λυσεις για το Κ το 236,93 και το -1042,93.
παιρνεις την τιμη 236,93 πας στην βοηθητικη του πινακα Routh(με το s2)
και εχεις ((1416-Κ)/17)s2 +120+7K=0 απο τη οποια βγαινει τελικα το
ζητουμενο s=+-j5,06
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: georgkonst on August 27, 2016, 14:27:52 pm
στην 4η σειρα του πινακα Routh βγαζεις την εξισωση (1416-Κ)*(199+Κ)/17 -17*(120+7Κ)=0
και προκυπτει η 2βαθμια -Κ2 -806Κ +247104=0
αν την λυσεις θα βγαλεις 2 λυσεις για το Κ το 236,93 και το -1042,93.
παιρνεις την τιμη 236,93 πας στην βοηθητικη του πινακα Routh(με το s2)
και εχεις ((1416-Κ)/17)s2 +120+7K=0 απο τη οποια βγαινει τελικα το
ζητουμενο s=+-j5,06
Σωστό χαζά λάθη στις πράξεις, ευχαριστώκαι προκυπτει η 2βαθμια -Κ2 -806Κ +247104=0
αν την λυσεις θα βγαλεις 2 λυσεις για το Κ το 236,93 και το -1042,93.
παιρνεις την τιμη 236,93 πας στην βοηθητικη του πινακα Routh(με το s2)
και εχεις ((1416-Κ)/17)s2 +120+7K=0 απο τη οποια βγαινει τελικα το
ζητουμενο s=+-j5,06
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 27, 2016, 15:00:02 pm
Σωστό χαζά λάθη στις πράξεις, ευχαριστώ
;)Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: geralt on August 27, 2016, 20:09:35 pm
Ο συλογισμος ρε παιδια δεν ειναι λιγο πιο απλος απο οτι το παιδευετε; Ξεκαθαρα το ω_c<=ω_b αρα αν πχ ω_b>50 r/s then λεω εστω ω_c=ω_b>50 r/s αρα και ω_c>50r/s και προχωρω ετσι. Οχι;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 01:20:06 am
Έχει κανείς καμιά ιδέα για το γ) ερώτημα στο θέμα 1 Ιουνίου 2016??Ναι,είδα ότι έγινε ερώτηση και σε προηγούμενες σελίδες,αλλά δε βρήκα καμιά απάντηση....
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Aprosklitos on August 28, 2016, 10:26:31 am
Έχει κανείς καμιά ιδέα για το γ) ερώτημα στο θέμα 1 Ιουνίου 2016??Ναι,είδα ότι έγινε ερώτηση και σε προηγούμενες σελίδες,αλλά δε βρήκα καμιά απάντηση....
ωc*T<θm
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 13:39:51 pm
λυσεις φεβρουαριου 2010 θεμα 1 σελιδα 52
Σελίδα 52??Εννοείς στο τόπικ??Δεν υπάρχει κάτι τέτοιο στη σελίδα 52....
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 13:43:10 pm
Σελίδα 52??Εννοείς στο τόπικ??Δεν υπάρχει κάτι τέτοιο στη σελίδα 52....
λυσεις φεβρουαριου 2010 θεμα 1 σελιδα 53,στο τοπικ ναιTitle: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 13:45:17 pm
λυσεις φεβρουαριου 2010 θεμα 1 σελιδα 53,στο τοπικ ναι
Ναι,το βρήκα,αλλά μάλλον έχουν αφαιρεθεί τα αρχεία γιατί δεν μπορώ να ανοίξω κανένα από αυτά...
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 13:56:58 pm
Ναι,το βρήκα,αλλά μάλλον έχουν αφαιρεθεί τα αρχεία γιατί δεν μπορώ να ανοίξω κανένα από αυτά...
ποιος τα αφαιρεσε??Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 13:59:26 pm
ποιος τα αφαιρεσε??
Δεν ξέρω,αυτό μου έβγαζε σαν μήνυμα όταν πήγαινα να τα ανοίξω,και τα pdf και τις φωτογραφίες.
Ευχαριστώ πολύ πάντως!!!! :)
Κι αφού έχεις κι άλλα όπως βλέπω,ανέβασέ τα,μην ντρέπεσαι!!! :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 14:02:38 pm
Δεν ξέρω,αυτό μου έβγαζε σαν μήνυμα όταν πήγαινα να τα ανοίξω,και τα pdf και τις φωτογραφίες.
Ευχαριστώ πολύ πάντως!!!! :)
Κι αφού έχεις κι άλλα όπως βλέπω,ανέβασέ τα,μην ντρέπεσαι!!! :D
Ευχαριστώ πολύ πάντως!!!! :)
Κι αφού έχεις κι άλλα όπως βλέπω,ανέβασέ τα,μην ντρέπεσαι!!! :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 14:04:36 pm
Ήλπιζα σε λύσεις,αλλά thanks anyway!!!!
Υ.Γ. Αυτά υπάρχουν και στα downloads,έτσι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 14:07:58 pm
Δεν ξέρω,αυτό μου έβγαζε σαν μήνυμα όταν πήγαινα να τα ανοίξω,και τα pdf και τις φωτογραφίες.
Ευχαριστώ πολύ πάντως!!!! :)
Κι αφού έχεις κι άλλα όπως βλέπω,ανέβασέ τα,μην ντρέπεσαι!!! :D
Ευχαριστώ πολύ πάντως!!!! :)
Κι αφού έχεις κι άλλα όπως βλέπω,ανέβασέ τα,μην ντρέπεσαι!!! :D
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 14:13:35 pm
Ήλπιζα σε λύσεις,αλλά thanks anyway!!!!
Υ.Γ. Αυτά υπάρχουν και στα downloads,έτσι?
ναι αλλα αποτι διαβασα στο τοπικ κατεβηκαν και απο κει για καποιο λογο..Υ.Γ. Αυτά υπάρχουν και στα downloads,έτσι?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: JakeLaMotta on August 28, 2016, 14:26:46 pm
Είσαι ωραίος!!!!
Νομίζω ότι λειτουργούν κανονικά τώρα τα downloads πάντως,αλλά βλέπω έχεις και κάποια παραπάνω εδώ!!
Νομίζω ότι λειτουργούν κανονικά τώρα τα downloads πάντως,αλλά βλέπω έχεις και κάποια παραπάνω εδώ!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on August 28, 2016, 14:38:05 pm
Είσαι ωραίος!!!!
Νομίζω ότι λειτουργούν κανονικά τώρα τα downloads πάντως,αλλά βλέπω έχεις και κάποια παραπάνω εδώ!!
τιποτα συναδελεφε!! :)Νομίζω ότι λειτουργούν κανονικά τώρα τα downloads πάντως,αλλά βλέπω έχεις και κάποια παραπάνω εδώ!!
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Niobe on January 30, 2017, 19:37:16 pm
Στη συλλογη θεματων 2011 με 2014, στο θεμα 2 Σεπτεμβρη του 12 (σελ. 10 του pdf) νομιζω υπαρχει αριθμητικο λαθος στο κριτηριο routh, μπορει καποιος να το επιβεβαιωσει;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on January 30, 2017, 20:27:56 pm
εκτος απο τον ιουνιο 2016 ειναι και τα θεματα του φλεβαρη,σεπτεμβρη 2009
που συναντας 4ου και 5ου βαθμου εξισωσεις και πρεπει να τις λυσεις για να βρεις
τα σημεια αποσχισης για τον ΓΤΡ.. δεν μπορω να βρω καποιο τρικ για να λυθουν
που συναντας 4ου και 5ου βαθμου εξισωσεις και πρεπει να τις λυσεις για να βρεις
τα σημεια αποσχισης για τον ΓΤΡ.. δεν μπορω να βρω καποιο τρικ για να λυθουν
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on January 30, 2017, 20:29:13 pm
Στη συλλογη θεματων 2011 με 2014, στο θεμα 2 Σεπτεμβρη του 12 (σελ. 10 του pdf) νομιζω υπαρχει αριθμητικο λαθος στο κριτηριο routh, μπορει καποιος να το επιβεβαιωσει;
γενικα υπαρχουν λαθη σε αυτα τα λυμενα πολυ πιθανον να εχει καποιο λαθος και σε αυτο που αναφερεις.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Niobe on January 30, 2017, 21:12:49 pm
γενικα υπαρχουν λαθη σε αυτα τα λυμενα πολυ πιθανον να εχει καποιο λαθος και σε αυτο
που αναφερεις.
που αναφερεις.
Κουλ.
Επισης εχει κανεις τις εκφωνησεις ιανουαριου του '13;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: hetfield on January 30, 2017, 21:16:29 pm
Κουλ.
Επισης εχει κανεις τις εκφωνησεις ιανουαριου του '13;
Επισης εχει κανεις τις εκφωνησεις ιανουαριου του '13;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: menelaos619 on January 31, 2017, 15:43:06 pm
Στο θέμα 1 του Ιανουαρίου 2011 πως προκύπτει περιθωριο κερδους gm*K=8?Περιθωριο κερδους στο βιβλιο λεει βρισκουμε η απο bode η απο nyquist!?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: ANDREAMK on January 31, 2017, 16:37:36 pm
Στο θέμα 1 του Ιανουαρίου 2011 πως προκύπτει περιθωριο κερδους gm*K=8?Περιθωριο κερδους στο βιβλιο λεει βρισκουμε η απο bode η απο nyquist!?
gm=k0/k οπου k0 είναι η οριακή τιμή που χάνεται η ευστάθεια και βρίσκουμε μεσω Routh και είναι και αυτός ένος τρόπος υπολογισμού του περιθωριου κέρδους αν έχουμε ανισότητα για gm. Κάτι τέτοιο έχω καταλάβει. Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: menelaos619 on January 31, 2017, 17:01:44 pm
gm=k0/k οπου k0 είναι η οριακή τιμή που χάνεται η ευστάθεια και βρίσκουμε μεσω Routh και είναι και αυτός ένος τρόπος υπολογισμού του περιθωριου κέρδους αν έχουμε ανισότητα για gm. Κάτι τέτοιο έχω καταλάβει.
Σε ευχαριστώ πολυ φίλε
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: κύριος Φασόλης on August 23, 2017, 13:38:36 pm
απο το θεμα 2 Σεπτ12 εκει που ζηταει περιθωριο κερδους γενικα η μεθοδολογια ειναι: κανω Routh στη χαρακτηριστικη και για το κ για το οποιο βρω οτι χανεται η ευσταθια αυτο ειναι και το περιθωριο κερδους μου;
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: τεκίλα_αλάτι_λεμόνι on January 27, 2018, 19:35:08 pm
παιδιά έχει λύσει κάποιος το δεύτερο θέμα του Ιανουαρλιου 2011, και αν ναι να δώσει μια εξήγηση?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: MrRobot on January 27, 2018, 19:55:32 pm
Δες από εδώ (https://www.thmmy.gr/smf/index.php?topic=1919.msg935067#msg935067) και κάτω. Έχει ξαναγίνει αυτή η ερώτηση χρόνια πριν. Έχει και στην επόμενη σελίδα κάποια πράγματα.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: τεκίλα_αλάτι_λεμόνι on January 27, 2018, 23:55:05 pm
Δες από εδώ (https://www.thmmy.gr/smf/index.php?topic=1919.msg935067#msg935067) και κάτω. Έχει ξαναγίνει αυτή η ερώτηση χρόνια πριν. Έχει και στην επόμενη σελίδα κάποια πράγματα.
Ευχαριστώ πολύ.. Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Niobe on January 28, 2018, 19:55:28 pm
Στο θέμα 1, Σεπτέμβρης '12 ερώτημα β, στο pdf των λύσεων γράφει για το εύρος ζώνης πως 20log(|H(jωb)|)=17
Αυτό θεωρείται γνωστός τύπος? Αν όχι από που προκύπτει?
Αυτό θεωρείται γνωστός τύπος? Αν όχι από που προκύπτει?
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: greekoo on January 28, 2018, 21:08:23 pm
Στο θέμα 1, Σεπτέμβρης '12 ερώτημα β, στο pdf των λύσεων γράφει για το εύρος ζώνης πως 20log(|H(jωb)|)=17
Αυτό θεωρείται γνωστός τύπος? Αν όχι από που προκύπτει?
Αυτό θεωρείται γνωστός τύπος? Αν όχι από που προκύπτει?
Νομιζω προκύπτει απ'το γεγονός οτι ευρος ζωνης είναι εκεί που παρατηρείς μείωση κατα 3 dB απτο κέρδος. Αρα αν το αρχικός σ κέρδος είναι 20 τότε μείωση -3 θα σ παει στο 17, κ Έτσι προκύπτει.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: leukosaraphs! on August 04, 2018, 13:51:34 pm
Επειδή το topic ήταν χαώδες, 70+ σελίδες, γίνεται μια προσπάθεια να χωριστούν τα θέματα σ' ένα νέο board (https://www.thmmy.gr/smf/index.php?board=575.0) με βάση την χρονιά εξέτασης. Προς το παρόν, δεν έχουν γίνει όλες οι χρονιές, αλλά για όσες υπάρχουν να γράφετε σε εκείνα τα topics, ώστε να υπάρχει μια οργάνωση στις απορίες αλλά και στα λυμένα που ανεβαίνουν.
Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Σουλης on January 23, 2019, 23:44:20 pm
τα ποστς με καινουριες αποριες εγιναν merge στο αντιστοιχο τους board. Λιγη προσοχη απο δω και περα να γραφουμε τις αποριες μας στο τοπικ της καταλληλης χρονιας
Title: Re: [ΣΑΕ Ι] Παλιά θέματα
Post by: Μπιγκόνια on September 17, 2019, 13:53:34 pm
Επειδή το topic ήταν χαώδες, 70+ σελίδες, γίνεται μια προσπάθεια να χωριστούν τα θέματα σ' ένα νέο board (https://www.thmmy.gr/smf/index.php?board=575.0) με βάση την χρονιά εξέτασης. Προς το παρόν, δεν έχουν γίνει όλες οι χρονιές, αλλά για όσες υπάρχουν να γράφετε σε εκείνα τα topics, ώστε να υπάρχει μια οργάνωση στις απορίες αλλά και στα λυμένα που ανεβαίνουν.
Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
Δεν γράφουμε εδώ για θέματα πριν το 2022 γιατί έχουμε νέο board (https://www.thmmy.gr/smf/index.php?board=575.0) Υγ. Αν βρείτε κάποια απάντηση σε λάθος χρονιά, κάντε ένα report -με αιτιολόγηση- για να μεταφερθεί,εκ νέου, στο σωστό topic.
edit: year