Title: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: dim on July 02, 2005, 00:27:21 am
Εδώ μπορείτε να σχολιάζετε τα θέματα και
να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού ΙΙ.
(Τα παλιά θέματα υπάρχουν στον τομέα Downloads)
να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού ΙΙ.
(Τα παλιά θέματα υπάρχουν στον τομέα Downloads)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: beil on August 21, 2006, 14:37:23 pm
Επείδη τα παλιά θέματα που είναι ανεβασμένα είναι "ληγμένα" (το ποιό πρόσφατο είναι Σεπτέμβριος 2001).. :(
θερμή παράκληση: όποιος έχει ποιό πρόσφατα θέματα, please να τα ανεβάσει...
θερμή παράκληση: όποιος έχει ποιό πρόσφατα θέματα, please να τα ανεβάσει...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alexkasgr on August 21, 2006, 14:51:03 pm
Επείδη τα παλιά θέματα που είναι ανεβασμένα είναι "ληγμένα" (το ποιό πρόσφατο είναι Σεπτέμβριος 2001).. :(
θερμή παράκληση: όποιος έχει ποιό πρόσφατα θέματα, please να τα ανεβάσει...
θερμή παράκληση: όποιος έχει ποιό πρόσφατα θέματα, please να τα ανεβάσει...
Νομίζω ότι τα θέματα επαναλαμβάνονται, άρα δεν έχει σημασία πόσο παλιά είναι.
Ό,τι υπάρχει βέβαια (αν υπάρχει) καλό είναι να ανέβει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnny_d on September 29, 2006, 02:15:08 am
Ρε παιδιά,
Εχει κρατήσει κανείς τα θέματα της 1ης εξεταστικής???
Αν τα έχει κρατήσει κανείς ας τα ανεβάσει....
Ήταν λίγο περίεργα σε σχέση με οτι βάζουν συνήθως.... :(
Το 1ο θέμα με την γραμμική προσέγγιση πώς έβγαινε?? :???: :???:
Εχει κρατήσει κανείς τα θέματα της 1ης εξεταστικής???
Αν τα έχει κρατήσει κανείς ας τα ανεβάσει....
Ήταν λίγο περίεργα σε σχέση με οτι βάζουν συνήθως.... :(
Το 1ο θέμα με την γραμμική προσέγγιση πώς έβγαινε?? :???: :???:
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: (Stalin)^2 on September 29, 2006, 02:40:44 am
Το πρώτο φίλε μου ήταν μια ηλιθιότητα σίγουρα εμπνευσμένη απ' την Κωνσταντινίδου...
Έναν τύπο έπερε να θυμάσαι, την συνάρτηση γραμμικής προσέγγισης της συνάρτησης f για το δοθέν σημείο (x0,y0):
g(x,y)=fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0), όπου fx, fy οι μερικές παράγωγοι της f ως προς x και y...
Έκανες αντικατάσταση το σημείο και αυτό ήτανε... 1 μονάδα δώρο...την οποία έχασα... >:(
έδιτ: έλενξέ το, μπορέι να κάνω κάποιο λάθος, δεν έχω το βιβλίο μπροστά μου. Κοίτα στο ολικό διαφορικό.
Έναν τύπο έπερε να θυμάσαι, την συνάρτηση γραμμικής προσέγγισης της συνάρτησης f για το δοθέν σημείο (x0,y0):
g(x,y)=fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0), όπου fx, fy οι μερικές παράγωγοι της f ως προς x και y...
Έκανες αντικατάσταση το σημείο και αυτό ήτανε... 1 μονάδα δώρο...την οποία έχασα... >:(
έδιτ: έλενξέ το, μπορέι να κάνω κάποιο λάθος, δεν έχω το βιβλίο μπροστά μου. Κοίτα στο ολικό διαφορικό.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnny_d on September 29, 2006, 02:49:40 am
K εγω το έχασα ρε γαμωτο....
4 πήρα.... >:( >:(
Στο βιβλίο υπαρχει πουθενά αυτο???
4 πήρα.... >:( >:(
Στο βιβλίο υπαρχει πουθενά αυτο???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: asousos on September 29, 2006, 04:55:23 am
"ΛΟΓΙΣΜΟΣ ΣΥΝΑΡΤΗΣΕΩΝ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ" ΣΕΛ 142 (κάτω-κάτω)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: asousos on September 29, 2006, 05:10:48 am
Γενικότερα τα θέματα που μπήκαν ήταν:
1)γραμμική προσέγγιση
2)πεπελεγμένες συναρτήσεις(καλά τις ασκήσεις του βιβλίου, από εκεί μπήκε η άσκηση)
3)διπλό ολοκλήρωμα
4)τριπλό ολοκλήρωμα (αντικατάσταη κυλινδρικών με σφαιρικών συντεταγμένων)
5)διανυσματικά πεδία (πεδίο αστρόβιλο? ποια η συναρτηση δυναμικού? ποια η δυναμική ενέργεια?)
6)φυσική παραμέτρηση καμπύλης, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα
7)εξίσωση επιφάνειας που βρίσκεται σε παραμετρική μορφή...
αυτά πάνω-κάτω...
1)γραμμική προσέγγιση
2)πεπελεγμένες συναρτήσεις(καλά τις ασκήσεις του βιβλίου, από εκεί μπήκε η άσκηση)
3)διπλό ολοκλήρωμα
4)τριπλό ολοκλήρωμα (αντικατάσταη κυλινδρικών με σφαιρικών συντεταγμένων)
5)διανυσματικά πεδία (πεδίο αστρόβιλο? ποια η συναρτηση δυναμικού? ποια η δυναμική ενέργεια?)
6)φυσική παραμέτρηση καμπύλης, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα
7)εξίσωση επιφάνειας που βρίσκεται σε παραμετρική μορφή...
αυτά πάνω-κάτω...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Krono on September 29, 2006, 10:42:50 am
την συνάρτηση γραμμικής προσέγγισης της συνάρτησης f για το δοθέν σημείο (x0,y0):
g(x,y)=fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0), όπου fx, fy οι μερικές παράγωγοι της f ως προς x και y...
g(x,y)=fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0), όπου fx, fy οι μερικές παράγωγοι της f ως προς x και y...
Ο σωστός τύπος είναι:
g(x,y)=f(x0,y0)+fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: (Stalin)^2 on September 29, 2006, 11:46:47 am
Ναι μπράβο αυτό είναι...
Σόρυ για την παραπληροφόρηση... :-\
Σόρυ για την παραπληροφόρηση... :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnny_d on October 01, 2006, 05:21:48 am
Ξερει κανείς πως βγαίνανε αυτα τα θέματα με την αλλαγή μεταβλητών στα ολοκληρώματα???
:-\ :-\ :-\ :-\ :-\
:-\ :-\ :-\ :-\ :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on October 01, 2006, 09:16:20 am
Θυμάσαι ακριβώς πως ήτανε;
Γενικά πρέπει να κάνεις το σχήμα για να βρεις τον τόπο ολοκλήρωσης, ειδικά όταν κάνεις μετασχηματισμό σε πολικές, κυλινδρικές ή σφαιρικές συντεταγμένες
Γενικά πρέπει να κάνεις το σχήμα για να βρεις τον τόπο ολοκλήρωσης, ειδικά όταν κάνεις μετασχηματισμό σε πολικές, κυλινδρικές ή σφαιρικές συντεταγμένες
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnny_d on October 01, 2006, 15:20:41 pm
Νομίζω οτι ήθελε μετασχηματισμό απο πολικές σε καρτεσιανές... το ενα
και απο σφαιρικές σε κυλινδρικές το άλλο.... :???:
Εγώ τότε είχα κάνει σχήμα και είχα βγάλει τα όρια από τις σχέσεις μετασχηματισμού....
Αλλά δεν πέρασα.... :D :D
Αν ξέρει κάποιος στα σίγουρα ας με διαφωτίσει!!! ;)
και απο σφαιρικές σε κυλινδρικές το άλλο.... :???:
Εγώ τότε είχα κάνει σχήμα και είχα βγάλει τα όρια από τις σχέσεις μετασχηματισμού....
Αλλά δεν πέρασα.... :D :D
Αν ξέρει κάποιος στα σίγουρα ας με διαφωτίσει!!! ;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Schumacher on October 01, 2006, 19:50:51 pm
Συνάδελφοι στα θέματα σεπτεμβρίου θυμάμαι ένα θέμα που είχε πέσει αλλά δεν κατάφερα να το λύσω.Θα ήθελα να με βοηθήσει κάποιος με τη λύση του.
Δείξτε ότι το διανυσμάτικο πεδίο στο επίπεδο F= (2x+ψ)*ι +(6x+ψ)*j είναι συντηριτικό και κάνοντας χρήση του θεωρήματος του Green βρέστε το δυναμικό του.
Ευχαριστώ προκαταβολικά.
Δείξτε ότι το διανυσμάτικο πεδίο στο επίπεδο F= (2x+ψ)*ι +(6x+ψ)*j είναι συντηριτικό και κάνοντας χρήση του θεωρήματος του Green βρέστε το δυναμικό του.
Ευχαριστώ προκαταβολικά.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on October 01, 2006, 20:58:41 pm
Σίγουρα είναι αυτό το πεδίο; Αυτό δεν είναι συντηρητικό αφού θQ/θx = 6 και θP/θy = 1
Πάντως το θυμάμαι αυτό το θέμα. Ήταν πολύ παράξενο, γιατί ζητούσε εφαρμογή του τύπου του Green με έναν περίεργο τρόπο. Έπρεπε να δεχτείς ότι το δυναμικό ισούται με το ολοκλήρωμα πάνω σε μια καμπύλη και στη συνέχεια να δείξεις ότι είναι ανεξάρτητο της καμπύλης που επιλέγεις :-/.
Τουλάχιστον εγώ αυτό έκανα: Το δυναμικό στο τυχαίο σημείο Μ είναι ίσο με το επικαμπύλιο ολοκλήρωμα Fdr πάνω σε μια τυχαία καμπύλη που συνδέει ένα σημείο που επιλέγεται αυθαίρετα να έχει δυναμικό 0 (επιλέγουμε το Ο(0,0)) με το σημείο Μ. Την ονομάζουμε αυτή c1. Ως c2 παίρνουμε το δρόμο Μ(x0,y0) -> Α(x0,0) -> Ο(0,0) (τεθλασμένη γραμμή). Ο δρόμος c = c1 U c2 είναι μια κλειστή καμπύλη για την οποία θα ισχύει ο τύπος του Green, σύμφωνα με τον οποίο βρίσκουμε ότι το ολοκλήρωμα του Fdr πάνω στη c ισούται με 0. Άρα τα ολοκληρώματα Fdr πάνω στη c1 και c2 θα είναι αντίθετα. Αν πάρουμε το δρόμο c2' Ο(0,0) -> Α(x0,0) -> Μ(x0,y0), τότε το ολοκλήρωμα Fdr σε αυτόν θα είναι αντίθετο με τον c2 άρα ίδιο με το c1. Δείξαμε δηλαδή ότι το ολοκλήρωμα Fdr σε οποιοδήποτε δρόμο (c1) είναι ίσο με το ολοκλήρωμα πάνω στο δρόμο Ο(0,0) -> Α(x0,0) -> Μ(x0,y0). Το ολοκλήρωμα Fdr πάνω στο δρόμο αυτό υπολογίζεται εύκολα αν λάβουμε υπόψιν ότι στο Ο(0,0) -> Α(x0,0) είναι y=0, dy=0 και x από 0 μέχρι x0, ενώ στο Α(x0,0) -> Μ(x0,y0) είναι x=x0 dx=0 και y από 0 μέχρι y0.
(Φυσικά χρησιμοποιούμε ότι $Fdr = $Pdx + $Qdy)
Πάντως το θυμάμαι αυτό το θέμα. Ήταν πολύ παράξενο, γιατί ζητούσε εφαρμογή του τύπου του Green με έναν περίεργο τρόπο. Έπρεπε να δεχτείς ότι το δυναμικό ισούται με το ολοκλήρωμα πάνω σε μια καμπύλη και στη συνέχεια να δείξεις ότι είναι ανεξάρτητο της καμπύλης που επιλέγεις :-/.
Τουλάχιστον εγώ αυτό έκανα: Το δυναμικό στο τυχαίο σημείο Μ είναι ίσο με το επικαμπύλιο ολοκλήρωμα Fdr πάνω σε μια τυχαία καμπύλη που συνδέει ένα σημείο που επιλέγεται αυθαίρετα να έχει δυναμικό 0 (επιλέγουμε το Ο(0,0)) με το σημείο Μ. Την ονομάζουμε αυτή c1. Ως c2 παίρνουμε το δρόμο Μ(x0,y0) -> Α(x0,0) -> Ο(0,0) (τεθλασμένη γραμμή). Ο δρόμος c = c1 U c2 είναι μια κλειστή καμπύλη για την οποία θα ισχύει ο τύπος του Green, σύμφωνα με τον οποίο βρίσκουμε ότι το ολοκλήρωμα του Fdr πάνω στη c ισούται με 0. Άρα τα ολοκληρώματα Fdr πάνω στη c1 και c2 θα είναι αντίθετα. Αν πάρουμε το δρόμο c2' Ο(0,0) -> Α(x0,0) -> Μ(x0,y0), τότε το ολοκλήρωμα Fdr σε αυτόν θα είναι αντίθετο με τον c2 άρα ίδιο με το c1. Δείξαμε δηλαδή ότι το ολοκλήρωμα Fdr σε οποιοδήποτε δρόμο (c1) είναι ίσο με το ολοκλήρωμα πάνω στο δρόμο Ο(0,0) -> Α(x0,0) -> Μ(x0,y0). Το ολοκλήρωμα Fdr πάνω στο δρόμο αυτό υπολογίζεται εύκολα αν λάβουμε υπόψιν ότι στο Ο(0,0) -> Α(x0,0) είναι y=0, dy=0 και x από 0 μέχρι x0, ενώ στο Α(x0,0) -> Μ(x0,y0) είναι x=x0 dx=0 και y από 0 μέχρι y0.
(Φυσικά χρησιμοποιούμε ότι $Fdr = $Pdx + $Qdy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Schumacher on October 02, 2006, 01:16:00 am
Το πεδίο είναι στάνταρ αυτό,κι εγω το παρατήρησα ότι το πεδίο δεν είναι συντηρητικό,επίσης παρατήρησα στην εκφώνηση οτι δε λέει το διανυσματικό επίπεδο ειναι F=(2χ+ψ)*ι+ (6x+ψ)*j αλλά στο επίπεδο F=(2χ+ψ)*ι+ (6x+ψ)*j. Μήπως αυτό έχει κάποια διαφορά;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on October 02, 2006, 10:35:49 am
Εγώ που είχα λογικά θέματα της άλλης ομάδας έλεγε το ίδιο πράγμα και νομίζω ότι εννοεί ότι το διανυσματικό πεδίο αυτό είναι πάνω στο επίπεδο, δηλαδή στο xOy. Δεν έχει νόημα η άλλη εξήγηση (δηλαδή ότι η εξίσωση F δίνει το επίπεδο για δύο λόγους:
1) Η τρίτη συνίστώσα είναι 0, άρα το επίπεδο είναι και πάλι το xOy
2) Ποιο είναι το διανυσματικό πεδίο τότε;
Στο δικό μας έβγαινε κανονικά συντηρητικό. Και από κανέναν άλλο δεν άκουσα ότι το πεδίο δεν έβγαινε συντηρητικό. Θα είχε γίνει θέμα...
Το συζήτησες εσύ με κανέναν άλλο;
1) Η τρίτη συνίστώσα είναι 0, άρα το επίπεδο είναι και πάλι το xOy
2) Ποιο είναι το διανυσματικό πεδίο τότε;
Στο δικό μας έβγαινε κανονικά συντηρητικό. Και από κανέναν άλλο δεν άκουσα ότι το πεδίο δεν έβγαινε συντηρητικό. Θα είχε γίνει θέμα...
Το συζήτησες εσύ με κανέναν άλλο;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: spartangr01 on October 02, 2006, 19:17:12 pm
Γενικότερα τα θέματα που μπήκαν ήταν:
1)γραμμική προσέγγιση
2)πεπελεγμένες συναρτήσεις(καλά τις ασκήσεις του βιβλίου, από εκεί μπήκε η άσκηση)
3)διπλό ολοκλήρωμα
4)τριπλό ολοκλήρωμα (αντικατάσταη κυλινδρικών με σφαιρικών συντεταγμένων)
5)διανυσματικά πεδία (πεδίο αστρόβιλο? ποια η συναρτηση δυναμικού? ποια η δυναμική ενέργεια?)
6)φυσική παραμέτρηση καμπύλης, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα
7)εξίσωση επιφάνειας που βρίσκεται σε παραμετρική μορφή...
αυτά πάνω-κάτω...
ΜΗΠΩΣ ΜΠΟΡΕΙΣ ΝΑ ΕΙΣΑΙ ΛΙΓΟ ΠΙΟ ΣΥΓΚΕΚΡΙΜΕΝΟΣ
ΑΣ ΠΟΥΜΕ ΣΤΙΣ ΠΕΠΛΕΓΜΕΝΕΣ ΕΒΑΛΕ ΣΥΣΤΗΜΑ ΕΞΙΣΩΣΕΩΝ??
ΕΥΧΑΡΙΣΤΩ
1)γραμμική προσέγγιση
2)πεπελεγμένες συναρτήσεις(καλά τις ασκήσεις του βιβλίου, από εκεί μπήκε η άσκηση)
3)διπλό ολοκλήρωμα
4)τριπλό ολοκλήρωμα (αντικατάσταη κυλινδρικών με σφαιρικών συντεταγμένων)
5)διανυσματικά πεδία (πεδίο αστρόβιλο? ποια η συναρτηση δυναμικού? ποια η δυναμική ενέργεια?)
6)φυσική παραμέτρηση καμπύλης, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα
7)εξίσωση επιφάνειας που βρίσκεται σε παραμετρική μορφή...
αυτά πάνω-κάτω...
ΜΗΠΩΣ ΜΠΟΡΕΙΣ ΝΑ ΕΙΣΑΙ ΛΙΓΟ ΠΙΟ ΣΥΓΚΕΚΡΙΜΕΝΟΣ
ΑΣ ΠΟΥΜΕ ΣΤΙΣ ΠΕΠΛΕΓΜΕΝΕΣ ΕΒΑΛΕ ΣΥΣΤΗΜΑ ΕΞΙΣΩΣΕΩΝ??
ΕΥΧΑΡΙΣΤΩ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: asousos on October 03, 2006, 03:53:02 am
Sorry για την καθυστέρηση... Δεν ξέρω κατά πόσο βοηθάω τέτοια ώρα, αλλά τώρα είδα το post...
Quote
1)γραμμική προσέγγιση
...normal...Quote
2)πεπελεγμένες συναρτήσεις(καλά τις ασκήσεις του βιβλίου, από εκεί μπήκε η άσκηση)
...συγκεκριμένα μπήκε η άσκηση 24,σελ 275... τέτοιο στυλ.Quote
3)διπλό ολοκλήρωμα
...μετασχηματισμός σε πολικές συντεταγμένες...Quote
4)τριπλό ολοκλήρωμα (αντικατάσταη κυλινδρικών με σφαιρικών συντεταγμένων)
...άσκηση 13 βιβλίου,σελ 460...Quote
5)διανυσματικά πεδία (πεδίο αστρόβιλο? ποια η συναρτηση δυναμικού? ποια η δυναμική ενέργεια?)
...άσκηση 28,σελ 179...(+ποια είναι η δυναμική ενέργεια...)Quote
6)φυσική παραμέτρηση καμπύλης, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα
...normal...Quote
7)εξίσωση επιφάνειας που βρίσκεται σε παραμετρική μορφή...
...περίπου: άσκηση 2,σελ. 408... (+ν.δ.ο. είναι λεία)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TeeKay on September 18, 2007, 13:22:14 pm
Πώς σας φάνηκαν τα σημερινά θέματα; ::)
Εγώ έχω την εξής απορία: το γεγονός ότι μπορούσαμε να συγκεντρώσουμε μέχρι 11 μονάδες σημαίνει ότι αν π.χ. γράψαμε 5 αυτός ο βαθμός θα διαιρεθεί με 1.1 (=4.54); Η θα παραμείνει 5;
Εγώ έχω την εξής απορία: το γεγονός ότι μπορούσαμε να συγκεντρώσουμε μέχρι 11 μονάδες σημαίνει ότι αν π.χ. γράψαμε 5 αυτός ο βαθμός θα διαιρεθεί με 1.1 (=4.54); Η θα παραμείνει 5;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasso on September 18, 2007, 22:29:20 pm
Το άριστα είναι πάλι το 10. Η 11η μονάδα είναι βοηθητική..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on March 27, 2008, 17:04:56 pm
Μια ερώτηση, για όσους έδωσαν πέρισυ....
Η φιλοσοφια των θεμάτων καλύπτεται από το βιβλίο γενικά? Ή υπάρχουν σειρές ασκήσεων που γίνονται στο μάθημα και δεν τις καλύπτει το βιβλίο? κοινώς δλδ, άμα διαβάσεις τις ασκήσεις του βιβλίου περνάς ή όχι?
Η φιλοσοφια των θεμάτων καλύπτεται από το βιβλίο γενικά? Ή υπάρχουν σειρές ασκήσεων που γίνονται στο μάθημα και δεν τις καλύπτει το βιβλίο? κοινώς δλδ, άμα διαβάσεις τις ασκήσεις του βιβλίου περνάς ή όχι?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Godhatesusall on March 27, 2008, 17:15:00 pm
Μια ερώτηση, για όσους έδωσαν πέρισυ....
Η φιλοσοφια των θεμάτων καλύπτεται από το βιβλίο γενικά? Ή υπάρχουν σειρές ασκήσεων που γίνονται στο μάθημα και δεν τις καλύπτει το βιβλίο? κοινώς δλδ, άμα διαβάσεις τις ασκήσεις του βιβλίου περνάς ή όχι?
Η φιλοσοφια των θεμάτων καλύπτεται από το βιβλίο γενικά? Ή υπάρχουν σειρές ασκήσεων που γίνονται στο μάθημα και δεν τις καλύπτει το βιβλίο? κοινώς δλδ, άμα διαβάσεις τις ασκήσεις του βιβλίου περνάς ή όχι?
Τα της κωνσταντινίδου(το πορτοκαλί βιβλίο) τα περνάς με άνεση αν έχεις διαβάσει πλήρως ότι λέει το βιβλίο,αφού βάζει παρόμοια θέματα με αυτά του βιβλίου.Όσο για τον κάππο θα βάλει θέματα λίγο πιο δύσκολα,που χρειάζονται παραπάνω σκέψη,αλλά και κανά θέμα πιο βατό.Συνολικά πιστεύω ότι αν έχεις διαβάσει ΟΛΗ την ύλη μαζί με λυμένα παραδείγματα,και έχεις λύσει λίγες ασκήσεις από κάθε κεφάλαιο τότε το 7 το έχεις άνετα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Wade on March 27, 2008, 21:59:57 pm
Όντως, στο κομμάτι της κ. Κωνσταντινίδου, τα θέματα που βάζει μοιάζουν αρκετά με τα λυμένα παραδείγματα του βιβλίου, και η θεωρία του βιβλίου πιστεύω καλύπτει πολύ καλά τα όσα χρειάζονται για τις εξετάσεις. Ο κ. Κάππος πέρσι είχε βάλει "έξυπνα" θέματα, που όμως έβγαιναν με λίγη σκέψη. Θέματα παρόμοια με αυτά που βάζει ο κ. Κάππος θα έλεγα ότι δεν υπάρχουν στο βιβλίο, γι' αυτό χρειάζεται καλή κατανόηση της θεωρίας. Παρ' όλα αυτά, τα λυμένα παραδείγματα και πάλι βοηθάνε πολύ.
Εκτός βέβαια κι αν άλλαξαν οι διδάσκοντες, οπότε σ' αυτή την περίπτωση τα παραπάνω δεν ισχύουν.
Εκτός βέβαια κι αν άλλαξαν οι διδάσκοντες, οπότε σ' αυτή την περίπτωση τα παραπάνω δεν ισχύουν.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on March 28, 2008, 01:19:58 am
Παιδιά ευχαριστώ για τις απαντήσεις :)
(αν κ δεν ξέρω τι παίζει στην περίπτωση του Ρόθου....)
(αν κ δεν ξέρω τι παίζει στην περίπτωση του Ρόθου....)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Wade on March 28, 2008, 01:38:55 am
Αν κάνει ο κ. Ρόθος, έχω ακούσει ότι είναι πολύ σημαντικές οι σημειώσεις του, επειδή τα θέματά του είναι εμπνευσμένα από αυτές. Άρα, θα μπορούσες να τις βρεις από κάποιον γνωστό σου πρωτοετή ;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on March 28, 2008, 01:55:46 am
Αν κάνει ο κ. Ρόθος, έχω ακούσει ότι είναι πολύ σημαντικές οι σημειώσεις του, επειδή τα θέματά του είναι εμπνευσμένα από αυτές. Άρα, θα μπορούσες να τις βρεις από κάποιον γνωστό σου πρωτοετή ;)
μου είπαν ότι στο ένα τμήμα τουλάχιστον κάνει αυτός.... στο άλλο δεν ξέρω.
Θα το προσπαθήσω... :-\
thanks :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aggalitsas on June 06, 2008, 16:53:16 pm
(http://i18.photobucket.com/albums/b111/fragostafylo/20013.jpg)
πώς λυνεται το πρώτο ερώτημα? :-[
πώς λυνεται το πρώτο ερώτημα? :-[
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aggalitsas on June 06, 2008, 19:04:35 pm
(http://i18.photobucket.com/albums/b111/fragostafylo/20013.jpg)
πώς λυνεται το πρώτο ερώτημα? :-[
το οτι υπάρχει συνάρτηση βγαινει εύκολα ( F(x,y,f(x,y))=0 στο(0,0,0) και Fz!=0 )πώς λυνεται το πρώτο ερώτημα? :-[
και ισχύει Zx=-Fx/Fz kai Zy=-Fy/Fz
πως ομως βρίσκουμε την f?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aggalitsas on June 06, 2008, 19:17:51 pm
τι βλακας που είμαι !! δεν ζητάει την Φ επομένως βγαινει μπαμ μπαμ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasso on June 07, 2008, 22:54:48 pm
προσπαθώντας (μάταια λολ) να λύσω τα παλιά θέματα, βρήκα αρκετά λάθη.. Μπορεί κάποιος να τα επιβεβαιώσει γιατί δεν την πολυπαλεύω εδώ κάτω;
Ιούνιο 91 (Β): όπου fx μπαίνει fu και όπου fv(το δεύτερο) μπαίνει fy
Σεπτέμβρης 95 (Β) 1)το dS μήπως να πάρει δρόμο από το ολοκλήρωμα; (ή κάποια άλλη διόρθωση γιατί βγαίνει dt^2 σε απλό ολοκλήρωμα
5) μήπως εννοεί κάπου z^2?
αν δεν είναι τυπογραφικό, θα ήθελα να μάθω πώς λύνονται.. αν είναι.. πάλι ! ( με εξαίρεση το πρώτο)
Ιούνιο 91 (Β): όπου fx μπαίνει fu και όπου fv(το δεύτερο) μπαίνει fy
Σεπτέμβρης 95 (Β) 1)το dS μήπως να πάρει δρόμο από το ολοκλήρωμα; (ή κάποια άλλη διόρθωση γιατί βγαίνει dt^2 σε απλό ολοκλήρωμα
5) μήπως εννοεί κάπου z^2?
αν δεν είναι τυπογραφικό, θα ήθελα να μάθω πώς λύνονται.. αν είναι.. πάλι ! ( με εξαίρεση το πρώτο)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Laza G on June 08, 2008, 15:03:25 pm
οποιος έχει λύσει τα περσινά θέματα και του 2001 ας με κανει add στο msn να του κάνω κάποιες ερώτησεις...glaza@mail.gr
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Matzika on June 08, 2008, 16:26:31 pm
εχει λύσει κανείς θέματα του Σεπτεμβρίου 2007?θελω να τσεκάρω τροπο λύσης και αποτελέσματα...ας ποστάρει εδώ η ας μ στείλει πμ...
επίσης!Στο 5ο θέμα του 2007 ξέρει κανείς πως γίνεται το σχήμα????? :(
επίσης!Στο 5ο θέμα του 2007 ξέρει κανείς πως γίνεται το σχήμα????? :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on June 08, 2008, 16:35:25 pm
Έχω λύσει το πρώτο θέμα μόνο μέχρι στιγμής (για 2007)
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mysterious on June 08, 2008, 16:44:48 pm
Έχω λύσει το πρώτο θέμα μόνο μέχρι στιγμής (για 2007)
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
Μάλλον λάθος μάθημα.. :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on June 08, 2008, 16:46:50 pm
Μάλλον λάθος μάθημα.. :D
Κι εγώ το κοιτάω κ λέω τι στο καλό... :D
οκ δεν έχω διαβάσει και τρελά, αλλά να μην καταλαβαίνω καν το θέμα ? ! ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: apostolos1986 on June 08, 2008, 18:02:19 pm
εμπλεξε τα σαε 2 ο junior :P :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aggalitsas on June 08, 2008, 18:03:10 pm
στα θεματα σεπτ,2007 ξερει κανεις πως λυνεται το 6?
*παντως πριν καπου ηταν πολυ πιο εύκολα
*παντως πριν καπου ηταν πολυ πιο εύκολα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on June 08, 2008, 19:28:08 pm
Έχω λύσει το πρώτο θέμα μόνο μέχρι στιγμής (για 2007)
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
α) Βρίσκω πίνακα ελεγξιμότητας, έχει ορίζουσα 0, δεν είναι ελέγξιμο.
β) Χρησιμοποιώ πίνακα μετασχηματισμού Ρ, πρώτη στήλη 0,9 και -1,3, δεύτερη στήλη 1 και 0.
γ) Όχι, ο μη ελέγξιμος πόλος είναι ασταθής.
Μάλλον λάθος μάθημα.. :D
Πωωωω δεν πάω καλά!! Με πείραξαν τα ΣΑΕ 2 στο κεφάλι!!
Κατά βάθος θα προτιμούσα να διαβάζω Λογισμό 2, γι' αυτό!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Johnny English on June 08, 2008, 21:06:16 pm
Κατά βάθος θα προτιμούσα να διαβάζω Λογισμό 2, γι' αυτό!
You ARE crazy INDEED!! ^ex_shocked^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasso on June 08, 2008, 21:07:11 pm
Κατά βάθος θα προτιμούσα να διαβάζω Λογισμό 2, γι' αυτό!
You ARE crazy INDEED!! ^ex_shocked^
juan δεν μιλάμε σε άτομα που έγραψαν διψήφιο βαθμό στο λογισμό 2...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on June 08, 2008, 21:17:24 pm
Κατά βάθος θα προτιμούσα να διαβάζω Λογισμό 2, γι' αυτό!
You ARE crazy INDEED!! ^ex_shocked^
+oo
;D
Mexri to septembri h ylh tha xei teleiwsei :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bakeneko on June 08, 2008, 21:47:49 pm
Κατά βάθος θα προτιμούσα να διαβάζω Λογισμό 2, γι' αυτό!
What's wrong with you????!Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Johnny English on June 08, 2008, 21:50:13 pm
juan δεν μιλάμε σε άτομα που έγραψαν διψήφιο βαθμό στο λογισμό 2...
Γιατί ρε?
Χαλαρα τον έχω τον διψήφιο.. ^victory^
1,5...............................................
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on June 08, 2008, 21:52:01 pm
Ααααχχχ τι ωραία που ήταν τότε που διαβάζαμε λογισμό 2... Αλλά όλα τα ωραία κρατάν λίγο... Το πρώτο έτος δεν ξανάρχεται :'(
(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Papatanasis on June 08, 2008, 21:57:33 pm
Ααααχχχ τι ωραία που ήταν τότε που διαβάζαμε λογισμό 2... Αλλά όλα τα ωραία κρατάν λίγο... Το πρώτο έτος δεν ξανάρχεται :'(
(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
Ντροπη ντροπη!(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
Τρομαξα τοσο πολυ που δεν ανοιξα βιβλιο! :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Matzika on June 08, 2008, 22:00:59 pm
Ααααχχχ τι ωραία που ήταν τότε που διαβάζαμε λογισμό 2... Αλλά όλα τα ωραία κρατάν λίγο... Το πρώτο έτος δεν ξανάρχεται :'(
(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
(σκάστε ρε, προσπαθώ να τρομάξω τους νέους)
junior θες να ερθεις να γραψεις για μενα αυριο λογισμό?ετσι για να θυμηθείς τα ωραια χρόνια της νιότης σ και να ξανανιώσεις τις παλιες καλές στιγμές..... ::) ::) ::)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Γιώργος on June 08, 2008, 23:55:05 pm
Χαλαρα τον έχω τον διψήφιο.. ^victory^
Στο δυαδικό; :DΣοζ για το off, καλή επιτυχία! :) :) :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Junior on June 08, 2008, 23:55:36 pm
Για τα μαθηματικά(Το θέμα είναι επίκαιρο):
http://www.thmmy.gr/smf/index.php?topic=23468.msg475516#msg475516
Γιατί άντε!
http://www.thmmy.gr/smf/index.php?topic=23468.msg475516#msg475516
Γιατί άντε!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: apostolos1986 on June 09, 2008, 00:00:18 am
παιδιά θα συμφωνήσω κι εγώ με τον junior... προτιμώ το λογισμό 2 παρά τα σαε... τα οποία τα αντιπαθώ απεριόριστα... :D :D
και φυσικά δεν έχω γράψει διψήφιο 8) 8)
και φυσικά δεν έχω γράψει διψήφιο 8) 8)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasso on June 09, 2008, 14:47:11 pm
για τα σημερινά θέματα..
θα μιλήσω μόνο για Κωνσταντινίδου γιατί μόνο αυτό το κομμάτι ξέρω καλά.
Έβαλε μια χαρά θέματα έχω να πω. Κάποια ερωτήματα πολύ εύκολα, σχεδόν χάριζε τη μιάμιση μονάδα της. Από κει και πέρα, για να πιάσεις 5,5/5,5 έπρεπε να έχεις ξεσκιστεί στο διάβασμα, το 3β) δεν λυνόταν εύκολα.
Διαβαθμισμένα θέματα.. φάιναλι!
για τον Κάππο πείτε άλλοι, αλλά το έχω λίγο παράπονο, δεν έδινε 1μιση μονάδα να περάσεις.. την πρώτη του άσκηση την είχε δώσει μεν στο ιντερνετ, αλλά ήταν κλασσικά μερικά χιλιόμετρα μακριά από τη φιλοσοφία ασκήσεων του βιβλίου...
θα μιλήσω μόνο για Κωνσταντινίδου γιατί μόνο αυτό το κομμάτι ξέρω καλά.
Έβαλε μια χαρά θέματα έχω να πω. Κάποια ερωτήματα πολύ εύκολα, σχεδόν χάριζε τη μιάμιση μονάδα της. Από κει και πέρα, για να πιάσεις 5,5/5,5 έπρεπε να έχεις ξεσκιστεί στο διάβασμα, το 3β) δεν λυνόταν εύκολα.
Διαβαθμισμένα θέματα.. φάιναλι!
για τον Κάππο πείτε άλλοι, αλλά το έχω λίγο παράπονο, δεν έδινε 1μιση μονάδα να περάσεις.. την πρώτη του άσκηση την είχε δώσει μεν στο ιντερνετ, αλλά ήταν κλασσικά μερικά χιλιόμετρα μακριά από τη φιλοσοφία ασκήσεων του βιβλίου...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Airmak_gr on June 09, 2008, 16:16:44 pm
φιλε συμφωνω για κωνστ....δεν πρεπει βεβαια να εγραψα πανω απο 3 σε αυτη...εκει εγραψα.....στον αλλο ομως δεν πρεπει να εχω γραψει 1.5 με τιποτα.......!!!!!!!!αμα ελυνα τον τορο θα περνουσα........Α ΡΕ ΤΟΡΟΣΙΔΗ ΤΙ ΜΑΣ ΕΚΑΝΕΣ!!!!!!!!!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Matzika on June 09, 2008, 17:15:45 pm
Παιδια τι να πω???για μενα η κωνσταντινίδου εβαλε βαρβατα για αυτα που μας εχει συνηθίσει σε αντίθεση με τον Καππο που νομίζω ήταν βατα...
Για να καταλάβετε μ πήρε 1:30 ώρα να λύσω τα θεματα της Κων ( για τα οποία δεν είμαι και πολύ σίγουρη ότι τα έχω σωστά) ενώ για του Καππου 45 λεπτά!! Ενταξει σαφώς δεν θα χαρίσει τη μιαμιση μοναδα...πρέπει να ξερεις και κατι τις από το μπλέ για να το περάσεις το μαθημα...
Τεσπα γενικα αφου εφυγε αυτό έχει σημασία!! :D :D :D
Για να καταλάβετε μ πήρε 1:30 ώρα να λύσω τα θεματα της Κων ( για τα οποία δεν είμαι και πολύ σίγουρη ότι τα έχω σωστά) ενώ για του Καππου 45 λεπτά!! Ενταξει σαφώς δεν θα χαρίσει τη μιαμιση μοναδα...πρέπει να ξερεις και κατι τις από το μπλέ για να το περάσεις το μαθημα...
Τεσπα γενικα αφου εφυγε αυτό έχει σημασία!! :D :D :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: socrates on June 09, 2008, 17:29:53 pm
Εχει καποιος τα θεματα να τα ανεβασει?
Βtw, ειναι απο τα αγαπημενα μου μαθηματα...
Βtw, ειναι απο τα αγαπημενα μου μαθηματα...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: manos88 on June 09, 2008, 18:30:39 pm
Socrates συλλογή θεμάτων κάνεις??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: N3ikoN on August 23, 2008, 01:21:43 am
γειαα!!
από ότι είδα στ downloads δεν έχει προσφατα θέματα.. το κακό είναι ότι δεν πηγαινα κ καθόλου στις παρακολουθήσεις..οπότε δεν έχω ιδεα τι ειδους θεματα πεφτουν στις εξετασεις! αν διαβασω το βιβλιο κ τις σημειωσεις του καππου απο το blackboard ειμαι καλυμμενος? ::)
από ότι είδα στ downloads δεν έχει προσφατα θέματα.. το κακό είναι ότι δεν πηγαινα κ καθόλου στις παρακολουθήσεις..οπότε δεν έχω ιδεα τι ειδους θεματα πεφτουν στις εξετασεις! αν διαβασω το βιβλιο κ τις σημειωσεις του καππου απο το blackboard ειμαι καλυμμενος? ::)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasso on August 23, 2008, 02:52:07 am
ένα 5άρι το πιάνεις..
Κάππο χωρίς σημειώσεις από παρακολουθήσεις Κάππου δεν γράφεις πάνω από 1.5 μονάδα.. Βάζει τα δικά του ιδιαίτερα, μοναδικά θέματα που πρέπει να τον έχεις ζήσει για να τα λύσεις :P
Κάππο χωρίς σημειώσεις από παρακολουθήσεις Κάππου δεν γράφεις πάνω από 1.5 μονάδα.. Βάζει τα δικά του ιδιαίτερα, μοναδικά θέματα που πρέπει να τον έχεις ζήσει για να τα λύσεις :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: N3ikoN on August 23, 2008, 14:09:48 pm
ένα 5άρι το πιάνεις..
Κάππο χωρίς σημειώσεις από παρακολουθήσεις Κάππου δεν γράφεις πάνω από 1.5 μονάδα.. Βάζει τα δικά του ιδιαίτερα, μοναδικά θέματα που πρέπει να τον έχεις ζήσει για να τα λύσεις :P
Κάππο χωρίς σημειώσεις από παρακολουθήσεις Κάππου δεν γράφεις πάνω από 1.5 μονάδα.. Βάζει τα δικά του ιδιαίτερα, μοναδικά θέματα που πρέπει να τον έχεις ζήσει για να τα λύσεις :P
χαχαχαχαχ!! τοσο καλα δλδ :P κατι ειχα ακουσει για τα "ανεπαναληπτα" θεματα του :P ε,οκ, τοτε θα παρω σημειώσεις απο κάποιον φιλο! :P θενκς!
(για να δουμε τι θα δουμε με αυτον τον λογισμο λολ :D)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on September 15, 2008, 12:12:41 pm
Δε μου άρεσαν καθόλου τα θέματα στη σελίδα 2 ^mad^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Emfanever on September 15, 2008, 12:15:13 pm
Δε μου άρεσαν καθόλου τα θέματα στη σελίδα 2 ^mad^
Λογικό!! Εγώ την έκανα από νωρίς με ελαφρά! ^dontknow^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kritikos on September 15, 2008, 12:15:31 pm
πως πήγε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on September 15, 2008, 13:49:28 pm
ας γκρινιαξω κι εγω λιγο
πως πηγε?
οπως θα λεγε και ο χουαν
χαχαχαχα
χαχαχαχαχαχαχαχαχαχα
ΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑ
;D ;D
πως πηγε?
οπως θα λεγε και ο χουαν
χαχαχαχα
χαχαχαχαχαχαχαχαχαχα
ΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑΧΑ
;D ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Godhatesusall on September 15, 2008, 13:51:48 pm
upload τα θέματα asap
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on September 15, 2008, 13:53:40 pm
upload τα θέματα asap
δεν τα χω... αν τα χει κρατησει κανεις ας τα ανεβασει....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: tomshare3 on September 15, 2008, 15:16:53 pm
τα σημερινα θεματα της ομαδας β ειναι στα downloads! ;)
και νομιζα οτι δεν μπορουσε να γινει πιο δυσκολο το μαθημα!! :D :D
και νομιζα οτι δεν μπορουσε να γινει πιο δυσκολο το μαθημα!! :D :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: jiraiya on September 15, 2008, 15:28:58 pm
Εν τω μεταξεί βγαίνει ένας επιτηρητής και λέει στην Κωνσταντινίδου:
"Τα θέματα που έβαλες είναι παιδαριώδη!!"
και αυτή απαντάει
"Συμφωνώ! Στους φοιτητές μου πες το που μου λένε ότι βάζω δύσκολα"!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
"Τα θέματα που έβαλες είναι παιδαριώδη!!"
και αυτή απαντάει
"Συμφωνώ! Στους φοιτητές μου πες το που μου λένε ότι βάζω δύσκολα"!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: gerdi on September 15, 2008, 15:36:28 pm
Άντε καλά ότι να ναι.. Εγώ είχα δώσει και τον Μάιο και πιστεύω ότι ήτανε αρκετά δύσκολα σήμερα. Ητανε πως να το πω....ψαγμένα.....
Απο κει και πέρα το πρόβλημα με το συκγεκριμένο μάθημα δεν είναι η δυσκολία αλλά η ποσότητα της ύλης. Ιδιαίτερα στην ύλη του Κάπου.Δλδ έλεος δεν μπορώ να καταλάβω τον λόγο γτ δεν το σπάνε αυτό το μάθημα????
Έχουμε καταντήσει να παίζουμε τζόγο από τα 10 κεφάλαια διαβάζουμε τα 3 κ όποιος είναι πιο κωλόφαρδος και πέσει θεματάκι απο το κεφάλαιό του περνάει...
(που λέει ο λόγος)
Απο κει και πέρα το πρόβλημα με το συκγεκριμένο μάθημα δεν είναι η δυσκολία αλλά η ποσότητα της ύλης. Ιδιαίτερα στην ύλη του Κάπου.Δλδ έλεος δεν μπορώ να καταλάβω τον λόγο γτ δεν το σπάνε αυτό το μάθημα????
Έχουμε καταντήσει να παίζουμε τζόγο από τα 10 κεφάλαια διαβάζουμε τα 3 κ όποιος είναι πιο κωλόφαρδος και πέσει θεματάκι απο το κεφάλαιό του περνάει...
(που λέει ο λόγος)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Johnny English on September 15, 2008, 15:40:05 pm
Εγώ δήλωσα, την επόμενη φορά που θα δώσω μάθημα Κάππου, αντί για ΤΗΜΜΥ επάνω θα γράψω ΜΙΤ department of mathematics.
Για να ξέρουμε που βρισκόμαστε τελικά..
--
Δε θα γκρινιάξω πολύ, εγώ τα πάλεψα τα θέματα καλούτσικα. Απλώς μια παρατήρηση: Ο σκοπός είναι να μάθουμε μαθηματικά για τα μαθηματικά ή μαθηματικά ως εργαλείο του μηχανικού? Γιατί π.χ. το πλέον σημαντικό θεώρημα GAUSS για τον μηχανικό (Πεδία), βρέθηκε εκτός εξέτασης.. αφήνοντας τη θέση του σε θεωριτικομαθηματικοφιλοσοφίες...
Για να ξέρουμε που βρισκόμαστε τελικά..
--
Δε θα γκρινιάξω πολύ, εγώ τα πάλεψα τα θέματα καλούτσικα. Απλώς μια παρατήρηση: Ο σκοπός είναι να μάθουμε μαθηματικά για τα μαθηματικά ή μαθηματικά ως εργαλείο του μηχανικού? Γιατί π.χ. το πλέον σημαντικό θεώρημα GAUSS για τον μηχανικό (Πεδία), βρέθηκε εκτός εξέτασης.. αφήνοντας τη θέση του σε θεωριτικομαθηματικοφιλοσοφίες...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: jiraiya on September 15, 2008, 16:00:49 pm
Για μένα το μάθημα είναι απίστευτα απαράδεκτο.
Από τη μια σου λένε ότι αυτά που βάζουν είναι μέσα στο βιβλίο ( που ισχύει) αλλά τα βιβλία ειναι 1000 σελίδες.
Η κωνσταντινίδου θέλει να ξέρεις το παραμικρό κομματάκι μέσα στο βιβλίο ( αλλά πάλι καλά που τουλάχιστον είναι εφαρμογές )
και από την άλλη ο Κάπος δε θέλει να ξέρεις τύπους αλλά να έχεις καταλάβει τόσο τη θεωρία ώστε να μπορείς να αποδείξεις
οτιδήποτε αφηρημένο σου δώσει.
Τον Ιούνιο στο ένα θέμα που είχε βάλει με τις καμπύλες, ήθελα να ξεκινήσω την λύση ως εξής:
" Dear Mr Kapos,
I was honoured to have tried to solve....."
Τα θέματά του έχουν καταντήσει έκθεση.
Πραγματικά πιστεύω ότι έχουν τις καλύτερες προθέσεις (ειλικρινά το λέω αυτό!!!), αλλά δεν μπορούν να καταλάβουν το βαθμό δυσκολίας
αυτών που διδάσκουν. Αυτή η ύλη είναι μεγαλύτερη από αυτή των πανελληνίων και απαιτούν να κάνεις αντίστοιχο διάβασμα.
Αυτή είναι η άποψή μου.....
Από τη μια σου λένε ότι αυτά που βάζουν είναι μέσα στο βιβλίο ( που ισχύει) αλλά τα βιβλία ειναι 1000 σελίδες.
Η κωνσταντινίδου θέλει να ξέρεις το παραμικρό κομματάκι μέσα στο βιβλίο ( αλλά πάλι καλά που τουλάχιστον είναι εφαρμογές )
και από την άλλη ο Κάπος δε θέλει να ξέρεις τύπους αλλά να έχεις καταλάβει τόσο τη θεωρία ώστε να μπορείς να αποδείξεις
οτιδήποτε αφηρημένο σου δώσει.
Τον Ιούνιο στο ένα θέμα που είχε βάλει με τις καμπύλες, ήθελα να ξεκινήσω την λύση ως εξής:
" Dear Mr Kapos,
I was honoured to have tried to solve....."
Τα θέματά του έχουν καταντήσει έκθεση.
Πραγματικά πιστεύω ότι έχουν τις καλύτερες προθέσεις (ειλικρινά το λέω αυτό!!!), αλλά δεν μπορούν να καταλάβουν το βαθμό δυσκολίας
αυτών που διδάσκουν. Αυτή η ύλη είναι μεγαλύτερη από αυτή των πανελληνίων και απαιτούν να κάνεις αντίστοιχο διάβασμα.
Αυτή είναι η άποψή μου.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Johnny English on September 15, 2008, 16:06:35 pm
Ναι, να μην παρεξηγηθώ, μπορεί να γκρινιάζω λίγο γενικά για τα πολλά μαθηματικά που κάνουμε.. αλλά κατά βάθος τους χαίρομαι τους μαθηματικούς μας γιατί έχουν μεράκι και το γουστάρουν.. (αυτό είναι και το πρόβλημά μας άλλωστε :P)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pmousoul on September 15, 2008, 16:17:44 pm
Τότε που το έδωσα.. είχε κάνει την πρώτη της εμφάνιση η Ιωαννίδου - δεν ξέρω εάν ήταν το γεγονός ότι δίδασκε για πρώτη φορά, αλλά δεν μου είχε κάνει καθόλου καλή εντύπωση..
Παρόλο που είχε βάλει εύκολα θέματα στον διανυσματικό λογισμό (Gauss, Stokes).. εντούτοις δεν τα έλυσα γιατί ένιωθα μία αποστροφή για αυτό το κομμάτι των μαθηματικών με τον τρόπο που το διδασκόμασταν και το διάβασα αφού πέρασα το μάθημα (πεδιακοί και όχι μόνο λόγοι δηλ.).
Αυτά τα μαθηματικά αποτελούν το Α και το Ω ειδικά των ηλεκτρολόγων μηχανικών, γιατί είναι τα κατεξοχήν χρησιμοποιούμενα στην λύση των προβλημάτων του πεδίου.
Παρόλο που είχε βάλει εύκολα θέματα στον διανυσματικό λογισμό (Gauss, Stokes).. εντούτοις δεν τα έλυσα γιατί ένιωθα μία αποστροφή για αυτό το κομμάτι των μαθηματικών με τον τρόπο που το διδασκόμασταν και το διάβασα αφού πέρασα το μάθημα (πεδιακοί και όχι μόνο λόγοι δηλ.).
Αυτά τα μαθηματικά αποτελούν το Α και το Ω ειδικά των ηλεκτρολόγων μηχανικών, γιατί είναι τα κατεξοχήν χρησιμοποιούμενα στην λύση των προβλημάτων του πεδίου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pmousoul on September 15, 2008, 16:32:33 pm
Επίσης μία συμβουλή για όσους ενδεχομένως θα το ξαναδώσουν (κάτι που δεν το εύχομαι) είναι να διαβάσετε πρώτα τουλάχιστον μία φορά καλά την θεωρία και μετά να δείτε όλα τα παραδείγματα των βιβλίων.
Γιατί και να μην προλάβεις να δεις όλα τα παραδείγματα, εάν έχεις μία ολοκληρωμένη εικόνα του τι παίζει αυτόματα έχεις περισσότερες ευκαιρίες να γράψεις και μάλιστα καλά.
Όλη η θεωρία το Λογισμού ΙΙ είναι 200 το πολύ σελίδες χωρίς τα παραδείγματα..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kafeini on September 15, 2008, 17:59:22 pm
Και εγώ που διάβασα όλα τα παραδείγματα της δ. ανάλυσης τι κατάλαβα; Έγραψα όλα της Κωνσταντινίδου κ από κάππο ούτε 0,5 δεν παίρνω. :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: smo on September 15, 2008, 18:53:31 pm
Εγω παλι για να πω την αληθεια μου φανηκαν τα θεματα αστεια οχι ευκολα αλλα αστεια (ισως ειναι το γελιο του απελπισμενου) παντως ομολογω οτι αν περασω θα το οφειλω στον mr kαππο καθως μονο τα δικα του ελυσα με καποια αξιοπρεπεια και ελαχιστα της κωνσταντινιδου (παρολο που ηταν πιο by the book)
παντως οπως ειπα και διπλα σε κατι τετοια θεματα οπως του καππου καλο θα ηταν να βγαζει κ λυσεις για να ξερουμε και πανω κατω τι ακριβως ζηταει...
παντως οπως ειπα και διπλα σε κατι τετοια θεματα οπως του καππου καλο θα ηταν να βγαζει κ λυσεις για να ξερουμε και πανω κατω τι ακριβως ζηταει...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: N3ikoN on September 15, 2008, 19:36:04 pm
πως πήγε;
τα θεματα τις κωνσταντινιδου ευκολα ηταν! μονο το πρωτο πρωτο ηταν μια λεπτομερεια π δεν θυμομασταν πολλοι απ οτι καταλαβα...επρεπε να κανεις παραγωγο κατα κατευθυνση επι το Δt..!
του καππου , ηταν λιγο κάππως όπως παντα..ίσως λιγο περισσότερο..ετσι μου φανηκαν εμενα δλδ..το πρωτο ηταν απλό , πορισμα απο stokes,τ επομενο ηταν να βγαλεις συναρτηση δυναμικου μεσω επικαμπυλιων ολοκληρωματων ..πως το ολοκληρωνες το θεμα επισης δεν ηξερα λολ..τζαμπα λιωσιμο :P και στ τελος είχε ένα κυβο που ηταν καλο θεμα..αλλα με λιγη φαντασια ελυνες τουλαχιστον το μισο (ελπιζω!)
αυταααα :D
προσωπικη αποψη κ καποιων φιλων δλδ! :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on September 16, 2008, 16:06:58 pm
Επίσης μία συμβουλή για όσους ενδεχομένως θα το ξαναδώσουν (κάτι που δεν το εύχομαι) είναι να διαβάσετε πρώτα τουλάχιστον μία φορά καλά την θεωρία και μετά να δείτε όλα τα παραδείγματα των βιβλίων.
Γιατί και να μην προλάβεις να δεις όλα τα παραδείγματα, εάν έχεις μία ολοκληρωμένη εικόνα του τι παίζει αυτόματα έχεις περισσότερες ευκαιρίες να γράψεις και μάλιστα καλά.
Όλη η θεωρία το Λογισμού ΙΙ είναι 200 το πολύ σελίδες χωρίς τα παραδείγματα..
εγω διαβασα πάνω από 700, ηξερα να λυνω και επικαμπύλια, και επιφανειακά, και διπλά - τριπλά, ήξερα να εφαρμοζω και τα θεωρήματα (gauss κτλ) αλλά παρόλα αυτά δεν το πέρασα.
Εχουν αλλάξει τα πράγματα Παναγιώτη....
(δες και τα θέματα στα downloads)
του Κάππου ήταν του στύλ "ξύστε τα νύχια σας και βγάλτε μια εξίσωση γι'αυτό"
και φυσικά τα θέματα για το 10 ήταν για 4'ωρες.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: smo on September 16, 2008, 16:52:30 pm
του Κάππου ήταν του στύλ "ξύστε τα νύχια σας και βγάλτε μια εξίσωση γι'αυτό"
>:( >:( >:( >:( >:( τωρα μας το λες καλα το ηξερες??????
και γιατι δεν ειπες τπτ και καθομασταν εκει μεσα και εξυνε ο καθενας οτι του κατεβαινε..... (το τι ειδα δεν περιγραφεται ;D)
η αλληλεγγυη πεθανε :'( :'( :'(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: (Stalin)^2 on September 16, 2008, 16:54:37 pm
του Κάππου ήταν του στύλ "ξύστε τα νύχια σας και βγάλτε μια εξίσωση γι'αυτό"
>:( >:( >:( >:( >:( τωρα μας το λες καλα το ηξερες??????
και γιατι δεν ειπες τπτ και καθομασταν εκει μεσα και εξυνε ο καθενας οτι του κατεβαινε..... (το τι ειδα δεν περιγραφεται ;D)
η αλληλεγγυη πεθανε :'( :'( :'(
;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kafeini on September 16, 2008, 20:20:17 pm
του Κάππου ήταν του στύλ "ξύστε τα νύχια σας και βγάλτε μια εξίσωση γι'αυτό"
>:( >:( >:( >:( >:( τωρα μας το λες καλα το ηξερες??????
και γιατι δεν ειπες τπτ και καθομασταν εκει μεσα και εξυνε ο καθενας οτι του κατεβαινε..... (το τι ειδα δεν περιγραφεται ;D)
η αλληλεγγυη πεθανε :'( :'( :'(
;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D
Καλά παιδιά είστε φοβεροί! κάθομαι κ γελάω μόνη κ με ακούει η αδερφή, κουνάει χαρακτηριστικά το κεφάλι πανω κάτω κ μ λέει: "κ σου 'λεγα εγώ το σαββατοκυριακο, μην διαβάζεις, βγες κ λίγο"
;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on September 17, 2008, 15:47:03 pm
;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D ;D
εγραψες
εγραψες
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: PallasFTW on June 19, 2009, 18:13:32 pm
Παιζει να εχει καποιος τις λυσεις του σεπτεμβριου 2007 να βγαλω καμια ακρη....θενκς
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ant on June 19, 2009, 18:23:45 pm
Τωρα ξεκινησα να λυνω και ειμαι ακομα στο 1...
Αν θες αργοτερα postαρε συγκεκριμενα ερωτηματα...
Αν θες αργοτερα postαρε συγκεκριμενα ερωτηματα...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ant on June 21, 2009, 16:17:13 pm
Και τωρα μπαινουμε στην παρανοια του μαθηματος... ( :D :D :D )
Θεμα 5 Σεπ '07: εχει ασχοληθει κανεις?
Για να βρω την καμπυλοτητα παιδευτηκα αρκετα, μηπως υπαρχει κανενα κολπακι που να μειωνει δραματικα τις πραξεις? ( ή απλως αντικαθιστας? )
^que^ ^que^ ^que^
Θεμα 5 Σεπ '07: εχει ασχοληθει κανεις?
Για να βρω την καμπυλοτητα παιδευτηκα αρκετα, μηπως υπαρχει κανενα κολπακι που να μειωνει δραματικα τις πραξεις? ( ή απλως αντικαθιστας? )
^que^ ^que^ ^que^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ant on June 21, 2009, 22:06:04 pm
Θεμα 6 2008 Καππος ( λυμενα )
1) Γιατι για το μοναδιαιο του ολοκληρωματος παιρνει το εξωτ διανυσμα των μερικων παραγωγων του r?
2) Οταν αντικαθιστα το dS με sqrt( 1 + x2 + y2 )dxdy γιατι χρειαζεται το ριζικο?
1) Γιατι για το μοναδιαιο του ολοκληρωματος παιρνει το εξωτ διανυσμα των μερικων παραγωγων του r?
2) Οταν αντικαθιστα το dS με sqrt( 1 + x2 + y2 )dxdy γιατι χρειαζεται το ριζικο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: chpapak on August 16, 2009, 12:39:35 pm
υπάρχει κάποιο καλό παιδί που έχει λύσει και μπορεί να ποστάρει την απάντηση από την 1η άσκηση των θεμάτων που έπεσαν τώρα τον Ιούνιο(είτε Α, είτε Β ομάδας)? εννοώ αυτό με τις μερικές παραγώγους~ (του κανάκη ήταν τώρα? θα σας γελάσω)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on August 21, 2009, 22:11:32 pm
Μπορεί κάποιος να μ πει τη λύση του τελευταίου ερωτήματος του πρώτου θέματος απο τον ιούλιο 2009 π είναι ανεβασμένα στο thmmy?Ξέρω τι κάνουμε για να το βρούμε απλα για μια λεπτομέρεια δν είμαι σίγουρος.Ευχαριστώ!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mostel on August 24, 2009, 18:01:06 pm
Μπορεί κάποιος να μ πει τη λύση του τελευταίου ερωτήματος του πρώτου θέματος απο τον ιούλιο 2009 π είναι ανεβασμένα στο thmmy?Ξέρω τι κάνουμε για να το βρούμε απλα για μια λεπτομέρεια δν είμαι σίγουρος.Ευχαριστώ!
Κατά μήκος της
Στέλιος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Errikos on September 13, 2009, 12:45:13 pm
Να βρεθεί η γωνία υπό την οποία τέμνονται οι ισοσταθμικές δύο συναρτήσεων της μορφής f(x^2 - y^2) , g(x,y).
Καμιά ιδέα?
Καμιά ιδέα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: goustafson on September 13, 2009, 14:13:39 pm
Μπορεί κάποιος να μ πει τη λύση του τελευταίου ερωτήματος του πρώτου θέματος απο τον ιούλιο 2009 π είναι ανεβασμένα στο thmmy?Ξέρω τι κάνουμε για να το βρούμε απλα για μια λεπτομέρεια δν είμαι σίγουρος.Ευχαριστώ!
Μήπως ξέρει κανεις τι κανουμε σε αυτο το 1ο θέμα του ιουλιου 2009;;;;;;;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Sage on March 17, 2010, 10:35:29 am
Οι σημειώσεις του Κάππου που υπάρχουν στο blackbrd αξίζουν?? να τις εκτυπώσω, ή τζαμπα κόπος? ::)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bakeneko on March 17, 2010, 13:24:24 pm
Δεν τις έχω δει, αλλά λογικά αξίζουν, αν ήταν διαφορετικά δε θα τις ανέβαζε :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pandora on March 17, 2010, 13:35:38 pm
αυτό που αξίζει από το blackboard είναι οι ασκήσεις του Κάππου
τα υπόλοιπα είναι θεωρία χωρίς καν λυμένα παραδείγματα
τα υπόλοιπα είναι θεωρία χωρίς καν λυμένα παραδείγματα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fishler on May 24, 2010, 16:41:24 pm
παιδια εχει κανεις θέματα σεπτεμ. 2009, σεπτ. κ ιουνη 2008;
ας κανει τον κοπο να τα ανεβασει η να επικοινωνησουμε να τα παρω.
ας κανει τον κοπο να τα ανεβασει η να επικοινωνησουμε να τα παρω.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilis1005 on May 26, 2010, 17:59:21 pm
παιδια εχει κανεις θέματα σεπτεμ. 2009, σεπτ. κ ιουνη 2008;
ας κανει τον κοπο να τα ανεβασει η να επικοινωνησουμε να τα παρω.
ας κανει τον κοπο να τα ανεβασει η να επικοινωνησουμε να τα παρω.
+1
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilis1005 on May 28, 2010, 20:54:18 pm
οταν μας λεει να δειξουμε οτι τα u,v μπορουν να γραφουν συναρτηση των x,y
τι αρκει να δειξουμε;
τι αρκει να δειξουμε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Orfikoss on May 28, 2010, 21:51:25 pm
Μήπως να βάλεις την άσκηση;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilis1005 on May 28, 2010, 22:23:37 pm
u3 + v2 + 2y2 - 4x=0
-u3 + 3v3 + x3 - 3y=0
Δειξτε οτι γυρω απο το σημειο (x,y,u,v)=(1,-1,1,-1) οι u,v μπορουν να ριστουν ως συναρτησεις των x,y : u=f(x,y) , v=g(x,y)
-u3 + 3v3 + x3 - 3y=0
Δειξτε οτι γυρω απο το σημειο (x,y,u,v)=(1,-1,1,-1) οι u,v μπορουν να ριστουν ως συναρτησεις των x,y : u=f(x,y) , v=g(x,y)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sidj0n on May 28, 2010, 22:25:03 pm
μου φαινεται οτι η ιακωβιανη τους δεν πρεπει να ειναι μηδεν..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mostel on May 28, 2010, 23:19:10 pm
u3 + v2 + 2y2 - 4x=0
-u3 + 3v3 + x3 - 3y=0
Δειξτε οτι γυρω απο το σημειο (x,y,u,v)=(1,-1,1,-1) οι u,v μπορουν να ριστουν ως συναρτησεις των x,y : u=f(x,y) , v=g(x,y)
-u3 + 3v3 + x3 - 3y=0
Δειξτε οτι γυρω απο το σημειο (x,y,u,v)=(1,-1,1,-1) οι u,v μπορουν να ριστουν ως συναρτησεις των x,y : u=f(x,y) , v=g(x,y)
Είναι κλασική άσκηση... Υπάρχουν πολλές λυμένες στο πορτοκαλί βιβλίο.... Μη περιμένεις να σου πω και σελίδα, γιατί δε το έχω μπροστά μου αυτή τη στιγμή. Η γενική ιδέα είναι η εξής:
Έστω F=0 η μία και G=0. Καταρχήν, τσεκάρεις αν F(1.-1,1,-1)=G(1,-1,1,-1).
Μετά παίρνεις ιακωβιανή των F,G ως προς u,v στο σημείο γύρω απ' το οποίο θες να ορίζονται (αν ορίζονται δηλαδή). Αν βγει διάφορη του 0, τότε ορίζεται μονοσήμαντα (γιατί?).
Στέλιος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mAn-_0lis on June 01, 2010, 22:36:09 pm
Ιούνιος 2009 - Θέματα Β΄
2(α΄) Να βρεθούν τα τοπικά ακρότατα της συνάρτησης
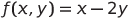
που βρίσκονται πάνω στη καμπύλη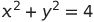
Απ' τη στιγμή που η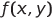 είναι πρώτης τάξης και δη ευθεία, που θα τα βρούμε τ' ακρότατα; Κρίσιμα σημεία δεν υπάρχουν.
είναι πρώτης τάξης και δη ευθεία, που θα τα βρούμε τ' ακρότατα; Κρίσιμα σημεία δεν υπάρχουν.
Θέλει απλά να του πούμε οτι δεν υφίστανται τοπικά ακρότατα; Ο_ο
2(α΄) Να βρεθούν τα τοπικά ακρότατα της συνάρτησης
που βρίσκονται πάνω στη καμπύλη
Απ' τη στιγμή που η
Θέλει απλά να του πούμε οτι δεν υφίστανται τοπικά ακρότατα; Ο_ο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilis1005 on June 01, 2010, 23:55:28 pm
Ιούνιος 2009 - Θέματα Β΄
2(α΄) Να βρεθούν τα τοπικά ακρότατα της συνάρτησης
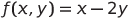
που βρίσκονται πάνω στη καμπύλη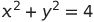
Απ' τη στιγμή που η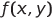 είναι πρώτης τάξης και δη ευθεία, που θα τα βρούμε τ' ακρότατα; Κρίσιμα σημεία δεν υπάρχουν.
είναι πρώτης τάξης και δη ευθεία, που θα τα βρούμε τ' ακρότατα; Κρίσιμα σημεία δεν υπάρχουν.
Θέλει απλά να του πούμε οτι δεν υφίστανται τοπικά ακρότατα; Ο_ο
2(α΄) Να βρεθούν τα τοπικά ακρότατα της συνάρτησης
που βρίσκονται πάνω στη καμπύλη
Απ' τη στιγμή που η
Θέλει απλά να του πούμε οτι δεν υφίστανται τοπικά ακρότατα; Ο_ο
πρεπει να βρεις τα ακροτατα της x-2y+λ(x2+y2-4)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mAn-_0lis on June 01, 2010, 23:58:28 pm
πρεπει να βρεις τα ακροτατα της x-2y+λ(x2+y2-4)
Οκ, όμως απο που προκύπτει αυτό; xD
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: papajim on June 02, 2010, 00:08:45 am
πρεπει να βρεις τα ακροτατα της x-2y+λ(x2+y2-4)
Οκ, όμως απο που προκύπτει αυτό; xD
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: The Stig on June 02, 2010, 00:35:35 am
πρεπει να βρεις τα ακροτατα της x-2y+λ(x2+y2-4)
Οκ, όμως απο που προκύπτει αυτό; xD
Απο την θεωρία των δεσμευμενων ακροτατων. Το λ είναι πολλαπλασιαστης Lagrange.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on June 04, 2010, 11:54:27 am
Μπορεί κάποιος να γράψει τα θέματα του Κάππου που μπήκαν τον Σεπτέμβριο 2009?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: τσαι-borg on June 04, 2010, 13:26:47 pm
http://blackboard.lib.auth.gr/webapps/portal/frameset.jsp?tab=courses&url=/bin/common/course.pl%3Fcourse_id%3D_250_1& (http://blackboard.lib.auth.gr/webapps/portal/frameset.jsp?tab=courses&url=/bin/common/course.pl%3Fcourse_id%3D_250_1&)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on June 04, 2010, 21:27:29 pm
Mπορείς να μ πεις π βρίσκονται?Μονο του Ιουνίου βρήκα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: png on June 04, 2010, 21:36:18 pm
Όλο το υλικό που έχει αναρτήσει ο Κάππος στο μπλακμπορντ ειναι σε αυτην την διευθυνση:
http://blackboard.lib.auth.gr/webapps/portal/frameset.jsp?tab=courses&url=/bin/common/course.pl%3Fcourse_id%3D_250_1&
έχει κάποια θέματα αναρτημένα (και λυμένα), όμως δεν ξέρω αν είναι αυτό που ζητάς.
Αν καταφέρεις να βρεις τελικά τα θέματα που ψάχνεις από κάποιον που έδωσε πέρυσι το μάθημα, μη διστάσεις να τα μοιραστείς με τους άτυχους της φετινής χρονιάς. Μαζί μας :P
http://blackboard.lib.auth.gr/webapps/portal/frameset.jsp?tab=courses&url=/bin/common/course.pl%3Fcourse_id%3D_250_1&
έχει κάποια θέματα αναρτημένα (και λυμένα), όμως δεν ξέρω αν είναι αυτό που ζητάς.
Αν καταφέρεις να βρεις τελικά τα θέματα που ψάχνεις από κάποιον που έδωσε πέρυσι το μάθημα, μη διστάσεις να τα μοιραστείς με τους άτυχους της φετινής χρονιάς. Μαζί μας :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on June 04, 2010, 22:29:04 pm
Δν τα χει αναρτήσει...απλα ρώτησα γιατί μπορεί να τα χει κάποιος π το δωσε τότε και θα μπορούσε να τα γράψει εδώ..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nemdam on June 05, 2010, 16:36:30 pm
Αν μπορεί κάποιος να ανεβάσει λύσεις των θεμάτων παλαιότερων ετών, και κυρίως ιουνίου 2009 θα κάνει μεγάλη χάρη σε πολλούς...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 05, 2010, 18:38:20 pm
αργοτερα του περσινου ιουνη 8))
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 05, 2010, 18:41:50 pm
του ΣΕΠ2008 οπως τα εχει ανεβασει ο καππος δε λειπει κατι απο την εκφωνηση της 6?
υπαρχουν αυτες οι εκφωνησεις?
υπαρχουν αυτες οι εκφωνησεις?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: png on June 05, 2010, 20:25:58 pm
Η συζητηση για τα εικονικά γουιντοοζ εδώ (https://www.thmmy.gr/smf/index.php?topic=40228).
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 05, 2010, 22:51:42 pm
επισυναπτω λυμενο το θεμα 1 που ελεγα παραπανω
δεν εχω ουτε καλωδιο για το κινητο, γιατι μου το χουνε παρει και δε μου το γυρισανε ποτε :D
και ετσι ανοιξα το ασυρματο, τραβηξα με το κινητο, και τις ανεβασα απο το opera του κινητου
χαχαχαχαχαχαχ ;D
δεν εχω ουτε καλωδιο για το κινητο, γιατι μου το χουνε παρει και δε μου το γυρισανε ποτε :D
και ετσι ανοιξα το ασυρματο, τραβηξα με το κινητο, και τις ανεβασα απο το opera του κινητου
χαχαχαχαχαχαχ ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 05, 2010, 23:01:05 pm
2ο κ 3ο θεμα
edit : απο σας ψηνεται κανεις να ανεβασει τιποτα λυμενο? :P :P :P
2o edit : χαχα τι μαλακας ειμαι :D
ξεχασα να λυσω το β και γ ερωτημα του 3ου θεματος :D :D
σε λιγο :P
edit : απο σας ψηνεται κανεις να ανεβασει τιποτα λυμενο? :P :P :P
2o edit : χαχα τι μαλακας ειμαι :D
ξεχασα να λυσω το β και γ ερωτημα του 3ου θεματος :D :D
σε λιγο :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: il capitano on June 05, 2010, 23:10:16 pm
Ψηνομαι εγω...
αν και ειναι πανω και στο bb για οποιον δεν τα ειδε, λυσεις του ιουνη 2009
edit: στην Δ.Α.
αν και ειναι πανω και στο bb για οποιον δεν τα ειδε, λυσεις του ιουνη 2009
edit: στην Δ.Α.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 00:51:02 am
καποια βοηθεια για σεπτεμβριο 2008 θεμα 1ο, ερωτημα β ????
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: michalisvrachimis on June 06, 2010, 01:37:23 am
πες τι λεει......
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 01:48:42 am
(http://img46.imageshack.us/img46/9259/asdwp.jpg)
αν δε φαινεται καλα, ειναι w=y * x2 * ez
το β' ερωτημα παρακαλω :P :P
αν δε φαινεται καλα, ειναι w=y * x2 * ez
το β' ερωτημα παρακαλω :P :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: michalisvrachimis on June 06, 2010, 02:01:39 am
(http://img46.imageshack.us/img46/9259/asdwp.jpg)
αν δε φαινεται καλα, ειναι w=y * x2 * ez
το β' ερωτημα παρακαλω :P :P
dw/dt=θw/θχ.dx/dt+θw/θψ.dψ/dt+θw/θΖ.dΖ/dtαν δε φαινεται καλα, ειναι w=y * x2 * ez
το β' ερωτημα παρακαλω :P :P
το dx/dt=-F1t/F1x
TO dψ/dt=-F2t/F2ψ και
TO dΖ/dt=-F3t/F3Ζ
οπου F1= x^3.t^2+x.t^3+x^2+1 kai F2=.... F3=.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 02:06:44 am
και εγω ετσι το σκεφτηκα :D :D :D :D
αλλα επειδη δεν εχει γραψει και ο τυπας ολοκληρη την εκφωνηση,
ειχα καποιες σκεψεις να αποδειξω ξερω γω οτι τα x,y,z ειναι συναρτησεις του t
αλλα μαλλον δε το θελει
οκ ευχαριστω :) :)
at your services και γω :P
αλλα επειδη δεν εχει γραψει και ο τυπας ολοκληρη την εκφωνηση,
ειχα καποιες σκεψεις να αποδειξω ξερω γω οτι τα x,y,z ειναι συναρτησεις του t
αλλα μαλλον δε το θελει
οκ ευχαριστω :) :)
at your services και γω :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mAn-_0lis on June 06, 2010, 02:11:06 am
[εγκυκλοπαιδικά:] O χαρακτήρας 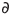 δεν είναι θ και διαβάζεται "del".
δεν είναι θ και διαβάζεται "del".
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 02:12:29 am
νταξ
αλλα ο καππος ειπε οτι δε κοβει τπτ απο κει, και θ να το γραφεις :P :P
αλλα ο καππος ειπε οτι δε κοβει τπτ απο κει, και θ να το γραφεις :P :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nikitas350 on June 06, 2010, 02:17:25 am
Δεν διαβάζεται ούτε θ ούτε del http://en.wikipedia.org/wiki/Del
Στα αγγλικά η μερική παράγωγος της f ως προς x λέγεται partial f partial x η derivative of f with respect to x.
Πιστεύω δλδ ότι η καλύτερη ονομασία ειναι "partial"
Στα αγγλικά η μερική παράγωγος της f ως προς x λέγεται partial f partial x η derivative of f with respect to x.
Πιστεύω δλδ ότι η καλύτερη ονομασία ειναι "partial"
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: il capitano on June 06, 2010, 02:29:12 am
Ενα συμβολο ειναι μπορεις να το ονομασεις οπως θες (το λες "θητα" γιατι μοιαζει με το γραμμα θητα). Το σωστο θα ηταν να λες μερικη παραγωγος της f ως προς x, αλλα για δυντομια "θητα f θητα x".
Το ιδιο και και με την κανονικη παραγωγο. Κανονικα ειναι παραγωγος της f ως προς x, αλλα μπορεις και να πεις "ντε f ντε x", χωρις παρανοηση...θεμα συμβασης ειναι!
Το ιδιο και και με την κανονικη παραγωγο. Κανονικα ειναι παραγωγος της f ως προς x, αλλα μπορεις και να πεις "ντε f ντε x", χωρις παρανοηση...θεμα συμβασης ειναι!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nikitas350 on June 06, 2010, 02:55:58 am
Ενα συμβολο ειναι μπορεις να το ονομασεις οπως θες (το λες "θητα" γιατι μοιαζει με το γραμμα θητα). Το σωστο θα ηταν να λες μερικη παραγωγος της f ως προς x, αλλα για δυντομια "θητα f θητα x".
Το ιδιο και και με την κανονικη παραγωγο. Κανονικα ειναι παραγωγος της f ως προς x, αλλα μπορεις και να πεις "ντε f ντε x", χωρις παρανοηση...θεμα συμβασης ειναι!
Το ιδιο και και με την κανονικη παραγωγο. Κανονικα ειναι παραγωγος της f ως προς x, αλλα μπορεις και να πεις "ντε f ντε x", χωρις παρανοηση...θεμα συμβασης ειναι!
Φυσικα, το θέμα είναι βέβαια να μπορείς να συνεννοείσαι με τους άλλους, αν δηλαδή δεν λέει κανένας το σύμβολο όπως το λές εσύ τότε έχεις πρόβλημα...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 10:12:43 am
δε μπορω να λυσω και το 2ο θεμα σωστα :P :P
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
η περιοχη που περιοριζομαστε για τα σημεια (x,y) ειναι το τριγωνο ΑΟΒ οπου Α(-4,0) Ο(0,0) Β (0,-4)
αν το ψαξουμε γενικα σε ολο το R, στασιμο σημειο η f εχει στο (0,0) αλλα δεν παιρνει μεγιστη τιμη, ελαχιστη παιρνει εκει :D
αλλα αυτο δε νομιζω να μας ενδιαφερει, καθολου μαλλον ::)
εντωμεταξυ, ξερω οτι η μεγιστη τιμη θα ειναι το f ( -2 , -2 ) αλλα δε μπορω να εξηγησω γιατι :D :D :D :D :D :D :D
help :'( :'( :'(
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
η περιοχη που περιοριζομαστε για τα σημεια (x,y) ειναι το τριγωνο ΑΟΒ οπου Α(-4,0) Ο(0,0) Β (0,-4)
αν το ψαξουμε γενικα σε ολο το R, στασιμο σημειο η f εχει στο (0,0) αλλα δεν παιρνει μεγιστη τιμη, ελαχιστη παιρνει εκει :D
αλλα αυτο δε νομιζω να μας ενδιαφερει, καθολου μαλλον ::)
εντωμεταξυ, ξερω οτι η μεγιστη τιμη θα ειναι το f ( -2 , -2 ) αλλα δε μπορω να εξηγησω γιατι :D :D :D :D :D :D :D
help :'( :'( :'(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on June 06, 2010, 11:09:11 am
δε μπορω να λυσω και το 2ο θεμα σωστα :P :P
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
Kάποιος?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Groucho on June 06, 2010, 11:17:06 am
δε μπορω να λυσω και το 2ο θεμα σωστα :P :P
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
Kάποιος?
Θελει ολικα ακροτατα.Βρες στασιμα σημεια στο εσωτερικο του τριγωνου.Βρες τυχον στασιμα σημεια στο συνορο(χ=0,ψ=0,χ+ψ=4) και βρες και τις τιμες της f στις κορυφες του τριγωνου καθως και τις τιμες της σ ολα τα στασιμα που βρηκες.Η μεγαλυτερη ειναι το μεγιστο.Η μικροτερη το ελαχιστο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 11:19:15 am
3o θεμα {πριν ειχα κανει λαθος και ειχα γραψει 2ο, σορρυ αν σας μπερδεψα :D }
στο εμβαδο με καρτεσιανες, στο 1ο ολοκληρωμα εβαλα το προσημο πλην, γιατι τα ορια τα εβαλα αναποδα
και ειπα να μη κανω κι αλλη μουτζουρα! :D ;D
ευχαριστω ale26, θα το ψαξω ετσι και θα το ανεβασω αμα το λυσω :P
στο εμβαδο με καρτεσιανες, στο 1ο ολοκληρωμα εβαλα το προσημο πλην, γιατι τα ορια τα εβαλα αναποδα
και ειπα να μη κανω κι αλλη μουτζουρα! :D ;D
ευχαριστω ale26, θα το ψαξω ετσι και θα το ανεβασω αμα το λυσω :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 11:51:18 am
Τωρα αυτο να μου πει καποιος τον τυπο ^beg^
(http://img46.imageshack.us/img46/6881/16788212.jpg)
(http://img46.imageshack.us/img46/6881/16788212.jpg)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 12:00:40 pm
μπορει καποιος να μου πει λιγο πως παει το πραγμα με τις μερικες παραγωγους σε πλεγμενες συναρτησεις? :)
ας πουμε αν εχουμε F(x,y,z,w)=0 και G(x,y,z,w)=0 πως βρισκω θz/θx?(ειναι ουσιαστικα και το θεμα που εχει λυθει πιο πανω...απλα γενικα τα εχω μπερδεψει λιγο :-\) ).
ας πουμε αν εχουμε F(x,y,z,w)=0 και G(x,y,z,w)=0 πως βρισκω θz/θx?(ειναι ουσιαστικα και το θεμα που εχει λυθει πιο πανω...απλα γενικα τα εχω μπερδεψει λιγο :-\) ).
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 12:05:42 pm
πορτοκαλι σελιδα 242 :P :P :P :P :P :P :P :P :P :P
δε σε καλυπτει? :???:
δε σε καλυπτει? :???:
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 12:12:22 pm
ρε συ το διαβασα απλα δεν μπορω να τα ξεκαθαρισω στο μυαλο μ..αν μπορουσες να μ τ εξηγησεις λιγο θα το εκτιμουσα γιατι πραγματικα εχω κολλησει..(ξερω οτι ειναι χαζο :P)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 12:18:23 pm
πωωωωω :P :D
κρατα στο μυαλο σου τον τυπο 1.17 σελιδα 243
μονο αυτον! ;D
να θυμασαι οτι πριν βρεις αυτο,
θα πρεπει να υπολογιζεις την ιακωβιανη του παρονομαστη και να ειναι διαφορη του μηδενος
και προσπαθησε να ξεκαθαρισεις τι ειναι η Ιακωβιανη :P :P :P
κρατα στο μυαλο σου τον τυπο 1.17 σελιδα 243
μονο αυτον! ;D
να θυμασαι οτι πριν βρεις αυτο,
θα πρεπει να υπολογιζεις την ιακωβιανη του παρονομαστη και να ειναι διαφορη του μηδενος
και προσπαθησε να ξεκαθαρισεις τι ειναι η Ιακωβιανη :P :P :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 12:26:05 pm
α οκ...τελικα ηταν πολυ πιο απλο απ ο,τι νομιζα :P
σ ευχαριστω τερμαααααααααααα :D :D :D ;) :D :D :D
σ ευχαριστω τερμαααααααααααα :D :D :D ;) :D :D :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 06, 2010, 13:17:46 pm
δε μπορω να λυσω και το 2ο θεμα σωστα :P :P
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
η περιοχη που περιοριζομαστε για τα σημεια (x,y) ειναι το τριγωνο ΑΟΒ οπου Α(-4,0) Ο(0,0) Β (0,-4)
αν το ψαξουμε γενικα σε ολο το R, στασιμο σημειο η f εχει στο (0,0) αλλα δεν παιρνει μεγιστη τιμη, ελαχιστη παιρνει εκει :D
αλλα αυτο δε νομιζω να μας ενδιαφερει, καθολου μαλλον ::)
εντωμεταξυ, ξερω οτι η μεγιστη τιμη θα ειναι το f ( -2 , -2 ) αλλα δε μπορω να εξηγησω γιατι :D :D :D :D :D :D :D
help :'( :'( :'(
ειναι αυτο:
(http://img7.imageshack.us/img7/55/51691369.jpg)
η περιοχη που περιοριζομαστε για τα σημεια (x,y) ειναι το τριγωνο ΑΟΒ οπου Α(-4,0) Ο(0,0) Β (0,-4)
αν το ψαξουμε γενικα σε ολο το R, στασιμο σημειο η f εχει στο (0,0) αλλα δεν παιρνει μεγιστη τιμη, ελαχιστη παιρνει εκει :D
αλλα αυτο δε νομιζω να μας ενδιαφερει, καθολου μαλλον ::)
εντωμεταξυ, ξερω οτι η μεγιστη τιμη θα ειναι το f ( -2 , -2 ) αλλα δε μπορω να εξηγησω γιατι :D :D :D :D :D :D :D
help :'( :'( :'(
στο συγκεκριμενο τοπο ειναι οντως ελαχιστο..
μετα θα πας πανω στην καμπυλη που σου δινει η οποια ειναι η y=-x-4
τα ακροτατα εκει πανω μπορεις να τα βρεις με δυο τροπους:
1)αντικαθιστας στην f=xy το y=-x-4 και βρισκεις ακροτατα για την f(x)
2)ψαχνεις δεσμευμενα ακροτατα για την f=xy+λ(y+x+4)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 13:24:21 pm
και στο εσωτερικο του τριγωνου τι γινεται? :P :P :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: il capitano on June 06, 2010, 13:28:57 pm
Τωρα αυτο να μου πει καποιος τον τυπο ^beg^
(http://img46.imageshack.us/img46/6881/16788212.jpg)
Λοιπων εδω ο τόπος ολοκλήρωσης είναι η τομή του κυλίνδρου x2+y2=4, και του κωνου z2=x2+y2 (το εξωτερικο μερος), με τα επίπεδα z=0,z=2. (http://img46.imageshack.us/img46/6881/16788212.jpg)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 13:31:35 pm
εισαι θεος ^kissy^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 06, 2010, 13:36:37 pm
νομιζω οτι:
αφου η f δεν παρουσιαζει ακροτατα στο χωρο γενικα,τοτε αν την περιορισεις σε καποιο τοπο τα ακροτατα της θα ειναι στο συνορο του τοπου αυτου.
αν παρουσιαζει γενικα ακροτατα τα οποια συμβαινει να ειναι μεσα στον τοπο αυτο, τοτε πρεπει να τα συγκρινεις με τα ακροτατα στο συνορο για να βγαλεις το τελικο συμπερασμα.
αφου η f δεν παρουσιαζει ακροτατα στο χωρο γενικα,τοτε αν την περιορισεις σε καποιο τοπο τα ακροτατα της θα ειναι στο συνορο του τοπου αυτου.
αν παρουσιαζει γενικα ακροτατα τα οποια συμβαινει να ειναι μεσα στον τοπο αυτο, τοτε πρεπει να τα συγκρινεις με τα ακροτατα στο συνορο για να βγαλεις το τελικο συμπερασμα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 13:39:08 pm
αφου η f δεν παρουσιαζει ακροτατα στο χωρο γενικα,τοτε αν την περιορισεις σε καποιο τοπο τα ακροτατα της θα ειναι στο συνορο του τοπου αυτου.
εγω νομιζω οτι αυτο δεν ισχυει και αυτο ειναι το προβλημα μου :-[Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niels on June 06, 2010, 14:40:38 pm
Ισχύει. Ας πάρουμε μία f(x) και θέλουμε να βρούμε το μέγιστο στο [α,β]. Αν δεν παρουσιάζει μέγιστο στο (α,β) τότε η μεγιστη τιμή θα είναι η μεγαλύτερη από τις f(α) και f(β). Έτσι είναι κι αυτό
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niels on June 06, 2010, 14:44:01 pm
Γενικά θα παίρνεις όλα τα μεγιστα που παρουσιάζει στο R2, θα κρατάς όσα είναι μέσα στον τόπο που θες. Μετά θα βρίσκεις και τα μέγιστα πάνω στον τόπο, θα τα συγκρίνεις όλα αυτά και θα βρίσκεις το μεγαλύτερο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 15:29:40 pm
αφου η f δεν παρουσιαζει ακροτατα στο χωρο γενικα,τοτε αν την περιορισεις σε καποιο τοπο τα ακροτατα της θα ειναι στο συνορο του τοπου αυτου.
εγω νομιζω οτι αυτο δεν ισχυει και αυτο ειναι το προβλημα μου :-[Όπως τα είπε και ο Νiels ... Έχει άσκηση όμοια σελ 346 πορτοκαλί
EDIT: Χρειάζομαι help εδώ... Αφού τα y είναι σταθερά και το μοναδιαίο της ευθείας είναι 1,0,1
ΠΩΣ ΛΥΝΕΤΑΙ ΤΟ γ !!!! ?
(http://img38.imageshack.us/img38/2702/96571133.png)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 15:43:44 pm
η τομη των 2 επιπεδων ειναι η ευθεια 2x + y - 2z = 0
για να ειναι y=0 στο διανυσμα που ειναι παραλληλο στην ευθεια
θα πρεπει η ευθεια να ειναι παραλληλη στο επιπεδο zOx,αλλα αυτο δεν ισχυει ισχυει :D :P
αρα καπου εκανες λαθος στους υπολογισμους.
θα ανεβαζα τη δικη μου λυση, αλλα εκανα μαλακια
γιατι ο il capitano μου ειπε πως στην ευθεια αx+βy+γz=0
ειναι παραλληλο το διανυσμα (α,β,γ) αλλα αυτο δεν ισχυει, το διανυσμα αυτο ειναι καθετο στην ευθεια
αρα, μπορεις να μου πεις πως βρισκουμε ενα διανυσμα καθετο σε μια γνωστη ευθεια?? :D :D :D :D :D :D
το ξερω οτι ειναι πολυ γελοιο αυτο που ρωταω αλλα....... ;D
για να ειναι y=0 στο διανυσμα που ειναι παραλληλο στην ευθεια
θα πρεπει η ευθεια να ειναι παραλληλη στο επιπεδο zOx,
θα ανεβαζα τη δικη μου λυση, αλλα εκανα μαλακια
γιατι ο il capitano μου ειπε πως στην ευθεια αx+βy+γz=0
ειναι παραλληλο το διανυσμα (α,β,γ) αλλα αυτο δεν ισχυει, το διανυσμα αυτο ειναι καθετο στην ευθεια
αρα, μπορεις να μου πεις πως βρισκουμε ενα διανυσμα καθετο σε μια γνωστη ευθεια?? :D :D :D :D :D :D
το ξερω οτι ειναι πολυ γελοιο αυτο που ρωταω αλλα....... ;D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 15:46:15 pm
δεν ξέρω μάλλον είναι χαζό το θέμα αλλά έχω κολλήσει...
Για αυτό που ρώτησες αν εννοείς διανυσμα παράλληλο με ευθεία , αυτό που κάνω εγώ αν και λίγο μπακάλικο είναι να πάιρνω 2 σημεία της ευθείας και να τα ενώνω :p μετά αμα θες πάρε το μοναδιαίο του...
edit: π.χ. για χ=0 Α, χ=-1 Β-> ΑΒ//ε
Για αυτό που ρώτησες αν εννοείς διανυσμα παράλληλο με ευθεία , αυτό που κάνω εγώ αν και λίγο μπακάλικο είναι να πάιρνω 2 σημεία της ευθείας και να τα ενώνω :p μετά αμα θες πάρε το μοναδιαίο του...
edit: π.χ. για χ=0 Α, χ=-1 Β-> ΑΒ//ε
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 15:48:18 pm
επισυναπτω τη λυση με το λαθος διανυσμα u, u1
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 15:55:01 pm
επισυναπτω τη λυση με το λαθος διανυσμα u, u1
Γρίφε κάνε μου τη χάρη δοκίμασε κάτι... Πρόσθεσε τις 2 ευθείες...
(Εξισώσεις κατα μέλη...)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 16:02:01 pm
α ναι οντως, βγαινει y=2 ::) ::) ::)
τωρα τι κανουμε? :D
τωρα τι κανουμε? :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 16:05:33 pm
α ναι οντως, βγαινει y=2 ::) ::) ::)
τωρα τι κανουμε? :D
Off-Topic... /Αύριο θα γράψω Κάππο και θα κοπώ απο ρόθο... ;D :D /τωρα τι κανουμε? :D
Απλά ξερώ γώ... να υποθέσουμε οτι όποιος τα μετέφερε τα αντέγραψε λάθος? BTW οι ευθείες αναγκαστικά έχουν 2 μεταβλητές , αλλιώς είναι επίπεδο πχ το 2χ+υ-2ζ=0 , Right?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: billakos on June 06, 2010, 16:06:12 pm
αληθεια θεματα ποιοι βαζουν?μπορουμε να διαλεξουμε?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Groucho on June 06, 2010, 16:07:51 pm
ποσο βρισκετε τη μεγιστη τιμη της f στο 2ο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on June 06, 2010, 16:08:42 pm
αληθεια θεματα ποιοι βαζουν?μπορουμε να διαλεξουμε?
Noμίζω βάζουν όλοι. Ανεξάρτητα από το επιθετο σου δλδ (α-κ ή λ-ω) θα γράψεις ολα τα θέματα.Αυτό που θυμάμαι είναι πάντως ότι στο λογισμό πάντα υπάρχουν δύο ομάδες θεμάτων.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 16:09:12 pm
ποσο βρισκετε τη μεγιστη τιμη της f στο 2ο?
EDIT: Σορρυ ναι... Δές σελ 346 πορτοκαλί οπως είπα και πρινTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 16:10:23 pm
αυτο με το τριγωνο που λεγαμε πριν :P
ΥΓ:
αφιερωμενο σε μας που δινουμε :D
https://www.youtube.com/watch?v=3pExRpbsAK8
ΥΓ:
αφιερωμενο σε μας που δινουμε :D
https://www.youtube.com/watch?v=3pExRpbsAK8
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Groucho on June 06, 2010, 16:21:27 pm
θανκ γιου
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: oustas on June 06, 2010, 17:28:21 pm
Για το γ ερώτημα υπάρχει στην σελίδα 219 (άσκηση 25).
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 17:31:57 pm
νταξει
αρα βρηκαμε λαθος διανυσματα και γω και ο ScytheB :D
αρα βρηκαμε λαθος διανυσματα και γω και ο ScytheB :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 17:56:36 pm
Για το γ ερώτημα υπάρχει στην σελίδα 219 (άσκηση 25).
νταξει
αρα βρηκαμε λαθος διανυσματα και γω και ο ScytheB :D
αρα βρηκαμε λαθος διανυσματα και γω και ο ScytheB :D
Ναι αλλά η μέθοδος με τις οριζουσες πως προκύπτει?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 18:03:22 pm
αναλυτικη γεωμετρια, αμα πας στα pdf (για πολ. μηχ.) του κεχαγια με λυμενες ασκησεις θα βρεις τα παντα ολα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 18:17:09 pm
Ναι , άσχετο το βρήκα καταλάθως , ο τύπος προφανώς παίρνει εξωτερικό γινόμενο των καθέτων διανυσμάτων των 2 επιπέδων αφού εκεί που θα είναι και τα 2 κάθετα θα είναι στην τομή τους...
Μέχρι εδώ βέβαια Ok...
Ο εγκεφαλος μου μου πέταξε BSOD οταν συνέχισα με τα θέματα στο ηλεκτρονικό...
Μέχρι εδώ βέβαια Ok...
Ο εγκεφαλος μου μου πέταξε BSOD οταν συνέχισα με τα θέματα στο ηλεκτρονικό...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on June 06, 2010, 18:19:34 pm
Ναι , άσχετο το βρήκα καταλάθως , ο τύπος προφανώς παίρνει εξωτερικό γινόμενο των καθέτων διανυσμάτων των 2 επιπέδων αφού εκεί που θα είναι και τα 2 κάθετα θα είναι στην τομή τους...
Μέχρι εδώ βέβαια Ok...
Ο εγκεφαλος μου μου πέταξε BSOD οταν συνέχισα με τα θέματα στο ηλεκτρονικό...
Μέχρι εδώ βέβαια Ok...
Ο εγκεφαλος μου μου πέταξε BSOD οταν συνέχισα με τα θέματα στο ηλεκτρονικό...
Κάτι τέτοιο δηλαδή?
(http://x86code.com/hole/hole/bsod.bmp)
;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 18:43:58 pm
να ρωτησω κατι για ακροτατα?
αν εχω συναρτηση 3 μεταβλητων σαγμα που εχω? :-\
αν εχω συναρτηση 3 μεταβλητων σαγμα που εχω? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 18:48:09 pm
στο σημειο Ρ αν
fx(Ρ) = fy(P) = fz(P) = 0
διορθωση:και η D2 στο Ρ πρεπει να ειναι αρνητικη
fx(Ρ) = fy(P) = fz(P) = 0
διορθωση:και η D2 στο Ρ πρεπει να ειναι αρνητικη
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: png on June 06, 2010, 18:49:55 pm
άπλυτε γερά! θα σκίσεις αυτή τη φορά!
\\δεν έχω ιδέα από λογισμό ΙΙ, αλλά με πείθει η βεβαιότητά σου :D :P
\\δεν έχω ιδέα από λογισμό ΙΙ, αλλά με πείθει η βεβαιότητά σου :D :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 18:53:23 pm
άπλυτε γερά! θα σκίσεις αυτή τη φορά!
\\δεν έχω ιδέα από λογισμό ΙΙ, αλλά με πείθει η βεβαιότητά σου :D :P
συμφωνω.. ;)\\δεν έχω ιδέα από λογισμό ΙΙ, αλλά με πείθει η βεβαιότητά σου :D :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 18:55:39 pm
στο σημειο Ρ αν
fx(Ρ) = fy(P) = fz(P) = 0
και η D3 στο Ρ πρεπει να ειναι αρνητικη
fx(Ρ) = fy(P) = fz(P) = 0
και η D3 στο Ρ πρεπει να ειναι αρνητικη
Άπλυτε βσκ ξανακοίτα σελ 306... μήπως μπερδεύτηκες...
Ή καλύτερα μη κοιτάς στο forum κάτσε λύσε τπτ... :D :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: lindou on June 06, 2010, 18:58:39 pm
βασικα στην σ.306 δε λεει απλα για θετικα και αρνητικα ορισμενη οριζουσα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 18:59:18 pm
εεε, πες εσυ που θα εχει σαγματικο ScytheB! :???: :???: :???:
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 19:01:21 pm
Δεν ξέρω για R3 σίγουρα αλλά υποθέτω οτι όμοια η D2 να είναι αρνητική αν δείς στο R2
Όμως εσύ περιέγραψες το σχετικό μέγιστο (σχεδον ακριβώς) ... :P
Εdit:Ξέρει κανείς να πεί σίγουρα???
Όμως εσύ περιέγραψες το σχετικό μέγιστο (σχεδον ακριβώς) ... :P
Εdit:Ξέρει κανείς να πεί σίγουρα???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 19:11:11 pm
(http://wbhsweb.com/hiller/john-bonham/psyduck.gif)
ααααα μαλακια ειπα χαχαχα :D :D :D
ναι οντως
οποιος ξερει ας μας βοηθησει! ^seestars^
ααααα μαλακια ειπα χαχαχα :D :D :D
ναι οντως
οποιος ξερει ας μας βοηθησει! ^seestars^
αν εχω συναρτηση 3 μεταβλητων σαγμα που εχω? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on June 06, 2010, 19:11:51 pm
Ρε παιδια θυμάται κανείς τα θέματα σεπτεμβρίου 2009 του κάππου?Τα ολοκληρώματα π ειχε στο 1ο κ 2ο θέμα?Οχι αυτούσια, τι ειδους ήταν,γτ τα χα κάνει λάθος κ θέλω να τα προσέξω αυτή τη φορα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 06, 2010, 19:19:34 pm
αν το D2<0 τοτε δεν εχω max ουτε min αρα σαγματικο..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 19:20:44 pm
τελεια
και απο που το συμπεραινουμε αυτο?!
edit : βασικα, τι ρωταω? αφου για να εχει μεγιστο/ελαχιστο πρεπει D2>0 , αρα αμα δεν ισχυει αυτο τοτε ειναι σαγματικο
και απο που το συμπεραινουμε αυτο?!
edit : βασικα, τι ρωταω? αφου για να εχει μεγιστο/ελαχιστο πρεπει D2>0 , αρα αμα δεν ισχυει αυτο τοτε ειναι σαγματικο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 19:22:35 pm
τελεια
και απο που το συμπεραινουμε αυτο?!
An D2 αρνητικό τότε είναι ετερόσημες οι 2 παράγωγοι και απο τη μια κατεβαίνει απο την άλλει ανεβαίνει στη μέση στραβώνει κλπ κλπ κλπ... Άρα σχηματίζει σάγμακαι απο που το συμπεραινουμε αυτο?!
Λεπτομέρειες σελ 297+κανα 3
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niels on June 06, 2010, 19:31:12 pm
α ναι οντως, βγαινει y=2 ::) ::) ::)
τωρα τι κανουμε? :D
τωρα τι κανουμε? :D
Τώρα βάζετε όπου y 2 και προκύπτουν 2 εξισώσεις που παριστάνουν την ίδια ευθεία(η οποία είναι και η ευθεία που ζητάτε)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 19:36:53 pm
ρε niels αφού το διάνυσμα των 2 επιπέδων στο βιβλίο βγαίνει άλλο... με x σταθ., όμοια άσκηση
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 06, 2010, 19:37:03 pm
πολικες συντεταγμενες στο χωρο δεν υφιστανται ετσι?
θεμα 4 σε αυτα που συζηταμε μαλλον εννοει κυλινδρικες??
θεμα 4 σε αυτα που συζηταμε μαλλον εννοει κυλινδρικες??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 19:39:50 pm
ναι μωρέ... πολικές = κυλινδρικές για ζ=0 και αντίστροφα
Τελικά τι παίζει με το θέμα 1 γ ερώτημα... Θα μου εξηγήσει κάποιος γιατί η μία μέθοδος βγάζει άλλα?
Τελικά τι παίζει με το θέμα 1 γ ερώτημα... Θα μου εξηγήσει κάποιος γιατί η μία μέθοδος βγάζει άλλα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 19:45:04 pm
cookie fοr noul
ΥΓ : δε φαινονται και πολυ καλα
δε φταιω εγω :(
τα ουμπουντα φταινε που ειναι ανιωθα και δεν πιανουνε το σκαννερ μου :P
ΥΓ : δε φαινονται και πολυ καλα
δε φταιω εγω :(
τα ουμπουντα φταινε που ειναι ανιωθα και δεν πιανουνε το σκαννερ μου :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 19:46:55 pm
Ωραίος γρίφε.. Όλα μαζεμένα :P :P
Με το δικό μας βρήκες τελικά τι κάναμε λάθος?
εδιτ 1-γ γιατί αμα πάρω ζ=χ+1 ευθεία βγάζω άλλο παράλληλο ,(δηλαδή με y=2)
Με το δικό μας βρήκες τελικά τι κάναμε λάθος?
εδιτ 1-γ γιατί αμα πάρω ζ=χ+1 ευθεία βγάζω άλλο παράλληλο ,(δηλαδή με y=2)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 19:47:43 pm
ποιο λες?
τις 2 ευθειες?
τις 2 ευθειες?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 20:01:43 pm
Άκυρο... Τελικά είχα δίκιο απο την αρχή , το βιβλίο έχει ενα χ αντι για y... Τελικά γίνομαι πολυ χαζός παραμονές εξετάσεων....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fosa on June 06, 2010, 20:03:02 pm
Ρε παιδιά μ λετε όλοι για το blackboard,εκεί έχει τις λύσεις του ΙΟΥΝΙΟΥ, εγω ρωτάω αν έχετε του ΣΕΠΤΕΜΒΡΙΟΥ.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ScytheB on June 06, 2010, 20:03:50 pm
Ρε παιδιά μ λετε όλοι για το blackboard,εκεί έχει τις λύσεις του ΙΟΥΝΙΟΥ, εγω ρωτάω αν έχετε του ΣΕΠΤΕΜΒΡΙΟΥ.
Ωχ... ::) ::) ::) σορρυ Fosa βιάστηκα... Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 06, 2010, 20:24:58 pm
για noul
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: noul on June 06, 2010, 21:04:33 pm
ευχαριστω!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on June 07, 2011, 17:07:21 pm
Αναπολώντας το 4αρι που πήρα το Σεπτέμβρη στο Λογισμό ΙΙ επειδή δεν έπιασα 1,5 μονάδα στα θέματα β ενότητας, και κοιτάζοντας τώρα τις αντίστοιχες λύσεις, μου γεννάται η ανυπέρβλητη επιθυμία να χαστουκίσω τον Κάππο. Ειν' κακό?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Nerevar on June 07, 2011, 19:18:38 pm
Μετα απο την τεταρτη φορα που κοβεσαι στον λογισμο 2,ειναι απολυτως φυσιολογικο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on June 08, 2011, 00:03:18 am
Μετρητής κομμένων γραπτών στον Λογισμό ΙΙ :
(http://www.gifs.net/Animation11/Webdesign_Elements/Counters/gorrila_counter.gif)
(http://www.gifs.net/Animation11/Webdesign_Elements/Counters/gorrila_counter.gif)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zeus90 on June 09, 2011, 00:03:29 am
Έχει κανείς τις λύσεις από την πρώτη ενότητα των θεμάτων του σεπτεμβρίου 2010;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sakis on June 09, 2011, 01:47:31 am
Αναπολώντας το 4αρι που πήρα το Σεπτέμβρη στο Λογισμό ΙΙ επειδή δεν έπιασα 1,5 μονάδα στα θέματα β ενότητας, και κοιτάζοντας τώρα τις αντίστοιχες λύσεις, μου γεννάται η ανυπέρβλητη επιθυμία να χαστουκίσω τον Κάππο. Ειν' κακό?
+1 κοπηκα γ τον ακριβως ιδιο λογο το σεπτ.κ η μαλακια ειναι πως κανακη πηρα 5,5. αραγε δεν αναρωτιεται ο καρκινιαρης γτ να μην μπορουμε να γραψουμε σε αυτον?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Άδης on June 09, 2011, 01:52:27 am
Αναπολώντας το 4αρι που πήρα το Σεπτέμβρη στο Λογισμό ΙΙ επειδή δεν έπιασα 1,5 μονάδα στα θέματα β ενότητας, και κοιτάζοντας τώρα τις αντίστοιχες λύσεις, μου γεννάται η ανυπέρβλητη επιθυμία να χαστουκίσω τον Κάππο. Ειν' κακό?
+1 κοπηκα γ τον ακριβως ιδιο λογο το σεπτ.κ η μαλακια ειναι πως κανακη πηρα 5,5. αραγε δεν αναρωτιεται ο καρκινιαρης γτ να μην μπορουμε να γραψουμε σε αυτον?
Κι εγώ έτσι κόπηκα. 4.5 στον κανάκη, 1 στον Κάππο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Nerevar on June 09, 2011, 02:00:45 am
Παραθετω και εδω το αντιστοιχο topic για τον λογισμο 2...
https://www.thmmy.gr/smf/index.php?topic=1526.0 (https://www.thmmy.gr/smf/index.php?topic=1526.0) (καπου στη μεση ειναι που μιλαει και ο Καππος)
Εγω παντως τη μια φορα που εδωσα εγραψα 3.5+0 (0 στο κομματι του Καππου εννοειται).
https://www.thmmy.gr/smf/index.php?topic=1526.0 (https://www.thmmy.gr/smf/index.php?topic=1526.0) (καπου στη μεση ειναι που μιλαει και ο Καππος)
Εγω παντως τη μια φορα που εδωσα εγραψα 3.5+0 (0 στο κομματι του Καππου εννοειται).
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on June 10, 2011, 14:26:33 pm
Αναπολώντας το 4αρι που πήρα το Σεπτέμβρη στο Λογισμό ΙΙ επειδή δεν έπιασα 1,5 μονάδα στα θέματα β ενότητας, και κοιτάζοντας τώρα τις αντίστοιχες λύσεις, μου γεννάται η ανυπέρβλητη επιθυμία να χαστουκίσω τον Κάππο. Ειν' κακό?
+1 κοπηκα γ τον ακριβως ιδιο λογο το σεπτ.κ η μαλακια ειναι πως κανακη πηρα 5,5. αραγε δεν αναρωτιεται ο καρκινιαρης γτ να μην μπορουμε να γραψουμε σε αυτον?
Κι εγώ έτσι κόπηκα. 4.5 στον κανάκη, 1 στον Κάππο
Και γω νομίζω τους ίδιους βαθμούς με σένα είχα γράψει. Τουλάχιστον ας έμενε ο βαθμός της μιας ενότητας να δίναμε μόνο την άλλη >:(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: takzago on June 12, 2011, 11:59:42 am
Θέμα 4 Σεπτέμβρης 2010 :
Προσδιορίστε την ελάχιστη τιμή που παίρνει η συνάρτηση w = (1/x +1/y +1/z)
όταν υπολογίζεται πάνω στο επίπεδο x+y+z=c με x,y,z,c >0
Ξέρει κανείς πως λύνεται?
Προσδιορίστε την ελάχιστη τιμή που παίρνει η συνάρτηση w = (1/x +1/y +1/z)
όταν υπολογίζεται πάνω στο επίπεδο x+y+z=c με x,y,z,c >0
Ξέρει κανείς πως λύνεται?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: termi on June 12, 2011, 12:11:38 pm
Θέμα 4 Σεπτέμβρης 2010 :
Προσδιορίστε την ελάχιστη τιμή που παίρνει η συνάρτηση w = (1/x +1/y +1/z)
όταν υπολογίζεται πάνω στο επίπεδο x+y+z=c με x,y,z,c >0
Ξέρει κανείς πως λύνεται?
Προσδιορίστε την ελάχιστη τιμή που παίρνει η συνάρτηση w = (1/x +1/y +1/z)
όταν υπολογίζεται πάνω στο επίπεδο x+y+z=c με x,y,z,c >0
Ξέρει κανείς πως λύνεται?
πορτοκαλί βιβλίο σελίδα 323-324 : Παράδειγμα 3.1!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: takzago on June 12, 2011, 14:22:52 pm
Ευχαριστώ πολύ!
Κι άλλη απορία : Να βρείτε μέγιστα και ελάχιστα της f(x,y)=4x2+10y2 με τη δέσμευση x2 + y2<4
Βρίσκω σημεία πιθανών ακροτάτων (0,2) , (0,-2) , (2,0) , (-2,0) και λ = -4 ή λ =-10 αλλά μετά δεν μπορώ να συνεχίσω γιατί η ορίζουσα του εσσιανού πίνακα βγαίνει μηδέν!
Κι άλλη απορία : Να βρείτε μέγιστα και ελάχιστα της f(x,y)=4x2+10y2 με τη δέσμευση x2 + y2<4
Βρίσκω σημεία πιθανών ακροτάτων (0,2) , (0,-2) , (2,0) , (-2,0) και λ = -4 ή λ =-10 αλλά μετά δεν μπορώ να συνεχίσω γιατί η ορίζουσα του εσσιανού πίνακα βγαίνει μηδέν!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Verminoz on June 12, 2011, 15:08:58 pm
0 γιατί? εμένα μια χαρά μου βγαίνει ο πίνακας...δες πορτοκαλί βιβλίο σελ 326 κάτω. Αυτό τον πίνακα πρέπει να πάρεις.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: takzago on June 12, 2011, 15:39:04 pm
326 σελίδα? Δεν βλέπω πίμνακα εκεί.
Επισυνάπτω τι κάνω μπας και βρείτε τι κάνω λάθος γιατί τα χω παίξει με αυτή την άσκηση...!
Επισυνάπτω τι κάνω μπας και βρείτε τι κάνω λάθος γιατί τα χω παίξει με αυτή την άσκηση...!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: amantziaris on June 12, 2011, 16:31:23 pm
opoios uperoxos sunadelfos exei k mporei as anevasei themata prosfaton eksetastikon.euxaristo polu prokatavolika.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Verminoz on June 12, 2011, 16:56:28 pm
326 σελίδα? Δεν βλέπω πίμνακα εκεί.
Επισυνάπτω τι κάνω μπας και βρείτε τι κάνω λάθος γιατί τα χω παίξει με αυτή την άσκηση...!
Επισυνάπτω τι κάνω μπας και βρείτε τι κάνω λάθος γιατί τα χω παίξει με αυτή την άσκηση...!
Προφανώς έχουμε διαφορετική έκδοση του βιβλίου. Τέλος πάντων ο πίνακας που πρέπει να πάρεις είναι ο Δ1
| Fxx Fxy gx |
| Fxy Fxy gy |
| gx gy 0 |
όπου F = f(x,y) + λg(x,y)
Fxx, Fyy, Fxy προφανώς οι αντίστοιχες παράγωγοι.
Δ1 > 0 --> τοπικό μέγιστο
Δ1 < 0 --> τοπικό ελάχιστο
opoios uperoxos sunadelfos exei k mporei as anevasei themata prosfaton eksetastikon.euxaristo polu prokatavolika.
http://blackboard.lib.auth.gr/webapps/portal/frameset.jsp?tab=courses&url=%2Fbin%2Fcommon%2Fcourse.pl%3Fcourse_id%3D_250_1&
Εδώ έχει θέματα πρόσφατων εξεταστικών μαζί με τις λύσεις τους από αυτά που βάζει ο Κάππος. Επιπλέον εκφωνήσεις υπάρχουν στα Downloads του forum.
https://www.thmmy.gr/smf/index.php?action=tpmod;dl=cat36
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: amantziaris on June 12, 2011, 17:12:38 pm
hmoun sigouros pos tha mou upodeikseis auta pou hdh gnorizo.einai polu liga omos k mono gia dianusmatikh analush.peraitero themata den exei kaneis,? kurios gia to proto kommati tou logismou sunarthseon pollon metavlhton?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Dimitroula on June 13, 2011, 11:53:34 am
Παιδιά, μια χαζή ερώτηση...αλλά οι εκφωνήσεις του Ιουλίου 2009 που βρίσκονται?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Verminoz on June 13, 2011, 12:09:37 pm
Παιδιά, μια χαζή ερώτηση...αλλά οι εκφωνήσεις του Ιουλίου 2009 που βρίσκονται?
https://www.thmmy.gr/smf/index.php?action=tpmod;dl=item1350
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ncr on June 13, 2011, 17:02:24 pm
Στο θέμα 2ο του Σεπτεμβρίου 2010 για να βρω το ολικό διαφορικό dz χρειάζομαι τις μερικές παραγώγους της z=y^(y*(e^x)) ως προς x και ως προς y. Το έχει λύσει κανείς το θέμα; δυσκολεύομαι να βρω τις παραγώγους αυτές..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on June 13, 2011, 17:07:02 pm
Στο θέμα 2ο του Σεπτεμβρίου 2010 για να βρω το ολικό διαφορικό dz χρειάζομαι τις μερικές παραγώγους της z=y^(y*(e^x)) ως προς x και ως προς y. Το έχει λύσει κανείς το θέμα; δυσκολεύομαι να βρω τις παραγώγους αυτές..
χμ... ναι οντως... καποιος?Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: christineL on June 13, 2011, 17:24:25 pm
θετεις u=e^x*y ,παραγωγιζεις μετα ως προσ χ , θετεις u=y kai v=e^x*y ,παραγωγιζεις ως προσ y.Να τα γραψω πιο αναλυτικα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Dimitroula on June 13, 2011, 18:33:59 pm
Παιδιά, κανείς το 3ο του Σεπτέμβρη; Το α ερώτημα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Verminoz on June 13, 2011, 18:44:21 pm
Παιδιά, κανείς το 3ο του Σεπτέμβρη; Το α ερώτημα;
Σεπτέμβρη 2010?
Σειρά Taylor:
f(x,y) = (e/2)*x^2 + (e/2)*y^2 - e*x - (e/2)*π*y + (e/8)*π^2
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: takzago on July 18, 2011, 18:56:04 pm
Mipos mporei kapoios na anevasei ta themata tou Iouniou 2011 na prospathisoume na ta lysoume?
An exei kapoios kai lyseis tha itan akomi kalytera!
An exei kapoios kai lyseis tha itan akomi kalytera!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: antony on August 22, 2011, 17:14:55 pm
Mipos mporei kapoios na anevasei ta themata tou Iouniou 2011 na prospathisoume na ta lysoume?
An exei kapoios kai lyseis tha itan akomi kalytera!
An exei kapoios kai lyseis tha itan akomi kalytera!
όντως αν κάποιος είχε κρατήσει τα θέματα του καλοκαιριού, θα ήταν εξαιρετικό αν τα ανέβαζε.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Emfanever on August 25, 2011, 15:16:53 pm
Mipos mporei kapoios na anevasei ta themata tou Iouniou 2011 na prospathisoume na ta lysoume?
An exei kapoios kai lyseis tha itan akomi kalytera!
An exei kapoios kai lyseis tha itan akomi kalytera!
όντως αν κάποιος είχε κρατήσει τα θέματα του καλοκαιριού, θα ήταν εξαιρετικό αν τα ανέβαζε.
bump
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kargas on August 27, 2011, 17:02:53 pm
Στο θέμα 2ο του Σεπτεμβρίου 2010 για να βρω το ολικό διαφορικό dz χρειάζομαι τις μερικές παραγώγους της z=y^(y*(e^x)) ως προς x και ως προς y. Το έχει λύσει κανείς το θέμα; δυσκολεύομαι να βρω τις παραγώγους αυτές..
edw egw 8elw na rwtisw kati allo...edw to z orizete peplegmena? h paw ntou ston patsa kanonika, exw faei skali twra...
damn it genika gt dn leei f=... kai leei z=... kai mperdeuomai?
telos poso vrikate? ~=3%? h exw kanei mlkies :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on August 27, 2011, 18:22:35 pm
Στο θέμα 2ο του Σεπτεμβρίου 2010 για να βρω το ολικό διαφορικό dz χρειάζομαι τις μερικές παραγώγους της z=y^(y*(e^x)) ως προς x και ως προς y. Το έχει λύσει κανείς το θέμα; δυσκολεύομαι να βρω τις παραγώγους αυτές..
edw egw 8elw na rwtisw kati allo...edw to z orizete peplegmena? h paw ntou ston patsa kanonika, exw faei skali twra...
damn it genika gt dn leei f=... kai leei z=... kai mperdeuomai?
telos poso vrikate? ~=3%? h exw kanei mlkies :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kargas on August 27, 2011, 18:24:05 pm
to elisa san na einai mplegmeni kai vgenei to idio, are ti sou einai ta ma8imatika! :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xarotaki on September 08, 2011, 11:19:22 am
Καλησπέρα!
Ξέρει κανείς πού μπορώ να βρω την εκφώνηση από τα θέματα του Σεπτέμβρη 2008;
Δεν φαίνεται να υπάρχουν στα downloads.
Ξέρει κανείς πού μπορώ να βρω την εκφώνηση από τα θέματα του Σεπτέμβρη 2008;
Δεν φαίνεται να υπάρχουν στα downloads.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nikos912000 on September 08, 2011, 22:55:24 pm
Καλησπέρα!
Ξέρει κανείς πού μπορώ να βρω την εκφώνηση από τα θέματα του Σεπτέμβρη 2008;
Δεν φαίνεται να υπάρχουν στα downloads.
Ξέρει κανείς πού μπορώ να βρω την εκφώνηση από τα θέματα του Σεπτέμβρη 2008;
Δεν φαίνεται να υπάρχουν στα downloads.
Το κομμάτι του Κάππου το έχει στο blackboard με τις λύσεις...
Code:
http://blackboard.lib.auth.gr/@@6B083D7224BFDD1F1CDA1F8B635B4028/courses/1/10U005/content/_93893_1/Logismos2_9_08.pdf
του Κανάκη μάλλον δεν είχαν ανέβει!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xarotaki on September 13, 2011, 15:41:27 pm
Σ' ευχαριστώ πολύ για την απάντηση, :)
Αλλά αυτό το pdf έχει μόνο τις λύσεις, οι εκφωνήσεις από τα θέματα μήπως ξέρεις πού βρίσκονται;
Αλλά αυτό το pdf έχει μόνο τις λύσεις, οι εκφωνήσεις από τα θέματα μήπως ξέρεις πού βρίσκονται;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on September 19, 2011, 17:56:06 pm
Ήμασταν όλοι τόσο απορροφημένοι από τα θέματα, τον Φεβρουάριο, που δεν σκέφτηκε κανείς να τα βγάλει μια φωτογραφία? Και πως γίνεται να κοβόμαστε όλοι τότε...?!?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: antony on September 28, 2011, 15:59:46 pm
Παιδιά επειδή ο λογισμός είναι το τελευταίο μάθημα που μου χει απομείνει για το πτυχίο και δεν έχω κ την καλύτερη ενημέρωση καθώς μπήκα στρατό, μπορεί κάποιος να μου λύσει την παρακάτω απορία?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on September 28, 2011, 17:27:49 pm
Παιδιά επειδή ο λογισμός είναι το τελευταίο μάθημα που μου χει απομείνει για το πτυχίο και δεν έχω κ την καλύτερη ενημέρωση καθώς μπήκα στρατό, μπορεί κάποιος να μου λύσει την παρακάτω απορία?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Έιναι κάτι που θα συζητηθεί μόνο και εφόσον λήξει η κατάληψη.
Εξάλλου ακόμη είσαι στο κέντρο... δεν σου δίνουν άδειες :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: SPRAS on September 28, 2011, 21:36:57 pm
αυτό δεν είναι σίγουρο...εξαρτάται από τον διοικητή...εγώ είχα πάρει στο κέντρο άδεια για μάθημα και χωρίς βύσμα...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: antony on September 28, 2011, 21:43:28 pm
Παιδιά επειδή ο λογισμός είναι το τελευταίο μάθημα που μου χει απομείνει για το πτυχίο και δεν έχω κ την καλύτερη ενημέρωση καθώς μπήκα στρατό, μπορεί κάποιος να μου λύσει την παρακάτω απορία?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Το Σεπτέμβριο γνωρίζω πως δεν υπάρχει πτυχιακή εξεταστική, καθώς όλοι εξεταζόμαστε με τα ίδια θέματα. Σε περίπτωση -που όπως βλέπω εκεί οδηγούμαστε- η εξεταστική χαθεί, υπάρχει περίπτωση να υπάρξει πτυχιακή?
Έιναι κάτι που θα συζητηθεί μόνο και εφόσον λήξει η κατάληψη.
Εξάλλου ακόμη είσαι στο κέντρο... δεν σου δίνουν άδειες :)
σ' ευχαριστώ!
έχω τελειώσει την εκπαίδευση στο κέντρο, μπήκα με την 1η φουρνιά της εσσο σεπτεμβρίου στις 31 αυγούστου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on October 23, 2011, 11:10:10 am
Ένα πεδίο είναι συντηρητικό όταν και μόνο όταν είναι ΑΣΤΡΟΒΙΛΟ και επίσης δεν έχει ΙΔΙΑΖΟΝΤΑ σημεία?
Σωστά?
Σωστά?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: peter_north on October 23, 2011, 11:59:49 am
Και ορίζεται σε απλά συνεκτικό χώρο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on October 23, 2011, 14:30:09 pm
Τι μπορεί να βάλει απο την 1 θεμελιώδη μορφή?
Τι είπε μέσα στα μαθήματα για όποιον παρακολούθησε?
Κάποια tips για λάθη που πρέπει να αποφευχθούν?
Τι είπε μέσα στα μαθήματα για όποιον παρακολούθησε?
Κάποια tips για λάθη που πρέπει να αποφευχθούν?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cyb3rb0ss on February 14, 2012, 22:07:08 pm
Για πείτε για τα θέματα τίποτα...
...μήπως...ΜΗΠΩΣ τα έχει κανείς? φωτό κλπ κλπ?
...μήπως...ΜΗΠΩΣ τα έχει κανείς? φωτό κλπ κλπ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mako54 on February 14, 2012, 22:57:13 pm
Δεν τα έχω σε φώτο, αλλά περιφραστικά είχαν ως εξής:
Στο 1ο ζητούσε i)ουσιαστικά μια απλή εξίσωση εφαπτόμενου επιπέδου,ii)να υπολογίσεις ολικό διαφορικό dz και προσεγγιστική τιμή για την συνάρτηση z=y^cosx. (!)
Στο 2ο θέμα ζητούσε i)σειρά MacLaurin για μια συνάρτηση με υπερβολικό ημίτονο και συνημίτονο, ii)δεσμευμένο ακρότατο σε διατύπωση τύπου "πρόβλημα"
Στο 3ο θέμα ήθελε i)υπολογισμό ενός απλού διπλού ολοκληρώματος σε πολικές συντεταγμένες.
ii)την άσκηση 7 από τις ασκήσεις με τα τριπλά ολοκληρώματα του πορτοκαλί βιβλίου
Όλα τα παραπάνω ήταν η Α ενότητα, τα άλλα ήταν θέματα φιλοσοφίας κ.Κάππου..Αυτά..
Στο 1ο ζητούσε i)ουσιαστικά μια απλή εξίσωση εφαπτόμενου επιπέδου,ii)να υπολογίσεις ολικό διαφορικό dz και προσεγγιστική τιμή για την συνάρτηση z=y^cosx. (!)
Στο 2ο θέμα ζητούσε i)σειρά MacLaurin για μια συνάρτηση με υπερβολικό ημίτονο και συνημίτονο, ii)δεσμευμένο ακρότατο σε διατύπωση τύπου "πρόβλημα"
Στο 3ο θέμα ήθελε i)υπολογισμό ενός απλού διπλού ολοκληρώματος σε πολικές συντεταγμένες.
ii)την άσκηση 7 από τις ασκήσεις με τα τριπλά ολοκληρώματα του πορτοκαλί βιβλίου
Όλα τα παραπάνω ήταν η Α ενότητα, τα άλλα ήταν θέματα φιλοσοφίας κ.Κάππου..Αυτά..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cindy on February 15, 2012, 13:08:16 pm
Μήπως σου έβγαινε ένα άθροισμα κλασμάτων με παρονομαστές τις παραμέτρους στο τετράγωνο..;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: assis on February 15, 2012, 13:20:23 pm
Μήπως σου έβγαινε ένα άθροισμα κλασμάτων με παρονομαστές τις παραμέτρους στο τετράγωνο..;;
Ναι,αλλα οι αριθμητες των κλασματων θετικοι αριθμοι και το αθροισμα 0.
Δηλαδη προεκυπτε αθροισμα 3 θετικων αριθμων ισο με 0...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cindy on February 15, 2012, 16:01:29 pm
και εγώ αυτό έβγαλα...το κοιτούσα ξανά και ξανά αλλά δεν έβρισκα λάθος... :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: assis on February 15, 2012, 16:27:53 pm
και εγώ αυτό έβγαλα...το κοιτούσα ξανά και ξανά αλλά δεν έβρισκα λάθος... :(
το διασταυρωσες με καποιον αλλο?γιατι θεμα λαθους στις παραγωγισεις/πραξεις δεν παιζει...
εκτος και αν χρησιμοποιησαμε λαθος τυπο(?).
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ippocrates9 on August 27, 2012, 11:20:24 am
Υπάρχουν κάπου τα θέματα Ιουνίου 2012? (Όχι της επαναληπτικής)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on August 27, 2012, 13:44:41 pm
κοιτα στο blackboard
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 06, 2012, 15:36:42 pm
Σεπτ. 2010, έχει λύσει κανείς το (α) ερώτημα από 6ο θέμα? Στο (β) βρίσκετε ολες τις περιστροφές των Β1,2,3 μηδέν? Στο (γ) λόγω γραμμικότητας του επικαμπυλίου και με χρήση του Green δεν είναι πάλι μηδέν το ζητούμενο? Πολύ εύκολο για να είναι αληθινό?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 07, 2012, 18:37:37 pm
Ένα πεδίο είναι συντηρητικό όταν και μόνο όταν είναι ΑΣΤΡΟΒΙΛΟ και επίσης δεν έχει ΙΔΙΑΖΟΝΤΑ σημεία?
Σωστά?
Σωστά?
Αν rot=0 παντού στο σύνολο ορισμού, το να μην έχει ιδιάζοντα σημεία γιατί είναι προϋπόθεση ωστέ να είναι συντηρητικό? Από κάππο σελ.48 πρόταση 3.2 δεν συμπαιρένουμε κάτι τέτοιο... Επίσης το ηλεκτρoστατικό πεδίο δεν είναι συντηρητικό? (Δεν ορίζεται στο 0,0,0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: maya_the_bee on September 13, 2012, 23:14:40 pm
Παιδιά μια βοήθεια αν μπορείτε.. Στα θέματα Ιουνίου 2012 (όχι της επαναληπτικής) μπορεί κάποιος να μου εξηγήσει πώς βγαίνει το 1.β?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 15, 2012, 15:42:18 pm
Παιδιά μια βοήθεια αν μπορείτε.. Στα θέματα Ιουνίου 2012 (όχι της επαναληπτικής) μπορεί κάποιος να μου εξηγήσει πώς βγαίνει το 1.β?
Μάγια είναι πολύ απλό, στην ουσία ζητάει το ολικό διαφορικό της συναρτησης για dx=(x-x0)=(1-ε-1) και αντίστοιχα για το dy. Διάβασε τον ορισμό του ολικου διαφορικού και θα καταλάβεις...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 15, 2012, 17:30:29 pm
Ένα πεδίο είναι συντηρητικό όταν και μόνο όταν είναι ΑΣΤΡΟΒΙΛΟ και επίσης δεν έχει ΙΔΙΑΖΟΝΤΑ σημεία?
Σωστά?
Σωστά?
Αν rot=0 παντού στο σύνολο ορισμού, το να μην έχει ιδιάζοντα σημεία γιατί είναι προϋπόθεση ωστέ να είναι συντηρητικό? Από κάππο σελ.48 πρόταση 3.2 δεν συμπαιρένουμε κάτι τέτοιο... Επίσης το ηλεκτρoστατικό πεδίο δεν είναι συντηρητικό? (Δεν ορίζεται στο 0,0,0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: maya_the_bee on September 15, 2012, 17:53:06 pm
Παιδιά μια βοήθεια αν μπορείτε.. Στα θέματα Ιουνίου 2012 (όχι της επαναληπτικής) μπορεί κάποιος να μου εξηγήσει πώς βγαίνει το 1.β?
Μάγια είναι πολύ απλό, στην ουσία ζητάει το ολικό διαφορικό της συναρτησης για dx=(x-x0)=(1-ε-1) και αντίστοιχα για το dy. Διάβασε τον ορισμό του ολικου διαφορικού και θα καταλάβεις...
Σ' ευχαριστώ πολύ! :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 15, 2012, 20:18:26 pm
Ένα πεδίο είναι συντηρητικό όταν και μόνο όταν είναι ΑΣΤΡΟΒΙΛΟ και επίσης δεν έχει ΙΔΙΑΖΟΝΤΑ σημεία?
Σωστά?
Σωστά?
Αν rot=0 παντού στο σύνολο ορισμού, το να μην έχει ιδιάζοντα σημεία γιατί είναι προϋπόθεση ωστέ να είναι συντηρητικό? Από κάππο σελ.48 πρόταση 3.2 δεν συμπαιρένουμε κάτι τέτοιο... Επίσης το ηλεκτρoστατικό πεδίο δεν είναι συντηρητικό? (Δεν ορίζεται στο 0,0,0)
Χωρις να είμαι ουτε για πλάκα ειδήμων, το κεφάλαιο αυτό στο οποίο παραπέμπεις αφορά πεδία στο επιπέδο και όχι στο χωρο. Οπότε σε ξαναστέλνω στον ορισμό σελ. 48 προτ. 3.2.
Επίσης μήπως έχεις δει πρώτο θέμα κάππου από Σεπτ. 2007?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: c0ndemn3d on September 15, 2012, 20:39:52 pm
Το πεδίο μπορεί να μην ορίζεται σε κάποια σημεία (ιδιάζοντα), αλλά και να ορίζεται συνάρτηση δυναμικού για αυτό.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 15, 2012, 20:42:58 pm
Ένα πεδίο είναι συντηρητικό όταν και μόνο όταν είναι ΑΣΤΡΟΒΙΛΟ και επίσης δεν έχει ΙΔΙΑΖΟΝΤΑ σημεία?
Σωστά?
Σωστά?
Αν rot=0 παντού στο σύνολο ορισμού, το να μην έχει ιδιάζοντα σημεία γιατί είναι προϋπόθεση ωστέ να είναι συντηρητικό? Από κάππο σελ.48 πρόταση 3.2 δεν συμπαιρένουμε κάτι τέτοιο... Επίσης το ηλεκτρoστατικό πεδίο δεν είναι συντηρητικό? (Δεν ορίζεται στο 0,0,0)
Χωρις να είμαι ουτε για πλάκα ειδήμων, το κεφάλαιο αυτό στο οποίο παραπέμπεις αφορά πεδία στο επιπέδο και όχι στο χωρο. Οπότε σε ξαναστέλνω στον ορισμό σελ. 48 προτ. 3.2.
Επίσης μήπως έχεις δει πρώτο θέμα κάππου από Σεπτ. 2007?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 15, 2012, 21:23:15 pm
Ευχαριστώ για την υπόδειξη, τόσο καιρό κοιτούσα παλια θέματα και ουτε που ήξερα για τις ασκησεις αυτές. Μήπως μπορείς να καταλάβεις στη συγκεκριμένη άσκηση 14 ποια επιφάνεια παίρνει για να αποδείξει στο τέλος το Stokes?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 15, 2012, 22:14:43 pm
Ευχαριστώ για την υπόδειξη, τόσο καιρό κοιτούσα παλια θέματα και ουτε που ήξερα για τις ασκησεις αυτές. Μήπως μπορείς να καταλάβεις στη συγκεκριμένη άσκηση 14 ποια επιφάνεια παίρνει για να αποδείξει στο τέλος το Stokes?
την ιδια επιφανεια που εδωσε στην αρχη..απλα συμπεραινει οτι η επιφανεια "κινειται"μεταξυ 2 επιπεδων παραλληλων στο χΨ και γι αυτο παιρνει το μοναδιαιο κατα την κατευθυνση του ζTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: COACH on September 15, 2012, 22:38:23 pm
σατανικα πραματα.... αλλα καταλαβα τι λες τελικα...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: maya_the_bee on September 15, 2012, 23:48:31 pm
άλλη μια απορία. Για να βρούμε τον όγκο πως ξέρουμε αν πρέπει να χρησιμοποιήσουμε τριπλό ή διπλό ολοκλήρωμα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 15, 2012, 23:56:34 pm
Ευχαριστώ για την υπόδειξη, τόσο καιρό κοιτούσα παλια θέματα και ουτε που ήξερα για τις ασκησεις αυτές. Μήπως μπορείς να καταλάβεις στη συγκεκριμένη άσκηση 14 ποια επιφάνεια παίρνει για να αποδείξει στο τέλος το Stokes?
την ιδια επιφανεια που εδωσε στην αρχη..απλα συμπεραινει οτι η επιφανεια "κινειται"μεταξυ 2 επιπεδων παραλληλων στο χΨ και γι αυτο παιρνει το μοναδιαιο κατα την κατευθυνση του ζΤο επιφανειακό ολοκλήρωμα το υπολογίζει στο μοναδιαίο κυκλικό δίσκο με προσανατολισμό προς τα θετικά z, amirite?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 16, 2012, 00:02:22 am
άλλη μια απορία. Για να βρούμε τον όγκο πως ξέρουμε αν πρέπει να χρησιμοποιήσουμε τριπλό ή διπλό ολοκλήρωμα?
Χρησιμοποία διπλό. Τεσπα αμα χρησιμοοιήσεις τριπλό απλά μεσα στο ολοκληρωμα θα βαλεις 1.Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: maya_the_bee on September 16, 2012, 00:16:21 am
άλλη μια απορία. Για να βρούμε τον όγκο πως ξέρουμε αν πρέπει να χρησιμοποιήσουμε τριπλό ή διπλό ολοκλήρωμα?
Χρησιμοποία διπλό. Τεσπα αμα χρησιμοοιήσεις τριπλό απλά μεσα στο ολοκληρωμα θα βαλεις 1.οκ ευχαριστώ..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: tomshare3 on September 16, 2012, 00:54:10 am
άλλη μια απορία. Για να βρούμε τον όγκο πως ξέρουμε αν πρέπει να χρησιμοποιήσουμε τριπλό ή διπλό ολοκλήρωμα?
Χρησιμοποία διπλό. Τεσπα αμα χρησιμοοιήσεις τριπλό απλά μεσα στο ολοκληρωμα θα βαλεις 1.αν δοκιμασεις να βρεις τον ιδιο ογκο και με τους δυο τροπους θα δεις οτι ειναι το ιδιο πραγμα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: miaou on September 16, 2012, 02:18:01 am
καλή επιτυχια tomshare3! :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: tomshare3 on September 16, 2012, 02:37:22 am
καλή επιτυχια tomshare3! :)
για σας ειναι η ζωη που ξεμπλεξατε νωρις απο λογισμο!! ;D ;D thx miaou!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 16, 2012, 12:32:10 pm
Ευχαριστώ για την υπόδειξη, τόσο καιρό κοιτούσα παλια θέματα και ουτε που ήξερα για τις ασκησεις αυτές. Μήπως μπορείς να καταλάβεις στη συγκεκριμένη άσκηση 14 ποια επιφάνεια παίρνει για να αποδείξει στο τέλος το Stokes?
την ιδια επιφανεια που εδωσε στην αρχη..απλα συμπεραινει οτι η επιφανεια "κινειται"μεταξυ 2 επιπεδων παραλληλων στο χΨ και γι αυτο παιρνει το μοναδιαιο κατα την κατευθυνση του ζΤο επιφανειακό ολοκλήρωμα το υπολογίζει στο μοναδιαίο κυκλικό δίσκο με προσανατολισμό προς τα θετικά z, amirite?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 16, 2012, 12:54:38 pm
Η επιφάνεια μπορείς να βρεις τι παραμετρική εξίσωση έχει?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 16, 2012, 13:16:37 pm
Η επιφάνεια μπορείς να βρεις τι παραμετρική εξίσωση έχει?
παρε κυλινδρικες συντεταγμενες για τον κυλινδρο αλλα αντι για ζ=ζ βαλε ζ=χ^2-ψ^2=(ρ*συνθ)^2-(ρ*ημθ)^2=ρ^2*συν(2*θ)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: teslaaaa on September 16, 2012, 13:21:04 pm
οταν θελουμε να βρουμε διανυσματικο πεδιο καθετο σε μια επιφανεια θελουμε να βρουμε Φ τετοιο ωστε ροτ(Φ)*η=0? οπου η το καθετο στην επιφανεια διανυσμα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 16, 2012, 13:34:12 pm
Η επιφάνεια μπορείς να βρεις τι παραμετρική εξίσωση έχει?
παρε κυλινδρικες συντεταγμενες για τον κυλινδρο αλλα αντι για ζ=ζ βαλε ζ=χ^2-ψ^2=(ρ*συνθ)^2-(ρ*ημθ)^2=ρ^2*συν(2*θ)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 16, 2012, 13:37:40 pm
οταν θελουμε να βρουμε διανυσματικο πεδιο καθετο σε μια επιφανεια θελουμε να βρουμε Φ τετοιο ωστε ροτ(Φ)*η=0? οπου η το καθετο στην επιφανεια διανυσμα
Όταν θέλουμε πεδίο κάθετο σε επιφάνεια πρέπει Φ*Ru=0 και Φ*Rv=0 όπου Ru,Rv τα εφαπτόμενα διανύσματα της επιφάνειας.Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konstantia on September 16, 2012, 15:28:16 pm
Μπορεί κάποιος να μου πει τι πρέπει να κάνω στο πρώτο θέμα της επαναληπτικής εξέτασης τον Ιούνιο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 16:07:26 pm
στο διαφορικο, στο taylor η στη θερμοκρασια;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 16:08:35 pm
η απαντηση ειναι, διαφορικο 1-2-3ης ταξης, αναπτυγμα taylor και κατευθυνομενη παραγωγος... :Ρ
Υ.Γ. Σορρυ για το διπλο ποστ, αν μπορει καποιος να κανει merge :)
Υ.Γ. Σορρυ για το διπλο ποστ, αν μπορει καποιος να κανει merge :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konstantia on September 16, 2012, 16:17:45 pm
η απαντηση ειναι, διαφορικο 1-2-3ης ταξης, αναπτυγμα taylor και κατευθυνομενη παραγωγος... :Ρ
Υ.Γ. Σορρυ για το διπλο ποστ, αν μπορει καποιος να κανει merge :)
Υ.Γ. Σορρυ για το διπλο ποστ, αν μπορει καποιος να κανει merge :)
το διαφορικό με προβλημάτιζε γιατί νόμιζα ότι δεν ορίζονται στο (1,-1) οι μερικές παράγωγοι...αυτά παθαίνει κανείς αν ξυπνάει στις 5.30...σε ευχαριστώ πολύ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 16:21:13 pm
τπτ μαν, καλη μας τυχη. ;) Παντως τα θεματα του ιουνιου καλυτερα μην τα κοιτας, ηταν υπερβολικα γελοια. δεν πεφτουν τετοια επι καππου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konstantia on September 16, 2012, 16:25:28 pm
τπτ μαν, καλη μας τυχη. ;) Παντως τα θεματα του ιουνιου καλυτερα μην τα κοιτας, ηταν υπερβολικα γελοια. δεν πεφτουν τετοια επι καππου.
κοιτάω να δω τι βάζει ο ατρέας...για τον κάππο δεν σχολίαζω... >:(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 16:27:33 pm
80-90% θα βαλει και πλεγμενες συναρτησεις. καλο ειναι να τους ριξεις μια ματια
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konstantia on September 16, 2012, 16:29:58 pm
80-90% θα βαλει και πλεγμενες συναρτησεις. καλο ειναι να τους ριξεις μια ματια
thanks!Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: T--hmmy on September 16, 2012, 16:40:13 pm
τπτ μαν, καλη μας τυχη. ;) Παντως τα θεματα του ιουνιου καλυτερα μην τα κοιτας, ηταν υπερβολικα γελοια. δεν πεφτουν τετοια επι καππου.
καθόλου γελοία! 3 ώρες γράψιμο μέχρι το τελευταίο λεπτό και μέσος χρόνος σκέψης για κάθε άσκηση 2-3 λεπτά..Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 16:44:05 pm
τπτ μαν, καλη μας τυχη. ;) Παντως τα θεματα του ιουνιου καλυτερα μην τα κοιτας, ηταν υπερβολικα γελοια. δεν πεφτουν τετοια επι καππου.
καθόλου γελοία! 3 ώρες γράψιμο μέχρι το τελευταίο λεπτό και μέσος χρόνος σκέψης για κάθε άσκηση 2-3 λεπτά..Ναι ρε φίλε αλλά ήταν βατά! Μπροστά σε αυτά που ζητάει ο Κάππος ήταν απλά μια δύσκολη εξέταση όπως όλες οι υπόλοιπες εξετάσεις παραδοσιακά δύσκολων μαθημάτων στη σχολή.
Τέλος πάντων, προσωπικά ξέμπλεξα με το Λογισμό 2 με την επαναληπτική και αμέσως αισθάνθηκα εκθετικά πιο κοντά στο πτυχίο. Καλή τύχη σε όλους σας εύχομαι.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 16:57:45 pm
τπτ μαν, καλη μας τυχη. ;) Παντως τα θεματα του ιουνιου καλυτερα μην τα κοιτας, ηταν υπερβολικα γελοια. δεν πεφτουν τετοια επι καππου.
καθόλου γελοία! 3 ώρες γράψιμο μέχρι το τελευταίο λεπτό και μέσος χρόνος σκέψης για κάθε άσκηση 2-3 λεπτά..Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 17:06:41 pm
Είσαι μάλλον από τους λίγους προικισμένους ανθρώπους που "το 'χουν" με τα μαθηματικά. Θα σου άξιζε λοιπόν και ένας πολύ καλός βαθμός σε αυτά τα μαθήματα. Όλοι έχουμε κάποιες κλίσεις σε κάποια θέματα παραπάνω από ότι σε άλλα. Αυτό δε σημαίνει ότι τα θέματα ήταν γελοία. Κατά τη γνώμη μου, αυτό θα έπρεπε να είναι το επίπεδο γενικά. Να πάρεις και συ τη βαθμάρα σου που το ΄χεις, να πάρω και γω το 5 μου που ξεσκίζομαι και θέλω απλά να ξεμπερδεύω.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cindy on September 16, 2012, 17:10:34 pm
τ
Τέλος πάντων, προσωπικά ξέμπλεξα με το Λογισμό 2 με την επαναληπτική και αμέσως αισθάνθηκα εκθετικά πιο κοντά στο πτυχίο.
Τέλος πάντων, προσωπικά ξέμπλεξα με το Λογισμό 2 με την επαναληπτική και αμέσως αισθάνθηκα εκθετικά πιο κοντά στο πτυχίο.
+1
^peace^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 17:19:36 pm
Είσαι μάλλον από τους λίγους προικισμένους ανθρώπους που "το 'χουν" με τα μαθηματικά. Θα σου άξιζε λοιπόν και ένας πολύ καλός βαθμός σε αυτά τα μαθήματα. Όλοι έχουμε κάποιες κλίσεις σε κάποια θέματα παραπάνω από ότι σε άλλα. Αυτό δε σημαίνει ότι τα θέματα ήταν γελοία. Κατά τη γνώμη μου, αυτό θα έπρεπε να είναι το επίπεδο γενικά. Να πάρεις και συ τη βαθμάρα σου που το ΄χεις, να πάρω και γω το 5 μου που ξεσκίζομαι και θέλω απλά να ξεμπερδεύω.
Τρελε, κανεις λαθος, στη σχολη μπηκα για τους υπολογιστες και τον ηλεκτρομαγνητισμο, οχι για τα μαθηματικα(αν και μου αρεσουν και αυτα, χωρις να αυνανιζομαι μαζι τους βεβαια). Αντικειμενικα, εξακολουθώ να θεωρω τα θέματα αυτα γελοια και, κατα τη ταπεινη γνώμη μου, κάποιος που δεν πέρασε είτε ήταν πολύ άτυχος είτε δεν έκανε σωστό διάβασμα. Και δεν ειμαι ουτε πιο έξυπνος ούτε καλύτερος στα μαθηματικά σε σχεση με τον μεσο ορο της σχολης. Επετρεψε μου να διαφωνήσω και να συνεχισω να πιστευω πως έχω πολλές πιθανοτητες να κοπω, και οχι να παρω βαθμο σε αυτην την εξεταστικη παροτι πιστευω πως ειμαι ΠΟΛΥ καλα διαβασμένος και έχω κατανοησει εξισου καλα το μαθημα. Ειμαι 99% σιγουρος πως ο καππος θα εχει εμπνευση. Peace.Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 18:04:43 pm
Ίσως να είναι και έτσι όπως τα λες.
Τεσπά, εγώ από τότε που μπήκα σε αυτή τη σχολή άλλαξα ριζικά σχέση με τα μαθηματικά. Από εκεί που τα λάτρευα και τα σκεφτόμουν στο δρόμο ενώ περπατούσα τα σιχάθηκε η ψυχή μου. Λίγο η δυσκολία τους, λίγο ο τρόπος που διδάσκονται, λίγο η αντιμετώπιση από τους καθηγητές του γενικού που τα διδάσκουν με έκανε να τα σιχαθώ. Θυμάμαι από το πρώτο έτος εμάς τους 350 φοιτητές στην αίθουσα 5 και τους καθηγητές να μας αντιμετωπίζουν σαν να είμαστε απόκληροι της κοινωνίας λες και φταίγαμε εμείς που μας βάλανε 18 χρονώ με τα μυαλά στα κάγκελα να κρεμόμαστε από τα φωτιστικά για μια θέση στον ήλιο. Από τότε έχω πάθει κοκομπλόκο με αυτά τα μαθήματα και κάθε φορά που τα πιάνω για να τα περάσω, ένα ένα τη φορά, αισθάνομαι μια αηδία και το βλέπω σαν αγγαρεία και όχι σαν μαθήματα που το καθένα έχει να μου προσφέρει κάτι. Δε νομίζω ότι φταίω μόνο εγώ γι' αυτό που έχω πάθει και εγώ και πολλοί της σειράς μου.
Όσο για τα θέματα συμφωνώ ότι θα υπάρξει έμπνευση. Τι διάολο, τελευταία του εξέταση Λογισμό 2 θα είναι, να μη κάνει φαντασμαγορική έξοδο; Αν και ακόμη κρατάω μικρό καλάθι. Έχουν δει πολλά τα μάτια μου μέσα σε αυτή τη σχολή και αν δε τα δω τα μαθήματα να αλλάζουν χέρια δε πιστεύω τίποτα. Θα δούμε τον Οκτώβριο με τα Εφαρμοσμένα αν ισχύουν όσα λέγονται.
Τεσπά, εγώ από τότε που μπήκα σε αυτή τη σχολή άλλαξα ριζικά σχέση με τα μαθηματικά. Από εκεί που τα λάτρευα και τα σκεφτόμουν στο δρόμο ενώ περπατούσα τα σιχάθηκε η ψυχή μου. Λίγο η δυσκολία τους, λίγο ο τρόπος που διδάσκονται, λίγο η αντιμετώπιση από τους καθηγητές του γενικού που τα διδάσκουν με έκανε να τα σιχαθώ. Θυμάμαι από το πρώτο έτος εμάς τους 350 φοιτητές στην αίθουσα 5 και τους καθηγητές να μας αντιμετωπίζουν σαν να είμαστε απόκληροι της κοινωνίας λες και φταίγαμε εμείς που μας βάλανε 18 χρονώ με τα μυαλά στα κάγκελα να κρεμόμαστε από τα φωτιστικά για μια θέση στον ήλιο. Από τότε έχω πάθει κοκομπλόκο με αυτά τα μαθήματα και κάθε φορά που τα πιάνω για να τα περάσω, ένα ένα τη φορά, αισθάνομαι μια αηδία και το βλέπω σαν αγγαρεία και όχι σαν μαθήματα που το καθένα έχει να μου προσφέρει κάτι. Δε νομίζω ότι φταίω μόνο εγώ γι' αυτό που έχω πάθει και εγώ και πολλοί της σειράς μου.
Όσο για τα θέματα συμφωνώ ότι θα υπάρξει έμπνευση. Τι διάολο, τελευταία του εξέταση Λογισμό 2 θα είναι, να μη κάνει φαντασμαγορική έξοδο; Αν και ακόμη κρατάω μικρό καλάθι. Έχουν δει πολλά τα μάτια μου μέσα σε αυτή τη σχολή και αν δε τα δω τα μαθήματα να αλλάζουν χέρια δε πιστεύω τίποτα. Θα δούμε τον Οκτώβριο με τα Εφαρμοσμένα αν ισχύουν όσα λέγονται.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: COACH on September 16, 2012, 18:45:04 pm
Ίσως να είναι και έτσι όπως τα λες.
Τεσπά, εγώ από τότε που μπήκα σε αυτή τη σχολή άλλαξα ριζικά σχέση με τα μαθηματικά. Από εκεί που τα λάτρευα και τα σκεφτόμουν στο δρόμο ενώ περπατούσα τα σιχάθηκε η ψυχή μου. Λίγο η δυσκολία τους, λίγο ο τρόπος που διδάσκονται, λίγο η αντιμετώπιση από τους καθηγητές του γενικού που τα διδάσκουν με έκανε να τα σιχαθώ. Θυμάμαι από το πρώτο έτος εμάς τους 350 φοιτητές στην αίθουσα 5 και τους καθηγητές να μας αντιμετωπίζουν σαν να είμαστε απόκληροι της κοινωνίας λες και φταίγαμε εμείς που μας βάλανε 18 χρονώ με τα μυαλά στα κάγκελα να κρεμόμαστε από τα φωτιστικά για μια θέση στον ήλιο. Από τότε έχω πάθει κοκομπλόκο με αυτά τα μαθήματα και κάθε φορά που τα πιάνω για να τα περάσω, ένα ένα τη φορά, αισθάνομαι μια αηδία και το βλέπω σαν αγγαρεία και όχι σαν μαθήματα που το καθένα έχει να μου προσφέρει κάτι. Δε νομίζω ότι φταίω μόνο εγώ γι' αυτό που έχω πάθει και εγώ και πολλοί της σειράς μου.
Όσο για τα θέματα συμφωνώ ότι θα υπάρξει έμπνευση. Τι διάολο, τελευταία του εξέταση Λογισμό 2 θα είναι, να μη κάνει φαντασμαγορική έξοδο; Αν και ακόμη κρατάω μικρό καλάθι. Έχουν δει πολλά τα μάτια μου μέσα σε αυτή τη σχολή και αν δε τα δω τα μαθήματα να αλλάζουν χέρια δε πιστεύω τίποτα. Θα δούμε τον Οκτώβριο με τα Εφαρμοσμένα αν ισχύουν όσα λέγονται.
Τεσπά, εγώ από τότε που μπήκα σε αυτή τη σχολή άλλαξα ριζικά σχέση με τα μαθηματικά. Από εκεί που τα λάτρευα και τα σκεφτόμουν στο δρόμο ενώ περπατούσα τα σιχάθηκε η ψυχή μου. Λίγο η δυσκολία τους, λίγο ο τρόπος που διδάσκονται, λίγο η αντιμετώπιση από τους καθηγητές του γενικού που τα διδάσκουν με έκανε να τα σιχαθώ. Θυμάμαι από το πρώτο έτος εμάς τους 350 φοιτητές στην αίθουσα 5 και τους καθηγητές να μας αντιμετωπίζουν σαν να είμαστε απόκληροι της κοινωνίας λες και φταίγαμε εμείς που μας βάλανε 18 χρονώ με τα μυαλά στα κάγκελα να κρεμόμαστε από τα φωτιστικά για μια θέση στον ήλιο. Από τότε έχω πάθει κοκομπλόκο με αυτά τα μαθήματα και κάθε φορά που τα πιάνω για να τα περάσω, ένα ένα τη φορά, αισθάνομαι μια αηδία και το βλέπω σαν αγγαρεία και όχι σαν μαθήματα που το καθένα έχει να μου προσφέρει κάτι. Δε νομίζω ότι φταίω μόνο εγώ γι' αυτό που έχω πάθει και εγώ και πολλοί της σειράς μου.
Όσο για τα θέματα συμφωνώ ότι θα υπάρξει έμπνευση. Τι διάολο, τελευταία του εξέταση Λογισμό 2 θα είναι, να μη κάνει φαντασμαγορική έξοδο; Αν και ακόμη κρατάω μικρό καλάθι. Έχουν δει πολλά τα μάτια μου μέσα σε αυτή τη σχολή και αν δε τα δω τα μαθήματα να αλλάζουν χέρια δε πιστεύω τίποτα. Θα δούμε τον Οκτώβριο με τα Εφαρμοσμένα αν ισχύουν όσα λέγονται.
+1 (σα παλιος και γω...)
για αυριο βαση παλιων θεματων ειναι η πρωτη φορα που δε διαβασα καθολου απο το μπλε παρα μονο του Καππου...
τι λεγεται για τα εφαρμοσμενα btw??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 18:48:46 pm
Και για τα εφαρμοσμένα και για το λογισμο 2 λένε θα τα πάρουν άλλοι καθηγητές. Απλά για το λογισμό δε θα μάθουμε μέχρι το Φλεβάρη. Για τα εφαρμοσμένα θα μάθουμε με το που θα αρχίσει η νέα ακαδημαϊκή χρονιά όμως.
Η λογική λέει ότι εάν ισχύσει αυτό που λέγεται ότι αποφασίστηκε για τα εφαρμοσμένα μάλλον θα ισχύσει και για το άλλο. Το θέμα είναι
- όντως αποφασίστηκε ή είναι ράδιο αρβύλα (η χελώνα είπε ότι αποφασίστηκε και δεν έχω λόγο να μην την πιστέψω).
- ακόμη κι αν αποφασίστηκε θα γίνει ή ήταν τρικ για να εκτονωθεί η συσσωρευμένη οργή;
Με όσα έχω δει στη σχολή αυτή δεν έχω καμία εμπιστοσύνη μέχρι να δω να γίνεται κάτι.
Η λογική λέει ότι εάν ισχύσει αυτό που λέγεται ότι αποφασίστηκε για τα εφαρμοσμένα μάλλον θα ισχύσει και για το άλλο. Το θέμα είναι
- όντως αποφασίστηκε ή είναι ράδιο αρβύλα (η χελώνα είπε ότι αποφασίστηκε και δεν έχω λόγο να μην την πιστέψω).
- ακόμη κι αν αποφασίστηκε θα γίνει ή ήταν τρικ για να εκτονωθεί η συσσωρευμένη οργή;
Με όσα έχω δει στη σχολή αυτή δεν έχω καμία εμπιστοσύνη μέχρι να δω να γίνεται κάτι.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Jim D. Ace on September 16, 2012, 18:51:49 pm
απ οσο ξερω εφαρμοσμενα ατρεας
λογισμος 2 ξενος και ροθος
λογισμος 2 ξενος και ροθος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 18:55:29 pm
Αν δε δω δε πιστεύω...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: COACH on September 16, 2012, 18:57:21 pm
αν το πε η χελωνα εγω ειμαι καλυμμενος. ξενος σημαινει ψιλοστανταρ θεματα απο το μπλε βιβλιο..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 18:58:59 pm
Βρε σου λέω, το ότι αποφασίστηκε δε το αμφισβητώ. Το ότι θα εφαρμοστεί όμως κρατάω τις επιφυλάξεις μου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Jim D. Ace on September 16, 2012, 19:03:03 pm
αν το πε η χελωνα εγω ειμαι καλυμμενος. ξενος σημαινει ψιλοστανταρ θεματα απο το μπλε βιβλιο..
οντως η χελωνα το πεκαι επισης ο καππος θα παρει τις διαφορικες
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 16, 2012, 19:13:36 pm
Έχει κανείς αποτελέσματα απο 1ο θέμα κάππου απο Φεβρ. 2012?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: manina on September 16, 2012, 19:20:29 pm
Παδιά, να κάνω κι εγώ μια ερώτηση, γενικής φύσεως...
Όταν κάνω μετατροπή σε πολικές, το όριο του ολοκληρώματος για το θ πως καταλαβαίνω αν θα το πάρω από 0 εώς 2π ή από -π εώς π ή από -π/2 εώς π/2? Έχω δει και περίπτωση που το παίρνει από 0 εώς π/2.
Έχω μια υποψία στο μυαλό μου, αλλά μπορεί να μου το εξηγήσει κάποιος απλά?
Όταν κάνω μετατροπή σε πολικές, το όριο του ολοκληρώματος για το θ πως καταλαβαίνω αν θα το πάρω από 0 εώς 2π ή από -π εώς π ή από -π/2 εώς π/2? Έχω δει και περίπτωση που το παίρνει από 0 εώς π/2.
Έχω μια υποψία στο μυαλό μου, αλλά μπορεί να μου το εξηγήσει κάποιος απλά?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bakeneko on September 16, 2012, 19:26:38 pm
Εγώ μυρίζω τα νύχια μου πάντως :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Mr K on September 16, 2012, 19:26:54 pm
απο την στιγμη που παιρνεις μια διασταση να την αφαιρεις για να μην μπερδεύεσαι. Θα προβάλεις το τρισδιάστατο σχήμα στο δισδιάστατο επίπεδο και εκεί θα βλέπεις τα όρια της γωνίας (το λέω μπερδεμένα αλλά δεν βρίσκω άλλο τρόπο)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: drosostalithras on September 16, 2012, 19:29:13 pm
Είσαι μάλλον από τους λίγους προικισμένους ανθρώπους που "το 'χουν" με τα μαθηματικά. Θα σου άξιζε λοιπόν και ένας πολύ καλός βαθμός σε αυτά τα μαθήματα. Όλοι έχουμε κάποιες κλίσεις σε κάποια θέματα παραπάνω από ότι σε άλλα. Αυτό δε σημαίνει ότι τα θέματα ήταν γελοία. Κατά τη γνώμη μου, αυτό θα έπρεπε να είναι το επίπεδο γενικά. Να πάρεις και συ τη βαθμάρα σου που το ΄χεις, να πάρω και γω το 5 μου που ξεσκίζομαι και θέλω απλά να ξεμπερδεύω.
Τρελε, κανεις λαθος, στη σχολη μπηκα για τους υπολογιστες και τον ηλεκτρομαγνητισμο, οχι για τα μαθηματικα(αν και μου αρεσουν και αυτα, χωρις να αυνανιζομαι μαζι τους βεβαια). Αντικειμενικα, εξακολουθώ να θεωρω τα θέματα αυτα γελοια και, κατα τη ταπεινη γνώμη μου, κάποιος που δεν πέρασε είτε ήταν πολύ άτυχος είτε δεν έκανε σωστό διάβασμα. Και δεν ειμαι ουτε πιο έξυπνος ούτε καλύτερος στα μαθηματικά σε σχεση με τον μεσο ορο της σχολης. Επετρεψε μου να διαφωνήσω και να συνεχισω να πιστευω πως έχω πολλές πιθανοτητες να κοπω, και οχι να παρω βαθμο σε αυτην την εξεταστικη παροτι πιστευω πως ειμαι ΠΟΛΥ καλα διαβασμένος και έχω κατανοησει εξισου καλα το μαθημα. Ειμαι 99% σιγουρος πως ο καππος θα εχει εμπνευση. Peace.εχει γινει γτπ το γενικο τμημα μονο και μονο απο το γεγονος οτι δεν μπορεις να περασεις το μαθημα που πρεπει να σου μαθει να χρησιμοποιεις ενα εργαλειο, ενω με ανεση περνας τα μαθηματα που το χρησιμοποιουν.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MaGill on September 16, 2012, 19:29:33 pm
Μανίνα το να πάρεις (0,2π) είναι το ίδιο με το να πάρεις (-π,π). Έχει να κάνει με το χωρίο ολοκλήρωσης. Αν ολοκληρώσεις απο -π/2 εως π/2 σημαίνει οτι ο τοπος ολοκλήρωσης είναι το 1ο και 4ο τεταρτημόριο. Απο 0 ως π/2 είναι το 1ο τεταρτημόριο. Ελπίζω να με πιάνεις.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabylonX on September 16, 2012, 19:31:24 pm
Εξαρτάται καθαρά από το σχήμα και πως είναι τοποθετημένο στο χώρο. Αμα δε το σχηματίσεις στο χαρτί συνήθως δε καταλαβαίνεις. Σε διπλό ολοκλήρωμα γίνεται σχετικά εύκολα.
Εάν πχ έχεις διπλό ολοκληρωμα και έχεις το πρώτο τεταρτημόριο ενός κύκλου ακτινας 1 με όρια από 0 έως 1 και 0 εως ρίζα(1-x^2) αυτό για να το μετατρέψεις σε πολικές θα πάει με ορια 0 έως 1 για την ακτίνα και 0 έως π/2 για τη γωνία.
Δεν υπάρχει στανταρ νόρμα. Όπως ορίζονται από τον τόπο ολοκλήρωσης.
Σε τριπλά ολοκληρώματα είναι σχετικά δύσκολο και να ελπίζεις να πέσει απο καρτεσιανές σε κυλινδρικές όπου ο z μένει z και χρειάζεται μόνο μετατροπή μόνο των άλλων δύο διαστάσεων όπως παραπάνω.
Εάν πχ έχεις διπλό ολοκληρωμα και έχεις το πρώτο τεταρτημόριο ενός κύκλου ακτινας 1 με όρια από 0 έως 1 και 0 εως ρίζα(1-x^2) αυτό για να το μετατρέψεις σε πολικές θα πάει με ορια 0 έως 1 για την ακτίνα και 0 έως π/2 για τη γωνία.
Δεν υπάρχει στανταρ νόρμα. Όπως ορίζονται από τον τόπο ολοκλήρωσης.
Σε τριπλά ολοκληρώματα είναι σχετικά δύσκολο και να ελπίζεις να πέσει απο καρτεσιανές σε κυλινδρικές όπου ο z μένει z και χρειάζεται μόνο μετατροπή μόνο των άλλων δύο διαστάσεων όπως παραπάνω.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 20:25:04 pm
Αν παραμεινει ο καππος θα ριξω τρελο γελιο... και κλαμα... :Ρ Damn it, θελω να περασω!
Παδιά, να κάνω κι εγώ μια ερώτηση, γενικής φύσεως...
Όταν κάνω μετατροπή σε πολικές, το όριο του ολοκληρώματος για το θ πως καταλαβαίνω αν θα το πάρω από 0 εώς 2π ή από -π εώς π ή από -π/2 εώς π/2? Έχω δει και περίπτωση που το παίρνει από 0 εώς π/2.
Έχω μια υποψία στο μυαλό μου, αλλά μπορεί να μου το εξηγήσει κάποιος απλά?
Το βλεπεις απο το σχημα, δλδ απο που μέχρι που κυμαινεται η γωνια. 0-2π και (-π)-π ειναι το ιδιο πραμα. (-π/2)-π/2 ειναι ο μισος κυκλος στη μερια του 0χ αξονα. Αν φυσικα χ=ρσυνθ.Όταν κάνω μετατροπή σε πολικές, το όριο του ολοκληρώματος για το θ πως καταλαβαίνω αν θα το πάρω από 0 εώς 2π ή από -π εώς π ή από -π/2 εώς π/2? Έχω δει και περίπτωση που το παίρνει από 0 εώς π/2.
Έχω μια υποψία στο μυαλό μου, αλλά μπορεί να μου το εξηγήσει κάποιος απλά?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: TrueForce on September 16, 2012, 20:29:22 pm
Σε τριπλά ολοκληρώματα είναι σχετικά δύσκολο και να ελπίζεις να πέσει απο καρτεσιανές σε κυλινδρικές όπου ο z μένει z και χρειάζεται μόνο μετατροπή μόνο των άλλων δύο διαστάσεων όπως παραπάνω.
Βασικα εξαρταται απο το σχημα οπως ειπε ο ΒabylonΧ. Αλλοτε βολευει σε πολικες-κυλινδρικες και αλλοτε σε σφαιρικες. Οι σφαιρικες ειναι πανευκολες αν καταλαβεις τις γωνιες. Μονο σε κανεναν κωνο μπορει να σου φανουν λιγο περιεργα τα ορια της ακτινας, αλλα αν κανεις αντικατασταση στις σχεσεις του κωνου θα δεις οτι βγαινει(π.χ. ρ= 0 εως ρσυνφ ). Γενικα να προσεσεις τους κωνους σε σφαιρικες.Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: manina on September 16, 2012, 21:24:54 pm
Ουάου! Πολλές απαντήσεις, σας ευχαριστώ!. Χμ, οκ, δηλαδή πρέπει να το μελετώ κάθε φορά. Είχα πρόβλημα στην άσκηση 12 από τις λυμένες του Ατρέα στο κεφάλαιο 4. Ήταν ένας κύκλος, με κέντρο (1/2, 0) και πήρα το όριο από -π εώς π, και φυσικά μου βγήκε 0 το ολοκλήρωμα, έπρεπε να πάρω -π/2 εώς π/2.
Τεσπά, ο θεός βοηθός εκείνη τη στιγμή.
Τρου φορς, δεν νομίζω να μπορέσω να αναγνωρίσω καν τον κώνο, επομένως δεν θα έχω αμφιβολία καμία.... ;)
Τεσπά, ο θεός βοηθός εκείνη τη στιγμή.
Τρου φορς, δεν νομίζω να μπορέσω να αναγνωρίσω καν τον κώνο, επομένως δεν θα έχω αμφιβολία καμία.... ;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: anrim27 on April 20, 2013, 19:07:37 pm
Ρε παιδια, μπορει να βοηθησει καποιος στο θεμα
θεμα 2,ομαδα Α,πολιτικων μηχανικων,27-8-2007
Εν ολιγοις, μας λεει οτι δινεται z=e-y *f,
η f ειναι συναρτηση του x-y
και ζητειται να αποδειξουμε οτι zx+zxx+zxy=0
θεμα 2,ομαδα Α,πολιτικων μηχανικων,27-8-2007
Εν ολιγοις, μας λεει οτι δινεται z=e-y *f,
η f ειναι συναρτηση του x-y
και ζητειται να αποδειξουμε οτι zx+zxx+zxy=0
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: anrim27 on April 20, 2013, 19:29:13 pm
Τελικα, το βρηκα.
Μπερδευομουν λιγο με τους ορους που προεκυπταν απο την παραγωγιση αλλα,ενταξει.
Μπερδευομουν λιγο με τους ορους που προεκυπταν απο την παραγωγιση αλλα,ενταξει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Μουργόλυκος on April 20, 2013, 20:23:55 pm
Τελικα, το βρηκα.
Μπερδευομουν λιγο με τους ορους που προεκυπταν απο την παραγωγιση αλλα,ενταξει.
Πες πως το έκανες γιατί και εγώ δε μπορώ...Μπερδευομουν λιγο με τους ορους που προεκυπταν απο την παραγωγιση αλλα,ενταξει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: anrim27 on April 20, 2013, 22:27:12 pm
Λογικα,θα ειναι σωστο...
(http://imageshack.us/a/img826/3627/img20130420221834.th.jpg) (http://imageshack.us/photo/my-images/826/img20130420221834.jpg/)
(http://imageshack.us/a/img826/3627/img20130420221834.th.jpg) (http://imageshack.us/photo/my-images/826/img20130420221834.jpg/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Μουργόλυκος on April 20, 2013, 22:33:54 pm
Λογικα,θα ειναι σωστο...
(http://imageshack.us/a/img826/3627/img20130420221834.th.jpg) (http://imageshack.us/photo/my-images/826/img20130420221834.jpg/)
κάτσε αφού η f είναι συνάρτηση του x-y τότε έχουμε σύνθετη παραγώγιση και άρα df/dx=fx*d(x-y)/dx=fx*1(http://imageshack.us/a/img826/3627/img20130420221834.th.jpg) (http://imageshack.us/photo/my-images/826/img20130420221834.jpg/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: anrim27 on April 20, 2013, 22:53:12 pm
Η πρωτη ισοτητα,που δειχνεις,μαλλον δεν ισχυει.
Αυτο που λες ειναι,
η παραγωγος της f ως προς x (στο πρωτο μελος της ισοτητας) ισουται με την παραγωγο της f ως προς x (ενω θα επρεπε να ειναι παραγωγος της f ως προς x-y)επι d(x-y)/d(x).
Νομιζω δηλαδη,δεν ειμαι και πολυ σιγουρος...
Αυτο που λες ειναι,
η παραγωγος της f ως προς x (στο πρωτο μελος της ισοτητας) ισουται με την παραγωγο της f ως προς x (ενω θα επρεπε να ειναι παραγωγος της f ως προς x-y)επι d(x-y)/d(x).
Νομιζω δηλαδη,δεν ειμαι και πολυ σιγουρος...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: RFed the King on April 26, 2013, 01:32:09 am
Πόσο βγαίνει το ολοκλήρωμα θέμα 3 Ιούνιος 2012?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: antonios on April 26, 2013, 01:51:32 am
Πόσο βγαίνει το ολοκλήρωμα θέμα 3 Ιούνιος 2012?
π/6Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on June 22, 2013, 14:26:12 pm
Αν έχει κάποιος τα θέματα των προόδων θα μπορούσε να τα ανεβάσει? Ειδικά αν έχει του Ξένου
(https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ2ePmZx34JNDYlH8AI8bN91sFRkM2e-ZrmSU1hsJSKaA8vh0H3tg)
(https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ2ePmZx34JNDYlH8AI8bN91sFRkM2e-ZrmSU1hsJSKaA8vh0H3tg)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Rocket on June 25, 2013, 11:01:07 am
Αν έχει κάποιος τα θέματα των προόδων θα μπορούσε να τα ανεβάσει? Ειδικά αν έχει του Ξένου
(https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ2ePmZx34JNDYlH8AI8bN91sFRkM2e-ZrmSU1hsJSKaA8vh0H3tg)
(https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ2ePmZx34JNDYlH8AI8bN91sFRkM2e-ZrmSU1hsJSKaA8vh0H3tg)
αν κάποιος θυμάται και στο περίπου τι ασκήσεις πέσαν ας πει! :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: soso on June 25, 2013, 11:09:32 am
έχει στο ισόγειο της πτέρυγας τις λύσεις. Οπότε στο περίπου καταλαβαίνει κανείς τι ζητάει... Το θέμα είναι να καταλάβουμε ακριβώς
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nvog1993 on August 08, 2013, 17:09:46 pm
Έχει κανείς τα θέματα λογισμού 2 του 13 να τα ανεβασει?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Fcoriolis on August 08, 2013, 17:25:32 pm
Θα τα είχαν στα downloads. Έχει ανέβει μόνο η δεύτερη πρόοδος του Ατρέα.
Έχει κανείς τα θέματα λογισμού 2 του 13 να τα ανεβασει?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: 4emonas on August 20, 2013, 14:28:37 pm
λογισμο 2 για το σεπτεμβριο απο που να διαβασω?? (ειμαι στο τμημα του ξενου και δεν εχω το βιβλιο του)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Elade on August 20, 2013, 14:42:52 pm
λογισμο 2 για το σεπτεμβριο απο που να διαβασω?? (ειμαι στο τμημα του ξενου και δεν εχω το βιβλιο του)
έχουν ανέβει φετινές σημειώσεις που νομίζω σε καλύπτουνTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: boudou on August 20, 2013, 14:57:32 pm
λογισμο 2 για το σεπτεμβριο απο που να διαβασω?? (ειμαι στο τμημα του ξενου και δεν εχω το βιβλιο του)
έχουν ανέβει φετινές σημειώσεις που νομίζω σε καλύπτουνρε μεγάλε, σίγουρα σε καλύπτουν; γιατί νομίζω ότι για την ύλη μετά την πρώτη πρόοδο υπάρχουν κάποιες ελλείψεις. επίσης, τα θέματα του ξένου τα έχει κανείς ή τουλάχιστον είναι ακόμα αναρτημένα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Elade on August 20, 2013, 15:20:42 pm
λογισμο 2 για το σεπτεμβριο απο που να διαβασω?? (ειμαι στο τμημα του ξενου και δεν εχω το βιβλιο του)
έχουν ανέβει φετινές σημειώσεις που νομίζω σε καλύπτουνρε μεγάλε, σίγουρα σε καλύπτουν; γιατί νομίζω ότι για την ύλη μετά την πρώτη πρόοδο υπάρχουν κάποιες ελλείψεις. επίσης, τα θέματα του ξένου τα έχει κανείς ή τουλάχιστον είναι ακόμα αναρτημένα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: theofilos on August 20, 2013, 17:37:11 pm
μπορει κανεις να ανεβασει ή να περιγραψει τα θεματα που εβαλε ο Ξενος στην εξεταστικη του Ιουνιου ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: 4emonas on August 26, 2013, 18:44:07 pm
μπορει κανεις να ανεβασει ή να περιγραψει τα θεματα που εβαλε ο Ξενος στην εξεταστικη του Ιουνιου ??
+1!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 02, 2013, 22:01:19 pm
Θεματα ιουνιου απο Ξενο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pepe on September 03, 2013, 13:01:57 pm
Μόλις ανέβασα τα θέματα Ιουνίου, τμήμα Ατρέα. Περιμένουν έγκριση από mod. Ξέρει κανείς αν είχε αναρτήσει ο Ατρέας και τα αποτελέσματα, όπως έκανε στις προόδους και στα Εφαρμοσμένα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 04, 2013, 18:08:12 pm
Θεματα ιουνιου απο Ξενο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 04, 2013, 18:11:45 pm
Μπορώ να σας περιγράψω τι έβαλε αλλά όχι ακριβώς.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 04, 2013, 18:20:33 pm
ε κανε ενα κοπο...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 04, 2013, 18:25:36 pm
Θεμα Α
Δίνει μια βαθμωτη συνάρτηση και ζητάει να βρούμε εφαπτομενο επιπεδο κάθετη ευθεία, μεγιστο και ελάχιστο ρυθμο μεταβολής προς συγκεκριμένη κατεύθυνση, το μέγιστο και ελάχιστο της συνάρτησης.
Θεμα Β
Δίνει ένα διανυσματικό πεδίο και ζητά να δείξουμε ότι είναι αστρόβιλο, να βρούμε βαθμωτο δυναμικό γενικά και σε ενα συγκεκριμένο σημείο, ισοσταθμική επιφάνεια για το βαθμωτο δυναμικό.
Θεμα Γ
Δίνει μια παραβολή και θέλει εμβαδόν και μήκος τόξου καμπύλης
Θεμα Δ
(α) Να βρουμε εμβαδον επιφάνειας κυλινδρου που κοβεται απο επίπεδο.
(β) Εφαρμογή θεωρηματος Gauss
Δίνει μια βαθμωτη συνάρτηση και ζητάει να βρούμε εφαπτομενο επιπεδο κάθετη ευθεία, μεγιστο και ελάχιστο ρυθμο μεταβολής προς συγκεκριμένη κατεύθυνση, το μέγιστο και ελάχιστο της συνάρτησης.
Θεμα Β
Δίνει ένα διανυσματικό πεδίο και ζητά να δείξουμε ότι είναι αστρόβιλο, να βρούμε βαθμωτο δυναμικό γενικά και σε ενα συγκεκριμένο σημείο, ισοσταθμική επιφάνεια για το βαθμωτο δυναμικό.
Θεμα Γ
Δίνει μια παραβολή και θέλει εμβαδόν και μήκος τόξου καμπύλης
Θεμα Δ
(α) Να βρουμε εμβαδον επιφάνειας κυλινδρου που κοβεται απο επίπεδο.
(β) Εφαρμογή θεωρηματος Gauss
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: haas on September 10, 2013, 18:37:00 pm
αν εχει κανεις τις λυσεις απο Ιουνιο 2013 του Ατρεα ας τις ανεβασει να ξεστραβωθουμε και εμεις λιγο...θενξ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Mumm-ra ο παντοντινός on September 11, 2013, 02:54:53 am
Θέματα Ιουνίου 2013 (Ξένος) στα downloads. Μια προσφορά της Νεολαίας Κονγκολέζων Ηλ-Μηχ ΑΠΘ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: morax on September 12, 2013, 00:58:03 am
παιζει κανεις π τα ξερει να γραψει ενδεικτικες λυσεις?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 12, 2013, 13:39:49 pm
ξερει κανεις πως υπολογιζουμε το μηκος της καμπυλης στο 3ο θεμα του ξενου ιουνιος '13? θα ανεβασω αργοτερα οσα ελυσα απο τον ιουνιο '13 αλλα δεν εγγυωμαι για αριθμητικα λαθη...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konsgkek on September 12, 2013, 18:47:51 pm
Όσοι έχουν κάποια ψυχανεμίσματα για το τι θα πέσει η κάποιο hint για το τι μπορεί να θεωρηθεί sos ή όχι, ας κάνει λίγο την καρδιά του ελαφρόπετρα και ας τα πει, ευχαριστά πολλά ^beg^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Chester on September 13, 2013, 13:05:16 pm
ξερει κανεις πως υπολογιζουμε το μηκος της καμπυλης στο 3ο θεμα του ξενου ιουνιος '13? θα ανεβασω αργοτερα οσα ελυσα απο τον ιουνιο '13 αλλα δεν εγγυωμαι για αριθμητικα λαθη...
Οταν μπορεσεις ανεβασε αυτα που ελυσες :-\
Το μήκος μήπως υπολογιζεται ως το ολοκλήρωμα του μέτρου της παραγώγου της συνάρτησης που περγράφει το χωρίο; :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geralt on September 13, 2013, 13:18:40 pm
Μπορει να πει καποιος πως λυνεται το θεμα 1β του Ατρεα? Ιουνιος 2013
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Κηπουρίδης on September 13, 2013, 13:48:02 pm
Μπορει να πει καποιος πως λυνεται το θεμα 1β του Ατρεα? Ιουνιος 2013
Μη σε πάρω και στο λαιμό μου, νομίζω ότι :
Ξέρουμε ότι z=F(u,v), άρα dF = Fu*du + Fv*dv (1)
Θέτουμε u = x-y => du = dx-dy και v = x+y => dv = dx+dy (2)
Ξέρουμε επίσης ότι F(x-y,x+y)=0, άρα F(u,v)=0, άρα dF = 0, κι εδώ αντικαθιστούμε την (1), άρα έχουμε
Fu*du + Fv*dv = 0
αντικαθιστούμε τα du και dv οπότε :
Fu*(dx-dy)+Fv*(dx+dy) = 0 => (Fu+Fv)*dx + (Fv-Fu)*dy = 0 => dy/dx = -(Fu+Fv)/(Fv-Fu)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: FireStarter on September 13, 2013, 18:30:12 pm
Μια ιδεα που εχω για το μηκος της καμπυλης ειναι η εξης:
L=Επικαμπυλιο (dr) = ολοκήρωμα [α->β] (1*|r'(t)|dt)
Παραμετροποιουμε την καμπυλη ως εξης:
1. Ευθυγραμμο τμημα απο τα σημεια (3,-2) εως (0,1), r1(t)=(3-3t, -2+3t) 0<t<1
2. Θετικό τμημα παραβολης r2(t)=(t, sqrt(t+1)) -1>t>0
3. Αρνητικο τμημα παραβολης r3(t)=(t, -sqrt(t+1)) -1<t<3
L=L1+L2+L3
Το L1 βγαινει ευκολα. Στα αλλα 2 ζοριζομαι.
Ιδεες;
L=Επικαμπυλιο (dr) = ολοκήρωμα [α->β] (1*|r'(t)|dt)
Παραμετροποιουμε την καμπυλη ως εξης:
1. Ευθυγραμμο τμημα απο τα σημεια (3,-2) εως (0,1), r1(t)=(3-3t, -2+3t) 0<t<1
2. Θετικό τμημα παραβολης r2(t)=(t, sqrt(t+1)) -1>t>0
3. Αρνητικο τμημα παραβολης r3(t)=(t, -sqrt(t+1)) -1<t<3
L=L1+L2+L3
Το L1 βγαινει ευκολα. Στα αλλα 2 ζοριζομαι.
Ιδεες;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: 4emonas on September 13, 2013, 21:42:37 pm
υπαρχει κανεις που να γνωριζει σιγουρα εαν θα επιρεαστει το μαθημα απο απεργιες???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: babyflo on September 13, 2013, 22:11:53 pm
Μια ιδεα που εχω για το μηκος της καμπυλης ειναι η εξης:
L=Επικαμπυλιο (dr) = ολοκήρωμα [α->β] (1*|r'(t)|dt)
Παραμετροποιουμε την καμπυλη ως εξης:
1. Ευθυγραμμο τμημα απο τα σημεια (3,-2) εως (0,1), r1(t)=(3-3t, -2+3t) 0<t<1
2. Θετικό τμημα παραβολης r2(t)=(t, sqrt(t+1)) -1>t>0
3. Αρνητικο τμημα παραβολης r3(t)=(t, -sqrt(t+1)) -1<t<3
L=L1+L2+L3
Το L1 βγαινει ευκολα. Στα αλλα 2 ζοριζομαι.
Ιδεες;
L=Επικαμπυλιο (dr) = ολοκήρωμα [α->β] (1*|r'(t)|dt)
Παραμετροποιουμε την καμπυλη ως εξης:
1. Ευθυγραμμο τμημα απο τα σημεια (3,-2) εως (0,1), r1(t)=(3-3t, -2+3t) 0<t<1
2. Θετικό τμημα παραβολης r2(t)=(t, sqrt(t+1)) -1>t>0
3. Αρνητικο τμημα παραβολης r3(t)=(t, -sqrt(t+1)) -1<t<3
L=L1+L2+L3
Το L1 βγαινει ευκολα. Στα αλλα 2 ζοριζομαι.
Ιδεες;
Παραβολή θέτεις y=t και ευθεία θέτεις x=t.Και έχεις δύο ολκληρώματα.Της παραβολής βγαίνει sqrt(4t^2+1) νομίζω το οποίο είναι έκτρωμα αλλά έτσι είναι.Στον λογισμό 1 αν θες δες πως υπολογίζεται.Δεν πιστεύω πάντως να μην έδινε όλες τις μονάδες αν το άφηνες εκεί.Το πολύ να έκοβε 0,2 το οποίο αν το χρειαζόσουν για να περάσεις θα το έπαιρνες.Αυτά.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 14, 2013, 12:34:46 pm
Όσοι έχουν κάποια ψυχανεμίσματα για το τι θα πέσει η κάποιο hint για το τι μπορεί να θεωρηθεί sos ή όχι, ας κάνει λίγο την καρδιά του ελαφρόπετρα και ας τα πει, ευχαριστά πολλά ^beg^
για τον ξενο τουλαχιστον από οτι εχω δει και στους πολιτικους μηχανικους τα θεματα του επαναλαμβανονται...δηλαδη τα 2 πρωτα θεματα του ιουνιου ειναι στανταρ και στανταρ να υπολογιστει ενα εμβαδο και συνηθως και το θεωρημα green.
Ιουνιος 2013 ξενος
θεμα 1ο
α) |u|=sqrt(42+02+32)
u=(4,0,3) uo=(4/|u|, 0/|u|, 3/|u|)
gradf= fxi +fyj +fzk |P
Du= graf * uo
max: Du= | gradf | |a| cosφ για max Du εχουμε cosφ=1 => a= gradf/ |gradf| και μεγιστη τιμη |gradf|
min: αντιστοιχα για min cosφ= -1 a=- (gradf/|gradf|)
β) απο το θεωρημα για τα ακροτατα τριων μεταβλητων βρηκα ενα min στο f(4,1,0)= -32
γ) ισοσσταθμικη : f(x,y,z) = x^3-6x^2+y^2+z^2-2y+1=c
για το σημειο Α(1,0,1) βρισκω c= -3
εφαπτομενο επιπεδο στο σημειο Μ(2,2,2sqrt3) Fx(x-x0)+Fy(y-yo)+Fz(z-z0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Chester on September 14, 2013, 13:28:24 pm
για τον ξενο τουλαχιστον από οτι εχω δει και στους πολιτικους μηχανικους τα θεματα του επαναλαμβανονται...δηλαδη τα 2 πρωτα θεματα του ιουνιου ειναι στανταρ και στανταρ να υπολογιστει ενα εμβαδο και συνηθως και το θεωρημα green.
Αν είναι έτσι αν μπορείς γράψε και τα υπόλοιπα αν τα έλυσες. Είσαι ωραίος πάντως ;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: haas on September 14, 2013, 14:56:25 pm
Ατρεας Ιουνιος 2013
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: niko on September 14, 2013, 18:00:22 pm
r(t)=(x,y,z) προσθετεις κατα μελη και εχεις x=1,y=2z-1 αρα r(t)=(1,2t-1,t) με t απο -1 μεχρι 2 (ετσι νομιζω τουλαχιστον)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mixanikos on September 14, 2013, 23:18:25 pm
παιδια μηπως μπορει καποιος να δωσει καποια βοηθεια σχετικα με το 4ο θεμα Ιουνιου του Ξενου? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnis32 on September 15, 2013, 01:31:27 am
Ένα καλό βιβλίο είναι το Calculus του Larson. Άμα πας στην σελίδα 1110 θα βρείς την απάντηση.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aussie on September 15, 2013, 02:05:53 am
Ένα καλό βιβλίο είναι το Calculus του Larson. Άμα πας στην σελίδα 1110 θα βρείς την απάντηση.
για τι εκδοση μιλαμε?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sok on September 15, 2013, 03:16:52 am
Παιδιά μια παράκληση και εγώ όποιος έχει λυμένα τα θέματα του Ξένου ας κάνει ένα κόπο να τα ανεβάσει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnis32 on September 15, 2013, 13:24:30 pm
10η έκδοση. Όσο για το δεύτερο υποερώτημα νομίζω παίρνεις το επικαμπύλιο ολοκλήρωμα της επίφάνειας 2χ+4υ+ζ=16 με καμπύλη ολοκλήρωσης την χ^2+υ^2=4 αφού την κάνεις παραμετρική, χωρίς να είμαι σίγουρος.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnis32 on September 15, 2013, 13:42:17 pm
Βασικά λάθος. Έτσι υπολογίζεις της εξωτερικής επιφάνειας του κυλίνδρου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: johnis32 on September 15, 2013, 13:45:33 pm
Μάλλον λύνετε όπως στην σελίδα 1004
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Chester on September 15, 2013, 13:50:56 pm
Έτσι λύνεται. Ήταν η προτελευταία άσκηση που έκανε ο Ξένος στην αίθουσα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: morax on September 15, 2013, 17:45:02 pm
απο θεματα ξενου τα ολοκληρωματα ποσο βγαινουν? γενικα εχει κανεις λυσεις απο ξενο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: FireStarter on September 15, 2013, 18:35:27 pm
Ατρεας Ιουνιος 2013
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Είχα κολλήσει κι εγώ εδώ. Στα downloads υπάρχουν οι σημειώσεις από τα μαθήματα του Ατρέα. Αν τις κατεβάσεις, στις σελίδες 120-121 του pdf θα δείς πως το κάνει.
Έπειτα το έλυσα όπως την άσκηση 4 από τις λυμένες του κεφαλαίου 7.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: haas on September 15, 2013, 19:31:17 pm
Ατρεας Ιουνιος 2013
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Είχα κολλήσει κι εγώ εδώ. Στα downloads υπάρχουν οι σημειώσεις από τα μαθήματα του Ατρέα. Αν τις κατεβάσεις, στις σελίδες 120-121 του pdf θα δείς πως το κάνει.
Έπειτα το έλυσα όπως την άσκηση 4 από τις λυμένες του κεφαλαίου 7.
thanx man.σωστο σε βρισκω.φανταζομαι βγαινει το ιδιο και με τους 2 τροπους :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 15, 2013, 19:41:29 pm
Δηλαδη ποια παραμετροποιηση πηρατε?
sorry το χει απο πισω
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Chester on September 15, 2013, 20:26:59 pm
Θέμα 3α Ξενου τι αποτέλεσμα βγάζετε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 20:49:59 pm
Θέμα 3α Ξενου τι αποτέλεσμα βγάζετε;
10/3 μου βγηκε....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Chester on September 15, 2013, 20:58:06 pm
πω.. Η αρχική μορφή του ολοκληρώματος σου μαζί με τα όρια ποια είναι;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 15, 2013, 21:00:48 pm
9/2 αλλα δεν εγγυωμαι συχνα μου ξεφευγουν πραματα στα ολοκληρωματα
εξωτερικο ολοκληρωμα απο -2 μεχρι 1 dy
εσωτερικο απο y2-1 μεχρι 1-y dx
κενο μεσα
υ.γ. σορρυ δε ξερω να γραφω ολοκληρωματα σε ποστ
εξωτερικο ολοκληρωμα απο -2 μεχρι 1 dy
εσωτερικο απο y2-1 μεχρι 1-y dx
κενο μεσα
υ.γ. σορρυ δε ξερω να γραφω ολοκληρωματα σε ποστ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 21:26:28 pm
9/2 αλλα δεν εγγυωμαι συχνα μου ξεφευγουν πραματα στα ολοκληρωματα
εξωτερικο ολοκληρωμα απο -2 μεχρι 1 dy
εσωτερικο απο y2-1 μεχρι 1-y dx
κενο μεσα
υ.γ. σορρυ δε ξερω να γραφω ολοκληρωματα σε ποστ
εξωτερικο ολοκληρωμα απο -2 μεχρι 1 dy
εσωτερικο απο y2-1 μεχρι 1-y dx
κενο μεσα
υ.γ. σορρυ δε ξερω να γραφω ολοκληρωματα σε ποστ
σωστα ρε φιλε αλλα γιατι απο -2 και οχι απο -1???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aredhel on September 15, 2013, 21:28:09 pm
Στο 3α του Ξένου και εγώ 10/3 έχω αποτέλεσμα.Αν έχει λύσει κάποιος το 4 ας πει αποτελέσματα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Μικρή Ηλιαχτίδα on September 15, 2013, 21:28:48 pm
Αν είστε παλιοί για το θέμα 3α του ξένου είναι στο πορτοκαλί βιβλίο σελίδα 376 παράδειγμα 4.5. Είναι ακριβώς η ίδια άσκηση για το εμβαδόν. Για το 3β καμιά ιδέα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 15, 2013, 21:31:58 pm
σωστα ρε φιλε αλλα γιατι απο -2 και οχι απο -1???
γιατι τα σημεια τομης των δυο καμπυλων ειναι το (0,1) και το (3,-2) φτιαξε ενα σχημα θα σε βοηθησει
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 21:38:52 pm
4ο θεμα ξενος
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 21:40:30 pm
σωστα ρε φιλε αλλα γιατι απο -2 και οχι απο -1???
γιατι τα σημεια τομης των δυο καμπυλων ειναι το (0,1) και το (3,-2) φτιαξε ενα σχημα θα σε βοηθησει
έχεις δικιο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: aredhel on September 15, 2013, 21:44:46 pm
4ο θεμα ξενος
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
Βασικά εάν μπορείς να πεις λίγο αναλυτικά πως την έλυσες.Δεν μπορώ να την βγάλω.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 21:59:12 pm
4ο θεμα ξενος
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: morax on September 15, 2013, 22:11:36 pm
2β και γ ετσι να μ πει καποιος πως γινονται αν μπορει θενκς
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 22:13:02 pm
καποιος τα θέματα της 2ης προοδου απο τον ξένο έστω και στο περίπου ???//
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 22:18:56 pm
2β και γ ετσι να μ πει καποιος πως γινονται αν μπορει θενκς
έχεις F(x,y,z)= (p,g,r)
για να βρεις το δυναμικο V ολοκληρωνεις ως προς χ το p ως προς y το g και ως προς z το r τα προσθέτεις και ολα αυτα θα σου βγάλουν μια σταθερά γιατί ειναι αόριστα ολοκληρωματα οπότε βρίσκεις την c απο το σημείο που σου δίνει
για το έργο απλά αφαιρείς το V(B)-V(A) διότι έχει συντηριτικό πεδίο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 15, 2013, 22:21:12 pm
εγω τα ελυσα ως εξης:
2β) V= (ολοκληρωμα απο 0-χ)P(x,y,z) dx + (ολοκληρωμα απο 0-y) Q(0,y,z) dy + (ολοκληρωμα απο 0-z) R(0,0,z) dz
V=(λυση του ολοκληρωματος)+c
για V(1,2,-1)=12 και βρισκω c= -19 edit:ενας μωρε δε το ειδε να το διορθωσει? c= -1
2γ) εφαρμοζεις ενα θεωρημα για συντηρητικα πεδια που ειναι στο μπλε, παλιο βιβλιο σελ. 338 V(B)-V(A)= εργο
2β) V= (ολοκληρωμα απο 0-χ)P(x,y,z) dx + (ολοκληρωμα απο 0-y) Q(0,y,z) dy + (ολοκληρωμα απο 0-z) R(0,0,z) dz
V=(λυση του ολοκληρωματος)+c
για V(1,2,-1)=12 και βρισκω
2γ) εφαρμοζεις ενα θεωρημα για συντηρητικα πεδια που ειναι στο μπλε, παλιο βιβλιο σελ. 338 V(B)-V(A)= εργο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Μικρή Ηλιαχτίδα on September 15, 2013, 22:37:28 pm
Στο 2α του ξένου μας είχε επισημάνει ο Ξένος οτι δεν πρέπει να δείξουμε ότι είναι αστρόβιλο αλλά ότι είναι συντηρητικό. Έπρεπε απλά να αποδείξουμε πως είναι αστρόβιλο και επειδή ο τόπος είναι απλά συνεκτικός άρα είναι και συντηρητικό?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 15, 2013, 22:40:57 pm
4ο θεμα ξενος
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
στο α) εγώ βρήκα μόνο το 128π. Το ολοκλήρωμα απτο ημίτοτο και συνημήτονο έβγαινε 0...βέβαια μπορεί να έκανα κάποιο λάθος εδώ.
στο β) έβγαλα 4π* (ρίζα)21
μάλλον ξέχασες να βάλεις στο ολοκλήρωμα μέσα το μέτρο( Rx X Ry)
όπου R = (x, y, 2x+4y-16)
σαν το β είχε κάνει μια ολόιδια άσκηση στο μάθημα
---------------
Το 3β πώς λύνεται??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 15, 2013, 22:43:01 pm
Στο 2α του ξένου μας είχε επισημάνει ο Ξένος οτι δεν πρέπει να δείξουμε ότι είναι αστρόβιλο αλλά ότι είναι συντηρητικό. Έπρεπε απλά να αποδείξουμε πως είναι αστρόβιλο και επειδή ο τόπος είναι απλά συνεκτικός άρα είναι και συντηρητικό?
απο τις σχεσεις που ισχυουν για τα grad, div, rot επειδη αν το F ειναι συντηρητικο υπαρχει βαθμωτο πεδιο f τετοιο ωστε F=gradf
και rot (gradf)= rotF=0 γι αυτο αρκει να αποδειξεις οτι ειναι αστροβιλο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 22:43:29 pm
Στο 2α του ξένου μας είχε επισημάνει ο Ξένος οτι δεν πρέπει να δείξουμε ότι είναι αστρόβιλο αλλά ότι είναι συντηρητικό. Έπρεπε απλά να αποδείξουμε πως είναι αστρόβιλο και επειδή ο τόπος είναι απλά συνεκτικός άρα είναι και συντηρητικό?
ναιTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: rackella on September 15, 2013, 22:59:54 pm
μήπως πρεπει το ολοκλήρωμα στο 2β να ειναι απο 1 ως χ απο 2 ως ψ και απο -1 ως ζ?
γτ στο μπλε βιβλιο στη σελιδα 147 εχει ενα τυπο αλλα λεει πως αν δ διευκρινιζεται κατι αλλο τα βαζουμε ισα με 0.
γτ στο μπλε βιβλιο στη σελιδα 147 εχει ενα τυπο αλλα λεει πως αν δ διευκρινιζεται κατι αλλο τα βαζουμε ισα με 0.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 23:04:11 pm
4ο θεμα ξενος
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
στο α) εγώ βρήκα μόνο το 128π. Το ολοκλήρωμα απτο ημίτοτο και συνημήτονο έβγαινε 0...βέβαια μπορεί να έκανα κάποιο λάθος εδώ.
στο β) έβγαλα 4π* (ρίζα)21
μάλλον ξέχασες να βάλεις στο ολοκλήρωμα μέσα το μέτρο( Rx X Ry)
όπου R = (x, y, 2x+4y-16)
σαν το β είχε κάνει μια ολόιδια άσκηση στο μάθημα
---------------
Το 3β πώς λύνεται??
έχεις δικιο για το α
στο β όμως απλά το ολοκλήρωμα είναι το εμβαδον του κύκλου αφού είμαστε στο Oχy (προβολή κυλίνδρου) διότι το z=0 ε??? το ριζα 21 απε που ????
αν μπορείς εξηγα το λίγο γιατί έχεις ένα point
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 15, 2013, 23:15:04 pm
4ο θεμα ξενος
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
α)16 +128*π
β) 4π (εφοσον το z=0 παίρνω τις προβολες στον Οχy του κυλινδρου και του άλλου σχηματος που είναι ένα τρισδιάστατο τρίγωνο )
στο α) εγώ βρήκα μόνο το 128π. Το ολοκλήρωμα απτο ημίτοτο και συνημήτονο έβγαινε 0...βέβαια μπορεί να έκανα κάποιο λάθος εδώ.
στο β) έβγαλα 4π* (ρίζα)21
μάλλον ξέχασες να βάλεις στο ολοκλήρωμα μέσα το μέτρο( Rx X Ry)
όπου R = (x, y, 2x+4y-16)
σαν το β είχε κάνει μια ολόιδια άσκηση στο μάθημα
---------------
Το 3β πώς λύνεται??
έχεις δικιο για το α
στο β όμως απλά το ολοκλήρωμα είναι το εμβαδον του κύκλου αφού είμαστε στο Oχy (προβολή κυλίνδρου) διότι το z=0 ε??? το ριζα 21 απε που ????
αν μπορείς εξηγα το λίγο γιατί έχεις ένα point
Ισχύει ο τύπος στα επιφανειακά ολοκληρώματα (ολοκλήρωμα στο D) [ (μέτρο) Rx X Ry ] dxdy
όπου το R είναι όπως το έγραψα πριν...
το (μέτρο) Rx X Ry βγαίνει ρίζα21.
αντικαθιστάς...πολικές συντεταγμένες...κτλ κτλ...από κει και πέρα είναι όπως το έκανες κι εσύ
είναι ο κλασικός τρόπος για τα επιφανειακά 1ου τύπου
για το 3β κανείς?.. :-\ γιατί δεν θυμάμαι να διάβασα πουθενά πώς υπολογίζουμε το μήκος συνόρου μιας καμπύλης...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 23:19:29 pm
δεν είναι ακριβώς ίδια με αυτήν που έχει στις σημειώσεις του διότι δεν σου λέει το επίπεδο z=0 σου έχει μονο τον κίλυνδρο και το επίπεδο με z
το ότι μας μηδενίζει το z μας παει σε ολοκλρηρώματα διπλά και όχι σε επιφανειακά που πρέπει να εκφράσεις το ds
ε?????????
το ότι μας μηδενίζει το z μας παει σε ολοκλρηρώματα διπλά και όχι σε επιφανειακά που πρέπει να εκφράσεις το ds
ε?????????
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 15, 2013, 23:24:39 pm
δεν είναι ακριβώς ίδια με αυτήν που έχει στις σημειώσεις του διότι δεν σου λέει το επίπεδο z=0 σου έχει μονο τον κίλυνδρο και το επίπεδο με z
το ότι μας μηδενίζει το z μας παει σε ολοκλρηρώματα διπλά και όχι σε επιφανειακά που πρέπει να εκφράσεις το ds
ε?????????
το ότι μας μηδενίζει το z μας παει σε ολοκλρηρώματα διπλά και όχι σε επιφανειακά που πρέπει να εκφράσεις το ds
ε?????????
εγώ νομίζω ότι είναι όπως με αυτήν στις σημειώσεις...(άμα εννοούμε την ίδια...χαχα). δλδ ότι λύνεται με επιφανειακό ολοκλήρωμα...
δε νομίζω ότι επηρεάζει εδώ το z...Την κυρτή επιφάνεια υπολογίζεις. Εκτός άμα το έχω καταλάβει λάθος :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 23:41:10 pm
παιζει να έχει πάλι δικιο!!!!!!
οσο για το 3β μια αποψη
το στοιχειωδης μήκος γενικά έιναι ds= ριζα(1 +(dy/dx)^2) άρα ολοκλήρώνεις αυτό ως προς χ αλλά βγαίνει ένα δύσκολο ολοκλήρωμα που πρέπει να έχεις τυπολογίο για να το βγάλεις οπότε δεν νομίζω να είχε βάλει κάτι τετόιο αλλα δεν ξέρω κιόλας
πείτε και κανα άλλος καμιά άποψη
οσο για το 3β μια αποψη
το στοιχειωδης μήκος γενικά έιναι ds= ριζα(1 +(dy/dx)^2) άρα ολοκλήρώνεις αυτό ως προς χ αλλά βγαίνει ένα δύσκολο ολοκλήρωμα που πρέπει να έχεις τυπολογίο για να το βγάλεις οπότε δεν νομίζω να είχε βάλει κάτι τετόιο αλλα δεν ξέρω κιόλας
πείτε και κανα άλλος καμιά άποψη
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pezouna on September 15, 2013, 23:44:31 pm
4ο θεμα ξενος
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
η απλά κάνεις Gauss κ κοιτάς και το παράδειγμα σελ 506 στο μπλε και βγαίνει 128π. δεν νομίζω να παρέλειψα κάτι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: status_quo on September 15, 2013, 23:45:40 pm
εγω να ρωτησω κατι τελειως οφφ τοπικ?
μηπως ξερουμε πως καθομαστε στις αιθουσες?γιατι στην προοδο θυμαμαι μας βαζαν ανα στηλη ατρεασ/ξενος
μηπως ξερουμε πως καθομαστε στις αιθουσες?γιατι στην προοδο θυμαμαι μας βαζαν ανα στηλη ατρεασ/ξενος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on September 15, 2013, 23:56:25 pm
4ο θεμα ξενος
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
α ερωτημα
p=διπλο ολοκληρωμα( G*n0*ds)
G(y,x,2*(16-2x-4x) κανεις αντικατασταση το z απο την συναρτηση που σου δίνει με z
μετά θεωρεις φ(x,y,z)=z-16+2x+4y
βρίσκεις το μοναδιαίο n0=gradφ/μετρο(gradφ)=(2,4,1)/riza21
το ds=ριζα{(θz/θχ)^2 +(θz/θy)^2+1}dxdy=riza21dxdy
βαλτα ολα μεσα στο ολοκληρωμα και μετα για τα ορια του ολοκληρωματος( κανε πολικες) οποτε εχεις ορια απο 0 εως 2π και απο 0εως 2 (χ^2+y^2=4)
η απλά κάνεις Gauss κ κοιτάς και το παράδειγμα σελ 506 στο μπλε
τι αποτέλεσμα έβγαλες???τόσο απλά
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sok on September 16, 2013, 03:30:51 am
Βρήκε κανείς πως λύνεται το 3β) του Ξένου;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: rackella on February 10, 2014, 02:30:57 am
έχει λύσει κανείς τα θέματα του Σεπτέμβρη απο Ξένο;
αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on February 10, 2014, 02:35:23 am
έχει λύσει κανείς τα θέματα του Σεπτέμβρη απο Ξένο;
αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
Aν ασχοληθουμε λιγο με παλια θεματα λες να βγαινει το μαθημα μεχρι την τριτη ? (εστω να το περασουμε μονο)αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: rackella on February 10, 2014, 14:37:02 pm
έχει λύσει κανείς τα θέματα του Σεπτέμβρη απο Ξένο;
αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
Aν ασχοληθουμε λιγο με παλια θεματα λες να βγαινει το μαθημα μεχρι την τριτη ? (εστω να το περασουμε μονο)αν ναι ας κανει ενα κοπο να ατ ανεβασει...πλιζ. :(
τριτη ειναι αυριο..ειναι θεμα τυχης αυτο.αμα πεσουν ιδια..μπορει και να περασεις..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on February 10, 2014, 18:38:35 pm
Aπο τα θεματα του ατρεα Ιουνιος 13 ομαδα β.
Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Neal on February 10, 2014, 18:57:01 pm
Το χει απαντήσει κάποιος μερικές σελίδες πριν.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on February 10, 2014, 20:36:35 pm
Aπο τα θεματα του ατρεα Ιουνιος 13 ομαδα β.
Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Στο ιδιο θεμα το Γ πως λυνεται ??Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: afroditeschild on February 10, 2014, 20:53:12 pm
τέταρτο θέμα το β ιούνιος 2013 ξένος κάποιος..... κάποια άποψη????
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Neal on February 10, 2014, 22:07:38 pm
Aπο τα θεματα του ατρεα Ιουνιος 13 ομαδα β.
Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Στο ιδιο θεμα το Γ πως λυνεται ??Η ασκηση 3 το Β πως λυνεται απλη παραμετροποιηση ειναι ? (γιατι με μπερδευει που εχει την καμπυλη σαν 2 ευθειες)
Είναι στην ουσία θεώρημα Green. Το ολοκλήρωμα F*e0*ds (έργο) = ολοκλήρωμα F*dr και εφαρμόζεις θεώρημα Green. θQ/θx - θP/θy = 1 + 2 = 3 => διπλό ολοκλήρωμα 3dxdy = 3 * εμβαδόν χωρίου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on February 11, 2014, 14:20:06 pm
Τα σημερινα θεματα ομαδα Α
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kostasnafs on June 03, 2014, 14:48:18 pm
στα θεματα του σεμπτεμβριου του 2013,στο θεμα 2α) τι ακριβως πρεπει να κανουμε? Συγκεκριμενα λεει: "Δινεται η εξισωση: F(x,y,z)= z^3 + xz - y^3 - 1=0. Να αποδειξετε οτι η παραπανω εξισωση οριζει σε πεπλεγμενη μορφη συναρτηση z=z(x,y) σε μια περιοχη του σημειου (1,1) με z(1,1)=1 "
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: NaVi.Mitsos on June 13, 2014, 14:06:07 pm
στα θεματα του σεμπτεμβριου του 2013,στο θεμα 2α) τι ακριβως πρεπει να κανουμε? Συγκεκριμενα λεει: "Δινεται η εξισωση: F(x,y,z)= z^3 + xz - y^3 - 1=0. Να αποδειξετε οτι η παραπανω εξισωση οριζει σε πεπλεγμενη μορφη συναρτηση z=z(x,y) σε μια περιοχη του σημειου (1,1) με z(1,1)=1 "
έχει 2 τρόπους λύσεις.θα σου πώ αυτόν π δεν χρειάζεται να χρησιμοποιήσεις τύπο.παραγωγίζεις την f ως προς χ η ως προς y θεωρωντας z=z(x,y) λυνεις ως προς z' και αν σου βγει στον παρονομαστη 0 αφου πρωτα αντικαταστησεις τις συντεταγμενες τοτε δεν οριζεται πεπλεγμενη μορφη...
Εχω και εγω μια απορια οταν λεμε βρες τη ροη του δ.π ως προς την θετικη οψη στην ουσια στο ολοκληρωμα θα εχει + απο μπροστα ενω στην αντιθετη περιπτωση μιον;
Κ οταν λεμε βρες την ροη του δ.π ως προς την πανω οψη τι κανουμε; ευχαριστω εκ των προτερων
Επίσης μια βοηθεια για το θεμα 4 του ιουνίου του 2013
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Marmotakos on June 13, 2014, 18:30:34 pm
κανένα hint στο θέμα 4 σεπτεμβρίου του 13 με την σφαίρα και τη θερμοκρασία?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kourdisto_portokali on June 14, 2014, 00:51:01 am
κανένα hint στο θέμα 4 σεπτεμβρίου του 13 με την σφαίρα και τη θερμοκρασία?
κ εγω κολλησα σ αυτη...προσπαθησα να τη λυσω οπως μια παρομοια στις σημειωσεις του ατρεα ( ασκ 9 κεφ. 3 απο τις λυμενες ) ...βρηκα τα ακροτατα πανω στο συνορο της σφαιρας ( αν ξερεις καποιος ας εξηγησει πως διακρινω αν ειναι ελαχιστα η μεγιστα) αλλα οταν παω να βρω τα ακροτατα στο εσωτερικο κ μηδενιζω τις μερικες παραγωγους της συναρτησης καταληγω σε ατοπο αφου αυτες ειναι σταθερες :???: ξερεις κανεις τι παιζει;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 02:02:04 am
Βασικά δύο είναι νομίζω οι πιθανές απαντήσεις.
1) δεν υπάρχει στο εσωτερικό μεγιστη και ελάχιστη(γιατι ουσιαστικη συμπίπτει με την μεγιστη ελάχιστη πάνω στην σφαίρα .....(μαλλον λίγο αόριστη γιατι γενικά αυξάνει προς μια συγκεκριμένη κατεύθυνση που δίνεται απο το διανυσμα (1,-2,2))
2) Ρωτάει στην αρχή ποια είναι τα σημεία της σφαίρας (Εσωτερικου και συνόρου και βρίσκουμε με την μεθοδο Lagrange πάνω στην σφαίρα) και σαν δευτερη ερώτηση τις τιμες της μέγιστης/ελάχιστης θερμοκρασίας που μάλλον αυτό πιστεύω είναι το σωστο.
1) δεν υπάρχει στο εσωτερικό μεγιστη και ελάχιστη(γιατι ουσιαστικη συμπίπτει με την μεγιστη ελάχιστη πάνω στην σφαίρα .....(μαλλον λίγο αόριστη γιατι γενικά αυξάνει προς μια συγκεκριμένη κατεύθυνση που δίνεται απο το διανυσμα (1,-2,2))
2) Ρωτάει στην αρχή ποια είναι τα σημεία της σφαίρας (Εσωτερικου και συνόρου και βρίσκουμε με την μεθοδο Lagrange πάνω στην σφαίρα) και σαν δευτερη ερώτηση τις τιμες της μέγιστης/ελάχιστης θερμοκρασίας που μάλλον αυτό πιστεύω είναι το σωστο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kourdisto_portokali on June 14, 2014, 02:33:07 am
Βασικά δύο είναι νομίζω οι πιθανές απαντήσεις.
1) δεν υπάρχει στο εσωτερικό μεγιστη και ελάχιστη(γιατι ουσιαστικη συμπίπτει με την μεγιστη ελάχιστη πάνω στην σφαίρα .....(μαλλον λίγο αόριστη γιατι γενικά αυξάνει προς μια συγκεκριμένη κατεύθυνση που δίνεται απο το διανυσμα (1,-2,2))
2) Ρωτάει στην αρχή ποια είναι τα σημεία της σφαίρας (Εσωτερικου και συνόρου και βρίσκουμε με την μεθοδο Lagrange πάνω στην σφαίρα) και σαν δευτερη ερώτηση τις τιμες της μέγιστης/ελάχιστης θερμοκρασίας που μάλλον αυτό πιστεύω είναι το σωστο.
Θενκς ;) 1) δεν υπάρχει στο εσωτερικό μεγιστη και ελάχιστη(γιατι ουσιαστικη συμπίπτει με την μεγιστη ελάχιστη πάνω στην σφαίρα .....(μαλλον λίγο αόριστη γιατι γενικά αυξάνει προς μια συγκεκριμένη κατεύθυνση που δίνεται απο το διανυσμα (1,-2,2))
2) Ρωτάει στην αρχή ποια είναι τα σημεία της σφαίρας (Εσωτερικου και συνόρου και βρίσκουμε με την μεθοδο Lagrange πάνω στην σφαίρα) και σαν δευτερη ερώτηση τις τιμες της μέγιστης/ελάχιστης θερμοκρασίας που μάλλον αυτό πιστεύω είναι το σωστο.
Παντως θα βοηθουσε αρκετα οσοι λυνουν θεματα να τα ανεβαζουν :-[ :-[
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 02:42:34 am
το θεμα 8 Φεβρουαριος 14 λυνεται με κλασσικο ορισμο ροης η υπαρχει και ποιο ευκολος τροπος ? .
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 02:45:04 am
Με Gauss λύνεται.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 02:51:47 am
ξερεις ποια θα ειναι τα ορια του τριπλου ? και πως τα βρισκω ?
(η μηπως κατευθειαν πολικες ? )
(η μηπως κατευθειαν πολικες ? )
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 02:53:12 am
Σε λιγάκι θα ανεβάσω μια λύση ελπίζω σωστή:)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 02:54:08 am
θενκς φιλος !! (μπορει και φιλη δεν ξερω :P )
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: tsiantis on June 14, 2014, 12:32:15 pm
paidia mia erwtisi...
sto kefalaio 7 tis dianismatikis analisis(kampilogrammes syntetagmenes) exei enan tipo gia na ipologisei to embado epifaneis.
omws emeis exeoume mathei allo tropo ipologismou embadou tis epifaneias.... (dipla oloklirwmata, logismos pollwn metavlitwn, theorima green)
pote xrismopoioume ton enan tipo kai pote ton allo?
sto kefalaio 7 tis dianismatikis analisis(kampilogrammes syntetagmenes) exei enan tipo gia na ipologisei to embado epifaneis.
omws emeis exeoume mathei allo tropo ipologismou embadou tis epifaneias.... (dipla oloklirwmata, logismos pollwn metavlitwn, theorima green)
pote xrismopoioume ton enan tipo kai pote ton allo?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 12:43:03 pm
Όταν η επιφάνεια δεν ειναι επίπεδη( είναι δηλδή κυρτή ) όπως παράδειγμα ή επιφάνειας μιας σφαίρας ή η κυρτή ενός κυλίνδρου πρέπει να πάρεις αυτόν τον τύπο.
Με τα διπλά ολοκληρώματα όλες οι επιφάνειες ήταν επίπεδες (πάνω στο επίπεδο xOy)
Με τα διπλά ολοκληρώματα όλες οι επιφάνειες ήταν επίπεδες (πάνω στο επίπεδο xOy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cortex on June 14, 2014, 13:30:51 pm
σεπτέμβριος του 13 θέμα 2 το β ο taylor θα γίνει F(x,ψ,z)=F(1,1,1)+ 1/1! [dF/dx(1,1,1) (x-1) + dF/dψ(1,1,1) (ψ-1) + dF/dz(1,1,1) (z-1) ή κάνω κάποιο λάθος;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 13:36:19 pm
σεπτέμβριος του 13 θέμα 2 το β ο taylor θα γίνει F(x,ψ,z)=F(1,1,1)+ 1/1! [dF/dx(1,1,1) (x-1) + dF/dψ(1,1,1) (ψ-1) + dF/dz(1,1,1) (z-1) ή κάνω κάποιο λάθος;
οχι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 13:39:01 pm
θέλεις την Taylor για την z(x,y)
άρα
z(x,y)=z(1,1)+1*(dz/dx)(x-1)+1*(dz/dy)(y-1)
όπου z(1,1)=1
όπου dz/dx=-(dF/dx)/(dF/dz)
dz/dy=-(dF/dy)/(dF/dz)
άρα
z(x,y)=z(1,1)+1*(dz/dx)(x-1)+1*(dz/dy)(y-1)
όπου z(1,1)=1
όπου dz/dx=-(dF/dx)/(dF/dz)
dz/dy=-(dF/dy)/(dF/dz)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: cortex on June 14, 2014, 13:40:57 pm
σεπτέμβριος του 13 θέμα 2 το β ο taylor θα γίνει F(x,ψ,z)=F(1,1,1)+ 1/1! [dF/dx(1,1,1) (x-1) + dF/dψ(1,1,1) (ψ-1) + dF/dz(1,1,1) (z-1) ή κάνω κάποιο λάθος;
οχι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 13:48:06 pm
Για το αν είναι παραπάνω εξίσωση ορίζει πεπλεγμένη μορφή δείχνεις ότι dF/dz διάφορο του μηδέν F(σημειου που θες)=0 (που φυσικά θα ισχύει ) και να εχει συνεχεις μερικες παραγώγους.
Το γράφει άσκηση 1 λυμενες του ατρέα σελ 17 Κεφάλαιο 3
Το γράφει άσκηση 1 λυμενες του ατρέα σελ 17 Κεφάλαιο 3
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: NaVi.Mitsos on June 14, 2014, 13:50:40 pm
Παίδες βοήθεια για 5ο θέμα σεπεμβριου 2013 και 4ο θέμα ιούνη 2013 αν μπορεί κάποιος πιστεύω είναι πολύ αντιπροσωπευτικές θα βοηθήσουν όλους
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 14:48:35 pm
για τα θεματα Ξενου ή Ατρεα ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: NaVi.Mitsos on June 14, 2014, 14:52:25 pm
Ξένου ο ατρέας ίσως βάζζει λιγο διαφορετικά
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 16:36:55 pm
θεμα 3 ιουνιος 13 Ατρεας πως δειχνω οτι ειναι ασυμπιεστο ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 17:29:27 pm
θεμα 3 ιουνιος 13 Ατρεας πως δειχνω οτι ειναι ασυμπιεστο ?
(http://s27.postimg.org/iuidnin1r/IMG_20140614_172505.jpg) (http://postimg.org/image/iuidnin1r/)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 18:00:20 pm
ευχαριστω πολυ !!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 18:08:01 pm
4ο θέμα ιούνη 2013
(http://s13.postimg.org/vh9e2zumb/IMG_20140614_180302.jpg) (http://postimg.org/image/vh9e2zumb/)
(http://s13.postimg.org/qhbxv1ozn/IMG_20140614_180316.jpg) (http://postimg.org/image/qhbxv1ozn/)
(http://s13.postimg.org/vh9e2zumb/IMG_20140614_180302.jpg) (http://postimg.org/image/vh9e2zumb/)
(http://s13.postimg.org/qhbxv1ozn/IMG_20140614_180316.jpg) (http://postimg.org/image/qhbxv1ozn/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 18:11:15 pm
επισης το θεμα 6 Φεβρουαριου του 14 ξερει κανεις πως λυνεται ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 18:37:30 pm
επισης το θεμα 6 Φεβρουαριου του 14 ξερει κανεις πως λυνεται ?
(http://s4.postimg.org/qfhm2vpx5/IMG_20140614_183436.jpg) (http://postimg.org/image/qfhm2vpx5/)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 18:38:40 pm
αλανι ;)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 18:39:20 pm
σιγουρα ειναι σωστο ετσι ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Panos_Kanel on June 14, 2014, 18:42:29 pm
δε χρειάζεται να μπλέξεις με χyz , λύνεται πανεύκολα με τις ιδιότητες, το δεύτερο και το 3ο λύνονται χρησιμοποιώντας το πρώτο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 18:47:56 pm
δε χρειάζεται να μπλέξεις με χyz , λύνεται πανεύκολα με τις ιδιότητες, το δεύτερο και το 3ο λύνονται χρησιμοποιώντας το πρώτο
Ναι εννοειται και με ιδιοτητες :)απλά επειδή πολλοι νομίζω δεν κάθονται να τις μάθουν καλύτερο ειναι με μερικες, πιάνει φυσικα μια τάξη μεγέθους περισσότερο χωρο:) αλλα σε οδηγει σωστα:)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mrboombastic on June 14, 2014, 19:03:07 pm
Στα θέματα Φεβρουαρίου 2014, στο 1ο θέμα στο β΄ ερώτημα πως υπολογίζουμε προς ποια κατεύθυνση η παράγωγος παίρνει τη μέγιστη τιμή;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 19:18:25 pm
το θεμα 3β ατρεας 2013 ιουνιου πως λυνεται ?. Bγαινει αν απαλειψω το y χ=1 (νομιζω ειναι η προβολη της ευθειας) πως παραμετροποιηται αυτη ? :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 19:22:29 pm
Ατρεας Ιουνιος 2013
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Θεμα 3
ερωτημα β
Το επικαμπυλιο ειναι 2ου ειδους αφου ειναι της μορφης Pdx+Qdy+Rdz και η καμπυλη ειναι ανοιχτη αρα θα παω με ορισμο : ολοκληρωμα F(r(t))*r'(t)dt σωστα μεχρι εδω?
πως ομως θα παραμετροποιησω την καμπυλη αυτη? εχω κολλησει..help
Είχα κολλήσει κι εγώ εδώ. Στα downloads υπάρχουν οι σημειώσεις από τα μαθήματα του Ατρέα. Αν τις κατεβάσεις, στις σελίδες 120-121 του pdf θα δείς πως το κάνει.
Έπειτα το έλυσα όπως την άσκηση 4 από τις λυμένες του κεφαλαίου 7.
αυτα ελεγαν μερικα ποστ πιο πισω για την 3β που ρωταω
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 19:25:01 pm
Στα θέματα Φεβρουαρίου 2014, στο 1ο θέμα στο β΄ ερώτημα πως υπολογίζουμε προς ποια κατεύθυνση η παράγωγος παίρνει τη μέγιστη τιμή;
Βασική η παράγωγος ανά κατεύθυνση είναι το εσωτερικό γινόμενο της Δ(f(Po)*No (οπου Δ το ανάδελτα εννοω) όπου το πρωτό είναι η κλίση της βαθμωτής συνάρτησης,που είναι ένα διάνυσμα που μας δείχνει προς ποια κατεύθυνση πραγματοποιείται η μεγαλύτερη\(μέγιστη) μεταβολή. Το εσωτερικό γινόμενο ειναι ίσο με το μετρο του πρώτου επι το μετρο του δεύτερου επί το συνημίτονο της γωνίας του !!!άρα γίνεται μέγιστο όταν το συνημιτονο μοναδα αρα συνευθειακα αρα ιδια κατευθυσνη άρα το Νο(που ειναι το μοναδιαιο ) πρεπει αν δειχνει στην κατευθυνση του Δ(f(Po). Κάνω το Δ(f(Po) μοναδιάιο και έτσι βρίσκω την κατεύθυνση μέγιστης μεταβολής ενω η ελάχιστη ειναι προς το -(μοναδιαίο)Δ(f(Po) και αν ζηταει την τιμή αυτή ειναι ίση με το μέτρο του διανύσματος Δ(f(Po)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 20:14:07 pm
το θεμα 3β ατρεας 2013 ιουνιου πως λυνεται ?. Bγαινει αν απαλειψω το y χ=1 (νομιζω ειναι η προβολη της ευθειας) πως παραμετροποιηται αυτη ? :P
Το χ=1 και αντικαθιστώντας στις άλλες θα έχεις το y=2z-1
Θέτεις z=t y=2t-1 x=1 και αυτή είναι η παραμετροποίησή σου!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mrboombastic on June 14, 2014, 20:34:10 pm
Στα θέματα Φεβρουαρίου 2014, στο 1ο θέμα στο β΄ ερώτημα πως υπολογίζουμε προς ποια κατεύθυνση η παράγωγος παίρνει τη μέγιστη τιμή;
Βασική η παράγωγος ανά κατεύθυνση είναι το εσωτερικό γινόμενο της Δ(f(Po)*No (οπου Δ το ανάδελτα εννοω) όπου το πρωτό είναι η κλίση της βαθμωτής συνάρτησης,που είναι ένα διάνυσμα που μας δείχνει προς ποια κατεύθυνση πραγματοποιείται η μεγαλύτερη\(μέγιστη) μεταβολή. Το εσωτερικό γινόμενο ειναι ίσο με το μετρο του πρώτου επι το μετρο του δεύτερου επί το συνημίτονο της γωνίας του !!!άρα γίνεται μέγιστο όταν το συνημιτονο μοναδα αρα συνευθειακα αρα ιδια κατευθυσνη άρα το Νο(που ειναι το μοναδιαιο ) πρεπει αν δειχνει στην κατευθυνση του Δ(f(Po). Κάνω το Δ(f(Po) μοναδιάιο και έτσι βρίσκω την κατεύθυνση μέγιστης μεταβολής ενω η ελάχιστη ειναι προς το -(μοναδιαίο)Δ(f(Po) και αν ζηταει την τιμή αυτή ειναι ίση με το μέτρο του διανύσματος Δ(f(Po)
αα οκ! ευχαριστώ πολύ!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Marmotakos on June 14, 2014, 21:32:05 pm
στο θέμα 3 ιουνιος 13
το εμβαδον το βρίσκουμε με διπλό ολοκλήρωμα οκ?
το μήκος συνόρου???
το εμβαδον το βρίσκουμε με διπλό ολοκλήρωμα οκ?
το μήκος συνόρου???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 21:36:43 pm
2013 ΣΕΠ ΘΕΜΑ 5
(http://s27.postimg.org/e9l9smtv3/IMG_20140614_212428.jpg) (http://postimg.org/image/e9l9smtv3/)
(http://s27.postimg.org/e9l9smtv3/IMG_20140614_212428.jpg) (http://postimg.org/image/e9l9smtv3/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 21:56:52 pm
το θεμα 3β ατρεας 2013 ιουνιου πως λυνεται ?. Bγαινει αν απαλειψω το y χ=1 (νομιζω ειναι η προβολη της ευθειας) πως παραμετροποιηται αυτη ? :P
Το χ=1 και αντικαθιστώντας στις άλλες θα έχεις το y=2z-1
Θέτεις z=t y=2t-1 x=1 και αυτή είναι η παραμετροποίησή σου!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 22:03:38 pm
το θεμα 3β ατρεας 2013 ιουνιου πως λυνεται ?. Bγαινει αν απαλειψω το y χ=1 (νομιζω ειναι η προβολη της ευθειας) πως παραμετροποιηται αυτη ? :P
Το χ=1 και αντικαθιστώντας στις άλλες θα έχεις το y=2z-1
Θέτεις z=t y=2t-1 x=1 και αυτή είναι η παραμετροποίησή σου!
(http://s2.postimg.org/micudh8bp/IMG_20140614_220119.jpg) (http://postimg.org/image/micudh8bp/)
Στις πράξεις στο τέλος υπάρχει ενα λαθακι :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 22:17:39 pm
once again.. thank you
και οι πραξεις σου σωστες ηταν !
και οι πραξεις σου σωστες ηταν !
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 22:42:04 pm
στο 3γ ιουνης 13 ατρεας επειδη μου δινει εμβαδον θεωρω οτι dq/dx - dp/dy = 1 ??
βασικα πως βρισκω το εργο ?
βασικα πως βρισκω το εργο ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 22:53:51 pm
2013 θέμα 3 ιουνιος
Ελπίζω να είναι σωστό αν και το ολοκλήρωμα στο τέλος παρα έιναι δύσκολο άρα θα υπάρχει καλύτερος τρόπος...
(http://s30.postimg.org/ppnvgj4ml/IMG_20140614_224921.jpg) (http://postimg.org/image/ppnvgj4ml/)
(http://s30.postimg.org/un1g1n6lp/IMG_20140614_224933.jpg) (http://postimg.org/image/un1g1n6lp/)
Ελπίζω να είναι σωστό αν και το ολοκλήρωμα στο τέλος παρα έιναι δύσκολο άρα θα υπάρχει καλύτερος τρόπος...
(http://s30.postimg.org/ppnvgj4ml/IMG_20140614_224921.jpg) (http://postimg.org/image/ppnvgj4ml/)
(http://s30.postimg.org/un1g1n6lp/IMG_20140614_224933.jpg) (http://postimg.org/image/un1g1n6lp/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 23:07:41 pm
2013 3γ ιουνης ατρεας
(http://s4.postimg.org/3xojcwnp5/IMG_20140614_230530.jpg) (http://postimg.org/image/3xojcwnp5/)
(http://s4.postimg.org/3xojcwnp5/IMG_20140614_230530.jpg) (http://postimg.org/image/3xojcwnp5/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kourdisto_portokali on June 14, 2014, 23:23:32 pm
παιζει να ανεβασεις και ξενου σεπτ 13;;
στο πρωτο εχω κολλησει :/
στο πρωτο εχω κολλησει :/
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 23:27:37 pm
παιζει να ανεβασεις και ξενου σεπτ 13;;
στο πρωτο εχω κολλησει :/
1ο Θέμα ?στο πρωτο εχω κολλησει :/
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kourdisto_portokali on June 14, 2014, 23:30:31 pm
ναι
παιζει να ανεβασεις και ξενου σεπτ 13;;
στο πρωτο εχω κολλησει :/
1ο Θέμα ?στο πρωτο εχω κολλησει :/
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 23:35:12 pm
θεμα 4 α ιουνιος του 13 ατρεας ξερει κανεις τι κανουμε ? βρηκα σε ξενο βιβλιο ενα τυπο ριζα(1+f2x+f2y) για το εμβαδο αλλα βγαζει δυσκολα ολοκληρωματα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 14, 2014, 23:41:10 pm
ngv
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 14, 2014, 23:56:10 pm
στο υποερώτημα (α), για τυχόν επαληθεύσεις, η ροή έβγαινε 0 πάντως
Σε ποιά άσκηση?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2014, 23:57:27 pm
θεμα 4 α ιουνιος του 13 ατρεας ξερει κανεις τι κανουμε ? βρηκα σε ξενο βιβλιο ενα τυπο ριζα(1+f2x+f2y) για το εμβαδο αλλα βγαζει δυσκολα ολοκληρωματα
Καμια Ιδεα ?? :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 00:08:12 am
rw3
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 00:31:54 am
2013 ΣΕΠ ΘΕΜΑ 2 Ξενος
(http://s30.postimg.org/4alz5xzxp/IMG_20140615_002928.jpg) (http://postimg.org/image/4alz5xzxp/)
(http://s30.postimg.org/4alz5xzxp/IMG_20140615_002928.jpg) (http://postimg.org/image/4alz5xzxp/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 01:29:29 am
στο θεμα 2 Φεβρουαριος 14 (Α ομαδα) (Ατρεας) βρισκει κανεις 2 σαγματικα για να το επιβεβαιωσουμε ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabisI on June 15, 2014, 02:36:30 am
2013 Ιούνιος 4β Ατρέας
(http://s28.postimg.org/t8rzntds9/IMG_20140615_021901.jpg) (http://postimg.org/image/t8rzntds9/)
Η γωνία θ γιατί να είναι από π/2 μέχρι 3π/2?Το ημθ πρέπει να είναι <=0 ώστε και ψ<=0,άρα το θ είναι από π μέχρι 2π.Και βγαίνει 0 επίσης.(http://s28.postimg.org/t8rzntds9/IMG_20140615_021901.jpg) (http://postimg.org/image/t8rzntds9/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 02:43:54 am
2013 Ιούνιος 4β Ατρέας
(http://s28.postimg.org/t8rzntds9/IMG_20140615_021901.jpg) (http://postimg.org/image/t8rzntds9/)
Η γωνία θ γιατί να είναι από π/2 μέχρι 3π/2?Το ημθ πρέπει να είναι <=0 ώστε και ψ<=0,άρα το θ είναι από π μέχρι 2π.(http://s28.postimg.org/t8rzntds9/IMG_20140615_021901.jpg) (http://postimg.org/image/t8rzntds9/)
Ευτυχως βγαίνει το ίδιο αν λύσεις πιο κατω τα ολοκληρώματα!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 03:04:57 am
2014 θεμα 2 Φεβρουαριος (Α ομαδα) (Ατρεας)
(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kourdisto_portokali on June 15, 2014, 06:43:28 am
Ξενος Σεπτ. 13 θεμα 4)α)... αρκει να δειξουμε οτι το πεδιο ειναι συντηρητικο ;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 12:05:30 pm
2013 θεμα 4 α ιουνιος
(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
δε νομίζω πως μπορείς να πάρεις για πάρεις από 2sqrt(2) μέχρι 3 γιατί το χωρίο δεν είναι κανονικό. υπολογίζεις τον εξωτερικό και τον εσωτερικό κύκλο χωριστά και τα αφαιρείς.(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 12:06:22 pm
2014 θεμα 2 Φεβρουαριος (Α ομαδα) (Ατρεας)
(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
τελικα ειναι του 13 ατρεας
αλλα ευχαριστουμε και παλι !!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: dkitsios on June 15, 2014, 12:21:05 pm
Exeis kaneis lush gia to thema 2b iouniou 13 atrea??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 12:29:23 pm
Ξενος Σεπτ. 13 θεμα 4)α)... αρκει να δειξουμε οτι το πεδιο ειναι συντηρητικο ;
Ναι βγαζεις τρεις εξισωσεις με μερικες παραγώγους της f και από ότι θυμάμαι είναι εύκολη η λύση με πράξεις με αυτές.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 12:45:26 pm
2013 θεμα 4 α ιουνιος
(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
δε νομίζω πως μπορείς να πάρεις για πάρεις από 2sqrt(2) μέχρι 3 γιατί το χωρίο δεν είναι κανονικό. υπολογίζεις τον εξωτερικό και τον εσωτερικό κύκλο χωριστά και τα αφαιρείς.(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 12:47:48 pm
το ΄΄ιδιο ισχύει και τα τριπλά ολοκληρώματα. πρέπει πάντα να παίρνεις τα χωρία σου να είναι κανονικά.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 12:54:34 pm
το ΄΄ιδιο ισχύει και τα τριπλά ολοκληρώματα. πρέπει πάντα να παίρνεις τα χωρία σου να είναι κανονικά.
Άρα ακολουθουμε αυτο !!! λαθος η λύση μου να την κατεβάσω!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabisI on June 15, 2014, 13:01:30 pm
2014 θεμα 2 Φεβρουαριος (Α ομαδα) (Ατρεας)
(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
Για το (1/2,-1,-1) γιατί να πούμε ότι είναι σαγματικό?Ο πίνακας ΔΕΝ είναι μικτά προσημασμένος,αφού για να ήταν από τη θεωρία θα έπρεπε να υπάρχουν τουλάχιστον δύο αριθμοί στην κύρια διαγώνιο με αντίθετα πρόσημα.Εδώ είναι και τα τρία αρνητικά.Άρα η σωστή απάντηση λογικά θα είναι δεν ξέρουμε τι είναι το σημείο αυτό.(http://s7.postimg.org/4h6zjp113/IMG_20140615_030057.jpg) (http://postimg.org/image/4h6zjp113/)
(http://s7.postimg.org/i9lefbrsn/IMG_20140615_030121.jpg) (http://postimg.org/image/i9lefbrsn/)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 13:05:19 pm
πρεπει παντα να ισχυει αυτο με την διαγωνιο(να εχουμε 2 αριθμους με διαφορετικο προσημο ? ) ωστε να ειναι σαγματικο (δεν ειμαι και σιγουρος ρωταω)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabisI on June 15, 2014, 13:09:26 pm
πρεπει παντα να ισχυει αυτο με την διαγωνιο(να εχουμε 2 αριθμους με διαφορετικο προσημο ? ) ωστε να ειναι σαγματικο (δεν ειμαι και σιγουρος ρωταω)
Ναι,το γράφει στη θεωρία στο pdfTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 13:29:32 pm
Πάντως και στο wolfram αν το βάλεις αυτο βγάζει μονο ... Ολα εξαρτονται απο τον fxx ,το διπλό πίνακα και τριπλό όχι απο τις διαγωνίους τους .
- + - μέγιστο
+ + + ελαχιστο
Είπα σαγματικο γιατί συνήθως για το δεν ξέρουμε θέλει να βγει κάποια ίση με μηδέν ( εδώ μπορεί να κάνω λάθος φυσικά )
- + - μέγιστο
+ + + ελαχιστο
Είπα σαγματικο γιατί συνήθως για το δεν ξέρουμε θέλει να βγει κάποια ίση με μηδέν ( εδώ μπορεί να κάνω λάθος φυσικά )
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 13:40:06 pm
θεμα 4α 2014 ατρεας πως βγαινει ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: BabisI on June 15, 2014, 13:51:21 pm
Πάντως και στο wolfram αν το βάλεις αυτο βγάζει μονο ... Ολα εξαρτονται απο τον fxx ,το διπλό πίνακα και τριπλό όχι απο τις διαγωνίους τους .
- + - μέγιστο
+ + + ελαχιστο
Είπα σαγματικο γιατί συνήθως για το δεν ξέρουμε θέλει να βγει κάποια ίση με μηδέν ( εδώ μπορεί να κάνω λάθος φυσικά )
Τι να πω,εγώ αναφέρω αυτό που έχει στη θεωρία,σελ. 11-12 από κεφ. 3.Δίνει ορισμό του μικτά προσημασμένου και μετά λέει αν είναι μικτά τότε είναι σαγματικό.Και μετά στις παρατηρήσεις λέει ότι αν δεν είναι ούτε θετικά ούτε αρνητικά ούτε μικτά τότε δεν μπορούμε να αποφανθούμε.- + - μέγιστο
+ + + ελαχιστο
Είπα σαγματικο γιατί συνήθως για το δεν ξέρουμε θέλει να βγει κάποια ίση με μηδέν ( εδώ μπορεί να κάνω λάθος φυσικά )
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 14:04:55 pm
d44h
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 14:45:51 pm
θεμα 4α 2014 ατρεας πως βγαινει ?
καμι ιδεα ?Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 14:57:26 pm
Θεμα 2β ατρεας 2013 ιουνης ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 15:06:19 pm
fse
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Panos_Kanel on June 15, 2014, 15:15:25 pm
Ναι 8π βρήκα και γω με πολικές.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Panos_Kanel on June 15, 2014, 15:18:09 pm
Έχει βγάλει κανείς το 1β του Ιουνίου 13 ατρέα; αυτό με τις (μ)πλεγμένες
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 15:38:35 pm
Θέμα 4α ατρέας 2014 έχεις την έλλειψη 4χ^2+ψ^2=16 ή χ^2/2^2 + ψ^2/4^2=1 έχεις χωρίο κανονικό ως προς ψ παίρνεις χωρίο Τ={ -2≤x≤2 και -2sqrt(4-x^2)≤ψ≤2sqrt(4-x^2)} ε και βγαίνει το ολοκλήρωμα με απλές πράξεις μετά ίσο με 8π (με επιφύλαξη για το νούμερο)
το ψ γιατι ειναι -2sqrt(4-x^2)≤ψ≤2sqrt(4-x^2) μπορεις να το εξηγησεις λιγο πιο αναλυτικα ? ( μηπως μες την ριζα εχεις 16-χ^2 ??) :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 16:26:38 pm
rwe
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 16:38:11 pm
4χ^2+ψ^2=16 => ψ^2=4(4-χ^2) => ψ=+/- sqrt(4(4-χ^2))=+/- 2sqrt(4-x^2) τα δύο ημισφαίρια της έλλειψης
βγαινει ενα δυσκολο ολοκληρωμα και το αποτελεσμα του ειναι 0 (τουλαχιστον τοσο βρισκω ) ειναι σωστο εμβαδον = 0 ? μαλλον οχι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 16:41:12 pm
werw
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 16:48:02 pm
το χωρίο είναι κανονικό ως προς ψ, δηλαδή οποιαδήποτε παράλληλη στον ψ'ψ ευθεία τέμνει το χωρίο μόνο σε δύο σημεία
άρα κοιτάς από που μπαίνει και από που βγαίνει μία τέτοια ευθεία
μπαίνει από το κάτω ημισφαίριο της έλλειψης ψ=-2sqrt(4-x^2) και βγαίνει από το πάνω ημισφαίριο της έλλειψης ψ=2sqrt(4-x^2)
μπορείς να κάνεις είτε μετασχηματισμό σε πολικές για να το βρεις, είτε να προχωρήσεις και να υπολογίσεις το ολοκλήρωμα από -2 έως 2 του 4sqrt(4-x^2)dx το οποίο ισούται με 4επί2π=8π
αν πάρεις πολικές από την αρχή θέσε χ=4cosθ και ψ=sinθ με r=4 και βγαίνει διαφορετικά
άρα κοιτάς από που μπαίνει και από που βγαίνει μία τέτοια ευθεία
μπαίνει από το κάτω ημισφαίριο της έλλειψης ψ=-2sqrt(4-x^2) και βγαίνει από το πάνω ημισφαίριο της έλλειψης ψ=2sqrt(4-x^2)
μπορείς να κάνεις είτε μετασχηματισμό σε πολικές για να το βρεις, είτε να προχωρήσεις και να υπολογίσεις το ολοκλήρωμα από -2 έως 2 του 4sqrt(4-x^2)dx το οποίο ισούται με 4επί2π=8π
αν πάρεις πολικές από την αρχή θέσε χ=4cosθ και ψ=sinθ με r=4 και βγαίνει διαφορετικά
σωστος εκανα αριθμητικο λαθος εγω !!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 17:10:50 pm
καποιος να μου πει τι βρηκε στην 3 ατρεα 2014 για να επαληθευσω ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: mitsoos on June 15, 2014, 17:15:07 pm
Θεματα Ξενου σεπτεμβρίου 2ο θεμα το α) τι ακριβως ζηταει ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 17:15:25 pm
Θεμα 2β ατρεας 2013 ιουνης ??
αυτο μ εμεινε ..... καποιος ?? :)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 17:17:13 pm
τελικά στο θέμα 2 του 2014 του Ατρέα τι ακρότατα έχω;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: taras on June 15, 2014, 17:35:32 pm
Θεματα Ξενου σεπτεμβρίου 2ο θεμα το α) τι ακριβως ζηταει ?
Aπάντηση:
Για το αν είναι παραπάνω εξίσωση ορίζει πεπλεγμένη μορφή δείχνεις ότι dF/dz διάφορο του μηδέν F(σημειου που θες)=0 (που φυσικά θα ισχύει ) και να εχει συνεχεις μερικες παραγώγους.
Το γράφει άσκηση 1 λυμενες του ατρέα σελ 17 Κεφάλαιο 3
Το γράφει άσκηση 1 λυμενες του ατρέα σελ 17 Κεφάλαιο 3
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 17:36:17 pm
το θεμα 1 α Ατρεας 2013 πως λυνεται ?? ειναι παραλλαγη της κλασικης ασκησης : να βρεθει η παραγωγος κατα την κατευθηνση κλπ κλπ.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Ancient on June 15, 2014, 17:40:20 pm
2013 θεμα 4 α ιουνιος
(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
δε νομίζω πως μπορείς να πάρεις για πάρεις από 2sqrt(2) μέχρι 3 γιατί το χωρίο δεν είναι κανονικό. υπολογίζεις τον εξωτερικό και τον εσωτερικό κύκλο χωριστά και τα αφαιρείς.(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
ένα σχεδόν ίδιο θέμα ο ξένος το έκανε με αυτόν τον τρόπο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 17:58:30 pm
2013 θεμα 4 α ιουνιος
(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
δε νομίζω πως μπορείς να πάρεις για πάρεις από 2sqrt(2) μέχρι 3 γιατί το χωρίο δεν είναι κανονικό. υπολογίζεις τον εξωτερικό και τον εσωτερικό κύκλο χωριστά και τα αφαιρείς.(http://s14.postimg.org/m7kduu1r1/IMG_20140614_235447.jpg) (http://postimg.org/image/m7kduu1r1/)
ένα σχεδόν ίδιο θέμα ο ξένος το έκανε με αυτόν τον τρόπο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 18:13:02 pm
fse
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 18:14:57 pm
Στο Θέμα 1(α) από τα θέματα του Ατρέα του Ιουνίου 2013 το gradf(Po) ισούται με (1-sqrt(17),1+sqrt(17));
εγώ βρήκα (1-sqrt(2),1=sqrt(2)) Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 18:22:12 pm
και με ποια διαδικασια το βρισκετε ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 18:28:44 pm
και με ποια διαδικασια το βρισκετε ?
μπορώ να το ανεβάσω σε φωτογραφία εάν μπορεί να μου πει κάποιος πώς να το κάνω :PTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 18:30:02 pm
d5h
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 18:31:30 pm
και με ποια διαδικασια το βρισκετε ?
μπορώ να το ανεβάσω σε φωτογραφία εάν μπορεί να μου πει κάποιος πώς να το κάνω :PTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Επικο Burger on June 15, 2014, 18:39:20 pm
Toso βγαινει :D 1-sqrt2 , 1+sqrt2
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 18:39:39 pm
αφού η συνάρτηση είναι διαφορίσιμη θα πάρεις διαφορικό f(po) στην κατεύθυνση του α ισούται με α μοναδιαίο εσωτερικό γινόμενο μερική παράγωγος στο po και |μερική στο Po|=6 και έχει δύο εξισώσεις για δύο αγνώστους fx και fy
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 15, 2014, 18:49:25 pm
αφού η συνάρτηση είναι διαφορίσιμη θα πάρεις διαφορικό f(po) στην κατεύθυνση του α ισούται με α μοναδιαίο εσωτερικό γινόμενο μερική παράγωγος στο po και |μερική στο Po|=6 και έχει δύο εξισώσεις για δύο αγνώστους fx και fy
γιατι |μερικη στο Ρο | = 6 και οχι -ριζα(6) ?Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 18:51:54 pm
hrd
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: adna on June 15, 2014, 18:54:44 pm
οι δύο σχέσεις που έχεις είναι:
επειδή f διαφορίσιμη => κατευθυνόμενη ως προς το α0=gradf=(fx,fy)*a0 βγάζεις fx+fy=2
ακόμη -|gradf(Po)|=-sqrt(6) και από εδώ βγάζεις fx^2+fy^2=6
ναι αυτό εννοούσα.επειδή f διαφορίσιμη => κατευθυνόμενη ως προς το α0=gradf=(fx,fy)*a0 βγάζεις fx+fy=2
ακόμη -|gradf(Po)|=-sqrt(6) και από εδώ βγάζεις fx^2+fy^2=6
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 18:59:48 pm
ter
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kthulu on June 15, 2014, 20:59:53 pm
"Να βρεθούν οι ισοσταθμικές επιφάνεις της συναρτησης f"
Ποιά ακριβώς είναι η μεθοδολογία εδω;
Ποιά ακριβώς είναι η μεθοδολογία εδω;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 21:06:55 pm
yer
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Panos_Kanel on June 15, 2014, 21:18:17 pm
για το ίδιο θέμα το (β) υποερώτημα, έχετε καμιά ιδέα;
μια πρώτη σκέψη ήταν ότι u=x-y και v=x+y, αλλά δεν μου φαίνεται τόσο λογικό
μια πρώτη σκέψη ήταν ότι u=x-y και v=x+y, αλλά δεν μου φαίνεται τόσο λογικό
ναι αυτά θέτεις, μετά παίρνεις το διαφορικό της f, βρίσκεις τα du,dv ξεχωριστά, τα αντικαθιστάς και επίσης όπου dy βάζεις y'(x)dx και λύνεις την εξίσωση
βρήκα y'(x)= (fu+fv) / (fu-fv)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 21:55:20 pm
he4
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Panos_Kanel on June 15, 2014, 22:43:35 pm
du=dx-dy = dx-y'(x)dx
dv=dx+dy= dx+y'(x)dx
f(u,v)=0 -> fudu+fvdv=0 -> fu(dx(1-y'(x))+fv(dx(1+y'(x))=0
κοινό παράγοντα dx και μετά είναι απλές οι πράξεις.
dv=dx+dy= dx+y'(x)dx
f(u,v)=0 -> fudu+fvdv=0 -> fu(dx(1-y'(x))+fv(dx(1+y'(x))=0
κοινό παράγοντα dx και μετά είναι απλές οι πράξεις.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meh on June 15, 2014, 22:49:41 pm
te4
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vlassis on June 15, 2014, 23:14:43 pm
Στα θεματα 2014 στο θεμα 5, πως βρισκουμε τη γωνια???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: NaVi.Mitsos on June 15, 2014, 23:16:41 pm
paidia an theloume na vroume to mikos kampilis kai vroume oti to panw akro tou oloklirwmatos einai thetiko kai mikroterou tou katw thetikou akrou diladi me liga logia to epikampilio einai <0 tote pernoume tin apoliti timi tou gt theloume mikos?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 15, 2014, 23:49:24 pm
paidia an theloume na vroume to mikos kampilis kai vroume oti to panw akro tou oloklirwmatos einai thetiko kai mikroterou tou katw thetikou akrou diladi me liga logia to epikampilio einai <0 tote pernoume tin apoliti timi tou gt theloume mikos?
ΝαιTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Επικο Burger on June 16, 2014, 00:14:18 am
Ρε παιδια μην γραφετε με greeklish, μας βγαινουν τα ματια.
paidia an theloume na vroume to mikos kampilis kai vroume oti to panw akro tou oloklirwmatos einai thetiko kai mikroterou tou katw thetikou akrou diladi me liga logia to epikampilio einai <0 tote pernoume tin apoliti timi tou gt theloume mikos?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Utrion on June 16, 2014, 00:30:02 am
Στα θεματα 2014 στο θεμα 5, πως βρισκουμε τη γωνια???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
Παραγωγίζουμε την r(t) (καθε διασταση χωριστα) και αυτο ειναι το διανυσμα της εφαπτομένης
Το διάνυσμα του z=(0,0,1)
To εσωτερικό τους γινόμενο είναι r΄(t)*zo=μετρο(r΄(t))*1*cosφ και βρίσκεις το φ
Συντηρητικό είναι όταν η rotF=(0,0,0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vlassis on June 16, 2014, 00:42:36 am
ωραιος :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on August 22, 2014, 17:05:49 pm
Στα downloads μπορείτε πλέον να βρείτε λύσεις θεμάτων Ιουνίου 2014 και των δύο με κάθε επιφύλαξη για λάθη.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pentium4 on August 22, 2014, 17:06:12 pm
μόλις ανέβηκαν οι λύσεις του Ιουνίου. Επειδή δε μπορώ να χαζεύω συνεχώς το τόπικ ,αν υπάρχει διαπιστωμένα κάποιο λάθος μου στέλνετε πμ για να το γράψω στην περιγραφή του αρχείου στα downloads !
με πρόλαβες χαχα
με πρόλαβες χαχα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: football on September 02, 2014, 18:49:50 pm
Καποιος αν μπορει να πει για το 3ο θεμα απο σεπτεμβριο 2013 εκεινο με την θερμοκρασια...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kthulu on September 05, 2014, 23:06:18 pm
Σημειώσεις Ατρέα-> Επιφανειακά Ολοκλ -> Λυμενη άσκηση 4 :
Στην εξέταση μπορούμε να θεωρήσουμε δεδομένο το εμβαδόν E(D) του ημισφαιρίου;
Στην εξέταση μπορούμε να θεωρήσουμε δεδομένο το εμβαδόν E(D) του ημισφαιρίου;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Reiner on September 08, 2014, 21:55:56 pm
Ξέρει κανείς στις λύσεις των θεμάτων του Ιουνίου 2014 στο πρώτο θέμα με τις ισοσταθμικές επιφάνειες, γιατί όταν c=0 η εξίσωση περιγράφει σημείο και όχι κωνική επιφάνεια;
Η εξίσωση της κωνικής επιφάνειας δεν είναι xˆ2/aˆ2 + ψˆ2/bˆ2 + zˆ2/cˆ2 = 0
Η εξίσωση της κωνικής επιφάνειας δεν είναι xˆ2/aˆ2 + ψˆ2/bˆ2 + zˆ2/cˆ2 = 0
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 08, 2014, 22:30:11 pm
Άθροισμα τετραγώνων 0 τι συνεπάγεται;;
Μια εκφυλισμένη κωνική, αν και το ελλειψοειδές μοιάζει πιο πιθανό ισως αλλα καλύτερα ας πούμε σημειο
Μια εκφυλισμένη κωνική, αν και το ελλειψοειδές μοιάζει πιο πιθανό ισως αλλα καλύτερα ας πούμε σημειο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: electric67 on September 10, 2014, 09:31:34 am
στα θεματα του Φεβρουαριου 2014 που ζητάει τις ισοσταθμικές επιφάνειες της f(x,y,z)=4x^2 - y^2 + 4z^2 +12 , τι ακριβώς πρέπει να κάνουμε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vlassis on September 10, 2014, 13:40:37 pm
Νομιζω βαζεις f(x,y,z) = c και παιρνεις περιπτωσεις αναλογα με το c ( >0, <0, =0 ), λες τι ειναι η επιφανεια!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kthulu on September 12, 2014, 18:31:08 pm
Θεματα Ξενου Σεπτέμβριος 2013 Θεμα 2.γ:
Εδώ χρησιμοποιούμε καθόλου τη πλεγμένη z ή τα βρισκουμε κατ'ευθείαν απο την F;
Εδώ χρησιμοποιούμε καθόλου τη πλεγμένη z ή τα βρισκουμε κατ'ευθείαν απο την F;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: electric67 on September 12, 2014, 19:23:49 pm
το ανάδελτα σαν διάνυσμα δεν συμπεριφέρεται; δηλαδή αν έχω μικτο γινόμενο, ισχύει η ακόλουθη ισότητα;
( F x G) * ανάδελτα = (αναδελτα x F ) * G , με βάση την ιδιότητα του μικτου γινομένου (a,b,c)=(b,c,a)=(c,a,b) ;
οπου F,G διανυσματικά πεδία
( F x G) * ανάδελτα = (αναδελτα x F ) * G , με βάση την ιδιότητα του μικτου γινομένου (a,b,c)=(b,c,a)=(c,a,b) ;
οπου F,G διανυσματικά πεδία
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2014, 12:10:13 pm
το τριπλο ολοκληρωμα του dxdydz οταν εχω σφαιρα x^2 + y^2 + z^2 = a^2 με τι ισουται ?
τα μετατρεπω σε πολικες συντεταγμενες ??
τα μετατρεπω σε πολικες συντεταγμενες ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilis94 on September 13, 2014, 12:40:54 pm
το τριπλο ολοκληρωμα του dxdydz οταν εχω σφαιρα x^2 + y^2 + z^2 = a^2 με τι ισουται ?
τα μετατρεπω σε πολικες συντεταγμενες ??
τα μετατρεπω σε πολικες συντεταγμενες ??
Αν η συνάρτηση είναι f(x,y,z)=1 τότε το τριπλό δίνει τον όγκο του στερεού μέσα στο οποίο ολοκληρώνεις. Οπότε μπορείς κατευθείαν ή τυπο σφαίρας 4/3 *π *α^3 ή αν μετασχηματίσεις σε σφαιρικές θα πάρεις το ίδιο.
Γενικά όταν έχεις να ολοκληρώσεις σε σφαίρα, κάνεις μετασχηματισμό σε σφαιρικές συνήθως. Πρέπει να βολεύει και λίγο η συνάρτηση βέβαια...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2014, 12:48:29 pm
ωραιος , ευχαριστω !
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: night.atk on September 13, 2014, 20:11:36 pm
Στα Θεματα Φεβρουαριου 2014 στο 7ο θέμα που ζητάει το έργο του πεδίου,θελει να υπολογίσουμε το επικαμπύλιο β΄ είδους της F επι του συνόρου του φραγμένου χωρίου μεταξύ 2 σημείων ή κατι αλλο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 13, 2014, 22:28:02 pm
Στα θεματα 2014 στο θεμα 5, πως βρισκουμε τη γωνια???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
+ ποτε ενα πεδιο ειναι συντηρητικο ???
Παραγωγίζουμε την r(t) (καθε διασταση χωριστα) και αυτο ειναι το διανυσμα της εφαπτομένης
Το διάνυσμα του z=(0,0,1)
To εσωτερικό τους γινόμενο είναι r΄(t)*zo=μετρο(r΄(t))*1*cosφ και βρίσκεις το φ
Συντηρητικό είναι όταν η rotF=(0,0,0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 13, 2014, 22:32:34 pm
Ξέρει κανείς στις λύσεις των θεμάτων του Ιουνίου 2014 στο πρώτο θέμα με τις ισοσταθμικές επιφάνειες, γιατί όταν c=0 η εξίσωση περιγράφει σημείο και όχι κωνική επιφάνεια;
Η εξίσωση της κωνικής επιφάνειας δεν είναι xˆ2/aˆ2 + ψˆ2/bˆ2 + zˆ2/cˆ2 = 0
http://www.wolframalpha.com/input/?i=x*x-y*y%2B4*z*z%3D0 (http://www.wolframalpha.com/input/?i=x*x-y*y%2B4*z*z%3D0)Η εξίσωση της κωνικής επιφάνειας δεν είναι xˆ2/aˆ2 + ψˆ2/bˆ2 + zˆ2/cˆ2 = 0
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 13, 2014, 22:39:53 pm
Για να είναι συντηρητικό δεν πρεπει να υπαρχει και μια f τετοια ωστε gradf = F ???
Άμα ο τόπος είναι απλά συνεκτικός, τότε αρκεί απλά να είναι αστρόβιλο και να έχει συνεχείς μερικές παραγώγους.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 13, 2014, 22:46:07 pm
Για να είναι συντηρητικό δεν πρεπει να υπαρχει και μια f τετοια ωστε gradf = F ???
Άμα ο τόπος είναι απλά συνεκτικός, τότε αρκεί απλά να είναι αστρόβιλο και να έχει συνεχείς μερικές παραγώγους.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 13, 2014, 22:48:55 pm
Στα Θεματα Φεβρουαριου 2014 στο 7ο θέμα που ζητάει το έργο του πεδίου,θελει να υπολογίσουμε το επικαμπύλιο β΄ είδους της F επι του συνόρου του φραγμένου χωρίου μεταξύ 2 σημείων ή κατι αλλο?
Ναι. Πέρνεις green και για να βρείς το χωρίο μετασχηματίζεις x=sqrt2*ρ*συνθ, y=ρ*ημθ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 13, 2014, 23:21:38 pm
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kthulu on September 13, 2014, 23:28:13 pm
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Ο ρυθμός μετάβολης μίας συνάρτησης F γίνεται μεγίστος στην κατέυθυνση του (αναδελτα)F(Ρ) με τιμή |(αναδελτα)F(Ρ)| Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 13, 2014, 23:32:48 pm
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Ο ρυθμός μετάβολης μίας συνάρτησης F γίνεται μεγίστος στην κατέυθυνση του (αναδελτα)F(Ρ) με τιμή |(αναδελτα)F(Ρ)| Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Kthulu on September 13, 2014, 23:48:25 pm
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Ο ρυθμός μετάβολης μίας συνάρτησης F γίνεται μεγίστος στην κατέυθυνση του (αναδελτα)F(Ρ) με τιμή |(αναδελτα)F(Ρ)| Σωστά . Αν ρωτούσε ελάχιστος βάζουμε -(μείον) και στο δ/σμα και στην απόλυτη τιμη του δ/σματος κλισης που είπαμε παραπάνω.
Δες και μόνος σου σημειώσεις ατρέα κεφάλαιο 2 λυμένη ασκηση 5
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 01:11:54 am
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Ο ρυθμός μετάβολης μίας συνάρτησης F γίνεται μεγίστος στην κατέυθυνση του (αναδελτα)F(Ρ) με τιμή |(αναδελτα)F(Ρ)| Σωστά . Αν ρωτούσε ελάχιστος βάζουμε -(μείον) και στο δ/σμα και στην απόλυτη τιμη του δ/σματος κλισης που είπαμε παραπάνω.
Δες και μόνος σου σημειώσεις ατρέα κεφάλαιο 2 λυμένη ασκηση 5
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 01:41:37 am
ετσι οπως το χει λυσει μια κοπελα στα downloads ειναι λαθος ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 01:48:39 am
ετσι οπως το χει λυσει μια κοπελα στα downloads ειναι λαθος ?
μαλλον σωστο ειναι γιατί η ασκηση λεει: "προς ποια κατευθυνση ο ρυθμος μεταβολής γίνεται μεγιστος"
Ενώ στις ασκήσεις του ατρεα(ασκ 5 απο λυμενες κεφ 2) λεει: "Ποια είναι η
κατεύθυνση πάνω στην οποία παρατηρείται η ελάχιστη τιµή της κλίσης"
οποτε θα ελεγα στου Ξενου ειναι gradf * Vo εφόσον ζηταει ρυθμο μεταβολής
και στου ατρεα απλα παιρνει το gradf μονο γιατι ζηταει κλίση κ οχι ρυθμο μεταβολής
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 01:52:00 am
μπορεί να μου εξηγήσει κάποιος από την ασκηση 2 το ερωτημα β εκει που λεει για μεγιστο ρυθμο μεταβολής? Ξενος Ιούνιος 14 ^rotate^
Το θεμα θελει και αιτιολογηση και δεν ξερω τι πρεπει να απαντησω! γνωρίζει κάποιος??? Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: alexpaxi on September 14, 2014, 04:27:21 am
στο 4ο θεμα του ιουνιου του 2014 στο Ξενο Β ομαδα στο β ερωτημα εχει λαθος στο διανυσματικο πεδιο G?γιατι δεν μου βγαινει divG=0 για να πω οτι προερχεται απο διανυσματικο δυναμικο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 11:37:59 am
στο 4ο θεμα του ιουνιου του 2014 στο Ξενο Β ομαδα στο β ερωτημα εχει λαθος στο διανυσματικο πεδιο G?γιατι δεν μου βγαινει divG=0 για να πω οτι προερχεται απο διανυσματικο δυναμικο.
μαλλον καπου εχεις λαθος, γιατι 0 βγαινει... Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: akisseleo on September 14, 2014, 12:47:16 pm
Στο θέμα Ιουν 2014 του Ατρέα στο 2α έχει λάθος.Στο διπλό ολοκλήρωμα ολοκληρώνει από 0 έως 2(που είναι το χ) και στο μέσα ολοκλήρωμα έχει συναρτήσεις που περιέχουν το y.Με αυτόν τον τρόπο όταν κάνεις την ολοκλήρωση θα έχεις και Χ και Υ όταν κάνεις το μέσα ολοκλήρωμα. ΠΟΥ ΕΊΝΑΙ ΛΑΘΟΣ. Τα άκρα του μέσα ολοκληρώματος πρέπει να λύνονται ως προς την μεταβλητή που θα ολοκληρώσεις πρώτη ώστε όταν αντικαθιστάς τις τιμές(συναρτήσεις) των μέσα ορίων να μένει μόνο η έξω μεταβλητή στο έξω ολοκλήρωμα και να βγάζεις αποτέλεσμα αριθμό!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: τεκίλα_αλάτι_λεμόνι on September 14, 2014, 13:01:25 pm
Παιδεία μπορεί κάποιος που έχει λύσει τα θέματα του Ξένου Σεπτέβριος 2013 να τα ανεβάσει;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 13:07:52 pm
Παιδεία μπορεί κάποιος που έχει λύσει τα θέματα του Ξένου Σεπτέβριος 2013 να τα ανεβάσει;
+1 ^beg^Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 14, 2014, 13:29:36 pm
Παιδεία μπορεί κάποιος που έχει λύσει τα θέματα του Ξένου Σεπτέβριος 2013 να τα ανεβάσει;
+1 ^beg^+1
ειδικά το 1ο θέμα δε μου βγαινει με τίποτα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: akisseleo on September 14, 2014, 13:30:11 pm
μία πιο σωστή λύση για το θέμα Ιουν 2014 του Ατρέα 2α, από αυτό που έχει στο νταουνλοαντ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: football on September 14, 2014, 14:02:32 pm
Θεματα Ξενου Σεπτέμβριος 2013 Θεμα 2.γ:
Εδώ χρησιμοποιούμε καθόλου τη πλεγμένη z ή τα βρισκουμε κατ'ευθείαν απο την F;
Εδώ χρησιμοποιούμε καθόλου τη πλεγμένη z ή τα βρισκουμε κατ'ευθείαν απο την F;
+1
και για το 2α ας εξηγήσει όποιος μπορεί!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: night.atk on September 14, 2014, 14:53:08 pm
Για το 8ο θεμα Φεβρουριου κανουμε χρηση του θεωρηματος Gauss? Αν ναι μετα πως υπολογιζουμε το 3πλο που προκυπτει? Μπερδευομαι στα ορια
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: theofilos on September 14, 2014, 14:58:35 pm
απο τα θεματα του ξενου ιουνιος 2014, το 2 θεμα με τα ακροτατα , μπορει να παραθεσει καποιος μια συντομη λυση η τουλαχιστων τα σημεια που ειναι υποψηφια για ακροτατα εκτος το (0,0)...δεν βγαζω ακρη
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 14, 2014, 15:00:32 pm
απο τα θεματα του ξενου ιουνιος 2014, το 2 θεμα με τα ακροτατα , μπορει να παραθεσει καποιος μια συντομη λυση η τουλαχιστων τα σημεια που ειναι υποψηφια για ακροτατα εκτος το (0,0)...δεν βγαζω ακρη
ειναι το (0,0) που βγαινει σαγματικό
και το (τριτη ρίζα του 4, τρίτη ρίζα του -2) που βγαινει τοπικό ελάχιστο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 14, 2014, 15:02:52 pm
Παιδεία μπορεί κάποιος που έχει λύσει τα θέματα του Ξένου Σεπτέβριος 2013 να τα ανεβάσει;
+1000!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 16:20:06 pm
για το πρωτο θεμα σεπτ 13 το ελυσα ως εξης...
εθεσα x+y = u αρα
δz/δx = ( δz/ δu ) * (δu/δx ) το σπαω δλδ για να εμφανισω το u και δu/δy = 1 αρα τελικα ισουται με δf/δu + x * δg/δu...
και η δευτερη παραγωγος με την παραγωγο αυτου που βρηκα πανω ως προς δu
ομοιως κανω και τα υπολοιπα...
αν βλεπετε κανα λαθος στον τροπο γενικα πειτε μου .. !
εθεσα x+y = u αρα
δz/δx = ( δz/ δu ) * (δu/δx ) το σπαω δλδ για να εμφανισω το u και δu/δy = 1 αρα τελικα ισουται με δf/δu + x * δg/δu...
και η δευτερη παραγωγος με την παραγωγο αυτου που βρηκα πανω ως προς δu
ομοιως κανω και τα υπολοιπα...
αν βλεπετε κανα λαθος στον τροπο γενικα πειτε μου .. !
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 16:58:18 pm
θεμα 2 σεπτ 13 ( ξενου ) το λυσε κανεις ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airpap on September 14, 2014, 16:59:35 pm
θεματα ιουνιου 2013
θεμα 3 το β! καποια βοηθεια "εκκίνησης" ? :P
θεμα 3 το β! καποια βοηθεια "εκκίνησης" ? :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 14, 2014, 17:25:54 pm
για το α)
αν στη F θέσεις όπου x = y = 1 δηλαδή το σημείο (1,1) θα σου βγει z^3 + z - 2 = 0 και στο τέλος λέει ώστε z(1,1) = 1 ή z = 1 το οποίο επαληθεύεται.
το ότι ορίζει σε πεπλεγμένη μορφή συνάρτηση z = z(x,y) το αποδεικνύεται από τους τύπους:
Zx = - Fx / Fz και Zy = - Fy / Fz τα οποία στο σημείο (1,1) πρέπει να βγουν διάφορα του μηδενός για το σημείο (1,1,1)
και μετά για το
γ) το εφαπτόμενο δίνεται από τον τύπο: Z - 1 = Zx(1,1,1) ( x - 1) + Zy(1,1,1) ( y - 1)
(το z το έγραψα με κεφαλαίο για να ξεχωρίζει η μερική παράγωγος ως προς x και ως προς y)
και η κάθετη θα δίνεται από τον τύπο για συναρτήσεις της μορφής z = z(x,y):
x-1 / Zx(1,1,1) = y - 1 / Zy(1,1,1) = z - 1 / -1
τι λέτε;
αν στη F θέσεις όπου x = y = 1 δηλαδή το σημείο (1,1) θα σου βγει z^3 + z - 2 = 0 και στο τέλος λέει ώστε z(1,1) = 1 ή z = 1 το οποίο επαληθεύεται.
το ότι ορίζει σε πεπλεγμένη μορφή συνάρτηση z = z(x,y) το αποδεικνύεται από τους τύπους:
Zx = - Fx / Fz και Zy = - Fy / Fz τα οποία στο σημείο (1,1) πρέπει να βγουν διάφορα του μηδενός για το σημείο (1,1,1)
και μετά για το
γ) το εφαπτόμενο δίνεται από τον τύπο: Z - 1 = Zx(1,1,1) ( x - 1) + Zy(1,1,1) ( y - 1)
(το z το έγραψα με κεφαλαίο για να ξεχωρίζει η μερική παράγωγος ως προς x και ως προς y)
και η κάθετη θα δίνεται από τον τύπο για συναρτήσεις της μορφής z = z(x,y):
x-1 / Zx(1,1,1) = y - 1 / Zy(1,1,1) = z - 1 / -1
τι λέτε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 17:40:57 pm
ναι λογικα ετσι βγαινει !
απλα δεν ηξερα πως δειχνεις οτι ειναι πεπλεγμενη και για το z μετα τι τιμη βαζεις...
για το 3ο καμια ιδεα ?
απλα δεν ηξερα πως δειχνεις οτι ειναι πεπλεγμενη και για το z μετα τι τιμη βαζεις...
για το 3ο καμια ιδεα ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airpap on September 14, 2014, 18:06:58 pm
για το 4ο επισης? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 19:00:15 pm
στις λυσεις που υπαρχουν στα downloads στα θεματα του ατρεα Ιουνιος 2014 θεμα 2α εχω την εντυπωση οτι τα ορια για το y πρεπει να ειναι -1>0 και 0->1 και οχι -2>0 και 0->2
Επίσης το θεμα 1β σας βγαινει??
Επίσης το θεμα 1β σας βγαινει??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 14, 2014, 19:22:30 pm
λογικά ναι, αφού τα y είναι από το 0-1.
να προτείνω έναν άλλο τρόπο να μου πείτε αν είναι σωστός? κάνοντας το σχήμα πήρα το τρίγωνο που σχηματίζεται στο 1 τεταρτημόριο και έλυσα το διπλό ολοκλήρωμα. αυτό που βρήκα το πολλαπλασίασα με το 4 (γιατί έχω τέσσερα ίδια τρίγωνα). Ισχύει?
για το 1β, ναι μου βγήκε μετά από πολύ κόπο και προσπάθεια. θα το καθαρογράψω να στο στείλω αν θες.
παίζει να ελυσε κανείς τα θέματα 4-5 του ατρέα?
να προτείνω έναν άλλο τρόπο να μου πείτε αν είναι σωστός? κάνοντας το σχήμα πήρα το τρίγωνο που σχηματίζεται στο 1 τεταρτημόριο και έλυσα το διπλό ολοκλήρωμα. αυτό που βρήκα το πολλαπλασίασα με το 4 (γιατί έχω τέσσερα ίδια τρίγωνα). Ισχύει?
για το 1β, ναι μου βγήκε μετά από πολύ κόπο και προσπάθεια. θα το καθαρογράψω να στο στείλω αν θες.
παίζει να ελυσε κανείς τα θέματα 4-5 του ατρέα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 14, 2014, 19:27:11 pm
για το 4ο) ΣΕΠ2013:
- για το α), για να είναι ανεξάρτητο δεν θα πρέπει να ισχύει:
dR/dy = dQ/dz και dP/dz = dR/dx και dQ/dx = dP/dy???
άρα ... f = xy
- και για το β) το δυναμικό δεν βγαίνει από το τύπο με τα ολοκληρώματα;
ολοκλήρωμα από 0 έως x P(x,y,z)dx + ολοκλήρωμα από 0 έως y Q(0,y,z)dy + ολοκλήρωμα από 0 έως z R(0,0,z)dz + c και μετά βρίσκεις και την σταθερά c από το σημείο που σου δίνει ως δεδομένο
τι λέτε;
- για το α), για να είναι ανεξάρτητο δεν θα πρέπει να ισχύει:
dR/dy = dQ/dz και dP/dz = dR/dx και dQ/dx = dP/dy???
άρα ... f = xy
- και για το β) το δυναμικό δεν βγαίνει από το τύπο με τα ολοκληρώματα;
ολοκλήρωμα από 0 έως x P(x,y,z)dx + ολοκλήρωμα από 0 έως y Q(0,y,z)dy + ολοκλήρωμα από 0 έως z R(0,0,z)dz + c και μετά βρίσκεις και την σταθερά c από το σημείο που σου δίνει ως δεδομένο
τι λέτε;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 19:27:22 pm
Quote
να προτείνω έναν άλλο τρόπο να μου πείτε αν είναι σωστός? κάνοντας το σχήμα πήρα το τρίγωνο που σχηματίζεται στο 1 τεταρτημόριο και έλυσα το διπλό ολοκλήρωμα. αυτό που βρήκα το πολλαπλασίασα με το 4 (γιατί έχω τέσσερα ίδια τρίγωνα). Ισχύει?
σωστο μου φαινεταιQuote
για το 1β, ναι μου βγήκε μετά από πολύ κόπο και προσπάθεια. θα το καθαρογράψω να στο στείλω αν θες.
ναι αν μπορεις στειλε λιγο γιατι εχω κολλησει. μου βγαινουν ολα εκτος απο την fxTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 14, 2014, 19:31:57 pm
ΣΕΠ2013 Θέμα 3ο έχει να κάνει με ακρότατα και πολ/στες Lagrange ή όχι;
γιατί αν είναι έτσι, θέτεις την επιφάνεια της σφαίρας ως g(x,y,z) = x^2 + y^2 + z^2 - 1
και T(x,y,z) = x - 2y + 2z άρα ψάχνεις για τα ακρότατα της f(x,y,z) = T(x,y,z) + λ g(x,y,z) και έπειτα τα γνωστά;
δλδ να θεωρήσεις ότι ψάχνεις την μέγιστη-ελάχιστη θερμοκρασία που δίνεται από την Τ(x,y,z) υπό τον περιορισμό της g(x,y,z)
γιατί αν είναι έτσι, θέτεις την επιφάνεια της σφαίρας ως g(x,y,z) = x^2 + y^2 + z^2 - 1
και T(x,y,z) = x - 2y + 2z άρα ψάχνεις για τα ακρότατα της f(x,y,z) = T(x,y,z) + λ g(x,y,z) και έπειτα τα γνωστά;
δλδ να θεωρήσεις ότι ψάχνεις την μέγιστη-ελάχιστη θερμοκρασία που δίνεται από την Τ(x,y,z) υπό τον περιορισμό της g(x,y,z)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 19:34:59 pm
δεν μπορεις να λυσεις ως προς x στον τυπο της σφαιρας και να το βαλεις στην Τ και μετα να βρεις ακροτατα ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 14, 2014, 19:42:26 pm
το 1β αναλυτικά
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 14, 2014, 19:47:31 pm
δν ξέρω, με lagrange θα το έκανα. από την στιγμή που σου δίνονται δυο συναρτήσεις, θερμοκρασίας και σφαίρα στην ουσία, θέτεις περιορισμό και προχωράς... δν ξέρω αν βγαίνει το ίδιο ή αν αυτό που λέω εγώ είναι σωστό :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 14, 2014, 19:50:56 pm
για το θεμα 7 φεβρουαριος 14 καμια βοηθεια ? ειναι ανοικτη ή κλειστη η καμπυλη ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 14, 2014, 20:01:02 pm
δν ξέρω, με lagrange θα το έκανα. από την στιγμή που σου δίνονται δυο συναρτήσεις, θερμοκρασίας και σφαίρα στην ουσία, θέτεις περιορισμό και προχωράς... δν ξέρω αν βγαίνει το ίδιο ή αν αυτό που λέω εγώ είναι σωστό :)
ναι εχεις δικιο τωρα π το ξαναβλεπω με lagrange καλυτερα ! τνξ !
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 14, 2014, 21:25:18 pm
Φεβρουαριος 14 θεμα 8 μπορει να βοηθησει καποιος ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 21:52:59 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 14, 2014, 22:13:55 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
ελα παιδια καποιος ....μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: alexpaxi on September 14, 2014, 22:19:00 pm
στο 4ο θεμα του ιουνιου του 2014 στο Ξενο Β ομαδα στο β ερωτημα εχει λαθος στο διανυσματικο πεδιο G?γιατι δεν μου βγαινει divG=0 για να πω οτι προερχεται απο διανυσματικο δυναμικο.
μαλλον καπου εχεις λαθος, γιατι 0 βγαινει... κανω divG=dP/dx + dQ/dy + dR/dz αλλα αυτο ειναι διαφορο του 0.η F=(2x+4yz,2y,4xy-z)
και G=F + (0,4xz,0) δηλαδη G=(2x+4yz,2y+4xz,4xy-2z) ετσι δεν ειναι?δν προσθετω τα 2 πεδια και βγαζω ενα ενιαιο για το οποιο κανω DivG=.... ???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 22:25:58 pm
στο 4ο θεμα του ιουνιου του 2014 στο Ξενο Β ομαδα στο β ερωτημα εχει λαθος στο διανυσματικο πεδιο G?γιατι δεν μου βγαινει divG=0 για να πω οτι προερχεται απο διανυσματικο δυναμικο.
μαλλον καπου εχεις λαθος, γιατι 0 βγαινει... κανω divG=dP/dx + dQ/dy + dR/dz αλλα αυτο ειναι διαφορο του 0.η F=(2x+4yz,2y,4xy-z)
και G=F + (0,4xz,0) δηλαδη G=(2x+4yz,2y+4xz,4xy-2z) ετσι δεν ειναι?δν προσθετω τα 2 πεδια και βγαζω ενα ενιαιο για το οποιο κανω DivG=.... ???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 14, 2014, 22:31:56 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
το 4α πως το κανες? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ALEO on September 14, 2014, 22:32:16 pm
Ιουνιος 2013 θεμα 2γ τμημα κ. Ξενου. Ξερει κανεις πως υπολογιζεται το εργο?? Ξερω οτι ειναι το ολοκληρωμα του F*dr/dt dt αλλα πως βρισκουμε το r(t)???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: alexpaxi on September 14, 2014, 22:33:34 pm
στο 4ο θεμα του ιουνιου του 2014 στο Ξενο Β ομαδα στο β ερωτημα εχει λαθος στο διανυσματικο πεδιο G?γιατι δεν μου βγαινει divG=0 για να πω οτι προερχεται απο διανυσματικο δυναμικο.
μαλλον καπου εχεις λαθος, γιατι 0 βγαινει... κανω divG=dP/dx + dQ/dy + dR/dz αλλα αυτο ειναι διαφορο του 0.η F=(2x+4yz,2y,4xy-z)
και G=F + (0,4xz,0) δηλαδη G=(2x+4yz,2y+4xz,4xy-2z) ετσι δεν ειναι?δν προσθετω τα 2 πεδια και βγαζω ενα ενιαιο για το οποιο κανω DivG=.... ???
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 22:37:44 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
το 4α πως το κανες? :-\
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 22:42:03 pm
το 4α πως το κανες? :-\
Eιδικότερα, αν ο τόπος D είναι απλά συνεκτικός, τότε ισχύει:
To F είναι συντηρητικό επί απλά συνεκτικού τόπου D αν και
µόνον αν το πεδίο F έχει συνεχείς µερικές παραγώγους και είναι
αστρόβιλο επί του D.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 22:44:08 pm
το 4α πως το κανες? :-\
Για να είναι συντηρητικό το F στον R3 θα πρέπει να είναι αστρόβιλο. Αμα πάρεις rotF βγαίνει (z - x, 0, z - x) != 0 οπότε δεν είναι συντηρητικό. Αυτό ισχύει μόνο και μόνο επείδη ο R3 είναι απλά συνεκτικός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 22:45:41 pm
το 4α πως το κανες? :-\
Για να είναι συντηρητικό το F στον R3 θα πρέπει να είναι αστρόβιλο. Αμα πάρεις rotF βγαίνει (z - x, 0, z - x) != 0 οπότε δεν είναι συντηρητικό. Αυτό ισχύει μόνο και μόνο επείδη ο R3 είναι απλά συνεκτικός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 14, 2014, 22:46:14 pm
το ανω ημισφαιριο της ελλειψης ειναι ανοικτη ή κλειστη καμπυλη ?? (μηπως επειδη φραζεται απο τον αξωνα των χ ειναι κλειστη ?(επεσε θεμα 7 Φεβρ 2014))
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 22:50:06 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
Άμα βάλεις t=1 και t=3 στην r(t) προκύπτουν τα Α και Β. Το γεγονός ότι δίνει και τα σημεία και το που ανήκει το z είναι πλεονασμός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 22:51:05 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
Άμα βάλεις t=1 και t=3 στην r(t) προκύπτουν τα Α και Β. Το γεγονός ότι δίνει και τα σημεία και το που ανήκει το z είναι πλεονασμός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: creat.ure on September 14, 2014, 22:52:58 pm
Ατρέας Ιούνης 2014 θέμα 4β ->
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
Ξένος 2014 θέμα,5ο βγαίνει ροή = 2V, και V = 2*16*sqrt(2)*2pi/3 ?? ή αλλιώς = 94.78???????
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
Ξένος 2014 θέμα,5ο βγαίνει ροή = 2V, και V = 2*16*sqrt(2)*2pi/3 ?? ή αλλιώς = 94.78???????
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: night.atk on September 14, 2014, 22:53:10 pm
Ιουνιος 2013 θεμα 2γ τμημα κ. Ξενου. Ξερει κανεις πως υπολογιζεται το εργο?? Ξερω οτι ειναι το ολοκληρωμα του F*dr/dt dt αλλα πως βρισκουμε το r(t)???
Αφου εχεις συντηρητικο πεδίο το έργο δεν εξαρτάται απο την καμπύλη που ενώνει τα σημεία Α και Β αλλά μόνο απο το αρχικο και το τελικό σημείο,δηλαδή ολοκληρωμα F*dr για ΑΒ = F(A)-F(B)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 22:59:50 pm
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
Άμα βάλεις t=1 και t=3 στην r(t) προκύπτουν τα Α και Β. Το γεγονός ότι δίνει και τα σημεία και το που ανήκει το z είναι πλεονασμός.
Έτσι νομίζω αλλά με προβληματίζει το γεγονός ότι καταλήγει σε αυτό: http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3 (http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 14, 2014, 23:02:30 pm
Έτσι νομίζω αλλά με προβληματίζει το γεγονός ότι καταλήγει σε αυτό: http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3 (http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3)
Ατρέας Ιούνης 2014 θέμα 4β ->
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 23:08:06 pm
Έτσι νομίζω αλλά με προβληματίζει το γεγονός ότι καταλήγει σε αυτό: http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3 (http://www.wolframalpha.com/input/?i=integrate+4t^9%2B2t^6%2Bt^3+dt%2C+t%3D1..3)
Ατρέας Ιούνης 2014 θέμα 4β ->
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
y=t , z=sqrt(t), x=t^2 ,και όρια ολοκλήρωσης από τ=1 μέχρι τ=9.
Βγαίνει 23736 τ αποτέλεσμα, επαληθεύστε,
Είναι αρκετά κοντά τα νούμερα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 14, 2014, 23:22:24 pm
Φεβρουαριος 14 θεμα 8 μπορει να βοηθησει καποιος ?
εμενα μου βγηκε με θεωρημα gauss και συγκεκριμενα εβγαλα το ολοκληρωμα 25/4. Αν το εκανε κανεις αλλος για επιβεβαιωση...
Επισης στο ερώτημα 7 των ίδιων εξετάσεων μου βγήκε το ολοκλήρωμα 8/3. Επίσης κι αυτό κανείς να το επιβεβαιώσει...
Τέλος, υπάρχει καμιά ιδέα για το ερώτημα 5?? Έχω σκαλώσει εκεί.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 23:32:21 pm
Επισης στο ερώτημα 7 των ίδιων εξετάσεων μου βγήκε το ολοκλήρωμα 8/3. Επίσης κι αυτό κανείς να το επιβεβαιώσει...
Εγώ το βγαλά 64/3 αλλά παίζει να έκανα αριθμητικό. Πως το κάνες;
Edit: Είχα όντως αριθμητικό και έβγαλα και γω 8/3
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: creat.ure on September 14, 2014, 23:35:51 pm
Ξένος 2014 θέμα,5ο βγαίνει ροή = 2V, και V = 64.145
ξαναπόσταρα, γιατί άλλαξε η τιμή κ μήπως το δει κανείς
ξαναπόσταρα, γιατί άλλαξε η τιμή κ μήπως το δει κανείς
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 14, 2014, 23:40:01 pm
Επισης στο ερώτημα 7 των ίδιων εξετάσεων μου βγήκε το ολοκλήρωμα 8/3. Επίσης κι αυτό κανείς να το επιβεβαιώσει...
Εγώ το βγαλά 64/3 αλλά παίζει να έκανα αριθμητικό. Πως το κάνες;
με θεώρημα stokes πήγα απτο επικαμπύλιο στο επιφανειακό και μετά έλυσα το επιφανειακό πάνω στη μισή έλλειψη. Έβαλα μετά πολικές συντεταγμένες. Τώρα που το ξαναβλέπω έκανα κι εγώ ένα λάθος στις πράξεις. Βγαίνει τώρα (8* ριζα2 )/3. Είχα ξεχάσει τον συντελεστή απτην αλλαγή συντεταγμένων.
Ο τρόπος σωστός δεν είναι? Ενταξει λάθη αριθμητικα μπορεί να εχουμε κανει και οι 2.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 14, 2014, 23:44:13 pm
Επισης στο ερώτημα 7 των ίδιων εξετάσεων μου βγήκε το ολοκλήρωμα 8/3. Επίσης κι αυτό κανείς να το επιβεβαιώσει...
Εγώ το βγαλά 64/3 αλλά παίζει να έκανα αριθμητικό. Πως το κάνες;
με θεώρημα stokes πήγα απτο επικαμπύλιο στο επιφανειακό και μετά έλυσα το επιφανειακό πάνω στη μισή έλλειψη. Έβαλα μετά πολικές συντεταγμένες. Τώρα που το ξαναβλέπω έκανα κι εγώ ένα λάθος στις πράξεις. Βγαίνει τώρα (8* ριζα2 )/3. Είχα ξεχάσει τον συντελεστή απτην αλλαγή συντεταγμένων.
Ο τρόπος σωστός δεν είναι? Ενταξει λάθη αριθμητικα μπορεί να εχουμε κανει και οι 2.
Α έχεις δίκιο και γω ξέχασα τον τελεστή τώρα :P
Πάντως εγώ το πήγα με green απευθείας
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geomade on September 14, 2014, 23:46:12 pm
Επισης στο ερώτημα 7 των ίδιων εξετάσεων μου βγήκε το ολοκλήρωμα 8/3. Επίσης κι αυτό κανείς να το επιβεβαιώσει...
Εγώ το βγαλά 64/3 αλλά παίζει να έκανα αριθμητικό. Πως το κάνες;
με θεώρημα stokes πήγα απτο επικαμπύλιο στο επιφανειακό και μετά έλυσα το επιφανειακό πάνω στη μισή έλλειψη. Έβαλα μετά πολικές συντεταγμένες. Τώρα που το ξαναβλέπω έκανα κι εγώ ένα λάθος στις πράξεις. Βγαίνει τώρα (8* ριζα2 )/3. Είχα ξεχάσει τον συντελεστή απτην αλλαγή συντεταγμένων.
Ο τρόπος σωστός δεν είναι? Ενταξει λάθη αριθμητικα μπορεί να εχουμε κανει και οι 2.
Α έχεις δίκιο και γω ξέχασα τον τελεστή τώρα :P
Πάντως εγώ το πήγα με green
ναι οκ το ιδιο καναμε βασικα. green χρησιμοποιησα κι εγω ουσιαστικα αφου ειναι στο x,y :P
Τέλος, υπάρχει καμιά ιδέα για το ερώτημα 5?? Έχω σκαλώσει εκεί.....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: svart on September 15, 2014, 00:02:01 am
Τέλος, υπάρχει καμιά ιδέα για το ερώτημα 5?? Έχω σκαλώσει εκεί.....
Χωρίς να είμαι απολύτως σίγουρος, αμά πάρεις την κλίση του εφαπτόμενου διανύσματος, δλδ τη παράγωγο της r θα είναι (-Αsint, Acost, B) δλδ dr/dz=Β άρα ανεξάρτητο του t
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 15, 2014, 01:55:37 am
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
το F πως το βγάζουμε ρε γαμώτι?!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DarkPassenger on September 15, 2014, 02:02:46 am
θεματα Ατρεα Ιουνιος 2014 πως παραμετροποιούμε στο 4β ??
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
μήπως
z=t
y=t^2
x=t^4 , 1<t<3
οπότε r(t) = (t^4, t^2, t),
F = (t^6,t^5,t^3)
και παιρνουμε το ολοκληρωμα(F(t)* r'(t)) απο 1 ως 3? αλλά το Α και Β που το χρησιμοποιούμε? :/
το F πως το βγάζουμε ρε γαμώτι?!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 15, 2014, 02:08:53 am
ιιιι, στα διάλα, δεν είχα δει οτι ήταν ίδια και για το β ερώτημα -.-
ευχαριστώ πολυυυυυυυ!
ευχαριστώ πολυυυυυυυ!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kwstas123 on September 16, 2014, 00:56:50 am
Μπορει κανεις να ανεβασει τα σημερινα τα θεματα του Ατρεα???? :) :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 16, 2014, 01:05:50 am
Μπορει κανεις να ανεβασει τα σημερινα τα θεματα του Ατρεα???? :) :)
δεν είχα κάμερα να τα βγάλω, αν δεν τα χει πάρει κανείς, πες μου να σου πω τι έπεσε γενικά σαν θέματα!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kwstas123 on September 16, 2014, 01:18:32 am
Μπορει κανεις να ανεβασει τα σημερινα τα θεματα του Ατρεα???? :) :)
δεν είχα κάμερα να τα βγάλω, αν δεν τα χει πάρει κανείς, πες μου να σου πω τι έπεσε γενικά σαν θέματα!
Για πες...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: unique on September 16, 2014, 01:29:53 am
Θέμα 4 του Ιουνίου 14
να βρεις το ελάχιστο μιας συνάντησης υπό συνθήκη
διπλό ολοκλήρωμα που να αντιστρεψεις τα dx, dy και να το λύσεις
επιφανειακό ολοκλήρωμα
απόδειξη με gauss
Εξίσωση παραλλήλου επιπέδου και κάθετης
Πλεγμενη συνάρτηση να πεις αν λύνεται ως προς y και να αιτιολογησεις
Σου δινε τη λαπλασιανη (αναδελτα^2 F=0 ) και ήθελε να αποδείξεις οτι το πεδίο ειναι ασυμπιεστο
Κάτι με green έλυσα επίσης.
Αν θυμηθώ τίποτα άλλο θα το συμπληρώσω...
να βρεις το ελάχιστο μιας συνάντησης υπό συνθήκη
διπλό ολοκλήρωμα που να αντιστρεψεις τα dx, dy και να το λύσεις
επιφανειακό ολοκλήρωμα
απόδειξη με gauss
Εξίσωση παραλλήλου επιπέδου και κάθετης
Πλεγμενη συνάρτηση να πεις αν λύνεται ως προς y και να αιτιολογησεις
Σου δινε τη λαπλασιανη (αναδελτα^2 F=0 ) και ήθελε να αποδείξεις οτι το πεδίο ειναι ασυμπιεστο
Κάτι με green έλυσα επίσης.
Αν θυμηθώ τίποτα άλλο θα το συμπληρώσω...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pocitician on September 16, 2014, 11:22:50 am
ΞΕΝΟΣ
- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: riko5 on September 16, 2014, 15:03:34 pm
ΞΕΝΟΣ
- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
Τα ανεβασα πριν απο λιγο πρεπει να εγκριθουν πρωτα και μετα θα υπαρχουν και στα downloads...- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: pentium4 on September 16, 2014, 15:35:00 pm
ΞΕΝΟΣ
- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
Τα ανεβασα πριν απο λιγο πρεπει να εγκριθουν πρωτα και μετα θα υπαρχουν και στα downloads...- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
έγινε και αυτό..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: kwstas123 on September 17, 2014, 18:19:54 pm
ΞΕΝΟΣ
- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
Τα ανεβασα πριν απο λιγο πρεπει να εγκριθουν πρωτα και μετα θα υπαρχουν και στα downloads...- παράγωγος κατά κατεύθυνση, ακρότατα, ισοσταθμική, εφαπτόμενο επίπεδο
- απόδειξη ότι το πεδίο είναι συντηρητικό, να βρεθεί έργο μεταξύ δυο σημείων Α και Β, να βρεθεί δυναμικό σε ένα σημείο
- να βρεθεί εμβαδόν και μήκος μεταξύ δυο καμπυλών
- να βρεθεί ροή διανυσματικού πεδίου και εμβαδόν μιας κυλινδρικής επιφάνειας
^wav^
ααν βρει κανεις και του ατρεα, ας τα ανεβασει :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 17, 2015, 15:48:47 pm
Θέματα Ιανουαρίου 2015 Ατρέας υπάρχουν ? 'Οποιος τα έχει ας κάνει ένα κόπο να τα ανεβάσει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on August 25, 2015, 17:58:42 pm
Μπορεί να μου εξηγήσει κάποιος στη 2η ΠΡΟΟΔΟ 2014 θεμα 2/α πως γίνεται η παραμετροποίηση?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: emmae on September 02, 2015, 20:25:42 pm
ανεβαστε οτι λυμενο εχετε!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on September 05, 2015, 15:35:07 pm
Μπορει καποιος να ανεβασει σημειωσεις απο Ζαχαρη;
Ακουγεται οτι βαζει απο εκει.
Thanks
Ακουγεται οτι βαζει απο εκει.
Thanks
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 11, 2015, 13:30:22 pm
ειδε κανεις θεμα 3 ιουνη '15 ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 11, 2015, 20:21:13 pm
Εχει κανα καλο παιδι αποτελεσματα απο θεμα 1,ιουνιος '15;
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 11, 2015, 20:40:03 pm
Εχει κανα καλο παιδι αποτελεσματα απο θεμα 1,ιουνιος '15;
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
για το πρωτο ερωτημα μπορω να πω z * (z^2+1) = 10 - 4x - 2y -- > f(x,y)* [f(x,y)^2 + 1] = 10 - 4x - 2y και για x=0, y=0 f(0,0)=2 αρα ισχυει η σχεση ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 11, 2015, 20:44:41 pm
Εχει κανα καλο παιδι αποτελεσματα απο θεμα 1,ιουνιος '15;
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
(βασικα και ολα να τα ανεβασει αυτο το καλο παιδι, θα ειναι gg)
για το πρωτο ερωτημα μπορω να πω z * (z^2+1) = 10 - 4x - 2y -- > f(x,y)* [f(x,y)^2 + 1] = 10 - 4x - 2y και για x=0, y=0 f(0,0)=2 αρα ισχυει η σχεση ?
Και τα αλλα απο ενα θεωρημα που ειχε στο κεφ3 των σημειωσεων,απλως αμα τα λυσεις ποσταρε για cross check :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 11, 2015, 21:10:39 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 11, 2015, 21:34:35 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
^peace^ στα παντα. για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 11, 2015, 22:06:26 pm
για το (β) η διευθυνση της εφαπτομενης ευθειας της καμπυλης που λεει ειναι το grad g(0,0) αν ονομασουμε g την καμπυλη που δινει..?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 11, 2015, 22:28:39 pm
Ναι, στην ουσια αυτο θα ειναι το διανυσμα α, κατα του οποιου θα παρεις τη διευθυνση..
Δηλαδη στον τυπο θf/θα=gradf*a/||a|| οπου a θα βαλεις το (θg/θx,θg/θy)
Δηλαδη στον τυπο θf/θα=gradf*a/||a|| οπου a θα βαλεις το (θg/θx,θg/θy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 11, 2015, 22:40:02 pm
ωραιος τνξ..! βρηκα βσκ την κλιση της z στο (0,0) ιση με (-4/13 , -2/13) και το α0 ισο με (0,-1) αρα τελικα το ζητομενο προκυπτει ως (-4/13,-2/13) * (0.-1) = 2/13 .. ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 11, 2015, 23:58:05 pm
ωραιος τνξ..! βρηκα βσκ την κλιση της z στο (0,0) ιση με (-4/13 , -2/13) και το α0 ισο με (0,-1) αρα τελικα το ζητομενο προκυπτει ως (-4/13,-2/13) * (0.-1) = 2/13 .. ??
Κουλ.ειδε κανεις θεμα 3 ιουνη '15 ?
Hang tight to your seat, here it comesΕπειδη το χωριο ετσι οπως στο δινει ειναι τμημα σφαιρας, παιρνεις σφαιρικες συντεταγμενες:
x=rcosθsinφ / y=rsinθsinφ / z=rcosφ / dxdydz=r2sinφdrdθdφ
αντικαθιστωντας βγαινει 2<=r<=3
αρα το ολοκληρωμα ειναι r απο 2 εως 3, θ απο 0 εως π και φ απο 0 εως π/2 γιατι πρεπει να παρεις το μερος που ειναι x,z>=0
μεσα απο την αντικατασταση βγαινει r3sinφdrdθdφ
Αποτελεσμα βγαζω 16,25 που μου φαινεται ακυρο σα νουμερο
Υ.Γ. Αν αλλαξω τα ορια στο θ,φ βγαινει ενα ωραιοτατο 65π αλλα δεν ειμαι σιγουρος πως να διαλεξω.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 00:04:23 am
στο 2ο θεμα οι εξισωσεις ειναι το εσωτερικο γινομενο των gradΦ1( 5,1,-1) και gradΦ2(5,1,-1) να ειναι ισο με μηδεν και Φ2(5,1,-1)=0 ?
3ο θεμα σωστο οπως το λες απλα εχω την εντυπωση πως το θ παει απο 0 εως 2π επειδη η προβολη του στερεου στον Oxy ειναι δακτυλιος και θες να τον καλυψεις ολο .. η μηπως θα πρεπε να ναι -π/2 εως π/2 γιατι x>=0 ? αν το δεις σαν κυκλο τα θετικα χ ειναι σ αυτο το διαστημα.. δν ξερω..
3ο θεμα σωστο οπως το λες απλα εχω την εντυπωση πως το θ παει απο 0 εως 2π επειδη η προβολη του στερεου στον Oxy ειναι δακτυλιος και θες να τον καλυψεις ολο .. η μηπως θα πρεπε να ναι -π/2 εως π/2 γιατι x>=0 ? αν το δεις σαν κυκλο τα θετικα χ ειναι σ αυτο το διαστημα.. δν ξερω..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 00:10:45 am
3ο θεμα σωστο οπως το λες απλα εχω την εντυπωση πως το θ παει απο 0 εως 2π επειδη η προβολη του στερεου στον Oxy ειναι δακτυλιος και θες να τον καλυψεις ολο .. η μηπως θα πρεπε να ναι -π/2 εως π/2 γιατι x>=0 ? αν το δεις σαν κυκλο τα θετικα χ ειναι σ αυτο το διαστημα.. δν ξερω..
Κοιτα σιγουρα εχω καποιο λαθος με τα ορια ολοκληρωσεις,αν το βρεις στειλε γιατι τα νουμερα που βρηκα ειναι ανωμαλα.εδιτ: αν παρω φ απο -π/2 εως π/2 βγαινει ολο το ολοκληρωμα 0 παντως.
στο 2ο θεμα οι εξισωσεις ειναι το εσωτερικο γινομενο των gradΦ1( 5,1,-1) και gradΦ2(5,1,-1) να ειναι ισο με μηδεν και Φ2(5,1,-1)=0 ?
Νομιζω ναι, βγαινει b=2 και a=βαρεθηκα να το βγαλω ;DTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 00:33:28 am
οχι το φ, αυτο παει απο 0 εως π/2.... το θ ειναι αυτο που δεν ξερω αν ειναι [0, 2π], [0,π] ή [-π/2,π/2] γιατι σ λεει οτι πρεπει και x >= 0 .. δν τα βγαλα τα νουμερα :P
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 12:06:21 pm
για το θεμα 4 (β) με το βαθμωτο δινει f(0,0,0)=3 αρα στο επικαμπυλιο ολοκληρωμα F(r(t)) * r'(t) dt θα παρουμε απο το 3 η απο το 0 για το κατω οριο ? και το r(t) ποιο θα ειναι ? το (tx,ty,tz) , t=[0,1] ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zumo naranja on September 12, 2015, 15:38:29 pm
2015, θεμα 5α, πως σκατα βγαζουμε το εμβαδον? Εχω ζαλιστει!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 15:54:54 pm
οχι το φ, αυτο παει απο 0 εως π/2.... το θ ειναι αυτο που δεν ξερω αν ειναι [0, 2π], [0,π] ή [-π/2,π/2] γιατι σ λεει οτι πρεπει και x >= 0 .. δν τα βγαλα τα νουμερα :P
Το παιδεψα χτες βραδυ και δεν εβγαλα χριστο, εχω αρχισει να εκνευριζομαι με το θεμα (εδινε και 1μιση μοναδα γαμω)2015, θεμα 5α, πως σκατα βγαζουμε το εμβαδον? Εχω ζαλιστει!
no idea,bruhTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zumo naranja on September 12, 2015, 16:02:48 pm
οχι το φ, αυτο παει απο 0 εως π/2.... το θ ειναι αυτο που δεν ξερω αν ειναι [0, 2π], [0,π] ή [-π/2,π/2] γιατι σ λεει οτι πρεπει και x >= 0 .. δν τα βγαλα τα νουμερα :P
Το παιδεψα χτες βραδυ και δεν εβγαλα χριστο, εχω αρχισει να εκνευριζομαι με το θεμα (εδινε και 1μιση μοναδα γαμω)2015, θεμα 5α, πως σκατα βγαζουμε το εμβαδον? Εχω ζαλιστει!
no idea,bruhγια το πανω εγω νομιζω οτι παει απο -π/2 εως π/2.
για το εμβαδον που ρωτησα, νομιζω οτι ολοκληρωνεις ως προς z (7 εως 12) και φ (0 εως 2π) και ως ολοκληρωτεα ποσοτητα αντικαθιστας το ds=ρdzdφ και οπου ρ βαζω ριζα 16-z.
το αποτελεσμα βγαινει περιπου οσο το βγαζει και ο cone calculator που χρησιμοποιησα για να το επιβεβαιωσω, δηλαδη περιπου 80
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 12, 2015, 16:30:54 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
μάλλον άκυρο τελικά, αντί για την Φ πηρα την f στον τυπο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 16:41:27 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
στο γ γιατι (4,2,13)? δεν θα έπρεπε να είναι (-4/13,-2/13,2(?)) για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
για το πανω εγω νομιζω οτι παει απο -π/2 εως π/2.
δε νομιζω η φ να ειναι εκει γιατι μεσα στο ολοκληρωμα εχεις sinφ που θα γινει -cosφ και θα μηδενιστει οποτε θα βγει 0 ολοκληροTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 12, 2015, 16:47:21 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
στο γ γιατι (4,2,13)? δεν θα έπρεπε να είναι (-4/13,-2/13,2(?)) για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
μάλλον δικό μου ήταν το λάθος τελικά
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 16:50:14 pm
αα ναι σωστος δικιο εχεις !
για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
στο γ γιατι (4,2,13)? δεν θα έπρεπε να είναι (-4/13,-2/13,2(?)) για το (γ) ειναι r(t) = (0,0,2) + λ ( 4,2,13) ? ( τυπος σελ 81 )
το (β) δν το δα ακομα..
μάλλον δικό μου ήταν το λάθος τελικά
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 12, 2015, 17:02:49 pm
Τα Φχ και Φy ειναι 4 και 2, εγώ απο λάθος πηρα τα fx kαι fy που ειναι -4/13 και -2/13 γι'αυτο ειπα (-4/13,-2/13,2) αλλά ο αρχικός είχε δίκιο και ειναι (4,2,13)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 17:04:36 pm
ναι εγω πηρα την Φ = z^3 + z + 4x + 2y - 10....αρα grad Φ (Po) ψαχνω και grad Φ = (4,2,3z^2+1) ..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 18:06:58 pm
ναι εγω πηρα την Φ = z^3 + z + 4x + 2y - 10....αρα grad Φ (Po) ψαχνω και grad Φ = (4,2,3z^2+1) ..
kewl, τωρα το ειδα το λαθος μουTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 18:09:53 pm
παιζει να δες και θεμα 2(γ) απο ιουνη '14 ? :D
γενικα καποια στιγμη νομιζω αντικαθιστας με πολικες συντεταγμενες το τριπλο ολοκληρωμα ?? αυτες θα ναι οι x = a * ρ * cos θ
και y = b * ρ * sinθ ? οπου ρ ανηκει στο [0,1] ?
γενικα καποια στιγμη νομιζω αντικαθιστας με πολικες συντεταγμενες το τριπλο ολοκληρωμα ?? αυτες θα ναι οι x = a * ρ * cos θ
και y = b * ρ * sinθ ? οπου ρ ανηκει στο [0,1] ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 12, 2015, 18:26:10 pm
παιζει να δες και θεμα 2(γ) απο ιουνη '14 ? :D
γενικα καποια στιγμη νομιζω αντικαθιστας με πολικες συντεταγμενες το τριπλο ολοκληρωμα ?? αυτες θα ναι οι x = a * ρ * cos θ
και y = b * ρ * sinθ ? οπου ρ ανηκει στο [0,1] ?
γενικα καποια στιγμη νομιζω αντικαθιστας με πολικες συντεταγμενες το τριπλο ολοκληρωμα ?? αυτες θα ναι οι x = a * ρ * cos θ
και y = b * ρ * sinθ ? οπου ρ ανηκει στο [0,1] ?
Yep έτσι βγαίνει
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 12, 2015, 18:28:16 pm
tnx !!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: gioti488 on September 12, 2015, 19:56:27 pm
Στα θέματα του Ιουνίου 2015, Θέμα 5α, πώς παίρνω τα όρια για τη θ? Από -π/2 έως π/2 ή από 0 έως 2π? Γενικά τι παίζει,πως καταλαβαίνω τα όρια για θ και φ,γνωρίζει κάποιος?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 12, 2015, 22:27:59 pm
Στα θέματα του Ιουνίου 2015, Θέμα 5α, πώς παίρνω τα όρια για τη θ? Από -π/2 έως π/2 ή από 0 έως 2π? Γενικά τι παίζει,πως καταλαβαίνω τα όρια για θ και φ,γνωρίζει κάποιος?
Γενικα παιζει θεμα με τις σφαιρικες, αλλα ειδα σε ενα βιβλιο του τσιμπουκη για ασκησεις πεδιο 1, οτι η γωνια φ μετριεται απο τον αξονα z με τη φορα του ρολογιου και η θ απο τον x με ανθωρολογιακη φορα.Οποτε go figure.Δεν εχω ιδεα βεβαια αν ειναι ετσι οντως
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2015, 11:02:32 am
στο θεμα 2(α) του ιουνη του '14 τι ορια πηρατε ?? το σπασα σε αθροισμα 2 ολοκληρωματων το ενα με ορια [0,1]για y και για x [-2+2y,2-2y] και το αλλο [-1,0] για y και [-2-2y, 2+2y] για x ...ειναι σωστο ?
εδιτ : τυπογραφικο , εγραψα -x κατα λαθος αντι για -2 στο δευτερο οριο για x κ αλλαξα λιγο τ ορια γτ ειχα μπερδεψει τις ευθειες..
εδιτ : τυπογραφικο , εγραψα -x κατα λαθος αντι για -2 στο δευτερο οριο για x κ αλλαξα λιγο τ ορια γτ ειχα μπερδεψει τις ευθειες..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 11:51:26 am
στο θεμα 2(α) του ιουνη του '14 τι ορια πηρατε ?? το σπασα σε αθροισμα 2 ολοκληρωματων το ενα με ορια [0,1]για y και για x [-2+2y,2-2y] και το αλλο [-1,0] για y και [-2-2y, 2+2y] για x ...ειναι σωστο ?
εδιτ : τυπογραφικο , εγραψα -x κατα λαθος αντι για -2 στο δευτερο οριο για x κ αλλαξα λιγο τ ορια γτ ειχα μπερδεψει τις ευθειες..
Nομιζω ειναι 2 ολοκληρωματα.Το ενα [-2,0][-2-2ψ,2ψ-2]δχδψ και το αλλο [0,2][2ψ+2,2-2ψ]δχδψεδιτ : τυπογραφικο , εγραψα -x κατα λαθος αντι για -2 στο δευτερο οριο για x κ αλλαξα λιγο τ ορια γτ ειχα μπερδεψει τις ευθειες..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2015, 12:07:00 pm
μηπως το y παει απο [-1,1] ? γτ αν καταλαβα σωστα παιρνεις μια το αριστερα τριγωνο (αριστερα απο τον y'y) αυτο που σχηματιζεται δλδ με τις ευθειες x=-2+2y, x=-2-2y και τον αξονα y'y και μια το δεξια τριγωνο με τον y και τις αλλες ευθειες ..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 13, 2015, 12:37:51 pm
Για τον ιούνιο του 15 κάποια βοήθεια για το 4β?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 12:40:51 pm
μηπως το y παει απο [-1,1] ? γτ αν καταλαβα σωστα παιρνεις μια το αριστερα τριγωνο (αριστερα απο τον y'y) αυτο που σχηματιζεται δλδ με τις ευθειες x=-2+2y, x=-2-2y και τον αξονα y'y και μια το δεξια τριγωνο με τον y και τις αλλες ευθειες ..
Tα ορια προκυπτουν απο την προβολη του χωριου στον χ'χ αξονα.Αρα απο -2 εως 2.Αντιστοιχα αν ηταν κανονικο ως προς χ τα ορια θα ηταν απο -1 εως 1.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Algemar on September 13, 2015, 12:46:25 pm
Tα ορια προκυπτουν απο την προβολη του χωριου στον χ'χ αξονα.Αρα απο -2 εως 2.
Αντιστοιχα αν ηταν κανονικο ως προς χ τα ορια θα ηταν απο -1 εως 1.
Αντιστοιχα αν ηταν κανονικο ως προς χ τα ορια θα ηταν απο -1 εως 1.
Νομιζω πιο πανω, οταν εγραψες τα ολοκληρωματα, πηρες κανονικοτητα ως προς x, αρα τα ορια του y θα επρεπε να ειναι απο -1 εως 1, σωστα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 12:56:10 pm
Tα ορια προκυπτουν απο την προβολη του χωριου στον χ'χ αξονα.Αρα απο -2 εως 2.
Αντιστοιχα αν ηταν κανονικο ως προς χ τα ορια θα ηταν απο -1 εως 1.
Αντιστοιχα αν ηταν κανονικο ως προς χ τα ορια θα ηταν απο -1 εως 1.
Νομιζω πιο πανω, οταν εγραψες τα ολοκληρωματα, πηρες κανονικοτητα ως προς x, αρα τα ορια του y θα επρεπε να ειναι απο -1 εως 1, σωστα;
εγω πηρα κανονικο ως προς ψ αρα ορια για χ -2 εως 2
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ktsiolis on September 13, 2015, 13:02:59 pm
Θέμα 4ο Ιούνιος 2015, ερώτημα β....ξέρει κανείς πώς χρησιμοποιούμε το επικαμπύλιο για να βρούμε το βαθμωτό δυναμικό????
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Algemar on September 13, 2015, 13:10:05 pm
εγω πηρα κανονικο ως προς ψ αρα ορια για χ -2 εως 2
Αν παρεις κανονικοτητα ως προς y, τοτε τα ορια του y δεν θα πρεπε να ειναι συναρτησει του x; Ή τα χω μπερδεψει εντελως;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2015, 13:11:13 pm
νομιζω πως ναι, αν παρεις ως προς y κανονικοτητα τα ορια ως προς x πανε ( του dy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: menelaos619 on September 13, 2015, 13:57:01 pm
Παιδια για το θεμα 5ο του ιουνιου 2015 καμια ιδεα?
Το διανυσμα n πως προκυπτει?
Το διανυσμα n πως προκυπτει?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 16:37:39 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 16:45:44 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 17:03:30 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Δεκτό ότι δεν έχεις τα μέσα. Σαν λογική πάντως οτι μπορεί να έχεις λάθη, είναι προτιμότερο να τα ανεβάσεις και να σου βρει κάποιος το λάθος παρά να μην το βρεις καθόλου. Τέσπα, θα καθαρογράψω κάποια πράγματα και θα ανεβάσω ότι έχω λύσει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 17:05:33 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Δεκτό ότι δεν έχεις τα μέσα. Σαν λογική πάντως οτι μπορεί να έχεις λάθη, είναι προτιμότερο να τα ανεβάσεις και να σου βρει κάποιος το λάθος παρά να μην το βρεις καθόλου. Τέσπα, θα καθαρογράψω κάποια πράγματα και θα ανεβάσω ότι έχω λύσει.
Επισης μπορει καποιος να πει πως αποδεικνυω στο 4α του 15 οτι το πεδιο ειναι γραμμικο?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 13, 2015, 17:08:06 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Δεκτό ότι δεν έχεις τα μέσα. Σαν λογική πάντως οτι μπορεί να έχεις λάθη, είναι προτιμότερο να τα ανεβάσεις και να σου βρει κάποιος το λάθος παρά να μην το βρεις καθόλου. Τέσπα, θα καθαρογράψω κάποια πράγματα και θα ανεβάσω ότι έχω λύσει.
Επισης μπορει καποιος να πει πως αποδεικνυω στο 4α του 15 οτι το πεδιο ειναι γραμμικο?
Αρκεί να το γράψεις στη μορφή Αu με Α πίνακα 3x3 kai u=[x y z]T
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 17:29:07 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Δεκτό ότι δεν έχεις τα μέσα. Σαν λογική πάντως οτι μπορεί να έχεις λάθη, είναι προτιμότερο να τα ανεβάσεις και να σου βρει κάποιος το λάθος παρά να μην το βρεις καθόλου. Τέσπα, θα καθαρογράψω κάποια πράγματα και θα ανεβάσω ότι έχω λύσει.
Επισης μπορει καποιος να πει πως αποδεικνυω στο 4α του 15 οτι το πεδιο ειναι γραμμικο?
Αρκεί να το γράψεις στη μορφή Αu με Α πίνακα 3x3 kai u=[x y z]T
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 17:38:24 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 13, 2015, 17:40:04 pm
Δεν καταλαβαίνω γιατί αφού έχετε λύσει ότι έχετε λύσει δεν τα ανεβάζετε.
Προσωπικα α)γιατι δεν εχω σκανερ/κινητο με φωτογραφικη και β)γιατι αν δεις και απο τα πανω ποστ εχω κανει λαθαρες τρελες :D
Δεκτό ότι δεν έχεις τα μέσα. Σαν λογική πάντως οτι μπορεί να έχεις λάθη, είναι προτιμότερο να τα ανεβάσεις και να σου βρει κάποιος το λάθος παρά να μην το βρεις καθόλου. Τέσπα, θα καθαρογράψω κάποια πράγματα και θα ανεβάσω ότι έχω λύσει.
Επισης μπορει καποιος να πει πως αποδεικνυω στο 4α του 15 οτι το πεδιο ειναι γραμμικο?
Αρκεί να το γράψεις στη μορφή Αu με Α πίνακα 3x3 kai u=[x y z]T
Ίσως να είναι ισοδύναμο αυτό που λες. . Επίσης ο Α πρεπει να ειναι σταθερός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 17:51:07 pm
Στις λυσεις ιουνιος 14 Ατρεας που ανεβηκαν εδω στην ασκηση 5β γιατι στο ολοκληρωμα εχει 2 μπροστα ?(γραφει συμμετρια ή κατι τετοιο δεν φαινεται καλα)
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 17:52:15 pm
Στις λυσεις ιουνιος 14 Ατρεας που ανεβηκαν εδω στην ασκηση 5β γιατι στο ολοκληρωμα εχει 2 μπροστα ?(γραφει συμμετρια ή κατι τετοιο δεν φαινεται καλα)
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ιskandar νμζ εσυ τις ανεβασες ε ? κανε ενα κοπο δες το. ;)Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 17:54:32 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
και εμενα 65π/4 μου βγηκε στην αρχη και δεν πιστευα :DTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 13, 2015, 17:59:29 pm
Στις λυσεις ιουνιος 14 Ατρεας που ανεβηκαν εδω στην ασκηση 5β γιατι στο ολοκληρωμα εχει 2 μπροστα ?(γραφει συμμετρια ή κατι τετοιο δεν φαινεται καλα)
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ιskandar νμζ εσυ τις ανεβασες ε ? κανε ενα κοπο δες το. ;)Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ξέχνα το δυαρι και τη συμμετρία, είναι λ΄θος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 18:02:55 pm
Στις λυσεις ιουνιος 14 Ατρεας που ανεβηκαν εδω στην ασκηση 5β γιατι στο ολοκληρωμα εχει 2 μπροστα ?(γραφει συμμετρια ή κατι τετοιο δεν φαινεται καλα)
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ιskandar νμζ εσυ τις ανεβασες ε ? κανε ενα κοπο δες το. ;)Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ξέχνα το δυαρι και τη συμμετρία, είναι λ΄θος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2015, 18:03:37 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: AckermanMik on September 13, 2015, 18:06:58 pm
Στις λυσεις ιουνιος 14 Ατρεας που ανεβηκαν εδω στην ασκηση 5β γιατι στο ολοκληρωμα εχει 2 μπροστα ?(γραφει συμμετρια ή κατι τετοιο δεν φαινεται καλα)
Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ιskandar νμζ εσυ τις ανεβασες ε ? κανε ενα κοπο δες το. ;)Μπορει οποιος ειχε ανεβασει τις λυσεις ή οποιοσδηποτε να μας πει ?
Ξέχνα το δυαρι και τη συμμετρία, είναι λ΄θος
Θαρρω
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 18:12:51 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
ΛΕΠΟΝ έντιτ. όπως και να το πάρεις θα σου βγάλει π. ένα διάστημα π ολοκληρώνεις και στις 2 περιπτώσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 13, 2015, 18:13:06 pm
εντιτ: το β ολο λαθος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ailouros on September 13, 2015, 18:36:50 pm
Όταν αλλάζει το κέντρο της σφαίρας πως το λύνουμε?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 13, 2015, 18:55:50 pm
το β ειναι οταν εχει αλλαξει το κεντρο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xameno kormi on September 13, 2015, 19:07:02 pm
Σύμφωνα με μια ασκηση που έκανε ο Ατρέας στο τελευταίο μάθημα και κατι σημείωσεις στα downloads 5ο του Ιουνίου 15(και 14 με παρομοιο τροπο) πρέπει να λύνεται κάπως ετσι
αν δεν το εχω κανει ολο λαθος
δεν καταλαβαινω , πως προκυπτει το n0 ? αν δεν το εχω κανει ολο λαθος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 13, 2015, 19:24:26 pm
Όταν έκανε ο Ατρέας παρόμοια άσκηση είχε πει οτι n0=+-r(διανυσμα)/R για σφαίρα. Τώρα αν μπορούμε να το πάρουμε κατευθείαν η αν θα πρέπει να το αποδείξουμε φαντάζομαι ότι μπορουμε να το πάρουμε κατευθειαν.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zumo naranja on September 13, 2015, 19:31:56 pm
Σύμφωνα με μια ασκηση που έκανε ο Ατρέας στο τελευταίο μάθημα και κατι σημείωσεις στα downloads 5ο του Ιουνίου 15(και 14 με παρομοιο τροπο) πρέπει να λύνεται κάπως ετσι
αν δεν το εχω κανει ολο λαθος
αν δεν το εχω κανει ολο λαθος
Nα σου πω, τι αλλαζει και λυνεις με 2 διαφορετικους τροπους το α) και το β)?
Στο β) λες οτι το Ο ανηκει στη σφαιρα, αλλα εγω απ οτι βλεπω δεν ανηκει.
Δεδομενου ομως οτι εσυ θεωρεις οτι επισης ανηκει, τι σε κανει να τα λυνεις διαφορετικα?
Οσο για το n0, ειναι το αναδελτα της επιφανειας για την οποια θελουμε να το βρουμε. Στην προκειμενη ειναι (2x,2y,2z)/(το μετρο του διανυσματος), συνεπως ειναι μετα απο λιγες πραξεις r διανυσμα δια r μετρο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: bsp on September 13, 2015, 19:43:50 pm
Μεγάλη μαλακία έκανα εχεις δίκιο, Το (0,0,0) δεν ανήκει στην σφαίρα αλλά και να άνηκε όλα αυτα που κάνω είναι ανούσια. Γράψτε λάθος και σορυ για το μπέρδεμα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Laharl on September 13, 2015, 19:44:48 pm
Στο 1ο θεμα του 2014 που λεει να χαρακτηρισουμε τα στασιμα σημεια, υπαρχει τροπος να γινει χωρις να ψαχνουμε την οριζουσα του πινακα( εδω αφου εχουμε 3 μεταβλητες θα ειναι 3Χ3). Δηλαδη να μην παμε με τον πατροπαραδοτο τροπο εξετασης fxx και DetH
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 19:53:45 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
ΛΕΠΟΝ έντιτ. όπως και να το πάρεις θα σου βγάλει π. ένα διάστημα π ολοκληρώνεις και στις 2 περιπτώσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: gioti488 on September 13, 2015, 20:06:03 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:07:43 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
ΛΕΠΟΝ έντιτ. όπως και να το πάρεις θα σου βγάλει π. ένα διάστημα π ολοκληρώνεις και στις 2 περιπτώσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on September 13, 2015, 20:11:33 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
ΛΕΠΟΝ έντιτ. όπως και να το πάρεις θα σου βγάλει π. ένα διάστημα π ολοκληρώνεις και στις 2 περιπτώσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:12:36 pm
Στο Θέμα 3 Ιουν 2015 τα όρια ολοκλήρωσης είναι : R από 2 εως 3, θ από 0 εως π και φ από 0 εώς π/2. Ουσιαστικά από τον περιορισμό χ,z>0 καταλαβαίνω ότι ολοκληρώνω στο 1/4 σφαίρας στον τομέα R 2εώς3. Και αν δεν έχω κάνει λάθος στις πράξεις πρέπει να βγαίνει 16,25π
μηπως το θ παει απο -π/2 εως π/2 ? στην ουσια ειναι η προβολη στο Οxy αρα θες x>0 που ειναι απο -π/2 εως π/2 ε ??
ΛΕΠΟΝ έντιτ. όπως και να το πάρεις θα σου βγάλει π. ένα διάστημα π ολοκληρώνεις και στις 2 περιπτώσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:14:13 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Όταν det|Hf|<0 το σημείο σου είναι σαγματικό. Και επίσης έχουμε βρει διαφορετικά α,b αλλά μαλλον οφείλετε σε πράξεις. Το τριπλό-ολοκλήρωμα το έχουμε ίδιο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: gioti488 on September 13, 2015, 20:16:12 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Όταν det|Hf|<0 το σημείο σου είναι σαγματικό. Και επίσης έχουμε βρει διαφορετικά α,b αλλά μαλλον οφείλετε σε πράξεις. Το τριπλό-ολοκλήρωμα το έχουμε ίδιο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zumo naranja on September 13, 2015, 20:25:36 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Για το 1β, εισαι σιγουρη για το α που βρισκεις? Λεει οτι θες να εχεις την κατευθυνση της εφαπτομενης της καμπυλης, αλλα εσυ αυτο που βρισκεις ειναι το καθετο διανυσμα στην καμπυλη.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:40:53 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Για το 1β, εισαι σιγουρη για το α που βρισκεις? Λεει οτι θες να εχεις την κατευθυνση της εφαπτομενης της καμπυλης, αλλα εσυ αυτο που βρισκεις ειναι το καθετο διανυσμα στην καμπυλη.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:46:02 pm
Πρόοδος 14 υπάρχουν λάθη στις λυσεις που δεν έχω διορθώσει αλλά επί των πλείστων έχουν συζητηθεί εδώ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:48:36 pm
Ιούνιος 14 ατρέας
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 20:50:14 pm
Ιούνιος 14 Ξένος
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 20:54:59 pm
Ιούνιος 14 Ξένος
εισαι σωστοτατος! ^beer^Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 21:17:41 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Στο 1α, εγω ειχα παρει το οτι f(0,0)=2 ως δεδομενο, γιατι θεωρησα τραβηγμενο να μου δωσει 3βαθμια να λυσω.Ολα μου φαινονται μια χαρα.
εδιτ: στο 2α, το β ειναι -2 η -10? γιατι η εξισωση που βγαζω εγω ειναι 5α-β-5(α+2)=0=>-β-10=0=>β=-10
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 21:22:25 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Στο 1α, εγω ειχα παρει το οτι f(0,0)=2 ως δεδομενο, γιατι θεωρησα τραβηγμενο να μου δωσει 3βαθμια να λυσω.Ολα μου φαινονται μια χαρα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: zumo naranja on September 13, 2015, 21:25:08 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Στο 1α, εγω ειχα παρει το οτι f(0,0)=2 ως δεδομενο, γιατι θεωρησα τραβηγμενο να μου δωσει 3βαθμια να λυσω.Ολα μου φαινονται μια χαρα.
Ναι, ναι. Εγω ειδα ποιος ειναι ο κυκλος που μας δινει, και ειδα οτι στο (0,0) "ακουμπαει" αρα η εφαπτομενη του εκει θα ειναι η y=0, και επειδη μας λεει με κατευθυνση τα θετικα x πηρα ως α το (1,0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 21:29:34 pm
Επισυνάπτω κάποια από τα θέματα Ιούνη 2015.Λείπει το 4β και το 5.Δεν ξέρω αν είναι σωστά.Δείτε και πείτε μου.
Στο 1α, εγω ειχα παρει το οτι f(0,0)=2 ως δεδομενο, γιατι θεωρησα τραβηγμενο να μου δωσει 3βαθμια να λυσω.Ολα μου φαινονται μια χαρα.
Ναι, ναι. Εγω ειδα ποιος ειναι ο κυκλος που μας δινει, και ειδα οτι στο (0,0) "ακουμπαει" αρα η εφαπτομενη του εκει θα ειναι η y=0, και επειδη μας λεει με κατευθυνση τα θετικα x πηρα ως α το (1,0)
Πάμε μια από την αρχή. Μπορείς να εξηγήσεις λίγο πως την έλυσες εσύ? Σε έχασα κάπου
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alice_8 on September 13, 2015, 21:32:14 pm
Στο 1.β-Ιούνιος 2015: Η καμπύλη της οποίας μας ζητάει την εφαπτομένη, είναι κύκλος, με κέντρο το σημείο (0,2) και ακτίνα 2.Άρα η εφαπτομένη του στο σημείο (0,0) είναι ο άξονας χ'χ . Άρα το μοναδιαίο ορθογώνιο διάνυσμα που ψάχνουμε, θα είναι το μοναδιαίο του χ, δηλαδή το (1,0) .
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 21:36:35 pm
Στο 1.β-Ιούνιος 2015: Η καμπύλη της οποίας μας ζητάει την εφαπτομένη, είναι κύκλος, με κέντρο το σημείο (0,2) και ακτίνα 2.Άρα η εφαπτομένη του στο σημείο (0,0) είναι ο άξονας χ'χ . Άρα το μοναδιαίο ορθογώνιο διάνυσμα που ψάχνουμε,δεν θα είναι το μοναδιαίο του χ, δηλαδή το (1,0) ? Κάνω λάθος?
Ωραία συμφωνώ διαισθητικά. Μαθηματικά πως το βρίσκουμε αυτό?Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alice_8 on September 13, 2015, 21:41:41 pm
Μαθηματικά το έχεις βρει, αφού σου δίνει: 1) την καμπύλη της οποίας θέλεις να υπολογίσεις την εφαπτομένη (εδώ ο κύκλος) 2)το σημείο στο οποίο θέλεις να την υπολογίσεις (εδώ το (0,0) ) 3) την κατεύθυνση (εδώ τα θετικά του x'x) και 4)ξέρεις πως το διάνυσμα που ψάχνεις πρέπει να είναι ορθογώνιο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 21:43:13 pm
Μαθηματικά το έχεις βρει, αφού σου δίνει: 1) την καμπύλη της οποίας θέλεις να υπολογίσεις την εφαπτομένη (εδώ ο κύκλος) 2)το σημείο στο οποίο θέλεις να την υπολογίσεις (εδώ το (0,0) ) 3) την κατεύθυνση (εδώ τα θετικά του x'x) και 4)ξέρεις πως το διάνυσμα που ψάχνεις πρέπει να είναι ορθογώνιο.
Nα στο θέσω αλλίως έχω μια καμπύλη C kai θέλω να βρω το εφαπτόμενο διάνυσμα της σε ένα σημείο. Πως το κάνω αυτόTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alice_8 on September 13, 2015, 21:54:15 pm
Έχω βρεi την εξίσωση του εφαπτόμενου επιπέδου σε σημείο P(x0,y0,z0) καμπύλης S με εξίσωση έστω F (δεν ξέρω αν είναι το ίδιο για εφ.ευθεία) :
(dF/dx)*(x-x0) +(dF/dy)*(y-y0) + (dF/dz)*(z-z0)= 0 όπου τα (dF/dx),(dF/dy),(dF/dz) υπολογισμένα στο σημείο P.
(dF/dx)*(x-x0) +(dF/dy)*(y-y0) + (dF/dz)*(z-z0)= 0 όπου τα (dF/dx),(dF/dy),(dF/dz) υπολογισμένα στο σημείο P.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 21:57:37 pm
Έχω βρεi την εξίσωση του εφαπτόμενου επιπέδου σε σημείο P(x0,y0,z0) καμπύλης S με εξίσωση έστω F (δεν ξέρω αν είναι το ίδιο για εφ.ευθεία) :
(dF/dx)*(x-x0) +(dF/dy)*(y-y0) + (dF/dz)*(z-z0)= 0 όπου τα (dF/dx),(dF/dy),(dF/dz) υπολογισμένα στο σημείο P.
(dF/dx)*(x-x0) +(dF/dy)*(y-y0) + (dF/dz)*(z-z0)= 0 όπου τα (dF/dx),(dF/dy),(dF/dz) υπολογισμένα στο σημείο P.
Η εξίσωση που βρήκες είναι η εξίσωση εφαπτόμενου επιπέδου στην καμπύλη S sto σημείο P. σελ 80 κεφ 3 σημειώσεις ατρέα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alice_8 on September 13, 2015, 22:03:05 pm
Ναι το ξέρω, το έγραψα πιο πάνω οτι είναι εξίσωση εφ .επιπέδου κ όχι εφ .ευθείας ,απλά μέχρι τώρα αυτό βρήκα μόνο!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 22:07:04 pm
Ναι το ξέρω, το έγραψα πιο πάνω οτι είναι εξίσωση εφ .επιπέδου κ όχι εφ .ευθείας ,απλά μέχρι τώρα αυτό βρήκα μόνο!
Έχω θολώσει. Αν το έχει λύσει κάποιος ας το ανεβάσει να το δούμε λυμένοTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 22:26:28 pm
Σας εχασα ρε μαγκες, ποιο θεμα συζηταμε?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 22:28:00 pm
Σας εχασα ρε μαγκες, ποιο θεμα συζηταμε?
Θέμα 1β 2015. το διάνυσμα α που παίρνουμε εμείς είναι λα΄θος διότι το grad σου δίνει το κάθετο διάνυσμα και όχι το παράλληλοTitle: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 22:40:37 pm
η κατευθυνση της εφαπτομενης της g ειναι grad,οχι?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Give_Life_Back on September 13, 2015, 22:47:55 pm
η κατευθυνση της εφαπτομενης της g ειναι grad,οχι?
Όχι από ότι κατάλαβα. Το grad δίνει το κάθετο. και αν το δεις και σχηματικά όπως το εξηγεί το παιδί από πάνω το διάνυσμα α πρεέπει να είναι το (1,0) και όχι το (0,-1)Πάρτε και 4/β 2015
και 5/α και 5/β/ii
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Alice_8 on September 13, 2015, 22:49:40 pm
Νομίζω πως όλα τα υπόλοιπα στο θέμα αυτό είναι σωστά έτσι όπως είναι ανεβασμένα με ένα λάθος στις πράξεις μόνο. Αυτό που αλλάζει είναι οτι δεν βρίσκεις το διάνυσμα a έτσι όπως είναι στα ανεβασμένα , αλλά θεωρείς οτι είναι το (1,0) .
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on September 13, 2015, 23:44:24 pm
Τα επαιξα και παω για μπυρα αδερφια. Καλη τυχη αυριο!
υ.γ. ακομα ειμαι πεπεισμενος οτι το gradf δινει το εφαπτομενικο διανυσμα. Αν οχι μπορει να παιζει κατι με τα Py, Qx απο το 3ο κεφαλαιο
Καλη συνεχεια ωρε γενναιοι
υ.γ. ακομα ειμαι πεπεισμενος οτι το gradf δινει το εφαπτομενικο διανυσμα. Αν οχι μπορει να παιζει κατι με τα Py, Qx απο το 3ο κεφαλαιο
Καλη συνεχεια ωρε γενναιοι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vlassis on September 15, 2015, 11:21:56 am
Λύσεις από τα θέματα του Σεπτεμβρίου 2015, δεν είναι δικές μου απλά τις ανεβάζω για μελλοντική χρήση! :)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: boone on February 07, 2016, 23:32:24 pm
Πως βγαινει η γωνια φ στο τριτο θεμα;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: JakeLaMotta on February 08, 2016, 00:57:13 am
Πως βγαινει η γωνια φ στο τριτο θεμα;;
Εγώ πάντως το σκέφτηκα ως εξής:
Παίρνω κυλινδρικές συντεταγμένες,με όρια για το θ [0,2π),για το ρ (0,6) επειδή x^2+y^2=6 και για το z από (0,sqrt(9-x^2-y^2).Έχει κάποιες ασκήσεις που λύνονται κάπως έτσι στο κεφ.5 στις σημειώσεις του Ατρέα,για τριπλά ολοκληρώματα.
Δεν ξέρω αν είναι σωστό,αλλά κι εγώ δεν μπορούσα να καταλάβω τι ακριβώς κάνει με τη γωνία οπότε έπρεπε να βρω κάτι άλλο...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: boone on February 08, 2016, 01:10:03 am
Πως βγαινει η γωνια φ στο τριτο θεμα;;
Εγώ πάντως το σκέφτηκα ως εξής:
Παίρνω κυλινδρικές συντεταγμένες,με όρια για το θ [0,2π),για το ρ (0,6) επειδή x^2+y^2=6 και για το z από (0,sqrt(9-x^2-y^2).Έχει κάποιες ασκήσεις που λύνονται κάπως έτσι στο κεφ.5 στις σημειώσεις του Ατρέα,για τριπλά ολοκληρώματα.
Δεν ξέρω αν είναι σωστό,αλλά κι εγώ δεν μπορούσα να καταλάβω τι ακριβώς κάνει με τη γωνία οπότε έπρεπε να βρω κάτι άλλο...
Βασικά, με λίγο ψάξιμο, είδα ότι το arcsin ειναι ουσιαστικό το τόξο της σφαιρας που οριοθετειται απο τον κύλινδρο, οπότε έχει μια βάση. Από κει και πέρα, αν πέσει κάτι παρόμοιο θα το πάρω σαν έτοιμο τύπο κι ας ελπίσουμε να πιάσει!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meow on June 07, 2016, 18:15:27 pm
γιατι στα downloads του λογισμου 2 σημειωσεις Ατρεα 2012-13 τις κατεβαζω αλλα δεν μπορω να τις ανοιξω?Οταν κανω το extract?HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nFin1ty on June 07, 2016, 18:30:45 pm
Πρέπει να κατεβάσεις και τα 7 part στον ίδιο φάκελο, να ανοίξεις ένα από αυτά και να κάνεις extract το pdf.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meow on June 07, 2016, 18:35:44 pm
Ευχαριστω παρα πολυ!!!!!!!!!!!!!!!!!!!!!!!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Meow on June 07, 2016, 19:46:37 pm
Το κατεβασα !!!Και ειναι 186 σελιδες!!!Yeah!! :D :D
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: isitsou on June 11, 2016, 15:49:06 pm
Στο θέμα 2 του Ιουνίου του 2014. Στο πρώτο ερώτημα, αφού το χωρίο ολοκλήρωσης είναι συμμετρικό και ως προς xx και ως προς yy δεν μπορούμε να πάρουμε 4 φορές το διπλό ολοκλήρωμα με όρια [0,1] και [0,2-2y]??? είδα και παλαιότερα ποστ(και τα λυμμένα που έχουν ανέβει) αλλά δεν έβγαλα και πολύ άκρη με τα όρια ολοκλήρωσης.... Βασικά έτσι όπως το λύνει στα λυμμένα που έχουν ανέβει χρειάζεται να υπολογίσεις 2 διπλά ολοκληρώματα ενώ λόγο συμμετρίας παίζει να λύνεται και μόνο με ένα ολοκλήρωμα....
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 14, 2016, 17:07:57 pm
Θεμα 2β σεπτεμβριος 15 ομαδα Α βρισκω 2 στασιμα Po = (0,0,1) και Ρο = (-2,2,1)
οπου το 1ο ειναι σαγματικο και το 2ο τοπικο μεγιστο.Βρηκε κανεις τα ιδια ?
οπου το 1ο ειναι σαγματικο και το 2ο τοπικο μεγιστο.Βρηκε κανεις τα ιδια ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: JasonTheModel on June 14, 2016, 19:46:03 pm
Θεμα 2β σεπτεμβριος 15 ομαδα Α βρισκω 2 στασιμα Po = (0,0,1) και Ρο = (-2,2,1)
οπου το 1ο ειναι σαγματικο και το 2ο τοπικο μεγιστο.Βρηκε κανεις τα ιδια ?
ναιοπου το 1ο ειναι σαγματικο και το 2ο τοπικο μεγιστο.Βρηκε κανεις τα ιδια ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasiliki_97 on June 15, 2016, 00:27:29 am
στο θεμα 2α ποσο βρηκατε τις μερικες παραγωγους?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konsta on June 15, 2016, 01:08:39 am
στο θεμα 2α ποσο βρηκατε τις μερικες παραγωγους?
εγω x ως προς z βρηκα -z/x+y ..
και αν ειναι σωστο η αλλη βγαινει αναλογα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: konsta on June 15, 2016, 01:14:14 am
σεπτ.15. ομαδα Α
βρηκαμε
1α) lim=0
1b) f(x,y)=x^4+y*(x^2)/2y^5+10
σωστο ??
βρηκαμε
1α) lim=0
1b) f(x,y)=x^4+y*(x^2)/2y^5+10
σωστο ??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DEVRIM on June 15, 2016, 11:49:48 am
εγω παντως βρηκα για το 1.β)
f(x,y)=x^4+y^5+((x*y)^2)/2+10
f(x,y)=x^4+y^5+((x*y)^2)/2+10
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: iSage on June 15, 2016, 18:48:23 pm
υπολογιζετε το θεμα 3 με διπλο ολοκληρωμα στο D: x^2+y^2=6 και f(x,y)=sqrt(9-x^2-y^2) ? (και παιρνουμε μετα το διπλασιο..)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on June 16, 2016, 15:38:10 pm
Στο θεμα 1α του Σεπτεμβρη '15, εχει λυσει καποιος το οριο με τα ημιτονα??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Perasmus on June 16, 2016, 16:04:48 pm
Στα Θεματα Ατρέα Ιούνιος 2013 , Θέμα 4α .
Απο παλιότερο post σ αυτό το topic κάποιος πόσταρε αυτή την λύση.
Δεν μπορώ να καταλάβω.. Χρειάζεται να γίνει η παραμετροποιήση ,,,;;;
Δεν μπορώ κατευθεία να πάω με πολικές συντεταγμενες;;
Απο παλιότερο post σ αυτό το topic κάποιος πόσταρε αυτή την λύση.
Δεν μπορώ να καταλάβω.. Χρειάζεται να γίνει η παραμετροποιήση ,,,;;;
Δεν μπορώ κατευθεία να πάω με πολικές συντεταγμενες;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: ChrisKaloy-Kakou on June 16, 2016, 16:09:25 pm
Στο θεμα 1α του Σεπτεμβρη '15, εχει λυσει καποιος το οριο με τα ημιτονα??
Πάρε μονοπάτια y=x και y=-x.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: leukosaraphs! on June 16, 2016, 16:11:01 pm
παρε 2 μονοπατια , εγω πηρα x=y και βρηκα 1/3 και x=-y και βρηκα 0 αρα δεν υπαρχει
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: leukosaraphs! on June 16, 2016, 16:26:28 pm
εγω παντως βρηκα για το 1.β)
f(x,y)=x^4+y^5+((x*y)^2)/2+10
f(x,y)=x^4+y^5+((x*y)^2)/2+10
Κοιτα μια την φωτο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on June 16, 2016, 17:43:51 pm
Απο Ιουνη 2014 Θεμα 1.β κανεις καμια ιδέα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on June 16, 2016, 19:04:34 pm
Θεμα 4β παλι Σεπτ. '15 κανεις?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Dimi97 on June 16, 2016, 19:43:04 pm
Θεμα 4β παλι Σεπτ. '15 κανεις?
Έχει ανεβάσει κάποιος μερικές σελίδες πίσω τις λύσεις, αλλα στις ξανα ανεβάζω
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: potirikolonato on June 16, 2016, 20:56:24 pm
Θεμα 5β Ιουνιο του 15 μπορει να ανεβασει κανεις λυση;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: airguitar on June 16, 2016, 21:06:52 pm
Θεμα 5β Ιουνιο του 15 μπορει να ανεβασει κανεις λυση;
https://www.dropbox.com/s/4tfeoxdap1ub4iv/%CE%91%CF%84%CF%81%CE%AD%CE%B1%CF%82%205.jpg?dl=0ειναι απο ιουνιο 14 αλλα λυνεται με τον ιδιο τροπο
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Endeavour X on June 16, 2016, 21:11:08 pm
Απο Ιουνη 2014 Θεμα 1.β κανεις καμια ιδέα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: potirikolonato on June 16, 2016, 21:12:13 pm
Χιλια ευχαριστώ !!!
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: leukosaraphs! on June 16, 2016, 21:19:27 pm
Quote
Απο Ιουνη 2014 Θεμα 1.β κανεις καμια ιδέα;
Αν θεωρησεις dF=Fxdx+Fydy+Fudu+}F vdv
και αντικαστασεις τα dx ,dy με Χudv+Xvdv κι αντιστοιχα για dy μπορει να καταληξεις καπου
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on June 16, 2016, 22:26:40 pm
Πως δειχνω πως ενα πεδιο ειναι γραμμικο;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Σα τανυστής on June 16, 2016, 22:28:26 pm
αν γραφεται σε μορφη πινακα επι [ x y z ] , οπως στα σαε2 ενα πραμα αν εχεις κανει.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Dimi97 on June 16, 2016, 22:50:25 pm
Απο Ιουνη 2014 Θεμα 1.β κανεις καμια ιδέα;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: di_em on June 16, 2016, 23:12:57 pm
Θέμα 5ο ιουνιών '14 και '15 έχει ανεβάσει κανείς λύσεις ή μπορεί να διαφωτίσει? (για το (β))
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on June 16, 2016, 23:13:51 pm
Θέμα 5ο ιουνιών '14 και '15 έχει ανέβάσει κανείς λύσει ή μπορεί να διαφωτίσει?
+1
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: leukosaraphs! on June 16, 2016, 23:36:10 pm
για το θεμα 5 ιουνιου του 15
α) θεωρεις παραμετροποιηση r(u,v)=(u,v,u^2+v^2)
βρισκεις καθετο διανυσμα n=(-2u,-2v,1)
παιρνεις το μετρο του |n|=sqrt(1+4(u^2+v^2))
λυνεις το ολοκληρωμα , εγω το κανα με πολικες συντεταγμενες
β) πρωτη βουλιτσα:
λες οτι το θεωρημα Gauss δεν ισχυει γτ εχεις ανωμαλο σημειο το (0,0,0) αρα θεωρεις σφαιρα x^2+y^2+z^2=ε^2 , εφαρμοζεις γενικευμενο θεωρημα Gauss στο οποιο καταληγεις σε 2 ολοκληρωματα , το δευτερο ειναι 0 (γιατι το div(F)=0) και ετσι εχεις να υπολογισεις το επιφανειακο πανω στην σφαιρα που θεωρησες , με μια απλη αλλαγη σε σφαιρικες βγαινει
δευτερη βουλιτσα:
ισχυει το θεωρημα Gauss αρα 0 (γιατι div(F)=0)
α) θεωρεις παραμετροποιηση r(u,v)=(u,v,u^2+v^2)
βρισκεις καθετο διανυσμα n=(-2u,-2v,1)
παιρνεις το μετρο του |n|=sqrt(1+4(u^2+v^2))
λυνεις το ολοκληρωμα , εγω το κανα με πολικες συντεταγμενες
β) πρωτη βουλιτσα:
λες οτι το θεωρημα Gauss δεν ισχυει γτ εχεις ανωμαλο σημειο το (0,0,0) αρα θεωρεις σφαιρα x^2+y^2+z^2=ε^2 , εφαρμοζεις γενικευμενο θεωρημα Gauss στο οποιο καταληγεις σε 2 ολοκληρωματα , το δευτερο ειναι 0 (γιατι το div(F)=0) και ετσι εχεις να υπολογισεις το επιφανειακο πανω στην σφαιρα που θεωρησες , με μια απλη αλλαγη σε σφαιρικες βγαινει
δευτερη βουλιτσα:
ισχυει το θεωρημα Gauss αρα 0 (γιατι div(F)=0)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Egkelados on September 04, 2016, 17:57:50 pm
Στα θέματα του Ιουνίου του 2016 στο 2ο θέμα στο β ερώτημα πως ακριβώς βρίσκω τα σημεία? καταλήγω να βρίσκω w = 0 ενώ έχω πει ότι τα v,w είναι μη μηδενικά και κολλάω εκεί.
Θέμα http://prntscr.com/ce0xaq (http://prntscr.com/ce0xaq)
Το έχω φτάσει ως εδώ : http://prntscr.com/ce116a (http://prntscr.com/ce116a) http://prntscr.com/ce15sk (http://prntscr.com/ce15sk)
Θέμα http://prntscr.com/ce0xaq (http://prntscr.com/ce0xaq)
Το έχω φτάσει ως εδώ : http://prntscr.com/ce116a (http://prntscr.com/ce116a) http://prntscr.com/ce15sk (http://prntscr.com/ce15sk)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Σα τανυστής on September 04, 2016, 18:09:06 pm
Σορρυ που πεταγομαι λιγο οφτοπικ, αλλα επειδη εβγαλα βαθμο με ~3-4 μερες διαβασμα και σε βλεπω οτι εχεις αποριες συγκεκριμενες σε ασκησεις μπορεις απλα να πας στον ατρεα με αυτες. Ετσι εκανα εγω, και καταληξαμε να μου κανει ιδιαιτερο ουσιαστικα ( ο τυπος ειναι ο,τι καλυτερο εχει συμβει στο ΤΗΜΜΥ). Οποτε μαζεψε κανα 5-10 ασκησεις και πηγαινε οσο ειναι καιρος.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Egkelados on September 04, 2016, 18:31:48 pm
να σου πω την αλήθεια δεν το σκέφτηκα καθόλου γιατί μέχρι στιγμής ότι απορία είχα λυνόταν με τη βοήθεια άλλων παιδιών αλλά ίσως να το κάνω αυτό που λες σίγουρα θα βοηθήσει
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: stkintzo on September 06, 2016, 23:15:49 pm
Στα θέματα του Ιουνίου του 2016 στο 2ο θέμα στο β ερώτημα πως ακριβώς βρίσκω τα σημεία? καταλήγω να βρίσκω w = 0 ενώ έχω πει ότι τα v,w είναι μη μηδενικά και κολλάω εκεί.
Θέμα http://prntscr.com/ce0xaq (http://prntscr.com/ce0xaq)
Το έχω φτάσει ως εδώ : http://prntscr.com/ce116a (http://prntscr.com/ce116a) http://prntscr.com/ce15sk (http://prntscr.com/ce15sk)
Aδερφε εγω ετσι το εβγαλα.τσεκαρε.Ελπιζω να μαι σωστος.Θέμα http://prntscr.com/ce0xaq (http://prntscr.com/ce0xaq)
Το έχω φτάσει ως εδώ : http://prntscr.com/ce116a (http://prntscr.com/ce116a) http://prntscr.com/ce15sk (http://prntscr.com/ce15sk)
Κινηθηκα συμφωνα με σελ 91 ατρεα.
http://prntscr.com/ceyca2
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Egkelados on September 07, 2016, 01:08:21 am
Καλό φαίνεται ναι! Είδα ένα παιδί που για να βρεί τα σημεία επειδή βόλευε έκανε απλά αντικατάσταση στην f(x,y) το y2 το οποίο το βρίσκεις από τη g(x,y) με τι ισούται και μετά βρήκε τα 2 σημεία αλλά το δικό σου πιο σωστό μου φαίνεται! Ευχαριστώ κιόλας
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on February 06, 2017, 01:03:13 am
Μιας και πλησιαζει η μερα, εχει λυσει καποιος τα θεματα ιουνιου '16; Με ενδιαφερουν κυριως τα θεματα 3,4,5
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: HAL 9000 on February 06, 2017, 03:15:25 am
Μιας και πλησιαζει η μερα, εχει λυσει καποιος τα θεματα ιουνιου '16; Με ενδιαφερουν κυριως τα θεματα 3,4,5
Υπάρχουν ανεβασμένες λύσεις του Ιουνίου του 16 στα downloads από ένα παιδί.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Perasmus on February 07, 2017, 15:04:27 pm
Καλησπέρα! :) Κάποιος συνάδελφος ανέβασε στο τόπικ τις λύσεις αυτές.
Για Θέμα 2α απο Σεπτέμβριο 2015.
Είναι σωστή αυτή η λύση;; Βρήκε κάποιος καποιον άλλον τρόπο;;
Για Θέμα 2α απο Σεπτέμβριο 2015.
Είναι σωστή αυτή η λύση;; Βρήκε κάποιος καποιον άλλον τρόπο;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Perasmus on February 07, 2017, 21:34:54 pm
Επίσης το Θέμα 3 του Σεπτεμβρίου 2016 λύνεται με 3πλο ολοκλήρωμα φαντάζομαι. Τα όρια ολοκλήρωσης για το z ποιά είναι;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Niobe on February 09, 2017, 22:45:15 pm
Επίσης το Θέμα 3 του Σεπτεμβρίου 2016 λύνεται με 3πλο ολοκλήρωμα φαντάζομαι. Τα όρια ολοκλήρωσης για το z ποιά είναι;;
+1
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MrRobot on February 10, 2017, 00:30:53 am
Επίσης το Θέμα 3 του Σεπτεμβρίου 2016 λύνεται με 3πλο ολοκλήρωμα φαντάζομαι. Τα όρια ολοκλήρωσης για το z ποιά είναι;;
Χωρίς να το έχω λύσει μέχρι τέλους πιστεύω ότι επειδη η πυκνότητα φορτίου εξαρτάται μόνο από τα x, y μπορείς να μεταφέρεις τη σφαίρα όπου θέλεις στον άξονα z. Δηλαδή μπορείς να χρησιμοποιήσεις τη σφαίρα x2 + y2 + z2 = 9 αντί για αυτή που σου δίνει. Μετά χρησιμοποίησε πολικές συντενταγμένες για πιο εύκολη ολοκλήρωση.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Professor on June 18, 2017, 17:23:42 pm
Εχει λυσει κανεις το 6ο θεμα απο τον Σεπτεμβρη '16? :(
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Singularity on September 07, 2017, 13:55:52 pm
στο θέμα 5 στο γραπτό του 2016 ομάδα Α έχουμε ότι το έργο στην καμπύλη ΑΒγ είναι 1 με την συμβατική φορά κάνουμε το επικαμπύλιο στην ΑΒ με παραμετροποίηση βρίσουμε ότι είναι -3/2 άρα το έργο του πεδίου στην γ θα είναι ίσο με +5/2?
επίσης καθώς δεν ορίζετε ποια φορά θα πρέπει να ακολουθήσουμε στη καμπύλη γ μήπως θα έπρεπε να δώσουμε 2 τιμές για το έργο η μία να είναι 5/2 για την συμβατική φορά και μια η οποία με αντίστρεψη των ορίων του επικαμπύλιου στο ΑΒ θα βγεί -5/2 στο γ? κάτι που βγάζει νόημα αφου για κάθε dxdy και dt αντίστοιχα θα έχουμε ένα - μπροστά?
επίσης καθώς δεν ορίζετε ποια φορά θα πρέπει να ακολουθήσουμε στη καμπύλη γ μήπως θα έπρεπε να δώσουμε 2 τιμές για το έργο η μία να είναι 5/2 για την συμβατική φορά και μια η οποία με αντίστρεψη των ορίων του επικαμπύλιου στο ΑΒ θα βγεί -5/2 στο γ? κάτι που βγάζει νόημα αφου για κάθε dxdy και dt αντίστοιχα θα έχουμε ένα - μπροστά?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Prison Mike on September 10, 2017, 14:15:40 pm
Κάπιος μήπως θα μπορούσε να βοηθήσει στο Θέμα 2) α) του ιουνίου 13 ?
edit by mod: λιγη προσοχη που κανουμε τα ποστ
edit by mod: λιγη προσοχη που κανουμε τα ποστ
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sabpap on September 10, 2017, 17:32:29 pm
Κάπιος μήπως θα μπορούσε να βοηθήσει στο Θέμα 2) α) του ιουνίου 13 ?
edit by mod: λιγη προσοχη που κανουμε τα ποστ
edit by mod: λιγη προσοχη που κανουμε τα ποστ
Στέλνω τη λύση μου..
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Prison Mike on September 10, 2017, 18:05:35 pm
Στέλνω τη λύση μου..
Ευχαριστώ για την λύση νομίζω εχεις ενα μικρό λαθάκι ομως στην Hf που κατασκεύσες. Βρήκες την Fzz ίση με -2 αλλα δεν την εβαλες την τιμή στον εσσιανό πίνακα αυτό αλλαζει λίγο τα πραγματα νομίζω! ::)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: sabpap on September 10, 2017, 19:10:34 pm
Ευχαριστώ για την λύση νομίζω εχεις ενα μικρό λαθάκι ομως στην Hf που κατασκεύσες. Βρήκες την Fzz ίση με -2 αλλα δεν την εβαλες την τιμή στον εσσιανό πίνακα αυτό αλλαζει λίγο τα πραγματα νομίζω! ::)
Έχεις δίκιο... τυχαίνει να βγαίνει και πάλι αρνητική η det(H), οπότε δεν αλλάζει κάτι...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: malappapas on September 10, 2017, 19:22:25 pm
Σεπτεμβρης 16 Ομαδα Β, το θεμα 4 πως το αποδεικνυω;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Prison Mike on September 10, 2017, 19:34:13 pm
Έχεις δίκιο... τυχαίνει να βγαίνει και πάλι αρνητική η det(H), οπότε δεν αλλάζει κάτι...
Ναι όντως ευχαρίστώ !
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Apostolof on September 10, 2017, 22:18:58 pm
Σεπτεμβρης 16 Ομαδα Β, το θεμα 4 πως το αποδεικνυω;
Στο συνημμένο.
Στο θέμα 2 Σεπτέμβρη 2016 ποια σημεία βρήκατε και πως τα χαρακτηρίσατε;
Στο θέμα 3 της ίδιας εξεταστικής βρήκατε 1656*π/5;
Στο θέμα 5 βρήκατε 8sqrt(2)/3;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Singularity on September 10, 2017, 23:07:31 pm
Στο συνημμένο.
Στο θέμα 2 Σεπτέμβρη 2016 ποια σημεία βρήκατε και πως τα χαρακτηρίσατε;
Στο θέμα 3 της ίδιας εξεταστικής βρήκατε 1656*π/5;
Στο θέμα 5 βρήκατε 8sqrt(2)/3;
Στο θέμα 2 Σεπτέμβρη 2016 ποια σημεία βρήκατε και πως τα χαρακτηρίσατε;
Στο θέμα 3 της ίδιας εξεταστικής βρήκατε 1656*π/5;
Στο θέμα 5 βρήκατε 8sqrt(2)/3;
στο θέμα 5 σημφωνούμε
το θέμα 3 το βρήκα διαφορετικό όμως το ανεβάζω να το κοιταξεις να δούμε ποιο είναι το σωστό
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Apostolof on September 10, 2017, 23:27:37 pm
στο θέμα 5 σημφωνούμε
το θέμα 3 το βρήκα διαφορετικό όμως το ανεβάζω να το κοιταξεις να δούμε ποιο είναι το σωστό
το θέμα 3 το βρήκα διαφορετικό όμως το ανεβάζω να το κοιταξεις να δούμε ποιο είναι το σωστό
Ολοκλήρωνα στη σφαίρα x^2+(y-1)^2+z=9 :o
Που τη βρήκα ένας θεός ξέρει, μάλλον έβλεπα τα μισά από αυτό το θέμα και τα άλλα μισά από άλλο :D
Η δική σου λύση μου φαίνεται σωστή εκτός από ένα σημείο. Νομίζω μετά την αλλαγή του συστήματος το κέντρο της σφαίρας είναι στο O(0,0,0), δηλαδή το σχήμα δεν είναι σωστό. Για αυτό το λόγο και τα όρια του φ είναι από 0 έως π και όχι π/2. Άρα το νούμερο βγαίνει διπλάσιο.
Στο θέμα 2 βρήκες τα σημεία (0,0,1)(0,0,-1)(1,1,1)(1,1-1);
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nlazaridi on June 13, 2018, 17:26:48 pm
Εχει λυσει καποιος το θεμα 6 απο σεπτεμβριο 16?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Singularity on June 13, 2018, 18:00:17 pm
Εχει λυσει καποιος το θεμα 6 απο σεπτεμβριο 16?
ωραίο τρικάκι ο ατρέας βλέπω σε αυτή τη άσκηση, η λύση είναι σαν το θέμα 5β Ιουνίου 2015 που έχω ανεβασμένη στα downloads στο αρχείο με τα σοσ θέματα. Η μόνη διαφορά που έπρεπε να πεις είναι ότι στο ασυμπίεστο πεδίο G το ανόμαλο σημείο είναι εκτος των ορίων της σφαίρας που σου ζητούσε να βρεις τη ροή άρα η ροή που δημιουργεί το πεδίο αυτό θα είναι 0 (όσο πεδίο μπαίνει μέσα τόσο βγαίνει) (Flashback απο πεδίο 1 τώρα....). ελπίζω να σε κάλυψα, αντε τώρα να κοιοτάξω και τα δικά μου μαθήματα γιατί δεν θα περάσουμε τίποτα
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: geogrgepanag on June 16, 2018, 22:26:10 pm
Σεπτεμβριο 17 θεμα 4 καμια βοηθεια? Θελουμε 2 σχεσεις λογικα, η μια βγαινει απο την τιμη του εργου που δινεται.
Το οτι ειναι συντηρητικο σημαινει οτι το ολοκληρωμα της αποκλισης θα ειναι ισο με F(A)-F(B) ?
ή θεωρουμε δεδομενο οτι ειναι και αστροβιλο (δηλ περιστροφη=0)?
Το οτι ειναι συντηρητικο σημαινει οτι το ολοκληρωμα της αποκλισης θα ειναι ισο με F(A)-F(B) ?
ή θεωρουμε δεδομενο οτι ειναι και αστροβιλο (δηλ περιστροφη=0)?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Singularity on June 17, 2018, 00:02:31 am
το δεύτερο, κανε ολα τα εξωτερικά γινόμενα και στη κ συνιστώσα θα σου βγεί η σχέση. Βγαίνει και με το να πάρεις την εξίσωση λαπλας γιατί ολα τα πεδία που ασχολούμαστε στο λογισμό 2 ειναι συντηρητικά αλλα δεν είναι απόλυτα σωστo γιατι δεν σου το έδωσε η άσκηση σαν δεδομένο.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: katerinap99 on June 20, 2018, 12:57:46 pm
Σχετικο με τα προχθεσινα θεματα:
Για τον χαρακτηρισμο στασιμων σημειων,αν βρισκεις θετικες αλλα και μηδενικες ιδιοτιμες στον εσσιανο θεωρειται μικτα προσημασμενος;
Για τον χαρακτηρισμο στασιμων σημειων,αν βρισκεις θετικες αλλα και μηδενικες ιδιοτιμες στον εσσιανο θεωρειται μικτα προσημασμενος;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: The Audacious AI on June 20, 2018, 13:59:00 pm
Σχετικο με τα προχθεσινα θεματα:
Για τον χαρακτηρισμο στασιμων σημειων,αν βρισκεις θετικες αλλα και μηδενικες ιδιοτιμες στον εσσιανο θεωρειται μικτα προσημασμενος;
Για τον χαρακτηρισμο στασιμων σημειων,αν βρισκεις θετικες αλλα και μηδενικες ιδιοτιμες στον εσσιανο θεωρειται μικτα προσημασμενος;
http://prntscr.com/jx46bp
Η απάντηση στο ερώτημά σου από σημειώσεις Ατρέα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Argirios on September 07, 2018, 05:44:10 am
Όταν ζητάει να δείξουμε αν μία έκφραση είναι ολικό διαφορικό συνάρτησης, πρέπει να δείξουμε ότι ολοκληρώνεται η κάθε συνιστώσα μερικώς? πχ στο Σεπ 2016 θέμα 1
δλδ αμα ολοκληρωσουμε τις συνιστώσες ως προς χ,γ,ζ το αποτελεσμα να ειναι ιδιο για ολες και ισο με την f
δλδ αμα ολοκληρωσουμε τις συνιστώσες ως προς χ,γ,ζ το αποτελεσμα να ειναι ιδιο για ολες και ισο με την f
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Patui on September 07, 2018, 13:15:19 pm
Όταν ζητάει να δείξουμε αν μία έκφραση είναι ολικό διαφορικό συνάρτησης, πρέπει να δείξουμε ότι ολοκληρώνεται η κάθε συνιστώσα μερικώς? πχ στο Σεπ 2016 θέμα 1
δλδ αμα ολοκληρωσουμε τις συνιστώσες ως προς χ,γ,ζ το αποτελεσμα να ειναι ιδιο για ολες και ισο με την f
δλδ αμα ολοκληρωσουμε τις συνιστώσες ως προς χ,γ,ζ το αποτελεσμα να ειναι ιδιο για ολες και ισο με την f
Δες σημειώσεις Ατρέα , 2ο κεφάλαιο , σελίδα 46 στην αρχή. Εάν σου δίνει την έκφραση και θέλεις να τσεκάρεις εάν είναι ολικό διαφορικό , αρκεί να ικανοποιούνται οι σχέσεις που έχει . Εάν μετά σου ζητάει την συνάρτηση f μπορείς εύκολα με τον τύπο που έχει από κάτω ή κάνοντας αντιπαραγώγιση εάν είναι εύκολο για να γλιτώσεις τις πράξεις με το ολοκλήρωμα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Argirios on September 07, 2018, 21:12:13 pm
Δες σημειώσεις Ατρέα , 2ο κεφάλαιο , σελίδα 46 στην αρχή. Εάν σου δίνει την έκφραση και θέλεις να τσεκάρεις εάν είναι ολικό διαφορικό , αρκεί να ικανοποιούνται οι σχέσεις που έχει . Εάν μετά σου ζητάει την συνάρτηση f μπορείς εύκολα με τον τύπο που έχει από κάτω ή κάνοντας αντιπαραγώγιση εάν είναι εύκολο για να γλιτώσεις τις πράξεις με το ολοκλήρωμα.
θένχ γιου! ;)Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Σοκοφρέτας on September 09, 2018, 23:31:48 pm
Στα θέματα Ιουνίου του 2017 υπάρχουν ανεβασμένες απαντήσεις. Μπορεί κάποιος να μου πει αν υπάρχει κάποιο λάθος στην λύση του θέματος 3 (επισυνάπτω τη λύση που δίνεται). Το ερώτημα είναι να υπολογιστεί το συνολικό φορτίο επί του στερεού "τάδε" αν η πυκνότητα είναι ρ(x,y,z)= x^2 + y^2
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Amethyst on September 12, 2018, 15:04:34 pm
Στα θέματα Ιουνίου του 2017 υπάρχουν ανεβασμένες απαντήσεις. Μπορεί κάποιος να μου πει αν υπάρχει κάποιο λάθος στην λύση του θέματος 3 (επισυνάπτω τη λύση που δίνεται). Το ερώτημα είναι να υπολογιστεί το συνολικό φορτίο επί του στερεού "τάδε" αν η πυκνότητα είναι ρ(x,y,z)= x^2 + y^2
Όχι δεν υπάρχει λάθος στην λύση που έχεις επισυνάψει. Με αυτήν την εκφώνηση και αυτήν την πυκνότητα η απάντηση βγαίνει
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xaotikos on January 31, 2019, 20:24:09 pm
Σεπτέμβρης 17 θέμα 1 α ερώτημα κάποιος;; τι κάνουμε εκεί;
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Singularity on January 31, 2019, 21:13:52 pm
Σεπτέμβρης 17 θέμα 1 α ερώτημα κάποιος;; τι κάνουμε εκεί;
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: xaotikos on January 31, 2019, 22:09:45 pm
Τόσο απλό τελικά. Θενξ!
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: estavrian on June 10, 2019, 18:22:15 pm
Γιατί όταν παίρνεις df/dx το dx δεν επιδρά και στις μερικές παραγώγους fx και fy και επιδρά μόνο στα dx dy ;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: reservoir dog on September 12, 2019, 02:07:04 am
Μπορεί κάποιος να πει ποσο βρήκες στο 4ο του 19?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: MajorTom on June 22, 2020, 01:21:52 am
Θέμα 3, Σεπτέμβρης του 19, μπορεί να μου πει κανένας πως λύνεται;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 22, 2020, 02:10:33 am
Θέμα 3, Σεπτέμβρης του 19, μπορεί να μου πει κανένας πως λύνεται;
Ίσως κάπως έτσι
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 22, 2020, 15:22:35 pm
Ίσως κάπως έτσι
Βασικά ήταν αρκετά λάθος αυτό που έστειλα. Έτυχε να πέσω σε αυτήν την ερώτησ (https://math.stackexchange.com/questions/1090988/find-the-volume-of-the-region-of-a-sphere-bounded-by-two-planes), οπότε το ξαναπροσπάθησα... Σόρρυ για πριν :-[
Aν και ίσως να υπάρχει και πιο εύκολος τρόπος...
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: chrimalo on June 22, 2020, 17:50:30 pm
Γινεται καποιος να εξηγήσει πως το ρdρ μετατρέπεται ετσι οπως δειχνει η ασκηση; (ειναι απο τα διπλα ολοκλη.)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 22, 2020, 18:01:37 pm
Γινεται καποιος να εξηγήσει πως το ρdρ μετατρέπεται ετσι οπως δειχνει η ασκηση; (ειναι απο τα διπλα ολοκλη.)
παίρνεις τον τύπο αλλαγής συντεταγμένων, Κεφάλαιο 4, σελίδα 115 σημειώσεις Ατρέα. Απο όσο ξέρω επίσης δεν χρειάζεται να το αποδείξεις αν πρόκειται να το χρησιμοποιήσεις στις εξετάσεις
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: chrimalo on June 22, 2020, 18:10:34 pm
την πρωτη μετατροπη του dxdy σε ρdρdθ την εχω καταλαβει. Για να προκυψει το d((R^2-ρ^2)/2) χρειαζεται να κανω τον τροπο της οριζουσας αλλα με αντι για x και y να βαλω ρ θ;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 22, 2020, 19:16:05 pm
την πρωτη μετατροπη του dxdy σε ρdρdθ την εχω καταλαβει. Για να προκυψει το d((R^2-ρ^2)/2) χρειαζεται να κανω τον τροπο της οριζουσας αλλα με αντι για x και y να βαλω ρ θ;
αα σε εκείνο το σημείο δεν κάνει αλλαγή συστήματος συντεταγμένων, κάνει ένα "κολπάκι" με το διαφορικό για να βγεί πιο προφανής η ολοκλήρωση, αλλά είναι ακριβώς το ίδιο με τον προσπαθείς να λύσεις το
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: migk on June 23, 2020, 11:01:22 am
καλημέρα!
Θέμα 5 Ιουνίου 2019 (Α)
Στην τελευταία σχέση (pic) θέλει + ή - λόγω της φοράς διαγραφής που αλλαζει στο δεύτερο ολοκλήρωμα ?
Θέμα 5 Ιουνίου 2019 (Α)
Στην τελευταία σχέση (pic) θέλει + ή - λόγω της φοράς διαγραφής που αλλαζει στο δεύτερο ολοκλήρωμα ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nilatos on June 23, 2020, 11:10:20 am
Καλημέρα.
Νομίζω ότι ειναι "+".
Ρίξε μια ματία στο 4ο κεφάλαιο του Ατρέα σελ 109.
Νομίζω ότι ειναι "+".
Ρίξε μια ματία στο 4ο κεφάλαιο του Ατρέα σελ 109.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: migk on June 23, 2020, 17:09:09 pm
Καλημέρα.
Νομίζω ότι ειναι "+".
Ρίξε μια ματία στο 4ο κεφάλαιο του Ατρέα σελ 109.
Νομίζω ότι ειναι "+".
Ρίξε μια ματία στο 4ο κεφάλαιο του Ατρέα σελ 109.
Ευχαριστώ για τη απάντηση, δεν βρίσκω αυτές τις σημειώσεις που λες έχεις κάποιο link ? Σε ερώτηση που έκανα στο Mathematics Stack Exchange απάντησαν ότι είναι το πρώτο ολοκλήρωμα αρνητικό λόγω της φοράς και των ορίων ολοκλήρωσης. https://math.stackexchange.com/questions/3731230/find-the-work-oint-pdxqdy-of-the-fx-y-%e2%88%92y2-x2-on-the-rectangle-x%e2%88%92y-0/3731243#3731243 (https://math.stackexchange.com/questions/3731230/find-the-work-oint-pdxqdy-of-the-fx-y-%e2%88%92y2-x2-on-the-rectangle-x%e2%88%92y-0/3731243#3731243)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: vasilizaitsef on June 23, 2020, 20:17:41 pm
αφελής ερώτηση αλλά θα ήθελα να ακούσω την άποψη σας, πιστευετε τα θέματα θα κινηθούν στη λογική της δοκιμαστικής εξέτασης ή σε μια μίξη παλεών θεμάτων που έχουμε δώσει??
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 23, 2020, 21:54:23 pm
Ευχαριστώ για τη απάντηση, δεν βρίσκω αυτές τις σημειώσεις που λες έχεις κάποιο link ? Σε ερώτηση που έκανα στο Mathematics Stack Exchange απάντησαν ότι είναι το πρώτο ολοκλήρωμα αρνητικό λόγω της φοράς και των ορίων ολοκλήρωσης. https://math.stackexchange.com/questions/3731230/find-the-work-oint-pdxqdy-of-the-fx-y-%e2%88%92y2-x2-on-the-rectangle-x%e2%88%92y-0/3731243#3731243 (https://math.stackexchange.com/questions/3731230/find-the-work-oint-pdxqdy-of-the-fx-y-%e2%88%92y2-x2-on-the-rectangle-x%e2%88%92y-0/3731243#3731243)
Μια άλλη ιδέα ίσως θα ηταν αλλαγή συστήματος συντεταγμένων, έτσι ώστε να μετατοπίσεις το τετράγωνο κατάλληλα και να προέκυπτε ένα διπλό ολοκλήρωμα χωρίς να υπάρχει η ανάγκη να το σπάσεις σε δύο χωριά και θα είχε και εύκολα όρια σταθερά. Αν και από άποψη χρόνου ίσως να μην γλίτωνε και πολύ χρόνο...
αφελής ερώτηση αλλά θα ήθελα να ακούσω την άποψη σας, πιστευετε τα θέματα θα κινηθούν στη λογική της δοκιμαστικής εξέτασης ή σε μια μίξη παλεών θεμάτων που έχουμε δώσει??
Να πω την αλήθεια και εγώ το έχω απορία...
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: nilatos on June 23, 2020, 22:48:16 pm
Σελ 109,στο τέλος...ίσως είναι και μείον απλά είδα αυτό που λέει εκεί:
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 25, 2020, 17:03:29 pm
Νομίζω απο τις λίγες φορές που δεν μπήκε ούτε ένα θεώρημα φέτος :o
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: acapulco on June 25, 2020, 19:11:46 pm
ευκολα?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Condoriano on June 25, 2020, 20:47:03 pm
ευκολα?
Προσωπικά οχι δεν τα βρήκα εύκολα, είχαν πολλές πράξεις και αρκετή δουλεια. Ίσα ίσα τα θεωρήματα σου γλιτώνουν χρόνο πιστεύω και είναι πιο σύντομες οι απαντήσεις ....
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Cobb on June 25, 2020, 21:29:05 pm
Δεν νομίζω ότι ως προς την δυσκολία ήταν απαιτητικά, ιδιαίτερα του Ζάχαρη θεωρώ ότι ήταν αρκετά εύκολα και ο χρόνος υπεραρκετός. Συμφωνώ και εγώ, όμως, στο ότι τα θέματα του Ατρέα ήταν χρονοβόρα (αρκετές αριθμητικές πράξεις και δουλειά) και δεν μπορούσες να χρησιμοποιήσεις κανένα θεώρημα οπότε στένευαν πολύ τα χρονικά περιθώρια.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: illuv4tar on January 06, 2021, 20:43:34 pm
Στο 3ο ερωτημα 1ο θεμα απο Ζαχαρη τον Σεπτεμβρη μπορει να βοηθησει λιγο κανεις ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Evenina on January 06, 2021, 22:38:41 pm
Στο 3ο ερωτημα 1ο θεμα απο Ζαχαρη τον Σεπτεμβρη μπορει να βοηθησει λιγο κανεις ?
Αν εννοείς του 2020:
Για να βρεις τον ρυθμό μεταβολής παίρνεις την μερική παράγωγο ως προς την κατεύθυνση του α. Επειδή όμως η f είναι διαφορίσιμη, αυτό είναι ίσο με f'(x,y) * α. Το f'(x,y) είναι ίσο με το gradient της f, δηλαδή f'(x,y) = (fx, fy). Βρίσκεις τα fx, fy, πολλαπλασιάζεις με το α που έχεις βρει από το 2ο ερώτημα και τελείωσες ^.^
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: illuv4tar on January 30, 2021, 18:22:13 pm
Στα Θέματα Ατρέα Σεπτεμβρη , Θέμα 1ο, μπορει κανεις να βοηθησει λιγο με τις παραμετροποιήσεις και τα χωρια ?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: DIMITRIS2000 on May 25, 2022, 03:30:31 am
Στα Θέματα Ατρέα Σεπτεμβρη , Θέμα 1ο, μπορει κανεις να βοηθησει λιγο με τις παραμετροποιήσεις και τα χωρια ?
+1Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vagiatsan on June 21, 2022, 12:57:16 pm
Καλησπέρα παιδιά! Έχει κάποιος τις λύσεις απο τα θέματα του Φεβρουαρίου 2022;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Nikos_313 on June 21, 2022, 18:55:08 pm
Καλησπέρα παιδιά! Έχει κάποιος τις λύσεις απο τα θέματα του Φεβρουαρίου 2022;
Καλησπέρα,
έκατσα και τα έλυσα τα θέματα. Τώρα δεν ξέρω αν είναι σωστά αριθμητικά κτλ αλλά το σημαντικό είναι η μεθοδολογία για κάθε άσκηση...
(Δεν είμαι σίγουρος για το θέμα 2 και θέμα 5 - αν είναι κάτι λάθος στείλετε μου PM)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Local Rider on June 26, 2022, 23:27:04 pm
σεπτ 19 λύσεις;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Nikos_313 on June 27, 2022, 15:46:55 pm
σεπτ 19 λύσεις;
εδώ (κι άμα τώρα είναι αργά) :(Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Lincoln on August 26, 2022, 22:52:04 pm
Μπορεί κανείς να με βοηθήσει σε αυτήν;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Mr Watson on August 27, 2022, 00:11:27 am
Δεν θυμάμαι πώς ακριβώς λύνεται αλλά υπάρχει συγκεκριμένη μεθολογια. Έψαξες στις παραδόσεις του Ζάχαρη;
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Lincoln on August 27, 2022, 00:29:35 am
Ναι έψαξα και βρήκα την μεθοδολογία ωστόσο είμαι πολύ άσχετος ακόμα ώστε να βγάλω άκρη με το πως εφαρμόζεται. Ξεκίνησα να διαβάζω αυτές τις μέρες μετα από 2 χρόνια off με την σχολή. Χρωστάω 22μαθήματα και πρακτικά τώρα ξεκινάω να ασχολούμε. Πρώτο μάθημα που θα δώσω είναι ο λογισμός. Σόρρυ αν κουράζω αλλά μου φαίεται βουνό η όλη φάση και πρέπει κάπως να βγάλω άκρη
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Mr Watson on August 27, 2022, 02:00:18 am
Βρήκες την μεθοδολογία, είδες όμως την λύση του Ζάχαρη;
Την επισυνάπτω από κάτω. Αν δεν καταλαβαίνεις να προσπαθήσω να σου εξηγήσω
Την επισυνάπτω από κάτω. Αν δεν καταλαβαίνεις να προσπαθήσω να σου εξηγήσω
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Lincoln on August 27, 2022, 11:01:41 am
Την είδα την λύση Watson και την κατάλαβα (πρακτικά) ωστόσο στο πρόβλημα το επόμενο έχει λίγο διαφορετικό σύστημα και κόλλησα.
Ξεκινάω τώρα να δω όλες τις διαλέξεις και παράλληλα να λύνω και από κάτι. Πιστεύω θα με βοηθήσουν. Τι λες;
Ξεκινάω τώρα να δω όλες τις διαλέξεις και παράλληλα να λύνω και από κάτι. Πιστεύω θα με βοηθήσουν. Τι λες;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Caterpillar on August 27, 2022, 12:13:32 pm
Την είδα την λύση Watson και την κατάλαβα (πρακτικά) ωστόσο στο πρόβλημα το επόμενο έχει λίγο διαφορετικό σύστημα και κόλλησα.
Ξεκινάω τώρα να δω όλες τις διαλέξεις και παράλληλα να λύνω και από κάτι. Πιστεύω θα με βοηθήσουν. Τι λες;
Ναι δες αυτά που έχουν κάνει στα μαθήματα, αλλιώς δύσκολα να μπεις στο πνεύμα. Ξεκινάω τώρα να δω όλες τις διαλέξεις και παράλληλα να λύνω και από κάτι. Πιστεύω θα με βοηθήσουν. Τι λες;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Mr Watson on August 27, 2022, 13:00:23 pm
Η επόμενη άσκηση είναι διαφορετική. Ζητάει γενικά τα στάσιμα σημεία της f και όχι τα στάσιμα της f πάνω σε ορισμένη καμπύλη, όπως η άσκηση που έστειλες.
Συμφωνώ με το να το πιάσεις απ την αρχή. Είναι σημαντικό μάθημα, θα το βρίσκεις μπροστά σου και χρειάζεται να το νιώσεις. Θα το θυμηθείς κυρίως στα πεδία.
Συμφωνώ με το να το πιάσεις απ την αρχή. Είναι σημαντικό μάθημα, θα το βρίσκεις μπροστά σου και χρειάζεται να το νιώσεις. Θα το θυμηθείς κυρίως στα πεδία.
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: georkala on December 23, 2022, 13:12:41 pm
Υπάρχει λύση του θέματος 3 του Σεπτεμβρίου 2022?
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίε&#
Post by: alex_g on December 25, 2022, 15:39:58 pm
Επισυνάπτω τα αρχεία με τη λύση. Νομίζω πως είναι σωστά αλλά ας επιβεβαιώσει και κάποιος αν του είναι εύκολο. Η λογική της άσκησης αυτή είναι πάντως. Επίσης, το εμβαδόν στο τέλος μου βγήκε αρνητικό, οπότε παίρνεις την απόλυτη τιμή για να είσαι σωστός.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Vagiatsan on January 17, 2023, 00:39:29 am
Καλησπέρα παιδιά! Μήπως έχει κανείς τις λύσεις του Σεπτέμβρη 2022;;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: psaxno on May 28, 2023, 19:22:26 pm
Καλησπέρα σε όλους! Έχω μια ερώτηση για την άσκηση 3 του 06/2022 (είτε στην Α', είτε στη Β' ομάδα). Υπάρχει η λύση για την Β' ομάδα στα downloads, αλλά δεν καταλαβαίνω τη λογική. Ολοκληρώνουμε σε ένα χωρίο μεταξύ δύο ελλείψεων, και άρα μετατρέπουμε τα x και y σε πολικές συντεταγμένες. Δε θα έχουμε όμως άλλη μετατροπή για την "μικρή" έλλειψη και άλλη για την "μεγάλη"; Και μετά η ακτίνα ρ δε θα έχει όρια συναρτήσει της γωνίας θ, αφού πρόκειται για έλλειψη; Στη λύση δίνει σταθερά όρια από 1 έως 3. Γιατί όμως να μην βάζαμε για παράδειγμα από 1/3 έως 3. Αν μπορεί κάποιος να μου εξηγήσει λίγο, γιατί δεν βρίσκω και κάποια παρόμοια άσκηση σε αυτές του Ατρέα ή των βιβλίων του Ευδόξου.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Don on May 28, 2023, 19:37:27 pm
Καλησπέρα σε όλους! Έχω μια ερώτηση για την άσκηση 3 του 06/2022 (είτε στην Α', είτε στη Β' ομάδα). Υπάρχει η λύση για την Β' ομάδα στα downloads, αλλά δεν καταλαβαίνω τη λογική. Ολοκληρώνουμε σε ένα χωρίο μεταξύ δύο ελλείψεων, και άρα μετατρέπουμε τα x και y σε πολικές συντεταγμένες. Δε θα έχουμε όμως άλλη μετατροπή για την "μικρή" έλλειψη και άλλη για την "μεγάλη"; Και μετά η ακτίνα ρ δε θα έχει όρια συναρτήσει της γωνίας θ, αφού πρόκειται για έλλειψη; Στη λύση δίνει σταθερά όρια από 1 έως 3. Γιατί όμως να μην βάζαμε για παράδειγμα από 1/3 έως 3. Αν μπορεί κάποιος να μου εξηγήσει λίγο, γιατί δεν βρίσκω και κάποια παρόμοια άσκηση σε αυτές του Ατρέα ή των βιβλίων του Ευδόξου.
Εφόσον δεν ολοκληρώνεις παραμετροποιημένη συνάρτηση ρ(θ) δεν παίζει κανένα ρόλο, το σύστημα συντεταγμένων "τα αναλαμβάνει όλα" για σένα, και εφόσον κάνεις σωστά τη μετατροπή του συστήματος δεν έχεις κάποιο πρόβλημα.
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: Limpolits on August 19, 2023, 17:25:22 pm
Σημειώσεις Ατρέα, Κεφάλαιο 4, Λυμένη Άσκηση 3
Γιατί άμα αλλάξουμε τη σειρά ολοκλήρωσης (πρώτα ολοκλήρωση ως προς dx) κρατώντας τα όρια σταθερά, δεν προκύπτει το ίδιο αποτέλεσμα όπως θα πρέπε σύμφωνα με το θεώρημα 4.3;
Γιατί άμα αλλάξουμε τη σειρά ολοκλήρωσης (πρώτα ολοκλήρωση ως προς dx) κρατώντας τα όρια σταθερά, δεν προκύπτει το ίδιο αποτέλεσμα όπως θα πρέπε σύμφωνα με το θεώρημα 4.3;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: tzortzis on August 19, 2023, 17:44:21 pm
μηπως ξεχασες να λυσεις τις καμπυλες ως προς προς x, γιατι πλεον θα εχεις αλλα ορια ολοκληρωσεις, δεν θα τα κρατησεις τα ιδια, τις οριακες καμπυλες πρεπει να τις φερεις σε μορφη συναρτησης f(y) και μετα απο αυτο, κατα την ολοκληρωση κατα dy να βαλεις τους σταθερους αριθμους αναλογα με το απο που εως που παει το y
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: thenoface on September 08, 2024, 16:22:06 pm
εχουμε λυσεισ για ιουνιο του 22 το θεμα 2 και σεμπτεβριο του 23 θεμα 2;
Title: Re: [Λογισμός ΙΙ] Παλιά θέματα, Σχολιασμός και απορίες
Post by: el mariachi on January 22, 2025, 16:42:28 pm
εγω θα αφησω εδω τις συγκεκριμενες διαλεξεις https://www.youtube.com/watch?v=tGVnBAHLApA&list=PLDesaqWTN6ESk16YRmzuJ8f6-rnuy0Ry7&index=1 οι οποιες ειναι ολα οσα πρεπει να ξερετε για τον λογισμο 2. τα πιανει απο την αρχη. διανυσματα, επιπεδα, επιφανειες, καμπυλες, ολοκληρωματα, παραγωγοι κλπ κλπ. εχει πολλα παραδειγματα και εχει ειδικα στην αρχη βασικα πραγματα οπως πως να σχεδιαζεις τα γραφηματα στον R3 κατι που ειναι σημαντικο για να λυσεις ολοκληρωματα. αν δειτε τις διαλεξεις, διαβασετε και τις σημειωσεις των καθηγητων και λυσετε και τις ασκησεις των σημειωσεων, τοτε θα ειστε κομπλε. υπαρχουν καποια βιντεο που δεν χρειαζεται να δειτε, αλλα ποια ειναι αυτα θα τα καταλαβετε στην πορεια. οι διαλεξεις ειναι ευχαριστες και δεν κουραζουν καθολου. κατ εμε ειναι οτι πρεπει για να περασεις το μαθημα και να κατανοησεις τις εννοιες