Title: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on February 17, 2019, 21:22:38 pm
Για οποιαδήποτε απορία πάνω στις ασκήσεις.
Για απορίες στα παλιά θέματα στο αντίστοιχο τόπικ (https://www.thmmy.gr/smf/index.php?topic=32998.0). Stay on topic!
Για απορίες στα παλιά θέματα στο αντίστοιχο τόπικ (https://www.thmmy.gr/smf/index.php?topic=32998.0). Stay on topic!
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ctsompos on May 27, 2019, 18:26:55 pm
Στη γραμμική ανάδραση καταστάσεων πώς υπολογίζουμε το kr με πίνακες στον παρανομαστή ?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: TheoProt on May 27, 2019, 20:38:23 pm
Στη γραμμική ανάδραση καταστάσεων πώς υπολογίζουμε το kr με πίνακες στον παρανομαστή ?
Υπάρχει ο τύπος υπολογισμού στις σημειώσεις του Ροβιθάκη που είναι ανεβασμένες στο elearning. k r = −1 / C*(A − B*K)-1*B
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Φασολάκια με Πρόβειο on May 27, 2019, 21:10:56 pm
Στη γραμμική ανάδραση καταστάσεων πώς υπολογίζουμε το kr με πίνακες στον παρανομαστή ?
Επίσης επειδή αναφέρεις τον παρονομαστή, οι πίνακες καταλήγουν μετά από πράξεις σε βαθμωτό μέγεθος αν εννοείς αυτό.Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ctsompos on May 27, 2019, 21:23:49 pm
Επίσης επειδή αναφέρεις τον παρονομαστή, οι πίνακες καταλήγουν μετά από πράξεις σε βαθμωτό μέγεθος αν εννοείς αυτό.
ναι αυτό εννοω αν και δε μπορώ να καταλάβω πως θα καταλήξουν οι πίνακες σε σταθερό αλλά λογικά θα υπάρχει κάπου κάνα λυμένο παράδειγμα ;D Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: TheoProt on May 27, 2019, 21:28:45 pm
ναι αυτό εννοω αν και δε μπορώ να καταλάβω πως θα καταλήξουν οι πίνακες σε σταθερό αλλά λογικά θα υπάρχει κάπου κάνα λυμένο παράδειγμα ;D
Απλά με τις πράξεις μεταξύ των πινάκων, καταλήγεις σε βαθμωτό μέγεθος. Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: VforVoltage on May 27, 2019, 21:34:18 pm
Επίσης επειδή αναφέρεις τον παρονομαστή, οι πίνακες καταλήγουν μετά από πράξεις σε βαθμωτό μέγεθος αν εννοείς αυτό.
ωραίος, αλλιώς ο θείος Ρόβι θα βάλει ένα προζυμένιο κουλούρι και θα πρέπει να ελαχιστοποιήσουμε την παρουσία μας δίπλα του μετά από αυτό
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Φασολάκια με Πρόβειο on May 27, 2019, 21:59:23 pm
Ίσως και να είναι η ιδέα μου αλλά διακρίνω έτσι μια διαβολική ευχαρίστηση να μηδενιζει πράγματα
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: babyshark on May 27, 2019, 22:08:15 pm
Ίσως και να είναι η ιδέα μου αλλά διακρίνω έτσι μια διαβολική ευχαρίστηση να μηδενιζει πράγματα
^hello^ ^hello^ ^hello^ ^hello^ ^hello^
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: MrRobot on May 27, 2019, 23:02:02 pm
ναι αυτό εννοω αν και δε μπορώ να καταλάβω πως θα καταλήξουν οι πίνακες σε σταθερό αλλά λογικά θα υπάρχει κάπου κάνα λυμένο παράδειγμα ;D
Δες τις διαστάσεις των πινάκων. To διάνυσμα C έχει μέγεθος [1 επι 2]. Ο πίνακας (A - BK) είναι [2 επί 2] και το Β είναι [2 επί 1]. Αν τα πολλαπλασιάσεις όλα αυτά προκύπτει διάνυσμα μεγέθους [1 επί 1], δηλαδή βαθμωτό μέγεθος.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: spoun on June 06, 2019, 00:43:29 am
Πώς δείχνουμε ότι ένα σύστημα είναι σταθεροποιήσιμο ;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: spoun on June 06, 2019, 01:04:23 am
Επίσης πώς επιλέγουμε πίνακα μετασχηματισμού T ;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: MrRobot on June 06, 2019, 01:23:06 am
Σταθεροποιησιμο είναι ένα σύστημα του οποίου μπορούμε να ελέγξουμε τις ασταθείς ιδιοτιμές. Σε κάποιο σημείο των μαθημάτων ο ροβι λέει ότι κάθε σύστημα σπάει σε ένα ελεγξιμο και ένα μη ελεγξιμο. Αν το μη ελεγξιμο έχει έστω και μία μη ευσταθη ιδιοτιμη τότε το σύστημα είναι μη σταθεροποιησιμο.
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Patatompataria on June 06, 2019, 01:30:23 am
Επίσης πώς επιλέγουμε πίνακα μετασχηματισμού T ;
αναλόγως νομίζω σε τι θες να το μετασχηματίσεις. Αν πχ θες να το πας σε ελέγξιμη κανονική μορφή, τότε T = (M κυματιστό) * M-1, δες αναλυτικά την ενότητα 5.3 σελ. 62-63 στις σημειώσεις του kongr45gpen
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: spoun on June 06, 2019, 02:02:49 am
αναλόγως νομίζω σε τι θες να το μετασχηματίσεις.
Αν πχ θες να το πας σε ελέγξιμη κανονική μορφή, τότε T = (M κυματιστό) * M-1, δες αναλυτικά την ενότητα 5.3 σελ. 62-63 στις σημειώσεις του kongr45gpen
Αν πχ θες να το πας σε ελέγξιμη κανονική μορφή, τότε T = (M κυματιστό) * M-1, δες αναλυτικά την ενότητα 5.3 σελ. 62-63 στις σημειώσεις του kongr45gpen
Οι σημειώσεις αυτές βρίσκονται στα Downloads;
Δεν μπορώ να τις βρώ
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Patatompataria on June 06, 2019, 12:59:00 pm
http://helit.org/ece-notes/sae2.pdf
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on June 07, 2019, 10:41:53 am
Καποιος που να έχει καμιά ιδέα τι σημαίνει απόλυτη τιμή ενος πίνακα (πχ |Α|), είναι ή νόρμα του ? Και αν ναί πια απο τίς νορμες του ?
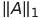 ή
ή 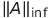
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mermaid on June 07, 2019, 19:09:35 pm
Οταν μας ζηταει ελεγκτη γραμμικής ανάδρασης καταστάσεων, το kr*r το συμπεριλαμβάνω μονο οταν μου διευκρινίζει οτι θελει η εξοδος να συγκλίνει σε μια τιμη; :???:
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Patatompataria on June 07, 2019, 20:05:16 pm
Καποιος που να έχει καμιά ιδέα τι σημαίνει απόλυτη τιμή ενος πίνακα (πχ |Α|), είναι ή νόρμα του ? Και αν ναί πια απο τίς νορμες του ?
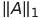 ή
ή 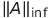
αρκετές φορές εννοεί την ορίζουσα
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on June 07, 2019, 20:16:16 pm
αρκετές φορές εννοεί την ορίζουσα
Δεν είναι ξεκάθαρο τι εννοεί ομως. Θα μπορούσε είτε να είναι η πρωτη νορμα ||A||1 είτε η δευτερη νόρμα ||A||2 είτε η ορίζουσα. Υπάρχει κάποιος τρόπος να ξέρουμε σε κάθε περίπτωση τί εννοεί ; :D
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 07, 2019, 20:57:35 pm
http://prntscr.com/nyz18s
http://prntscr.com/nyz1g8
Από ότι καταλαβαίνω στα γραμμικα συστηματα μπορουμε απο την ευσταθεια του ΣΙ να βγαλουμε συμπερασμα για την ευσταθεια ολου του συστηματος. Ομως εδω ο ροβι λεει οτι οταν οι ιδιοτιμες ειναι αποκλειστικα αριστερα και μονο
α) το ΣΙ ειναι εκθετικα ευσταθες
β) το συστημα ειναι ασυμπτωτικα ευσταθες
οποτε τι απο τα 2 ειναι το συστημα. My guess: η εκθετικη ευσταθεια αναφερεται καθαρα και μονο στην περιπτωση που το συστημα εχει πινακα Α διαγωνιο (η εστω block διαγωνιο)
http://prntscr.com/nyz1g8
Από ότι καταλαβαίνω στα γραμμικα συστηματα μπορουμε απο την ευσταθεια του ΣΙ να βγαλουμε συμπερασμα για την ευσταθεια ολου του συστηματος. Ομως εδω ο ροβι λεει οτι οταν οι ιδιοτιμες ειναι αποκλειστικα αριστερα και μονο
α) το ΣΙ ειναι εκθετικα ευσταθες
β) το συστημα ειναι ασυμπτωτικα ευσταθες
οποτε τι απο τα 2 ειναι το συστημα. My guess: η εκθετικη ευσταθεια αναφερεται καθαρα και μονο στην περιπτωση που το συστημα εχει πινακα Α διαγωνιο (η εστω block διαγωνιο)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: MrRobot on June 07, 2019, 21:14:09 pm
Γενικά η εκθετική ευστάθεια είναι μια πιο αυστηρή μορφή της ασυμπτωτικής ευστάθειας. Αποδεικνύεται και με άλλους τρόπους, αλλά για τα πλαίσια των ΣΑΕ ΙΙ νομίζω αρκεί αυτό που λες.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on June 07, 2019, 22:51:39 pm
Δεδομένου ότι μια σταθερά c>0 είναι άγνωστη θα μπορούσε να χρησιμοποιηθεί στην κατασκευή μιας συνάρτησης Lyapunov ?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: MrRobot on June 07, 2019, 23:02:33 pm
Μπορείς να πεις που το είδες;
Γενικά αν δεν χρησιμοποιείς κάπου την τιμή της, και σου αρκεί που είναι θετική πιστεύω πως ναι. Αλλά καλύτερα δώσε και ένα παράδειγμα.
Γενικά αν δεν χρησιμοποιείς κάπου την τιμή της, και σου αρκεί που είναι θετική πιστεύω πως ναι. Αλλά καλύτερα δώσε και ένα παράδειγμα.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on June 07, 2019, 23:20:29 pm
Μπορείς να πεις που το είδες;
Γενικά αν δεν χρησιμοποιείς κάπου την τιμή της, και σου αρκεί που είναι θετική πιστεύω πως ναι. Αλλά καλύτερα δώσε και ένα παράδειγμα.
Γενικά αν δεν χρησιμοποιείς κάπου την τιμή της, και σου αρκεί που είναι θετική πιστεύω πως ναι. Αλλά καλύτερα δώσε και ένα παράδειγμα.
Δεν θυμάμα να το είδα κάπου συγκεκριμένα :D . Απλά επειδή στους ελεγκτές ξέρω πως δεν επιτρέπεται σκέφτηκα πως ίσως να μην επιτρέπεται ούτε στις Lyapunov. Ευχαριστώ πάντως!
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: babyshark on June 08, 2019, 09:12:23 am
Οταν μας ζηταει ελεγκτη γραμμικής ανάδρασης καταστάσεων, το kr*r το συμπεριλαμβάνω μονο οταν μου διευκρινίζει οτι θελει η εξοδος να συγκλίνει σε μια τιμη; :???:
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiro on June 08, 2019, 11:13:02 am
Άπαξ και το σύστημα είναι ελέγξιμο, συνεπώς έχει νόημα να μιλώ για γραμμικό ελεγκτή ανάδρασης καταστάσεων, η έξοδος πάντα συγκλίνει σε τιμή. Αν δεν υπάρχει είσοδος αναφοράς τότε η έξοδος στη μόνιμη κατάσταση θα συγκλίνει στο 0, αν υπάρχει θέλεις και τον όρο kr*r ώστε να εξασφαλίσεις ότι y=r στη μόνιμη κατάσταση.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mermaid on June 08, 2019, 11:27:56 am
ως εισοδο αναφορας εννοεις την u;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on June 08, 2019, 12:48:10 pm
Παιδιά ποια είναι η διαφορά μεταξύ ενός τοπικά ασυμπτωτικα ευσταθους σημείου και ενός ολικά ασυμπτωτικα ευσταθους σημείου? Διάφορα ως προς τα κριτήρια που πρέπει να πληρούν..
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: chrispap4 on June 08, 2019, 13:23:17 pm
Θέλετε να κάνουμε discord το βράδυ για να συζητήσουμε λύσεις παλιών θεμάτων;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 08, 2019, 13:53:42 pm
Και γω το σκεφτηκα αλλα θα γινει λιγο μπουρδελο. Σαν εναλλακτικη ελεγα μηπως στηναμε ενα τσατρουμ με topics συγκεκριμενα δυσκολα θεματα συγκεκριμενων χρονων και να πεταξει ο καθενας την ιδεα του, την υλοποιηση του η οτιδηποτε μπορει να συνεισφερει ωστε να δημιουργησουμε λυσεις για καποια θεματα τα οποια δεν εχουν λυσεις.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Prison Mike on June 08, 2019, 13:54:48 pm
Παιδιά ποια είναι η διαφορά μεταξύ ενός τοπικά ασυμπτωτικα ευσταθους σημείου και ενός ολικά ασυμπτωτικα ευσταθους σημείου? Διάφορα ως προς τα κριτήρια που πρέπει να πληρούν..
Νομίζω χωρίς να έιμαι σίγουρος πως ολικά ασυμπτωτικά ευσταθές είναι το σημείο ισορροπίας σου αν και μόνο αν το πεδίο εφαρμογής του θεωρήματος Lyapunov είναι ολόκληρος ο χώρος καταστάσεων ( δηλαδή οι συναρτήσεις V(x), dV(x)/dt έχουν πεδίο εφαρμογής ολοκληρό το R^n και δεν περιορίζονται απο κάποιο κύκλο με ακτίνα ρ πχ Βr(0)={x ε R^2 : X1^2 + X2^2 < ρ ^2 }, οπου εδώ το πεδίο εφαρμογής του θεωρήματος Lyapunov σου είναι περιορισμένο)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mgavalet on June 08, 2019, 14:27:59 pm
Θέλετε να κάνουμε discord το βράδυ για να συζητήσουμε λύσεις παλιών θεμάτων;
ok καλη ιδεα
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on June 08, 2019, 14:33:34 pm
Νομίζω χωρίς να έιμαι σίγουρος πως ολικά ασυμπτωτικά ευσταθές είναι το σημείο ισορροπίας σου αν και μόνο αν το πεδίο εφαρμογής του θεωρήματος Lyapunov είναι ολόκληρος ο χώρος καταστάσεων ( δηλαδή οι συναρτήσεις V(x), dV(x)/dt έχουν πεδίο εφαρμογής ολοκληρό το R^n και δεν περιορίζονται απο κάποιο κύκλο με ακτίνα ρ πχ Βr(0)={x ε R^2 : X1^2 + X2^2 < ρ ^2 }, οπου εδώ το πεδίο εφαρμογής του θεωρήματος Lyapunov σου είναι περιορισμένο)
Σε ευχαριστώ πολύ!!
Σε ευχαριστώ πολύ!!
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 08, 2019, 15:48:27 pm
https://discord.gg/2ADgRY
Does it work?Οποιος μπει δινω δικαιωματα.
Does it work?Οποιος μπει δινω δικαιωματα.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 08, 2019, 16:27:59 pm
Αν εχω συστημα το οποιο περιεχει μια u. Το ΣΙ το βρισκω μηδενίζοντας την u ή συναρτησει της u? [δηλαδη (x1 *,x2 *,u *) = (0, x2 *, g(x2 * )) ]
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: babyshark on June 08, 2019, 16:28:23 pm
Εστω οτι μας δινεται ενα συστημα και αποδεικνυουμε οτι ειναι μη ελεγξιμο.Μπορουμε για αυτο το συστημα να σχεδιασουμε ελεγκτη αν κανουμε την κλασσικη διαδικασια με ελεγξιμο και μη ελεγξιμο μερος; δεν μπορω να καταλαβω :'( :'(
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiro on June 08, 2019, 17:13:20 pm
Αν εχω συστημα το οποιο περιεχει μια u. Το ΣΙ το βρισκω μηδενίζοντας την u ή συναρτησει της u? [δηλαδη (x1 *,x2 *,u *) = (0, x2 *, g(x2 * )) ]
To ΣΙ το βρίσκεις λύνοντας τις Fi(xi)=0, όπου Fi το δεξί μέλος των εξισώσεων xi παράγωγος=0. Αν από τη λύση αυτή σου προκύψει τιμή για το u συναρτήσει κάποιων MK που δεν είναι μηδενικές, τότε αυτό είναι το u*. Γενικά, με την υπόθεση ότι u ε R, ως ΣΙ ορίζεται ένα ζεύγος (x*,u*) ε R^(n+1) το οποίο ικανοποιεί το παραπάνω.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Florence on June 08, 2019, 17:36:55 pm
τοτε εδω γιατι ο ροβυ το εχει παρει ετσι? (απο τις σημειωσες του μαθηματος)
http://prntscr.com/nz90t5
http://prntscr.com/nz90t5
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiro on June 08, 2019, 17:45:33 pm
Εστω οτι μας δινεται ενα συστημα και αποδεικνυουμε οτι ειναι μη ελεγξιμο.Μπορουμε για αυτο το συστημα να σχεδιασουμε ελεγκτη αν κανουμε την κλασσικη διαδικασια με ελεγξιμο και μη ελεγξιμο μερος; δεν μπορω να καταλαβω :'( :'(
Ελεγκτή για οποιοδήποτε σύστημα υπάρχει μπορείς (θεωρητικά) να σχεδιάσεις. Το ζήτημα είναι το εξής: θα έχει θετική συνεισφορά στο να λύσω το πρόβλημα ή θα είναι άχρηστος;
Στο δια ταύτα. Έχεις εσύ ένα σύστημα το οποίο είναι μη ελέγξιμο. Αυτό τι σημαίνει; Πως όποιον γραμμικό ελεγκτή και να δοκιμάσεις, δεν θα καταφέρεις ποτέ να πας από μια αρχική κατάσταση στο 0 σε πεπερασμένο χρόνο. Το θεώρημα ύπαρξης μετασχηματισμού Τ τέτοιου ώστε το αρχικό σύστημα να μπορεί να σπάσει σε ένα ελέγξιμο και ένα μη-ελέγξιμο κομμάτι δεν σου κάνει ως δια μαγείας ελέγξιμο το σύστημα. Υπό προϋποθέσεις όμως στο κάνει σταθεροποιήσημο. Τι σημαίνει σταθεροποιήσιμο; Πως αν ξεκινήσω από μια αρχική κατάσταση ΟΚ δεν θα μπορέσω ποτέ να πάω στο 0, μπορώ όμως να καταφέρω να το πάω σε κάποια τιμή κάπου κοντά στο 0. Πόσο κοντά στο 0; Τόσο όσο μου επιτρέπουν οι ιδιοτιμές του πίνακα Α22 του μη-ελέγξιμου κομματιού.
Γιατί αυτό; Γιατί μετά τον μετασχηματισμό του αρχικού συστήματος, λαμβάνεις ένα σύστημα για τα z1,z2 παράγωγοι για το οποίο το θεώρημα σου λέει ότι σιγουρα το ζεύγος (Α11,Β11) θα είναι ελέγξιμο. Άρα έχει νόημα να πάρεις γραμμικό ελεγκτή ανάδρασης ώστε να μετακινήσεις τις ιδιοτιμές αυτού του ζεύγους τόσο αριστερά όσο επιθυμείς. Συνεπώς, και βάσει του ορισμού της ελεγξιμότητας, θα υπάρχει και ελεγκτής τέτοιος ώστε ξεκινώντας από μια αρχική τιμή z1(0) να μπορεί να σου το πάει το (Α11,Β11) στο 0 σε πεπερασμένο χρόνο. Έχεις όμως κι έναν έξτρα όρο ο οποίος είναι (κάτι σαν) διαταραχές. Αυτός ο όρος συμπεριλαμβάνει έναν πίνακα μετάβασης e^(A2τ). Αν ο πίνακας Α2 έχει ιδιοτιμές στα αριστερά, δηλ. είναι ευσταθής, τότε ΟΚ ίσως να μην είναι και ο πιο γρήγορος (αφού δεν μπορώ να τον ελέγξω με κάποιον τρόπο· η εξίσωση για το z2 παράγωγος δεν περιέχει όρο ελεγκτή), αλλά κάπου θα συγκλίνει.
edit: Προφανώς αν το σύστημα μου είναι ελέγξιμο εξαρχής, είναι και σταθεροποιήσιμο.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiro on June 08, 2019, 18:00:07 pm
τοτε εδω γιατι ο ροβυ το εχει παρει ετσι? (απο τις σημειωσες του μαθηματος)
http://prntscr.com/nz90t5
http://prntscr.com/nz90t5
Αποκλείεται να είπε τέτοιο πράγμα. Το πιο πιθανόν είναι να πήρε για ευκολία u=0 γιατί δεν είχε μιλήσει ακόμη για ελεγκτές τότε. Είναι λάθος αυτό που γράφει ο συνάδελφος στις σημειώσεις. Εξ' ορισμού, σημεία ισορροπίας είναι οι (οποιεσδήποτε) σταθερές λύσεις μιας διαφορικής εξίσωσης.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: babyshark on June 08, 2019, 18:05:57 pm
Ελεγκτή για οποιοδήποτε σύστημα υπάρχει μπορείς (θεωρητικά) να σχεδιάσεις. Το ζήτημα είναι το εξής: θα έχει θετική συνεισφορά στο να λύσω το πρόβλημα ή θα είναι άχρηστος;
Στο δια ταύτα. Έχεις εσύ ένα σύστημα το οποίο είναι μη ελέγξιμο. Αυτό τι σημαίνει; Πως όποιον γραμμικό ελεγκτή και να δοκιμάσεις, δεν θα καταφέρεις ποτέ να πας από μια αρχική κατάσταση στο 0 σε πεπερασμένο χρόνο. Το θεώρημα ύπαρξης μετασχηματισμού Τ τέτοιου ώστε το αρχικό σύστημα να μπορεί να σπάσει σε ένα ελέγξιμο και ένα μη-ελέγξιμο κομμάτι δεν σου κάνει ως δια μαγείας ελέγξιμο το σύστημα. Υπό προϋποθέσεις όμως στο κάνει σταθεροποιήσημο. Τι σημαίνει σταθεροποιήσιμο; Πως αν ξεκινήσω από μια αρχική κατάσταση ΟΚ δεν θα μπορέσω ποτέ να πάω στο 0, μπορώ όμως να καταφέρω να το πάω σε κάποια τιμή κάπου κοντά στο 0. Πόσο κοντά στο 0; Τόσο όσο μου επιτρέπουν οι ιδιοτιμές του πίνακα Α22 του μη-ελέγξιμου κομματιού.
Γιατί αυτό; Γιατί μετά τον μετασχηματισμό του αρχικού συστήματος, λαμβάνεις ένα σύστημα για τα z1,z2 παράγωγοι για το οποίο το θεώρημα σου λέει ότι σιγουρα το ζεύγος (Α11,Β11) θα είναι ελέγξιμο. Άρα έχει νόημα να πάρεις γραμμικό ελεγκτή ανάδρασης ώστε να μετακινήσεις τις ιδιοτιμές αυτού του ζεύγους τόσο αριστερά όσο επιθυμείς. Συνεπώς, και βάσει του ορισμού της ελεγξιμότητας, θα υπάρχει και ελεγκτής τέτοιος ώστε ξεκινώντας από μια αρχική τιμή z1(0) να μπορεί να σου το πάει το (Α11,Β11) στο 0 σε πεπερασμένο χρόνο. Έχεις όμως κι έναν έξτρα όρο ο οποίος είναι (κάτι σαν) διαταραχές. Αυτός ο όρος συμπεριλαμβάνει έναν πίνακα μετάβασης e^(A2τ). Αν ο πίνακας Α2 έχει ιδιοτιμές στα αριστερά, δηλ. είναι ευσταθής, τότε ΟΚ ίσως να μην είναι και ο πιο γρήγορος (αφού δεν μπορώ να τον ελέγξω με κάποιον τρόπο· η εξίσωση για το z2 παράγωγος δεν περιέχει όρο ελεγκτή), αλλά κάπου θα συγκλίνει.
Στο δια ταύτα. Έχεις εσύ ένα σύστημα το οποίο είναι μη ελέγξιμο. Αυτό τι σημαίνει; Πως όποιον γραμμικό ελεγκτή και να δοκιμάσεις, δεν θα καταφέρεις ποτέ να πας από μια αρχική κατάσταση στο 0 σε πεπερασμένο χρόνο. Το θεώρημα ύπαρξης μετασχηματισμού Τ τέτοιου ώστε το αρχικό σύστημα να μπορεί να σπάσει σε ένα ελέγξιμο και ένα μη-ελέγξιμο κομμάτι δεν σου κάνει ως δια μαγείας ελέγξιμο το σύστημα. Υπό προϋποθέσεις όμως στο κάνει σταθεροποιήσημο. Τι σημαίνει σταθεροποιήσιμο; Πως αν ξεκινήσω από μια αρχική κατάσταση ΟΚ δεν θα μπορέσω ποτέ να πάω στο 0, μπορώ όμως να καταφέρω να το πάω σε κάποια τιμή κάπου κοντά στο 0. Πόσο κοντά στο 0; Τόσο όσο μου επιτρέπουν οι ιδιοτιμές του πίνακα Α22 του μη-ελέγξιμου κομματιού.
Γιατί αυτό; Γιατί μετά τον μετασχηματισμό του αρχικού συστήματος, λαμβάνεις ένα σύστημα για τα z1,z2 παράγωγοι για το οποίο το θεώρημα σου λέει ότι σιγουρα το ζεύγος (Α11,Β11) θα είναι ελέγξιμο. Άρα έχει νόημα να πάρεις γραμμικό ελεγκτή ανάδρασης ώστε να μετακινήσεις τις ιδιοτιμές αυτού του ζεύγους τόσο αριστερά όσο επιθυμείς. Συνεπώς, και βάσει του ορισμού της ελεγξιμότητας, θα υπάρχει και ελεγκτής τέτοιος ώστε ξεκινώντας από μια αρχική τιμή z1(0) να μπορεί να σου το πάει το (Α11,Β11) στο 0 σε πεπερασμένο χρόνο. Έχεις όμως κι έναν έξτρα όρο ο οποίος είναι (κάτι σαν) διαταραχές. Αυτός ο όρος συμπεριλαμβάνει έναν πίνακα μετάβασης e^(A2τ). Αν ο πίνακας Α2 έχει ιδιοτιμές στα αριστερά, δηλ. είναι ευσταθής, τότε ΟΚ ίσως να μην είναι και ο πιο γρήγορος (αφού δεν μπορώ να τον ελέγξω με κάποιον τρόπο· η εξίσωση για το z2 παράγωγος δεν περιέχει όρο ελεγκτή), αλλά κάπου θα συγκλίνει.
ευχαριστω παρα πολυ,πληρως κατανοητο ;D ;D ;D
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Florence on June 08, 2019, 18:11:25 pm
Αποκλείεται να είπε τέτοιο πράγμα. Το πιο πιθανόν είναι να πήρε για ευκολία u=0 γιατί δεν είχε μιλήσει ακόμη για ελεγκτές τότε. Είναι λάθος αυτό που γράφει ο συνάδελφος στις σημειώσεις. Εξ' ορισμού, σημεία ισορροπίας είναι οι (οποιεσδήποτε) σταθερές λύσεις μιας διαφορικής εξίσωσης.
και στις δικες μου σημειωσεις το ιδιο εχω..αρα θα το ειπε..μπορει οντως να το πηρε για ευκολια..αλλα το πηρε
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 08, 2019, 18:14:55 pm
ετνομεταξυ οταν γραμμικοποιουμε ενα συστημα μεσω ελεγκτη u (γραμμικοποιηση μεσω αναδρασης) υπαρχει μια αντιφαση. γιατι για να εφαρμοσω ελεγκτη πρεπει να αποδειξω οτι ειναι ελεγξιμο (ασχετως του λογου του οποιου εφαρμοζω τον ελεγκτη, το εχει ξεκαθαρισει ο ροβι οτι πριν βαλεις οποιονδηποτε ελεγκτη πρεπει να εχουμε αποδειξει ελεγξιμοτητα) αλλα για να αποδειξω οτι ειναι ελεγξιμο πρεπει να παρω πινακες αρα να ειναι γραμμικο. συνεπως οταν εχουμε ασκησει με μη γραμμικο συστημα, το γραμμικοποιουμε μεσω αναδρασης (εφ οσων εχει ζητηθει προφανως) χωρις να εχουμε δειξει κατι για την ελεγξιμοτητα...
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: lnx on June 08, 2019, 18:52:21 pm
Η ελάχιστη υλοποίηση που ρωτάει σε κάποια θέματα(π.χ. 1ο Ιανουάριος 2019) τί είναι ;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on June 08, 2019, 18:59:23 pm
Η ελάχιστη υλοποίηση που ρωτάει σε κάποια θέματα(π.χ. 1ο Ιανουάριος 2019) τί είναι ;
να ειναι παρατηρησιμο και ελεγξιμο
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: spoun on June 08, 2019, 19:16:17 pm
να ειναι παρατηρησιμο και ελεγξιμο
Νομίζω ότι σε τέτοια ερωτήματα το ζητούμενο είναι ο πιο απλός ελεγκτής ( δηλαδή ένας ελεγκτής με τους ελάχιστους όρους, μπορείς να πεις ότι στις ασκήσεις κοιτάω να μηδενίσω κάποιο συντελεστή k για να διώξω όρους) με την προϋπόθεση ότι το σύστημα θα παραμείνει παρατηρήσιμο και ελέγξιμο.
Αυτό κατάλαβα εγώ, αν έχω λάθος ας με διορθώσει κάποιος.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on June 08, 2019, 19:54:35 pm
Σε ποια περίπτωση παίρνουμε δυναμική ανάδραση καταστάσεων ? (ελεγκτή με ολοκληρωτή)?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on June 08, 2019, 20:09:16 pm
Συστήματα ανοιχτού και κλειστού βροχου τι εννοεί?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Bojack Horseman on June 09, 2019, 17:08:44 pm
Όταν θέλω να φέρω το σύστημα στην κανονική ελέγξιμη μορφή, πρέπει να βρω τον πίνακα Τ για τον μετασχηματισμό z=Tx. Αυτός βρίσκεται μέσω του τύπου: Τ = M_bar*M^(-1). Για να βρω το M_bar όμως, χρειάζομαι το B_bar. Αλλά το B_bar προκύπτει μόνο αν ξέρω το Τ, γιατί Β_bar = T^(-1)*B. (Το Α_bar βρίσκεται αλλιώς). Πώς λύνεται μια τέτοια άσκηση;
*λύθηκε: είναι απλά από τον τύπο της ελέγξιμης μορφής, το Β είναι [1 0 0 .... 0]
*λύθηκε: είναι απλά από τον τύπο της ελέγξιμης μορφής, το Β είναι [1 0 0 .... 0]
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: προφιτερόλ on June 09, 2019, 17:21:11 pm
Όταν θέλω να φέρω το σύστημα στην κανονική ελέγξιμη μορφή, πρέπει να βρω τον πίνακα Τ για τον μετασχηματισμό z=Tx. Αυτός βρίσκεται μέσω του τύπου: Τ = M_bar*M^(-1). Για να βρω το M_bar όμως, χρειάζομαι το B_bar. Αλλά το B_bar προκύπτει μόνο αν ξέρω το Τ, γιατί Β_bar = T^(-1)*B. (Το Α_bar βρίσκεται αλλιώς). Πώς λύνεται μια τέτοια άσκηση;
Αν δεις στις σημειώσεις σελ 62, σου δινει την ελεγξιμη κανονικη μορφη δηλαδη τον πίνακα Α_bar και τον Β_bar.
Αν εννοείς μια ασκηση σαν το θέμα 3/ Ιουνιος 2017 τοτε παιρνεις det(sI-A)=0, βρισκεις τα a1, a2 κτλ και τα αντικαθιστας σαν στοιχεια του Α_bar και ο Β_bar= [ 1 0 ]T
δεν ξερω αν τα εξηγω καλα ::)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Bojack Horseman on June 09, 2019, 17:39:14 pm
Αν δεις στις σημειώσεις σελ 62, σου δινει την ελεγξιμη κανονικη μορφη δηλαδη τον πίνακα Α_bar και τον Β_bar.
Αν εννοείς μια ασκηση σαν το θέμα 3/ Ιουνιος 2017 τοτε παιρνεις det(sI-A)=0, βρισκεις τα a1, a2 κτλ και τα αντικαθιστας σαν στοιχεια του Α_bar και ο Β_bar= [ 1 0 ]T
δεν ξερω αν τα εξηγω καλα ::)
Αν εννοείς μια ασκηση σαν το θέμα 3/ Ιουνιος 2017 τοτε παιρνεις det(sI-A)=0, βρισκεις τα a1, a2 κτλ και τα αντικαθιστας σαν στοιχεια του Α_bar και ο Β_bar= [ 1 0 ]T
δεν ξερω αν τα εξηγω καλα ::)
ναι ευχαριστώ. :) Το είχα μπερδέψει απλά με το σπάσιμο σε ελέγξιμο και μη ελέγξιμο μέρος, που είχε και αυτό πίνακα Τ. Αλλά είναι άλλη διαδικασία
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ctsompos on August 13, 2019, 13:24:22 pm
Στις σημειώσεις σελ 73 πως βγαίνει ο πίνακας P? (κάπως αναλυτικά αν γίνεται :P)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on August 13, 2019, 13:36:49 pm
Λύσε ((A-B*K)^T) *P + P*(A-B*K) = -Q ως προς P όπου Q = I
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ctsompos on August 13, 2019, 17:02:09 pm
ευχαριστώ!
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on August 15, 2019, 13:36:09 pm
Αν ένα σύστημα έχει πολλαπλά σημεία ισορροπίας και όλα είναι ασυμπτωτικά ευσταθή τότε αυτά από μόνα τους προσδιορίζουν το σύστημα για το αν είναι ευσταθές?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mermaid on August 15, 2019, 15:05:01 pm
Αν ένα σύστημα έχει πολλαπλά σημεία ισορροπίας και όλα είναι ασυμπτωτικά ευσταθή τότε αυτά από μόνα τους προσδιορίζουν το σύστημα για το αν είναι ευσταθές?
Ναι. Το σύστημα είναι ευσταθες οταν ολα τα σημεια ισορροπίας του είναι ευσταθη.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on August 18, 2019, 15:12:39 pm
Σε αυτήν την άσκηση παίρνει σαν ελεγκτή εισόδου u=-2a*sin(x1)-x2*cos(x1)
(https://i.imgur.com/LPRYrH5.png)
(https://i.imgur.com/ORWazY1.png)
όμως στο καινούριο σύστημα που προκύπτει με την επιλογή του u και την αντικατάσταση στο x2_dot υπάρχει και άλλο σημείο ισορροπίας το x1* = arccos(1/2a) kai x2* = 0 με 1/(2α) <1 γιατί α>1/2
Θα πρέπει να μελετήσουμε την ευστάθεια και εκείνου του σημείου ισορροπίας?
(https://i.imgur.com/LPRYrH5.png)
(https://i.imgur.com/ORWazY1.png)
όμως στο καινούριο σύστημα που προκύπτει με την επιλογή του u και την αντικατάσταση στο x2_dot υπάρχει και άλλο σημείο ισορροπίας το x1* = arccos(1/2a) kai x2* = 0 με 1/(2α) <1 γιατί α>1/2
Θα πρέπει να μελετήσουμε την ευστάθεια και εκείνου του σημείου ισορροπίας?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mermaid on August 18, 2019, 15:58:27 pm
Ειχα σημειωσει οτι το να βρουμε ελεγκτη που να επιφερει ισορροπια στην επανω κατακορυφη θεση του εκκρεμους για εμας σημαινει να αποδειξουμε οτι το (0,0) ειναι ασυμπτωτικα ευσταθες σημειο ισορροπιας, δηλαδη ζηταει να αποδειξουμε ευσταθεια σημειου και οχι ολου του συστηματος αρα νομιζω πως πρεπει να ασχοληθουμε μονο με το συγκεκριμενο ΣΙ.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on August 18, 2019, 16:05:19 pm
ευχαριστώ ;)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: pesto80 on August 20, 2019, 19:17:41 pm
"Να μελετηθεί η ευσταθεια του συτηματος χρησιμοποιωντας επιχειρηματα Lyapunov" . Σε αυτο το ερώτημα πριν πάρουμε την Lyapunov δεν πρεπει ΠΑΝΤΑ να βρίσκουμε πρωτα το ΣΙ ; (και λογικα να το βρισκουμε και ίσο με μηδεν ).
Ρωτάω γτ στα λυμενα των Downloads Σεπτ14/Θεμα 3 δεν το βρίσκει αλλά μάλλον θα το θεωρεί τετριμένο καθώς ευκολα προκύπτει μετα την αντικατάσταση του u.
Ρωτάω γτ στα λυμενα των Downloads Σεπτ14/Θεμα 3 δεν το βρίσκει αλλά μάλλον θα το θεωρεί τετριμένο καθώς ευκολα προκύπτει μετα την αντικατάσταση του u.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mermaid on August 20, 2019, 21:14:04 pm
Ναι πρέπει να βρεις τα ΣΙ και κανεις Lyapunov για το καθένα ξεχωριστά, να δεις αν ειναι ευσταθη και να βγάλεις συμπέρασμα και για το σύστημα.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Argirios on August 24, 2019, 18:30:51 pm
Αμα η παραγωγος της lyapunov βγαινει 0 σημαινει κατι η εχω κανει λαθος?
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Spiral on August 24, 2019, 18:47:56 pm
αν η παράγωγος της V κάνει 0 λογικά το σημείο ισορροπίας ειναι οριακά ευσταθές
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: stan14 on August 26, 2019, 00:57:27 am
Λύση θέμα 1 του Σεπτεμβρίου 2014 το β ερώτημα η λύση είναι σωστή?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: stan14 on August 26, 2019, 01:02:20 am
Γιατί βάζει ελεγκτή και στο παλιό και στο νέο σύστημα?
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: electric67 on February 10, 2020, 15:42:40 pm
Γενικά σταθεροποιησιμοτητα και ευστάθεια είναι το ίδιο πράγμα;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ροζ θορυβος on February 10, 2020, 17:05:41 pm
@electric67 σταθεροποιησιμοτητα έχει να κάνει με το να κρατήσεις την έξοδο σε μια επιθυμητή σταθερή τιμή. ένας τρόπος να την εξετάσεις είναι η ελεγξιμοτητα. ένα ελεγξιμο σύστημα είναι σταθεροποιησιμο, ένα σταθεροποιησιμο δεν είναι απαραίτητα ελεγξιμο.
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on February 10, 2020, 17:11:21 pm
Στο θέμα 2 του Σεπτέμβρη 2019 που λέει να γραμμικοποιηθεί το σύστημα μέσω ανάδρασης τι εννοεί;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ροζ θορυβος on February 10, 2020, 17:24:00 pm
@Theoxwriths στο α η στο γ?
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on February 10, 2020, 17:25:19 pm
Στο Α.
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: windwaker on February 10, 2020, 17:28:02 pm
Στο Α.
Σελίδα 51 Καναβούρα.Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: ροζ θορυβος on February 10, 2020, 17:31:14 pm
@theoxwriths εννοεί ότι γραμμικοποιεις το σύστημα με ανάδραση και το πέτυχαινεις μέσω του ελεγκτή. δηλαδή θα τον θέσεις σε μια μορφή που να απαλείφει τις μη γραμμικότητες, στην προκειμένη αυτά τα ημιτονα.( Η ανάδραση έγκειται στο ότι περιέχει τις καταστάσεις και μάλιστα ολόκληρα κομμάτια της εξίσωσης που περιγράφει το σύστημα - πχ τα ημιτονα είναι κομμάτια του συστηματος).
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on February 10, 2020, 17:50:33 pm
Σας ευχαριστώ πολύ και τους δύο. Για το θέμα 3, ερώτημα β, Σεπτεμβριος 2019 έχετε καμία ιδέα;
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: windwaker on February 10, 2020, 18:12:20 pm
Σας ευχαριστώ πολύ και τους δύο. Για το θέμα 3, ερώτημα β, Σεπτεμβριος 2019 έχετε καμία ιδέα;
Πρέπει να είναι μια λίγο πιο περίπλοκη εκδοχή του Θέματος 1 Σεπτεμβρίου 2016...Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: Theoxwriths on February 10, 2020, 19:18:35 pm
Οκ ευχαριστώ!
Title: Re: [ΣΑΕ ΙΙ] Απορίες σε ασκήσεις 2019
Post by: mpraskafoutas on February 10, 2020, 19:52:39 pm
Σας ευχαριστώ πολύ και τους δύο. Για το θέμα 3, ερώτημα β, Σεπτεμβριος 2019 έχετε καμία ιδέα;
πρέπει να βρεις τη Lyapunov V=1/2 * x22 + ολοκλήρωμα {g(y)d(y)} από 0 έως x1
μετά βγαίνει εύκολα.
στο θέμα 2γ) του Σεπτεμβρίου 19, αρκεί ο ελεγκτής u=x12; Έτσι βγαίνει ότι x2(t) = x2(0), άρα σταθερό. Ή μήπως θέλει να γραμμικοποιηθεί το σύστημα στη γειτονιά του σημείου ισορροπίας (0,0), για να βγει ότι sinx2 ~= x2;