Title: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μεταλλαγμένη Πάπια on June 01, 2016, 20:46:38 pm
Απλα να ενημερωσω, ανεβασα δικες μου λυσεις για αρκετα θεματα στα downloads. Νομιζω οτι ειναι σωστα, αλλα ειμαι ανοιχτος σε συζητηση :D :D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: K on June 02, 2016, 15:42:51 pm
Ευχαριστούμε πολύ Μεταλλαγμένη Πάπια.
Και σε ενιαίο pdf για τη διευκόλυνση του κοινού :
http://www.filedropper.com/thematasaeiicompressed
all copyrights reserved by Μεταλλαγμένη Πάπια (https://www.thmmy.gr/smf/index.php?action=profile;u=13688)
Και σε ενιαίο pdf για τη διευκόλυνση του κοινού :
http://www.filedropper.com/thematasaeiicompressed
all copyrights reserved by Μεταλλαγμένη Πάπια (https://www.thmmy.gr/smf/index.php?action=profile;u=13688)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Σα τανυστής on June 05, 2016, 15:14:44 pm
στην φετινη προοδο (2016) στις λυσεις στο 1 β) καταληγει μετα απο γραμμικοποιηση στο ΣΙ να λεει ολοι οι συντελεστες ομοσημοι αρα ολες οι ριζες στο αριστερο ημιεπιπεδο. Αυτο απο που ειναι (routh κριτηριο?) Ισχυει παντα ετσι? Δεν ηταν κατι με πινακακια κλπ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Dealan on June 05, 2016, 17:12:40 pm
Ναι, κριτήριο Routh είναι.
Κάπου λέει στη θεωρία πως ο αριθμώς ριζών στο θετικό ημιεπίπεδο είναι ίσος με το πόσες φορές οι συντελεστές του Routh αλλάζουν πρόσημο.
Κάπου λέει στη θεωρία πως ο αριθμώς ριζών στο θετικό ημιεπίπεδο είναι ίσος με το πόσες φορές οι συντελεστές του Routh αλλάζουν πρόσημο.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: anaslout on June 06, 2016, 02:16:29 am
καλησπερα παιδια,για το θεμα 3 της εξεταστικης φεβρουαριου 2016,εχεις κανεις ιδεα πως θα κανουμε την γραμμικοποιηση μεσω αναδρασης?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: El Niño on June 06, 2016, 02:17:43 am
καλησπερα παιδια,για το θεμα 3 της εξεταστικης φεβρουαριου 2016,εχεις κανεις ιδεα πως θα κανουμε την γραμμικοποιηση μεσω αναδρασης?
πηγαινε στο αρχειο sae_shm , σελιδα 3 ολοιδιοTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: sotiristsar on June 06, 2016, 17:35:44 pm
Παιδιά μήπως έχει λύσει κάποιος το 1ο θέμα φλεβάρη του 2016???
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: nvog1993 on June 06, 2016, 17:46:43 pm
Παιδιά μήπως έχει λύσει κάποιος το 1ο θέμα φλεβάρη του 2016???
Σελ 36 από σημειώσεις exomag. Θες ουσιαστικά το σύστημα που θα προκύψει να είναι ελέγξιμο.Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Σα τανυστής on June 06, 2016, 18:30:56 pm
φεβ 16 θεμα 2 πρεπει να το χωρισουμε σε ελεγξιμο και μη ελεγξιμο? Ποιον Τ διαλεγετε?
ακυρο ειμαι χαϊβανι κοιταγα λαθος πινακα και δε μου βγαινε..
ακυρο ειμαι χαϊβανι κοιταγα λαθος πινακα και δε μου βγαινε..
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: gmtms on June 06, 2016, 19:19:34 pm
φεβ 16 θεμα 2 πρεπει να το χωρισουμε σε ελεγξιμο και μη ελεγξιμο? Ποιον Τ διαλεγετε?
ακυρο ειμαι χαϊβανι κοιταγα λαθος πινακα και δε μου βγαινε..
πες κι εμάς πώς το λυσεςακυρο ειμαι χαϊβανι κοιταγα λαθος πινακα και δε μου βγαινε..
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Σα τανυστής on June 06, 2016, 19:28:44 pm
δεν ειμαι προ οποτε δεν ορκιζομαι για τη λυση. Αν ειναι κανας σχετικος και δει λαθος πειτε.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: gmtms on June 06, 2016, 19:33:23 pm
Ευχαριστώ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μεταλλαγμένη Πάπια on June 06, 2016, 20:02:28 pm
δεν ειμαι προ οποτε δεν ορκιζομαι για τη λυση. Αν ειναι κανας σχετικος και δει λαθος πειτε.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Σωστος εισαι. Στο Τ επισης μη σκεφτεσαι μονο την οριζουσα, σκεψου και πως να κανεις τη ζωη σου ευκολη. Οπου μπορεις να βαλεις 0 για να κανεις λιγοτερες πραξεις, βαλε :)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mfilip on June 06, 2016, 21:47:12 pm
Φεβρουάριος 2016 θεμα 3 καμιά ιδέα? όταν ζητάει γραμμικοποίηση μέσω ανάδρασης είναι το ίδιο με το να ζητάει γραμμικοποίηση γύρω από το σημείο ισορροπίας?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: nvog1993 on June 06, 2016, 21:55:00 pm
Φεβρουάριος 2016 θεμα 3 καμιά ιδέα? όταν ζητάει γραμμικοποίηση μέσω ανάδρασης είναι το ίδιο με το να ζητάει γραμμικοποίηση γύρω από το σημείο ισορροπίας?
Όταν ζητάει γενικά γραμμικοποίηση μέσω ανάδρασης σημαίνει ότι πρέπει να επιλέξεις το u έτσι ώστε το σύστημα να γίνει γραμμικό. Για το συγκεκριμένο έχει μια μεθοδολογία στα επιπλέον παραδείγματα σημειώσεων. Αν σου πει γραμμικοποίηση γύρω από ΣΙ, τότε πας με ανάπτυγμα Taylor και ακολουθείς τη γνωστή διαδικασία. Οι δύο γραμμικοποιήσεις διαφέρουν.Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: emmae on June 06, 2016, 22:02:23 pm
Όταν ζητάει γενικά γραμμικοποίηση μέσω ανάδρασης σημαίνει ότι πρέπει να επιλέξεις το u έτσι ώστε το σύστημα να γίνει γραμμικό. Για το συγκεκριμένο έχει μια μεθοδολογία στα επιπλέον παραδείγματα σημειώσεων. Αν σου πει γραμμικοποίηση γύρω από ΣΙ, τότε πας με ανάπτυγμα Taylor και ακολουθείς τη γνωστή διαδικασία. Οι δύο γραμμικοποιήσεις διαφέρουν.
Iακωβιανο πινακα κλπ κλπ κλπ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: claus on June 06, 2016, 22:23:43 pm
δεν ειμαι προ οποτε δεν ορκιζομαι για τη λυση. Αν ειναι κανας σχετικος και δει λαθος πειτε.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Νομίζω πρέπει να δεις και τον πίνακα Β'=Τ-1Β να έχει πρώτη γραμμή 1 και δεύετρη 0.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: galexang on June 06, 2016, 23:36:58 pm
Για το 3ο θέμα Φλεβάρη 2016 έχεις κάποιος ιδέα πως γίνεται;..Πρέπει μηπως να υποθέσουμε απο μόνοι μας οτι ο πίνακας Α(q) αντιστρέφεται;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: El Niño on June 07, 2016, 02:48:27 am
Για το 3ο θέμα Φλεβάρη 2016 έχεις κάποιος ιδέα πως γίνεται;..Πρέπει μηπως να υποθέσουμε απο μόνοι μας οτι ο πίνακας Α(q) αντιστρέφεται;
πολλαπλασιασε με Α^-1 ναι, αν θυμαμαι καλαTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mpimpa on June 07, 2016, 10:23:18 am
Μια βοηθεια παρακαλώ! Γιατί δεν μου βγαίνει το μηδενικό εκεί που πρέπει??
δεν ειμαι προ οποτε δεν ορκιζομαι για τη λυση. Αν ειναι κανας σχετικος και δει λαθος πειτε.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μεταλλαγμένη Πάπια on June 07, 2016, 11:00:46 am
Μια βοηθεια παρακαλώ! Γιατί δεν μου βγαίνει το μηδενικό εκεί που πρέπει??
O αντιστροφος σου ειναι λαθος. Ετσι πρεπει:
(https://www.mathsisfun.com/algebra/images/matrix-inverse-2x2.gif)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: JakeLaMotta on June 07, 2016, 16:17:13 pm
Στο θέμα 1 του Φεβρουαρίου 2016 τι ακριβώς θέλει??
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Σα τανυστής on June 07, 2016, 16:36:13 pm
Στο θέμα 1 του Φεβρουαρίου 2016 τι ακριβώς θέλει??
να δειξεις οτι ειναι ελεγξιμο καταλαβαινω εγω, το χει σημειωσεις εξομαγκ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: JakeLaMotta on June 07, 2016, 16:46:08 pm
να δειξεις οτι ειναι ελεγξιμο καταλαβαινω εγω, το χει σημειωσεις εξομαγκ
Ναι,αυτό το έχω δει.Απλά λέει "με κατάλληλη επιλογή της τάσης εισόδου u(t)".Αυτό με μπερδεύει λίγο όσον αφορά το τι ακριβώς θέλει να δείξουμε
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Dealan on June 07, 2016, 16:52:25 pm
Απλά σου λέει έναν ορισμό την ελεγξιμότητας αντί για τον ίδιο τον όρο γαι να σε μπερδέψει.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: JakeLaMotta on June 07, 2016, 16:59:35 pm
Απλά σου λέει έναν ορισμό την ελεγξιμότητας αντί για τον ίδιο τον όρο γαι να σε μπερδέψει.
Ναι,αφού ουσιαστικά η τάση εισόδου εδώ είναι η είσοδος ελέγχου που αναφέρει στον ορισμό της ελεγξιμότητας.Κομπλέ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mfilip on June 07, 2016, 18:47:19 pm
μπορει να ανεβασει καποιος αναλυτικη λυση του 3ου θεματος του φεβρουαριου 16 και του 3ου θεματος σεπτεμβριου του 15?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mfilip on June 07, 2016, 18:56:43 pm
Όταν ζητάει γενικά γραμμικοποίηση μέσω ανάδρασης σημαίνει ότι πρέπει να επιλέξεις το u έτσι ώστε το σύστημα να γίνει γραμμικό. Για το συγκεκριμένο έχει μια μεθοδολογία στα επιπλέον παραδείγματα σημειώσεων. Αν σου πει γραμμικοποίηση γύρω από ΣΙ, τότε πας με ανάπτυγμα Taylor και ακολουθείς τη γνωστή διαδικασία. Οι δύο γραμμικοποιήσεις διαφέρουν.
μηπως θα μπορουσες να μου γραψεις λιγο και τη λυση?Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: nvog1993 on June 07, 2016, 19:20:47 pm
μπορει να ανεβασει καποιος αναλυτικη λυση του 3ου θεματος του φεβρουαριου 16 και του 3ου θεματος σεπτεμβριου του 15?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mfilip on June 07, 2016, 19:22:37 pm
να σαι καλα φιλε!!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: JakeLaMotta on June 08, 2016, 01:37:20 am
Για το 2ο θέμα Φεβρουαρίου 2016
Στη 2η στήλη του πίνακα Τ μπορούμε να βάλουμε ότι θέλουμε αρκεί να μη μηδενίζεται η ορίζουσα??Γιατί αν βάλω ότι θέλω στη 2η στήλη(π.χ. εγώ έβαλα [1 0]),ο πίνακας μετά ούτε 0 κάτω αριστερά μου βγάζει ούτε αρνητικό το κάτω δεξιά....
δεν ειμαι προ οποτε δεν ορκιζομαι για τη λυση. Αν ειναι κανας σχετικος και δει λαθος πειτε.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Λοιπον,
Πας τσεκαρεις τον Μ =[Β ΑΒ] βλεπεις βγαινει 0 η οριζουσα. Οποτε απο σημειωσεις εξομαγκ σελ 38 πας και κανεις εκεινο που το χωριζεις σε ενα ελεγξιμο ζευγος και σε ενα οχι. Εκει το θεμα ειναι να βρεις τον Τ για να κανεις το Τ-1ΑΤ (προσεχε οτι αρχιζεις με x=Tz). Ο ροβι στο pdf, για να χτιστει αυτος ο Τ, λεει παρε τις καμποσες ανεξαρτητες γραμμικα στηλες του Μ (εγω κοιτουσα τον Α αντι για Μ και δε μου βγαινε) , οποτε εδω παιρνεις την 1η. Την 2η για να συμπληρωθει ο πινακας την διαλεγεις εσυ ωστε να μη μηδενιζεται η οριζουσα.
Μετα πας κανεις πολλ/σμο το Τ-1ΑΤ και φτιαχνεται ενας πινακας που θα χει κατω αριστερα 0 και τερμα δεξια αυτο του μη ελεγξιμου μερους. Ε αυτον τον πινακα τερμα κατω δεξια (που εδω ειναι 1χ1) τον θες οπως παντα ιδιοτιμες στο αριστερο ημιεπιπεδο. Επειδη ειναι νουμερο, βγαινει αρνητικο οποτε εισαι οκ.
Στη 2η στήλη του πίνακα Τ μπορούμε να βάλουμε ότι θέλουμε αρκεί να μη μηδενίζεται η ορίζουσα??Γιατί αν βάλω ότι θέλω στη 2η στήλη(π.χ. εγώ έβαλα [1 0]),ο πίνακας μετά ούτε 0 κάτω αριστερά μου βγάζει ούτε αρνητικό το κάτω δεξιά....
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Dealan on June 08, 2016, 07:00:47 am
Σίγουρα έκανες σωστά πράξεις; Και εγώ [1 0] έβαλα και από ότι θυμάμαι μου έβγαινε.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 12, 2016, 21:34:36 pm
λοιπόν στο θέμα 3 ιούνιος 2016 θεώρησα συνάρτηση Lyapunov V(x) = 1/2 x12 + 1/2 x22. μετά με παραγώγιση και με επιλογή του ελεγκτή ο οποίος περιέχει μόνο μετρήσιμα μεγέθη έχω κάνει απαλοιφή όλων των όρων εκτός του -x2^2 οπότε η παράγωγος είναι αρνητικά ημιορισμένη, άρα χρειάζομαι και θ. Lasalle. μπορώ στο θ. Lasalle να θεωρήσω ότι u = 0 στην έκφραση του x'2 για έχω μοναδικό αμετάβλητο σύνολο το σημείο 0,0?
σόρρυ η ερώτηση δεν είναι τόσο καλά διατυπωμένη.
σόρρυ η ερώτηση δεν είναι τόσο καλά διατυπωμένη.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: heavy melon on September 13, 2016, 15:40:03 pm
Ιούνης 2016, θέμα 3ο
χρειάζεται Lasalle όντως? το γεγονός ότι dV(x)/dx<0 και ίση με 0 μόνο για x2=0
δεν μας οδηγεί απευθείας σε ασυμπτωτική ευστάθεια?
Lasalle παίρνουμε για το "ολικό" που ζητάει?
χρειάζεται Lasalle όντως? το γεγονός ότι dV(x)/dx<0 και ίση με 0 μόνο για x2=0
δεν μας οδηγεί απευθείας σε ασυμπτωτική ευστάθεια?
Lasalle παίρνουμε για το "ολικό" που ζητάει?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: jimPster on September 13, 2016, 16:47:30 pm
πρεπει χ1=0 χ2=0 για να ισχυει αυτο που λες ενω ισχυει για χ2=0 χ1=οτιδηποτε
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 13, 2016, 16:50:44 pm
Ιούνης 2016, θέμα 3ο
χρειάζεται Lasalle όντως? το γεγονός ότι dV(x)/dx<0 και ίση με 0 μόνο για x2=0
δεν μας οδηγεί απευθείας σε ασυμπτωτική ευστάθεια?
Lasalle παίρνουμε για το "ολικό" που ζητάει?
χρειάζεται Lasalle όντως? το γεγονός ότι dV(x)/dx<0 και ίση με 0 μόνο για x2=0
δεν μας οδηγεί απευθείας σε ασυμπτωτική ευστάθεια?
Lasalle παίρνουμε για το "ολικό" που ζητάει?
ίσως αν διαλέξεις καλό ελεγκτή και μπορείς να είσαι σίγουρη ότι η παράγωγος της Lyap είναι αρνητικά ορισμένη να μπορείς να το βγάλεις και χωρίς Lasalle.
Τι ελεγκτή όρισες;
Εγώ έβαλα u = 1/x2*[-x1x2+3x12 + x22sin(x1)] - x2.
Γενικά δεν είμαι σίγουρος για το τι επιτρέπεται να κάνω και πόση ελευθερία μπορεί να έχω στην επιλογή του ελεγκτή. Εγώ αυτό το έκανα για να διώξω τους όρους για τους οποίους δεν είμαι σίγουρος για το πρόσημο και να μείνει στην παράγωγο Lyap μόνο -x22, άρα αρνητικά ημιορισμένη, άρα Lasalle.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: xameno kormi on September 13, 2016, 17:10:38 pm
το Lasalle μετα πως το διατυπώνεις για χ2=0 εχοντας βαλει στον ελεγκτη τον ορο 1/χ2 ? με τι ειναι ισο το χ2 ' ? (δεν ξερω αν χρειαζεται κιολας στην διατυπωση αλλα εχοντας βαλει 1/χ2 δεν μπορεις να το βρεις ετσι δεν ειναι ? )
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 13, 2016, 17:20:25 pm
το Lasalle μετα πως το διατυπώνεις για χ2=0 εχοντας βαλει στον ελεγκτη τον ορο 1/χ2 ? με τι ειναι ισο το χ2 ' ? (δεν ξερω αν χρειαζεται κιολας στην διατυπωση αλλα εχοντας βαλει 1/χ2 δεν μπορεις να το βρεις ετσι δεν ειναι ? )
δεν το σκέφτηκα! :-\
θα το δω ξανά και θα επανέρθω.
εσύ τι ελεγκτή όρισες;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: heavy melon on September 13, 2016, 17:29:10 pm
Οκ thanks
εγω παιρνω συνηθως την τετραγωνικη μορφη κι οχι κατι πολυ ευφανταστο :P
εγω παιρνω συνηθως την τετραγωνικη μορφη κι οχι κατι πολυ ευφανταστο :P
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 13, 2016, 17:32:49 pm
Οκ thanks
εγω παιρνω συνηθως την τετραγωνικη μορφη κι οχι κατι πολυ ευφανταστο :P
εγω παιρνω συνηθως την τετραγωνικη μορφη κι οχι κατι πολυ ευφανταστο :P
και εγώ με τετραγωνική Lyap προσπαθώ να το βγάλω. με τι ελεγκτή το έλυσες τελικά;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: jimPster on September 13, 2016, 17:37:19 pm
ωραια μαλλον γτ τα μπερδεψε η απο πανω
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 - x2 εχουμε
(V)' = -x2^2 <=0 και μετα lassalle
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 - x2 εχουμε
(V)' = -x2^2 <=0 και μετα lassalle
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 13, 2016, 17:39:13 pm
ωραια μαλλον γτ τα μπερδεψε η απο πανω
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 + x2 εχουμε
(V)' = x2^2 <=0 και μετα lassalle
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 + x2 εχουμε
(V)' = x2^2 <=0 και μετα lassalle
ωραία και εγώ έτσι το πήγα τελικά μετά την πατάτα που είχα κάνει στον 1ο ελεγκτή!
γενικά ο μόνος περιορισμός από ότι έχω καταλάβει σε τέτοιους ελεγκτές είναι να είναι όλα τα μεγέθη που προσθέτουμε μετρήσιμα.
στον ιούλιο του 16 επίσης, στο θέμα 1ο ερώτημα γ το βγάζετε και εσείς μη-παρατηρήσιμο;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: jimPster on September 13, 2016, 17:43:17 pm
και κατι τελευταιο, σημαντικο ομως, θα δειξεις πρωτα οτι ειναι μοναδικο ΣΙ γτ αν εχει παραπανω απο 1 δεν γινεται να εχουμε ολικη ευσταθεια ( αν δεν τ κανεις σιγουρα θα κοψει) Για κατι τετοια ζει ο Ροβιθακης
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 13, 2016, 17:48:28 pm
και κατι τελευταιο, σημαντικο ομως, θα δειξεις πρωτα οτι ειναι μοναδικο ΣΙ γτ αν εχει παραπανω απο 1 δεν γινεται να εχουμε ολικη ευσταθεια ( αν δεν τ κανεις σιγουρα θα κοψει) Για κατι τετοια ζει ο Ροβιθακης
ωωωω, σωστά! :o
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: xameno kormi on September 13, 2016, 17:55:24 pm
ωραια μαλλον γτ τα μπερδεψε η απο πανω
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 - x2 εχουμε
(V)' = x2^2 <=0 και μετα lassalle
εχουμε V(x1,x2) = 1/2(x1^2 + x2^2)
παραγωγος (V)'= χ1(χ1)' + χ2(χ2)' =αντικαθιστουμε τα (χ1)',(χ2)' απο εξισωσεις καταστασεις
Αρα (V)' = x1x2 + x2(-3x1^2 - x2sinx1 + u)
Αρα για u = 3x1^2 + x2sinx1 -x1 - x2 εχουμε
(V)' = x2^2 <=0 και μετα lassalle
αυτο εκανα και γω στην διατυπωση του Lassalle λες οτι προκυπτει
x1 ' = x2
x2 ' = -x1
αρα λες οτι ξεκινωντας απο μια λυση (α,0) αφου x2=0 θα εχεις x2'= -α αρα ξεφευγεις απο το 0 δηλαδη απο το συνολο S αρα το μονο που δεν ξεφευγει απο το S ειναι το σημειο (0,0) και αρα το μεγαλυτερο αμεταβλητο συνολο ειναι το (0,0) αρα ασυμπτωτικα ολικα ευσταθες?
και κατι τελευταιο, σημαντικο ομως, θα δειξεις πρωτα οτι ειναι μοναδικο ΣΙ γτ αν εχει παραπανω απο 1 δεν γινεται να εχουμε ολικη ευσταθεια ( αν δεν τ κανεις σιγουρα θα κοψει) Για κατι τετοια ζει ο Ροβιθακης
αντικαθιστω τον ελεγκτη και λυνω για να δειξω οτι ειναι το μοναδικο ;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: jimPster on September 13, 2016, 17:58:13 pm
Μου φαινεται παιρνεις τις εξισωσεις καταστασης για u=0 και λυνεις (x1)' = 0, (x2)'=0
Για Lassale οπως τα λες απο σημειωσεις, μπορει να θελει να πεις οτι ειναι και το μοναδικο αμεταβλητο συνολο
Για Lassale οπως τα λες απο σημειωσεις, μπορει να θελει να πεις οτι ειναι και το μοναδικο αμεταβλητο συνολο
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: orestisk4 on September 14, 2016, 11:12:26 am
Στο Θέμα 1 (γ) Ιούνιος 2016, που ζητά έλεγχο για παρατηρησιμότητα όταν η έξοδος είναι γραμμικός συνδυασμός των μεταβλητών κατάστασης, εγώ έκανα το εξής:
Είπα έστω y = -k1*x1-k2*x2 = [ -k1 -k2]x = Cx και κατόπιν βρήκα τον πίνακα W με C και CA και από την ορίζουσα είδα απλά ότι για οποιοδήποτε k1,k2 αν ισχύει R1C1 = R2C2 βγαίνει πάντα 0 και rank(W) = 1. Οπότε δεν είναι παρατηρήσιμος. Σωστό ή θέλει κάτι άλλο;
Είπα έστω y = -k1*x1-k2*x2 = [ -k1 -k2]x = Cx και κατόπιν βρήκα τον πίνακα W με C και CA και από την ορίζουσα είδα απλά ότι για οποιοδήποτε k1,k2 αν ισχύει R1C1 = R2C2 βγαίνει πάντα 0 και rank(W) = 1. Οπότε δεν είναι παρατηρήσιμος. Σωστό ή θέλει κάτι άλλο;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 14, 2016, 12:08:04 pm
Στο Θέμα 1 (γ) Ιούνιος 2016, που ζητά έλεγχο για παρατηρησιμότητα όταν η έξοδος είναι γραμμικός συνδυασμός των μεταβλητών κατάστασης, εγώ έκανα το εξής:
Είπα έστω y = -k1*x1-k2*x2 = [ -k1 -k2]x = Cx και κατόπιν βρήκα τον πίνακα W με C και CA και από την ορίζουσα είδα απλά ότι για οποιοδήποτε k1,k2 αν ισχύει R1C1 = R2C2 βγαίνει πάντα 0 και rank(W) = 1. Οπότε δεν είναι παρατηρήσιμος. Σωστό ή θέλει κάτι άλλο;
Είπα έστω y = -k1*x1-k2*x2 = [ -k1 -k2]x = Cx και κατόπιν βρήκα τον πίνακα W με C και CA και από την ορίζουσα είδα απλά ότι για οποιοδήποτε k1,k2 αν ισχύει R1C1 = R2C2 βγαίνει πάντα 0 και rank(W) = 1. Οπότε δεν είναι παρατηρήσιμος. Σωστό ή θέλει κάτι άλλο;
και εγώ έτσι το πήγα και κατέληξα στο ίδιο συμπέρασμα. δεν νομίζω να χρειάζεται κάτι παραπάνω.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Αλντεμπαράν on September 14, 2016, 17:42:36 pm
μήπως είδε κάποιος το 3ο θέμα της πτυχιακής φεβρουαρίου 2016;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Escobar on September 14, 2016, 18:14:32 pm
μήπως είδε κάποιος το 3ο θέμα της πτυχιακής φεβρουαρίου 2016;
Και εγώ κάτι παρόμοιο με τη λύση (https://www.thmmy.gr/smf/index.php?topic=72015.msg1130417#msg1130417)που έδωσε πιο πίσω o nvog σκέφτηκα, αλλά δε ξέρω αν είναι σωστή. Την είδες και δεν σου άρεσε?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 14, 2016, 18:25:09 pm
Και εγώ κάτι παρόμοιο με τη λύση (https://www.thmmy.gr/smf/index.php?topic=32998.msg1130417#msg1130417)που έδωσε πιο πίσω o nvog σκέφτηκα, αλλά δε ξέρω αν είναι σωστή. Την είδες και δεν σου άρεσε?
ρε συ, και εγώ έτσι το σκέφτηκα αλλά είναι δυνατόν για μια αντικατάσταση να έδινε 4 μονάδες;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Escobar on September 14, 2016, 18:38:24 pm
ρε συ, και εγώ έτσι το σκέφτηκα αλλά είναι δυνατόν για μια αντικατάσταση να έδινε 4 μονάδες;
αν δεν είναι τρολιά, ίσως παίζει ρόλο το ότι τα q και q_dot είναι διανύσματα στην άσκηση και όχι βαθμωτά μεγέθη όπως στις άλλες παρόμοιες, οπότε τα x1 και x2 που θέτουμε δεν είναι οι γνωστές εξισώσεις κατάστασης, αλλά απλά δύο νέα διανύσματα..Βέβαια ήταν και πτυχιακή, μπορεί να ήθελε να βοηθήσει απλά κόσμο που λογικά θα είχε αφήσει τα σαε για το πτυχίο οπότε να ήταν όντως απλή. Ας απαντήσει κάποιος που ξέρει σίγουρα
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: xameno kormi on September 14, 2016, 19:06:11 pm
αν δεν είναι τρολιά, ίσως παίζει ρόλο το ότι τα q και q_dot είναι διανύσματα στην άσκηση και όχι βαθμωτά μεγέθη όπως στις άλλες παρόμοιες, οπότε τα x1 και x2 που θέτουμε δεν είναι οι γνωστές εξισώσεις κατάστασης, αλλά απλά δύο νέα διανύσματα..Βέβαια ήταν και πτυχιακή, μπορεί να ήθελε να βοηθήσει απλά κόσμο που λογικά θα είχε αφήσει τα σαε για το πτυχίο οπότε να ήταν όντως απλή. Ας απαντήσει κάποιος που ξέρει σίγουρα
στις σημ exomag σελ 34 υπαρχει ενα παραδειγμα που δεν αντιστρεφει τον πινακα αλλα πρεπει να ξερεις οτι ειναι θετικα ορισμενος
στην προκειμενη μπορεις να παρεις τον ελεγκτη u=Αv+Bq'+C και να καταληξεις στο οτι Aq''=Av -> A(q''-v)=0 αρα εδω να πεις οτι πρεπει ο Α να ειναι θετικα ορισμενος και να καταληξεις στο q'' = v
βεβαια στο παραδειγμα εκεινο δεν ξερω απο που προκυπτει οτι ο M ειναι θετικα ορισμενος
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 14, 2016, 21:09:00 pm
στις σημ exomag σελ 34 υπαρχει ενα παραδειγμα που δεν αντιστρεφει τον πινακα αλλα πρεπει να ξερεις οτι ειναι θετικα ορισμενος
στην προκειμενη μπορεις να παρεις τον ελεγκτη u=Αv+Bq'+C και να καταληξεις στο οτι Aq''=Av -> A(q''-v)=0 αρα εδω να πεις οτι πρεπει ο Α να ειναι θετικα ορισμενος και να καταληξεις στο q'' = v
βεβαια στο παραδειγμα εκεινο δεν ξερω απο που προκυπτει οτι ο M ειναι θετικα ορισμενος
στην προκειμενη μπορεις να παρεις τον ελεγκτη u=Αv+Bq'+C και να καταληξεις στο οτι Aq''=Av -> A(q''-v)=0 αρα εδω να πεις οτι πρεπει ο Α να ειναι θετικα ορισμενος και να καταληξεις στο q'' = v
βεβαια στο παραδειγμα εκεινο δεν ξερω απο που προκυπτει οτι ο M ειναι θετικα ορισμενος
ναι είδα και εγώ ένα παρόμοιο παράδειγμα. φαντάζομαι αν όντως είναι τόσο απλό έπρεπε να πάρεις τουλάχιστον περιπτώσεις και αν μπορείς να διαιρέσεις με τον Α να το προχωρήσεις ένα βήμα ακόμα και να πεις ότι τελικά προκύπτει Aq'' = Av => q'' = v.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: orestisk4 on September 14, 2016, 23:48:52 pm
Ιούνιος 2016
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mitsoschelsea on September 14, 2016, 23:56:02 pm
Ιούνιος 2016
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
Αυτά βγάζω κι εγώ στα (α)-(δ)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 15, 2016, 00:06:28 am
Ιούνιος 2016
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
α) Βγάζω det(M)=-3 άρα n =2 και το σύστημα είναι πάντα ελέγξιμο
β) Το σύστημα είναι γραμμικό, οπότε ελέγχω ιδιοτιμές det(sI-A) = 0. Προκύπτει πολυώνυμο με p1=5>0 και p2=4+3α. Άρα, για να έχω ευσταθές σύστημα πρέπει p2>0 οπότε α >-4/3
γ) Θέτω α=0 και u=-k1*x1-k2*x2. Από τον πίνακα Α που βγαίνει βρίσκω πάλι ιδιοτιμές και θέλω το πολυώνυμο να ισούται με (s+6)*(s+7). Εξισώνω, οπότε βρίσκω από το σύστημα 2x2 ότι k1=10,k2=8
δ) Ξαναβρίσκω ιδιοτιμές του Α έχοντας αντικαταστήσει τα k1,k2 (έχοντας κρατήσει τώρα το α) και βρίσκω για p1=13>0, p2 = 3*(α+10)>0 ότι πρέπει α>-10
ε) Δεν ξέρω τι ακριβώς να πω. Το μόνο που σκέφτηκα είναι ότι: στο (β) ανεξαρτήτως ελεγκτή το α πρέπει να είναι μεγαλύτερο του -4/3, ενώ στο (δ) η χρήση του συγκεκριμένου ελεγκτή αυξάνει το εύρος τιμών που μπορεί
να πάρει το α (α>-10). Κάτι δεν μου κολλάει :D
Για τα (α)-(δ) πείτε γνώμη αν είναι σωστά και για το (ε) πείτε ιδέες :D
και εγώ τα ίδια βρήκα.
στο ε και εγώ κάτι παρόμοιο με το δικό σου έγραψα. σκεφτόμουν μήπως μπορείς να ότι με τον έλεγχο αυτό μάλλον έχεις καταφέρει να μεταφέρεις τις ιδιοτιμές πιο αριστερά στο αρνητικό ημιεπίπεδο οπότε πλέον το α μπορεί να πάρει τιμές σε μεγαλύτερο εύρος και το σύστημα να μένει πάλι στην ευστάθεια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: akyrosHM on September 15, 2016, 01:11:19 am
Στο β) πώς ακριβώς πήρες det(sI-A)=0? Αφού δεν έχεις σύστημα της μορφής x'= Ax, αλλά x'=Ax + Bu!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: orestisk4 on September 15, 2016, 01:31:18 am
Στο β) πώς ακριβώς πήρες det(sI-A)=0? Αφού δεν έχεις σύστημα της μορφής x'= Ax, αλλά x'=Ax + Bu!
Επειδή είναι γραμμικό το σύστημα, για να έχω ευστάθεια πρέπει οι ιδιοτιμές του Α να είναι αρνητικές. Οπότε, πήρα το det(sI-A) και έβγαλα ένα πολυώνυμο της μορφής s^2 + p1*s + p2
και είπα ότι με βάση το κριτήριο Ruth πρέπι οι συντελεστές p1,p2 να είναι θετικοί για να έχω αρνητικές ιδιοτιμές. Νομίζω αυτή είναι η λογική. Αν είναι λάθος, ας με διορθώσει κάποιος!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: orestisk4 on September 15, 2016, 01:33:10 am
Επίσης, εκεί νομίζω έγκειται και η βασική διαφορά των ερωτημάτων (β) και (δ) που ζητάει στο (ε). Πώς το U επιδρά στο α.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 15, 2016, 02:13:29 am
Επειδή είναι γραμμικό το σύστημα, για να έχω ευστάθεια πρέπει οι ιδιοτιμές του Α να είναι αρνητικές. Οπότε, πήρα το det(sI-A) και έβγαλα ένα πολυώνυμο της μορφής s^2 + p1*s + p2
και είπα ότι με βάση το κριτήριο Ruth πρέπι οι συντελεστές p1,p2 να είναι θετικοί για να έχω αρνητικές ιδιοτιμές. Νομίζω αυτή είναι η λογική. Αν είναι λάθος, ας με διορθώσει κάποιος!
και είπα ότι με βάση το κριτήριο Ruth πρέπι οι συντελεστές p1,p2 να είναι θετικοί για να έχω αρνητικές ιδιοτιμές. Νομίζω αυτή είναι η λογική. Αν είναι λάθος, ας με διορθώσει κάποιος!
Ναι αυτό έπρεπε να κάνεις, μας είχε πετάξει και μια ατάκα για να το καταλάβουμε αλλά δεν θυμάμαι ποια ήταν
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 15, 2016, 13:15:40 pm
Φεβρουαριος 2016, Θέμα 2. Οταν σχηματίζω τον Τ, ο πινακας Μ δεν εχει καμια στηλη ανεξάρτητη σωστα; Οποτε τον Τ τον σχηματιζω οπως θελω εξολοκληρου;
π.χ Τ= 1 0
0 1 ??
π.χ Τ= 1 0
0 1 ??
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Escobar on September 15, 2016, 13:27:46 pm
Φεβρουαριος 2016, Θέμα 2. Οταν σχηματίζω τον Τ, ο πινακας Μ δεν εχει καμια στηλη ανεξάρτητη σωστα; Οποτε τον Τ τον σχηματιζω οπως θελω εξολοκληρου;
π.χ Τ= 1 0
0 1 ??
π.χ Τ= 1 0
0 1 ??
παίρνεις μία στήλη από τον Μ, σίγουρα, αφού ένα διάνυσμα μόνο του είναι πάντα γραμμικώς ανεξάρτητο. Απλά, αν οι άλλες είναι γραμμικώς εξαρτημένες (σε 2χ2 σίγουρα θα είναι, αφού η ορίζουσα θα βγαίνει 0) συμπληρώνεις την άλλη στήλη του Τ με κάποιο διάνυσμα της επιλογής σου, ώστε να είναι γραμμικώς ανεξάρτητο με την στήλη του Μ που έβαλες πριν.Π.χ το [0 1]Τ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 15, 2016, 13:30:20 pm
παίρνεις μία στήλη από τον Μ, σίγουρα, αφού ένα διάνυσμα μόνο του είναι πάντα γραμμικώς ανεξάρτητο.
Ευχαριστώ πολύ! Μου είχε διαφύγει αυτο.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mitsoschelsea on September 15, 2016, 18:07:21 pm
Ιούνιος 2016, Θέμα 3.
Κάποιος που να έχει αποτελέσματα;
Κάποιος που να έχει αποτελέσματα;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 15, 2016, 18:30:58 pm
Ιούνιος 2016, Θέμα 3.
Κάποιος που να έχει αποτελέσματα;
τι αποτέλεσμα θες? (0,0) ΣΙ με Lyapunov και LassaleΚάποιος που να έχει αποτελέσματα;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mitsoschelsea on September 15, 2016, 18:42:38 pm
τι αποτέλεσμα θες? (0,0) ΣΙ με Lyapunov και Lassale
Ναι σύμφωνοι, απλά με τι ελεγκτή;
Εγώ πήρα u=x2.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 15, 2016, 18:51:15 pm
δεν θυμάμαι αλλά είχα Vdot = -x2^2( a + sinx1) όπου α > 1
δεν θυμάμαι αν είναι sin ή cos αλλά το ίδιο κάνει
δεν θυμάμαι αν είναι sin ή cos αλλά το ίδιο κάνει
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: xameno kormi on September 15, 2016, 19:01:18 pm
Ναι σύμφωνοι, απλά με τι ελεγκτή;
Εγώ πήρα u=x2.
Εγώ πήρα u=x2.
εγω πηρα ελεγκτη u=-x1-x2+x2sinx1+3x12 κατεληξα σε Vdot=-x22, επιτρεπεται αυτο ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 15, 2016, 19:02:07 pm
ναι επιτρέπεται, ότι θέλεις μπορεί να είναι θεωρητικά
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 15, 2016, 19:04:42 pm
εγω πηρα ελεγκτη u=-x1-x2+x2sinx1+3x12 κατεληξα σε Vdot=-x22, επιτρεπεται αυτο ?
ναι και εγώ έτσι το πήγα. ότι θέλεις μπορείς να βάλεις στον ελεγκτή λογικά αρκεί να είναι γνωστό.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mitsoschelsea on September 15, 2016, 19:19:29 pm
εγω πηρα ελεγκτη u=-x1-x2+x2sinx1+3x12 κατεληξα σε Vdot=-x22, επιτρεπεται αυτο ?
ναι επιτρέπεται, ότι θέλεις μπορεί να είναι θεωρητικά
Είστε σίγουροι γι' αυτό;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 15, 2016, 19:21:24 pm
ναι αρκεί να τα γνωρίζεις
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Λήσταρχος Γιαγκούλας on September 15, 2016, 19:50:37 pm
Είστε σίγουροι γι' αυτό;
Από την στιγμή που δεν ανφέρεται απαίτηση για γραμμικό ελεγκτήδεν νομίζω να υπάρχει πρόβλημα.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mitsoschelsea on September 15, 2016, 19:58:57 pm
ναι αρκεί να τα γνωρίζεις
Από την στιγμή που δεν ανφέρεται απαίτηση για γραμμικό ελεγκτή
δεν νομίζω να υπάρχει πρόβλημα.
δεν νομίζω να υπάρχει πρόβλημα.
Ευχαριστώ παιδιά.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 15, 2016, 22:50:43 pm
χαζή ερώτηση για τέτοια ώρα αλλά just to be sure, στο θέμα του ιουνίου του 2016 που ζητάει να σχεδιάσουμε ελεγκτή ο οποίος θα καθιστά το 0,0 ολικά ασυμπτωτικά ευσταθές σημείο ισορροπίας, αρχικά για να δείξουμε ότι το 0,0 είναι σημείο ισορροπίας μπορούμε χωρίς πρόβλημα να θεωρήσουμε u = 0 στο σύστημα σωστά;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 15, 2016, 23:06:13 pm
Χρειάζεται να δειξεις αρχικά οτι το μηδεν Σ.Ι ?
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 15, 2016, 23:07:22 pm
Χρειάζεται να δειξεις αρχικά οτι το μηδεν Σ.Ι ?
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
α, το δείχνεις στο τέλος! οκ νο probs! :)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 16, 2016, 00:09:12 am
Χρειάζεται να δειξεις αρχικά οτι το μηδεν Σ.Ι ?
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
Εγώ σχημάτισα εξ.κατ με το u.
Βρηκα V και Vπαραγωγο
ορισα u για να αφαιρεσω
Πηρα Lassalle και μετά εκει που ξαναπηρα τις εξισωσεις καταστασης, έδειξα οτι το (0,0) ειναι μοναδικο Σ.Ι. αρα ολικη ασυμπ ευσταθεια. Είναι λάθος η σειρα;
ναι είναι λάθος, η Lyaponov είναι μόνο για το ΣΙ και μάλιστα αν δεν είναι το (0,0) τότε είναι για z = x - x*
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Schro on September 16, 2016, 00:14:56 am
ναι είναι λάθος, η Lyaponov είναι μόνο για το ΣΙ και μάλιστα αν δεν είναι το (0,0) τότε είναι για z = x - x*
α, ωραία, άρα καλά θυμόμουν ότι πρέπει να το ελέγχουμε!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on September 16, 2016, 00:22:50 am
Αυτό που δεν έχω καταλάβει είναι πότε θεωρούμε u = 0 και πότε βρίσκουμε και το u*
Επίσης σε κάποια για να δείξεις ότι το (0,0) είναι μοναδικό θέλει πολλές πράξεις
Επίσης σε κάποια για να δείξεις ότι το (0,0) είναι μοναδικό θέλει πολλές πράξεις
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 16, 2016, 11:33:01 am
Ποσο βρηκατε στο 2ο θεμα; (Σεπτ 2016)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: kaspas on September 16, 2016, 11:50:08 am
6/c 5/c κατι τετοιο;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: sk0uf on September 16, 2016, 12:15:44 pm
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 16, 2016, 13:11:55 pm
Κρατησατε και τα c? εγω το διαιρεσα στον ελεγκτη. Μετα στο δευτερο ερωτημα κρατησατε το asinx2 και μετα; Εγω πηρα lyapunov, και κατεληξα σε κατι αν θυμαμαι καλα της μορφης -x2^2-x2asinx2, το οποιο ειπα <=0. Πηρα lassalle, και οτι ειναι και μοναδικο το (0,0) οποτε ετσι ειπα ολικη ασυμπ ευσταθεια. Παιζει να ειναι σωστο; :D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Λήσταρχος Γιαγκούλας on September 16, 2016, 13:24:58 pm
Κρατησατε και τα c? εγω το διαιρεσα στον ελεγκτη. Μετα στο δευτερο ερωτημα κρατησατε το asinx2 και μετα; Εγω πηρα lyapunov, και κατεληξα σε κατι αν θυμαμαι καλα της μορφης -x2^2-x2asinx2, το οποιο ειπα <=0. Πηρα lassalle, και οτι ειναι και μοναδικο το (0,0) οποτε ετσι ειπα ολικη ασυμπ ευσταθεια. Παιζει να ειναι σωστο; :D
Ούτε και γω κράτησα το c. 5 και 6Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: csavvidis on September 16, 2016, 14:17:13 pm
Και γω 5 6 βρηκα σωστο? Παιδια στο τελευταιο ποιο σχημα διαλεξατε? Και σε αυτο π ηθελε |χ| να δειξεις φραγμενο με lyapunov και οριακους κυκλους το δειχναμε ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 16, 2016, 14:32:54 pm
Μια επίλυση του /εδιτ Σεπτ2016 θέματος 2 προφανώς το Β συζητιέται τι θα χρησιμοποιήσει ο καθένας
/εδιτ Λόγω αμφιβολιών δικών για την xsin(x) το κατεβάζω για να το ξαναδώ
/εδιτ Λόγω αμφιβολιών δικών για την xsin(x) το κατεβάζω για να το ξαναδώ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: johny93 on September 16, 2016, 14:39:47 pm
Στο θέμα β) έκανα ακριβώς το ίδιο πράγμα με εσένα δηλαδή για κάποιο λόγο που είχε μπει στο μυαλό ότι x*sin(x)>0 , το οποίο δεν ισχύει :( . Παρόλα αυτά όντως η dV/dx βγαίνει αρνητική όπως και να έχει.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 16, 2016, 14:39:57 pm
Στο ένα το σύστημα είναι :
x1dot=x2
x2dot=-αx2-f(x1)
?
x1dot=x2
x2dot=-αx2-f(x1)
?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 16, 2016, 14:40:41 pm
Στο θέμα β) έκανα ακριβώς το ίδιο πράγμα με εσένα δηλαδή για κάποιο λόγο που είχε μπει στο μυαλό ότι x*sin(x)>0 , το οποίο δεν ισχύει :( . Παρόλα αυτά όντως η dV/dx βγαίνει αρνητική όπως και να έχει.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: johny93 on September 16, 2016, 14:42:28 pm
δεν ξέρω αν μιλάει η μαστούρα της αϋπνίας αλλά οταν πλοτάρω το x*sin(x) στο google παίρνει και αρνητικές τιμές
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 16, 2016, 15:07:56 pm
Εγώ προσωπικά έκανα αυτό στο θέμα 2. Αν είναι σωστό πέρασα, αλλιώς rip
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: sk0uf on September 16, 2016, 15:41:41 pm
Κρατησατε και τα c? εγω το διαιρεσα στον ελεγκτη. Μετα στο δευτερο ερωτημα κρατησατε το asinx2 και μετα; Εγω πηρα lyapunov, και κατεληξα σε κατι αν θυμαμαι καλα της μορφης -x2^2-x2asinx2, το οποιο ειπα <=0. Πηρα lassalle, και οτι ειναι και μοναδικο το (0,0) οποτε ετσι ειπα ολικη ασυμπ ευσταθεια. Παιζει να ειναι σωστο; :D
Σωστα. Το c ειτε το κρατησεις ειτε οχι δεν πειραζει. Καλυτερα αμα το δουμε πρακτικα ειναι να το αφησεις για να εχεις εναν λιγοτερο ορο = κοστος .
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 16, 2016, 16:09:31 pm
Καταλαβα, ναι ετσι οπως τα λες εχεις δικιο. Η λυση πως σας φαινεται; Για κοψιμο; :D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: sk0uf on September 16, 2016, 17:12:58 pm
Καταλαβα, ναι ετσι οπως τα λες εχεις δικιο. Η λυση πως σας φαινεται; Για κοψιμο; :D
Εκανες ενα λαθος ,κατα τα αλλα μου φαινεται ενταξει. Τα k1 και k2 επρεπε να τα διαλεξεις εκ νεου ωστε να ισχυει Lyapunov
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 16, 2016, 17:32:52 pm
Καλα αν ισχυει αυτο το λάθος ανετα κοβει ολο το ερωτημα. Αλλα γιατι να χρειαζεται να παρω εκ νεου k1, k2 ? Αν δεις παιρνω Lyapunov με ενα επι 6 στο x1^2.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: sk0uf on September 16, 2016, 18:21:33 pm
Καλα αν ισχυει αυτο το λάθος ανετα κοβει ολο το ερωτημα. Αλλα γιατι να χρειαζεται να παρω εκ νεου k1, k2 ? Αν δεις παιρνω Lyapunov με ενα επι 6 στο x1^2.
Μπορεί να κάνω και λάθος , καθαρά και μόνο από επειδή εγώ κατάλαβα ότι ζητούσε έναν καινούργιο ελεγκτή το είπα.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 16, 2016, 19:29:57 pm
Σεπτέμβριος θέμα 2
Λοιπόν 2 προτεινόμενες λύσεις για το β. Η μια έχει ένα μη γραμμικό ελεγκτή από ΣΑΕ3 (το έλυσε ένας συνάδελφος) και η δική μου με χρήση της sinc<=1 και της ιδιότητας |α|<|β|=> -|β|<α<|β| .
/εδιτ θέμα 2 β) καθαρή φωτο ->https://www.thmmy.gr/smf/index.php?topic=32998.msg1200179#msg1200179
Λοιπόν 2 προτεινόμενες λύσεις για το β. Η μια έχει ένα μη γραμμικό ελεγκτή από ΣΑΕ3 (το έλυσε ένας συνάδελφος) και η δική μου με χρήση της sinc<=1 και της ιδιότητας |α|<|β|=> -|β|<α<|β| .
/εδιτ θέμα 2 β) καθαρή φωτο ->https://www.thmmy.gr/smf/index.php?topic=32998.msg1200179#msg1200179
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mclaren on September 17, 2016, 13:20:18 pm
στο τελευταιο θεμα βγαινει το σχημα Β επειδη το χαρακτηριστικο πολυωνυμο εχει μιγαδικες ριζες αν κανουμε γραμμικοποιηση?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 17, 2016, 13:55:46 pm
Εγώ εκεί πήρα Lyapunov και η παράγωγος βγηκε θετική. οπότε αστάθεια. Το α δεν είναι οποτε ήμουν αναμεσα στο β και γ. Πήρα το γ διότι ετσι οπως εβλεπα τις κυματομορφες του β μου εκανε πιο πολυ για οριακη ευσταθεια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on September 17, 2016, 13:56:51 pm
Εγώ εκεί πήρα Lyapunov και η παράγωγος βγηκε θετική. οπότε αστάθεια. Το α δεν είναι οποτε ήμουν αναμεσα στο β και γ. Πήρα το γ διότι ετσι οπως εβλεπα τις κυματομορφες του β μου εκανε πιο πολυ για οριακη ευσταθεια.
same hereTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mclaren on September 17, 2016, 14:11:17 pm
ειναι ομως ικανη συνθηκη για ασταθεια το οτι η παραγωγος βγηκε θετικη?Θελω να πω οτι υπαρχουν απειρες lyapunov πως ειμαστε σιγουροι οτι ολων οι παραγωγοι βγαινουν θετικες?Παντως οντως το συστημα βγαινει ασταθες με τις ιδιοτιμες του γραμμικοποιημενου 0,5+0,86ι και 0,5-0,86ι.Μπορει να λεω και βλακειες βεβαια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on September 17, 2016, 14:42:32 pm
Η λύση είναι το Α στο τελευταίο, γιατί το σύστημα ξεκινά από σημείο ισορροπίας οπότε και παραμένει σε αυτό (γι'αυτό φαντάζομαι πιάνει μόνο 1 μονάδα :P )
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on September 17, 2016, 14:51:38 pm
Η λύση είναι το Α στο τελευταίο, γιατί το σύστημα ξεκινά από σημείο ισορροπίας οπότε και παραμένει σε αυτό (γι'αυτό φαντάζομαι πιάνει μόνο 1 μονάδα :P )
το σκεφτηκα αυτο, αλλα το ότι έχουμε ασταθεια δεν παιζει ρολο? Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Chester on September 17, 2016, 15:08:24 pm
midfuck. Παιδιά τα λέμε τον Φλεβάρη πάλι εδώ :D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on September 17, 2016, 15:12:20 pm
το σκεφτηκα αυτο, αλλα το ότι έχουμε ασταθεια δεν παιζει ρολο?
Όχι αν είσαι ακριβώς πάνω στο σημείο ισορροπίας.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: AckermanMik on September 17, 2016, 15:18:49 pm
Θετική Lyapunov δε σημαίνει αστάθεια παίδες.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on January 19, 2017, 16:37:28 pm
Παιδιά καλησπέρα , λύσεις για το Φλεβάρη 2016 υπάρχουν πουθενά; όπως επίσης απορία αν αξίζει να ασχοληθεί κάνεις με θέματα του 2013 και πριν σε στυλ με συναρτήσεις μεταφοράς που έμπαιναν προ ροβιθακη εποχής
Ευχαριστώ
Ευχαριστώ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Kodi on January 19, 2017, 16:46:19 pm
Παιδιά καλησπέρα , λύσεις για το Φλεβάρη 2016 υπάρχουν πουθενά; όπως επίσης απορία αν αξίζει να ασχοληθεί κάνεις με θέματα του 2013 και πριν σε στυλ με συναρτήσεις μεταφοράς που έμπαιναν προ ροβιθακη εποχής
Ευχαριστώ
Ευχαριστώ
δεν έχει νόημα να δεις παλιότερα από Ροβιθάκη γιατί έχει άλλη ύλη και γενικά άλλο στυλ θεμάτων!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Indy on February 06, 2017, 17:44:20 pm
Άρα παλιά θέματα βλέπουμε απ το 14 και μετά;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Αλντεμπαράν on February 06, 2017, 17:47:30 pm
Άρα παλιά θέματα βλέπουμε απ το 14 και μετά;
Ναι, από Ιούνιο 2014.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ANDREAMK on February 06, 2017, 17:48:20 pm
Παιδιά κάτι άλλο που είναι σημαντικό.. Κομπιουτεράκι επιτρέπεται; ΓΙατί με.βοηθάει πολύ σε πράξεις με.πίνακες..
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Kodi on February 06, 2017, 17:51:49 pm
Παιδιά κάτι άλλο που είναι σημαντικό.. Κομπιουτεράκι επιτρέπεται; ΓΙατί με.βοηθάει πολύ σε πράξεις με.πίνακες..
συνήθως δε βάζει αριθμούς και αν θυμάμαι καλά τον Σεπτέμβρη είπε ότι δεν επιτρέπεται, αλλά δεν ξέρω αν ήταν για εκείνη τη φορά.
Πάντως δε νομίζω ότι χρειάζεται κάπου...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Indy on February 06, 2017, 17:53:00 pm
Ναι, από Ιούνιο 2014.
thxTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: heavy melon on February 06, 2017, 17:55:20 pm
Παιδιά κάτι άλλο που είναι σημαντικό.. Κομπιουτεράκι επιτρέπεται; ΓΙατί με.βοηθάει πολύ σε πράξεις με.πίνακες..
αχ...πράξεις...μακάρι να φτάσουμε ποτέ στο σημείο που χρειάζεται πράξεις... :'(
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 20:30:21 pm
Σεπτέμβρη 2016 θέμα 1, τι Lyapunov πρέπει να πάρουμε; Επίσης πως εκλέγω μια συνάρτηση lyapunov, πέρα της κλασικής 1/2 x^2
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 11, 2017, 20:36:08 pm
Σεπτέμβρη 2016 θέμα 1, τι Lyapunov πρέπει να πάρουμε; Επίσης πως εκλέγω μια συνάρτηση lyapunov, πέρα της κλασικής 1/2 x^2
για τον σεπτέμβρη με ολοκλήρωμαTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 20:38:42 pm
για τον σεπτέμβρη με ολοκλήρωμα
Ψήσου να δώσεις και έναν τύπο γιατί δεν έχω δει παρόμοια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 11, 2017, 20:50:29 pm
Ψήσου να δώσεις και έναν τύπο γιατί δεν έχω δει παρόμοια.
περίμενε να το δω να το προσπαθήσω. Απλά θυμάμαι ότι έτσι έβγαινε :DTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Kodi on February 11, 2017, 20:52:25 pm
Ψήσου να δώσεις και έναν τύπο γιατί δεν έχω δει παρόμοια.
Νομίζω αυτή είναι υποψήφια Lyapunov:
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 20:56:35 pm
Νομίζω αυτή είναι υποψήφια Lyapunov:
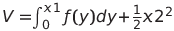
Σωστή μου φαίνεται, απλά η απορία μου ήταν, πως πρέπει να είναι η μορφή μιας συνάρτησης για να είναι lyapunov. Πχ σε διάφορες ασκήσεις που έκανε στην τάξη αυτός πήρε 1-cox1 + 1/2 x2^2 , άλλες έβαλε σταθερές που τις περιόρισε εκεί που βόλευε. Γενικά ποια είναι η συνταγή για να είναι υποψήφια lyapunov? Απλά να περιέχει τις μεταβλητές x1, x2 και δεν μας νοιάζει η μορφή της;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 11, 2017, 21:20:03 pm
Γενικά ποια είναι η συνταγή?
η εμπειρία :Pεδιτ: +1 kodi
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 21:25:48 pm
Kodi και Jason επειδή δεν θυμάμαι ακριβώς πως λες το πρόσημο ολοκληρώματος, αν η προς ολοκλήρωση ποσότητα είναι θετική, λες πως είναι θετικό;
Επίσης στα θέματα επειδή η εξίσωση κατάστασης δεν φαίνεται καλά είναι xdot1=x1 ή =x2 γιατί αν είναι x1 δεν βολεύει νομίζω η συνάρτηση γιατί δεν φεύγουν οι όροι μετά.
Επίσης στα θέματα επειδή η εξίσωση κατάστασης δεν φαίνεται καλά είναι xdot1=x1 ή =x2 γιατί αν είναι x1 δεν βολεύει νομίζω η συνάρτηση γιατί δεν φεύγουν οι όροι μετά.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 11, 2017, 21:36:44 pm
χ2 και φευγουν
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 21:37:48 pm
χ2 και φευγουν
Thx απλά δεν φαινόταν καλά αν είναι 1 ορ 2.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 11, 2017, 21:42:26 pm
Thx απλά δεν φαινόταν καλά αν είναι 1 ορ 2.
έχεις δει μήπως το 5ο θέμα? Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 21:45:16 pm
έχεις δει μήπως το 5ο θέμα?
To είδα, δεν το προσπάθησα. Αλλά υποθέτω βρίσκεις στο περίπου την λύση της διαφορικής;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 11, 2017, 21:48:28 pm
Εγώ προσωπικά έκανα αυτό στο θέμα 2. Αν είναι σωστό πέρασα, αλλιώς rip
Δεν πρέπει να δείχνουμε ότι το σύστημα είναι ελέγξιμο πριν βάλουμε ελεγκτή;;
( επειδή δεν είναι πολύ κατανοητό το quote που κάνω στο παιδί, αναφέρεται στο θέμα 2 σεπ 2016 )
Επίσης όταν θες ελεγκτή που μετακινεί ιδιοτιμές δεν πρέπει να πάρεις και το Kr * r ? Ξέρω πως μόνο το -Kx επιδρά στις ιδιοτιμές, απλά όταν παίρνεις ΓΕΑΚ δεν πρέπει να έχεις και το 2ο κομμάτι του;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 12, 2017, 14:42:36 pm
Επίσης όταν ζητά σημείο ολικά ασυμπτωτικά ευσταθές, απλά εννοεί ότι η απόδειξη ευστάθειας να έχει γίνει δίχως να έχουμε περιοριστεί σε κάποια γειτονιά ή περιοχή;
edit: απάντηση...
edit: απάντηση...
Ναι, άμα αποδείξεις ασυμπτωτική ευστάθεια ενός σημείου και δεν υπάρχει περιορισμός, τότε η ιδιότητα είναι καθολική.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 12, 2017, 15:30:23 pm
Σεπτέμβριος θέμα 2
Λοιπόν 2 προτεινόμενες λύσεις για το β. Η μια έχει ένα μη γραμμικό ελεγκτή από ΣΑΕ3 (το έλυσε ένας συνάδελφος) και η δική μου με χρήση της sinc<=1 και της ιδιότητας |α|<|β|=> -|β|<α<|β| .
Λοιπόν 2 προτεινόμενες λύσεις για το β. Η μια έχει ένα μη γραμμικό ελεγκτή από ΣΑΕ3 (το έλυσε ένας συνάδελφος) και η δική μου με χρήση της sinc<=1 και της ιδιότητας |α|<|β|=> -|β|<α<|β| .
Νομίζω η μία είναι λάθος, καθώς διαίρεσες με x2, πράγμα που εισάγει τον περιορισμό x2 != 0
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Escobar on February 12, 2017, 15:43:28 pm
Επίσης όταν ζητά σημείο ολικά ασυμπτωτικά ευσταθές, απλά εννοεί ότι η απόδειξη ευστάθειας να έχει γίνει δίχως να έχουμε περιοριστεί σε κάποια γειτονιά ή περιοχή;
συνήθως θέλει να αποδείξεις ότι το ΣΙ είναι μοναδικό και άρα έχεις ολική ευστάθεια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 12, 2017, 17:24:25 pm
συνήθως θέλει να αποδείξεις ότι το ΣΙ είναι μοναδικό και άρα έχεις ολική ευστάθεια.
Νομίζω ότι στις σημειώσεις rapunzel το πήρε το μάτι μου κάπου αυτό. Δλδ σε αρκετά σημεία ότι όταν δεν παίρνεις περιορισμό έχεις ολική ευστάθεια σημείου. Αντίθετα αν πχ πω στην γειτονιά του 0 ισχύουν αυτά τότε είναι τοπική ευστάθεια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: matzaris on February 12, 2017, 21:24:18 pm
Θέμα 4 Σεπτ 2016
Τι εννοεί με το "ομοιόμορφα τελικώς φραγμένο";
Για άλλη μια φορά Lyapunov....Τι εννοεί με το "ομοιόμορφα τελικώς φραγμένο";
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on February 13, 2017, 13:40:49 pm
Δεν πρέπει να δείχνουμε ότι το σύστημα είναι ελέγξιμο πριν βάλουμε ελεγκτή;;
( επειδή δεν είναι πολύ κατανοητό το quote που κάνω στο παιδί, αναφέρεται στο θέμα 2 σεπ 2016 )
Επίσης όταν θες ελεγκτή που μετακινεί ιδιοτιμές δεν πρέπει να πάρεις και το Kr * r ? Ξέρω πως μόνο το -Kx επιδρά στις ιδιοτιμές, απλά όταν παίρνεις ΓΕΑΚ δεν πρέπει να έχεις και το 2ο κομμάτι του;
( επειδή δεν είναι πολύ κατανοητό το quote που κάνω στο παιδί, αναφέρεται στο θέμα 2 σεπ 2016 )
Επίσης όταν θες ελεγκτή που μετακινεί ιδιοτιμές δεν πρέπει να πάρεις και το Kr * r ? Ξέρω πως μόνο το -Kx επιδρά στις ιδιοτιμές, απλά όταν παίρνεις ΓΕΑΚ δεν πρέπει να έχεις και το 2ο κομμάτι του;
πως μπορεις να δειξεις οτι ενα συστημα ειναι ελεγξιμο αν ειναι μη γραμμικο? πως θα σχηματισεις τον πινακα Μ? γιατι και για αυτο θα χρησιμοποιησεις τον ελεγκτη σου για να διωξεις τα μη γραμμικα μερη..
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on February 13, 2017, 14:00:54 pm
Νομίζω η μία είναι λάθος, καθώς διαίρεσες με x2, πράγμα που εισάγει τον περιορισμό x2 != 0
μπορείς λίγο να εξηγήσεις τη δεύτερη λύση που προτείνει?
γιατί με lyapunov καταλήγω στο -(x2^2=x2*a*sinx2) και δεν ξερω πως να το αποδειξω οτι αυτο ειναι <=0
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 13, 2017, 14:13:59 pm
μπορείς λίγο να εξηγήσεις τη δεύτερη λύση που προτείνει?
γιατί με lyapunov καταλήγω στο -(x2^2=x2*a*sinx2) και δεν ξερω πως να το αποδειξω οτι αυτο ειναι <=0
γιατί με lyapunov καταλήγω στο -(x2^2=x2*a*sinx2) και δεν ξερω πως να το αποδειξω οτι αυτο ειναι <=0
Αρχικά συμφωνούμε πως είναι λάθος που διαιρεί με x2?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 13, 2017, 14:15:19 pm
πως μπορεις να δειξεις οτι ενα συστημα ειναι ελεγξιμο αν ειναι μη γραμμικο? πως θα σχηματισεις τον πινακα Μ? γιατι και για αυτο θα χρησιμοποιησεις τον ελεγκτη σου για να διωξεις τα μη γραμμικα μερη..
Απλά πως σε μη ελέγξιμο σύστημα παίρνεις ελεγκτή; Δεν ξέρω, λεπτομέρειες ψάχνω γιατί από όσο άκουσα ρίχνει τσεκούρι.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 13, 2017, 18:46:04 pm
Παίζει να χει κανείς λύσεις μαζεμένες για Ιούνιο και Σεπτέμβριο 2016 να ανεβάσει μπας και βγει καμια άκρη? ::) :o
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: heavy melon on February 13, 2017, 20:04:55 pm
Θέματα όπως φλεβάρη 2016, Θέμα 3ο, είναι σωστή η λύση από θέματα που ανέβηκαν απο Αλντεμπαράν;
Γενικά πως σκεφτόμαστε να πάρουμε τον ελεγκτή όταν μας λέει να γραμμ/θεί μέσω ανάδρασης;
στη συγκεκριμένη γιατί θέλουμε να διώξουμε όλους τους όρους κ πότε ξέρουμε αν είναι "ωφέλιμοι"; :???:
Γενικά πως σκεφτόμαστε να πάρουμε τον ελεγκτή όταν μας λέει να γραμμ/θεί μέσω ανάδρασης;
στη συγκεκριμένη γιατί θέλουμε να διώξουμε όλους τους όρους κ πότε ξέρουμε αν είναι "ωφέλιμοι"; :???:
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: 2bleDooR on February 13, 2017, 20:27:49 pm
Παίζει να χει κανείς λύσεις μαζεμένες για Ιούνιο και Σεπτέμβριο 2016 να ανεβάσει μπας και βγει καμια άκρη? ::) :o
χελπ δε γουικ πλιζ γκαιζ ::) :'(
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Escobar on February 13, 2017, 21:29:58 pm
εχεις απολυτο δικιο σε αυτο που λες!!!
βασικα ηθελα να δω σε θεμα οπως αυτο του σεπτεμβριου 2016 θεμα 2 πως μπορω για παραδειγμα να δειξω οτι το συστημα ειναι ελεγξιμο?
κολλαω στο οτι για να το δειξω πρεπει να βρω τον πινακα Μ αρα πρεπει να ξερω τον πινακα Α ,και δεν ξερω πως να ορισω τον Α σε αυτην την περιπτωση
Το απαντάω εδώ για να είναι στο σωστό τόπικ:
Δε θυμάμαι τι είχα γράψει για την ελεγξιμότητα αλλά νομίζω και μία άσκηση που είχε κάνει ο Ροβιθάκης στην τάξη (με μη γραμμικό ελεγκτή, όπως αυτόν που θέλει στο θέμα 2 που λες) δεν είχε μελετήσει καν ελεγξιμότητα. Ίσως θεωρεί ότι είναι δεδομένη
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: jthois on February 14, 2017, 13:31:49 pm
Φεβ.16 Θέμα 2ο
Πως διαχωρίζουμε το σύστημα σε ελέγξιμο και μη ελέγξιμο;
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=32998.0;attach=54059)
Πως διαχωρίζουμε το σύστημα σε ελέγξιμο και μη ελέγξιμο;
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=32998.0;attach=54059)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 14, 2017, 13:43:11 pm
Φεβ.16 Θέμα 2ο
Πως διαχωρίζουμε το σύστημα σε ελέγξιμο και μη ελέγξιμο;
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=32998.0;attach=54059)
Στο Κεφάλαιο 5, εκεί που είναι το Θεώρημα 5.2 και κάτω έχει την εξήγηση. Η λύση είναι στο συννημένο.Πως διαχωρίζουμε το σύστημα σε ελέγξιμο και μη ελέγξιμο;
(https://www.thmmy.gr/smf/index.php?action=dlattach;topic=32998.0;attach=54059)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on February 14, 2017, 14:23:11 pm
υπάρχει καμια λύση του θέματος 1 Σεπτ 2016 ? Γενικά δεν ξερω πως να χρησιμοποιήσω την Lipschitz που δινει
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 14, 2017, 14:24:27 pm
υπάρχει καμια λύση του θέματος 1 Σεπτ 2016 ? Γενικά δεν ξερω πως να χρησιμοποιήσω την Lipschitz που δινει
απο kodi.
Νομίζω αυτή είναι υποψήφια Lyapunov:
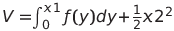
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on February 14, 2017, 21:16:00 pm
Σεπτέμβρης 2016 θέμα 2 β
Τι ορίσατε σαν ελεγκτή και τι σαν lyapunov? Δυσκολευομαι να βγάλω ολικα συμπεράσματα..
Τι ορίσατε σαν ελεγκτή και τι σαν lyapunov? Δυσκολευομαι να βγάλω ολικα συμπεράσματα..
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on February 14, 2017, 21:47:02 pm
Σεπτέμβρης 2016 θέμα 2 β
Τι ορίσατε σαν ελεγκτή και τι σαν lyapunov? Δυσκολευομαι να βγάλω ολικα συμπεράσματα..
Τι ορίσατε σαν ελεγκτή και τι σαν lyapunov? Δυσκολευομαι να βγάλω ολικα συμπεράσματα..
Στο ερώτημα α τι έθεσες σαν ελεγκτή?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on February 14, 2017, 21:57:04 pm
Εγώ προσωπικά έκανα αυτό στο θέμα 2. Αν είναι σωστό πέρασα, αλλιώς rip
Αυτή η λύση είναι σωστή
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on February 14, 2017, 21:59:44 pm
Εμένα δεν μου φαίνεται καθόλου προφανές γιατί η παραγωγός της lyapunov βγαίνει αρνητική εκεί κολλάω
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 14, 2017, 22:00:49 pm
Εμένα δεν μου φαίνεται καθόλου προφανές γιατί η παραγωγός της lyapunov βγαίνει αρνητική εκεί κολλάω
+1
από που και ως που το -ax2sinx2<0
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on February 14, 2017, 22:03:07 pm
Αυτή είναι η λύση μου (Vdot<=0 για |x2|>=2/5 μου ξέφυγε σε εκεινο το σημειο)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: heavy melon on February 15, 2017, 01:44:33 am
ιουνης 2016, θεμα 2, ερωτημα γ) βαζουμε κλασικα ΓΑΚ?
ή ΔΑΚ?
ή ΔΑΚ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 15, 2017, 01:57:27 am
ιουνης 2016, θεμα 2, ερωτημα γ) βαζουμε κλασικα ΓΑΚ?
ή ΔΑΚ?
εγω με ΓΑΚ το ελυσα ή ΔΑΚ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on February 15, 2017, 06:47:27 am
Αυτή είναι η λύση μου (Vdot<=0 για |x2|>=2/5 μου ξέφυγε σε εκεινο το σημειο)
Με Lasalle τοπική ευστάθεια δεν εχουμε? η ασκηση ζηταέι ολικήTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 11:33:22 am
Με Lasalle τοπική ευστάθεια δεν εχουμε? η ασκηση ζηταέι ολική
Ολική νομίζω εκτός και αν εχεις περιορισθει, πχ με γραμμικοποίηση γύρω από το Σ.Ι.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 15, 2017, 11:38:17 am
+1
από που και ως που το -ax2sinx2<0
από που και ως που το -ax2sinx2<0
Άκυρο το προηγούμενο γιατί θα περιόριζες τις τιμές του x2 για τις οποίες ισχύει το αποτελεσμά σου.
--> Όταν x2 ανήκει στο [0,π] (x2>0 ας πούμε) τότε και sinx2>0 και -αx2sinx2<=0
--> Όταν x2 ανήκει στο [0,-π] (x2<0) τότε και sinx2<0 οπότε και πάλι -αx2sinx2<=0
PS.: τα εξηγώ λίγο χαζά αλλά νομίζω βγαίνει νόημα ::)
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on February 15, 2017, 13:41:40 pm
Με Lasalle τοπική ευστάθεια δεν εχουμε? η ασκηση ζηταέι ολική
Ολική είναι με το lasalle
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on February 15, 2017, 13:51:28 pm
Ολική είναι με το lasalle
στις σημειωσεις του τοπικη λεει http://prntscr.com/e8zrloTitle: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: adiaforos on February 15, 2017, 13:57:08 pm
στις σημειωσεις του τοπικη λεει http://prntscr.com/e8zrlo
ειναι αναλογα με το που οριζεται η συναρτηση στις σημειωσεις του η συναρτηση ειναι ορισμενη τοπικα θετικα οπως λεει στις πρωτες δυο σειρες...εξου και το συμπερασμα τοπικο...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ancient on February 15, 2017, 14:01:33 pm
στις σημειωσεις του τοπικη λεει http://prntscr.com/e8zrlo
Αν Ωr=R^n τότε είναι ολικά ασυμπτωτικά ευσταθές.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on February 15, 2017, 14:08:16 pm
Αν Ωr=R^n τότε είναι ολικά ασυμπτωτικά ευσταθές.
ειναι αναλογα με το που οριζεται η συναρτηση
στις σημειωσεις του η συναρτηση ειναι ορισμενη τοπικα θετικα οπως λεει στις πρωτες δυο σειρες...εξου και το συμπερασμα τοπικο...
thanks!στις σημειωσεις του η συναρτηση ειναι ορισμενη τοπικα θετικα οπως λεει στις πρωτες δυο σειρες...εξου και το συμπερασμα τοπικο...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 15:16:52 pm
ειναι αναλογα με το που οριζεται η συναρτηση
στις σημειωσεις του η συναρτηση ειναι ορισμενη τοπικα θετικα οπως λεει στις πρωτες δυο σειρες...εξου και το συμπερασμα τοπικο...
στις σημειωσεις του η συναρτηση ειναι ορισμενη τοπικα θετικα οπως λεει στις πρωτες δυο σειρες...εξου και το συμπερασμα τοπικο...
Τελικά αν δεν πάρω περιορισμό είναι ολικά? Ας το ξεκαθαρισουμε
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on February 15, 2017, 15:23:36 pm
Τελικά αν δεν πάρω περιορισμό είναι ολικά? Ας το ξεκαθαρισουμε
ναι το λεει κ καπου στις χειρογραφες σημειωσεις του 16Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 17:51:33 pm
June 2016, θέμα 2γ , βρήκατε Kr ή το θεωρήσατε 0;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 15, 2017, 17:57:13 pm
June 2016, θέμα 2γ , βρήκατε Kr ή το θεωρήσατε 0;
Μηδέν
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 18:02:51 pm
Μηδέν
Thx, γενικά όταν λέει γραμμική ανάδραση καταστάσεων και γραμμικός ελεγκτής εξόδου για το ίδιο πράγμα μιλάει;
Επίσης στο Lyapunov είναι ανάγκη να του γράφουμε την σφαίρα Br{ } ; Όχι ε;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 15, 2017, 18:18:40 pm
Thx, γενικά όταν λέει γραμμική ανάδραση καταστάσεων και γραμμικός ελεγκτής εξόδου για το ίδιο πράγμα μιλάει;
Επίσης στο Lyapunov είναι ανάγκη να του γράφουμε την σφαίρα Br{ } ; Όχι ε;
Επίσης στο Lyapunov είναι ανάγκη να του γράφουμε την σφαίρα Br{ } ; Όχι ε;
Για το πρώτο νομίζω ότι γραμμικη αναδραση καταστάσεων σου φτάνει u=-k1x1 -k2x2 ενώ ο ελεγκτής εξόδου θα πρέπει να εχει το kr αλλά δεν ξέρω και σίγουρα. Ας πούμε στο θέμα 3 του Ιουνη του 2014 που έλεγε γραμμικό ελεγκτή ανάδρασης καταστάσεων που να διασφαλίζει την ασυμπτωτική σύγκλιση της εξόδου στη λύση παίρνουμε και ελεγκτη με κ, κr και παρατηρητη..οπότε ίσως να χρειαζεται αυτό...αλλά η αλήθεια είναι ότι δεν το έχω πολυκαταλάβει και ελπίζω να μην το βάλει :P O:)
Για το άλλο, όχι δεν χρειάζεται το Br εαν η παράγωγος της V είναι <=0 σε όλο το R^2. Το Βr χρειάζεται όταν είναι <=0 σε υποσύνολο του R^2 οπότε και θα πρέπει να προσδιορίσεις ποιο για την ευστάθεια.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 18:23:07 pm
Για το πρώτο νομίζω ότι γραμμικη αναδραση καταστάσεων σου φτάνει u=-k1x1 -k2x2 ενώ ο ελεγκτής εξόδου θα πρέπει να εχει το kr αλλά δεν ξέρω και σίγουρα.
Για το άλλο, όχι δεν χρειάζεται το Br εαν η παράγωγος της V είναι <=0 σε όλο το R^2. Το Βr χρειάζεται όταν είναι <=0 σε υποσύνολο του R^2 οπότε και θα πρέπει να προσδιορίσεις ποιο για την ευστάθεια.
Για το άλλο, όχι δεν χρειάζεται το Br εαν η παράγωγος της V είναι <=0 σε όλο το R^2. Το Βr χρειάζεται όταν είναι <=0 σε υποσύνολο του R^2 οπότε και θα πρέπει να προσδιορίσεις ποιο για την ευστάθεια.
Τhx... Πάντως εγώ σε κάθε περίπτωση απλού ελεγκτή το κάνω xdot=[Α-ΒK]x δεν είναι να υποθέσω λάθος; Τώρα βλακείες ρωτώ, απλά δεν ξέρω με τον συγκεκριμένο τι μπορεί να τον χαλάσει και να κόψει 1-2 μονάδες.
Γιατί να βάλουμε παρατηρητή; Δεν αρκεί να πεις u=-Kx + Kr * r όπου r η επιθυμητή τιμή που θέλουμε να φέρουμε την έξοδο; Και υπολογισμός του Kr = -1 / (C(A-BK)^-1*B))
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iason1907 on February 15, 2017, 18:24:58 pm
Νομίζω άμα πεις πως έφτασες εκεί (και δεν ζητάει κάτι όπως είπε η Ολγα) δεν θα έχεις θέμα
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 15, 2017, 18:27:12 pm
Τhx... Πάντως εγώ σε κάθε περίπτωση απλού ελεγκτή το κάνω xdot=[Α-ΒK]x δεν είναι να υποθέσω λάθος; Τώρα βλακείες ρωτώ, απλά δεν ξέρω με τον συγκεκριμένο τι μπορεί να τον χαλάσει και να κόψει 1-2 μονάδες.
Γιατί να βάλουμε παρατηρητή; Δεν αρκεί να πεις u=-Kx + Kr * r όπου r η επιθυμητή τιμή που θέλουμε να φέρουμε την έξοδο; Και υπολογισμός του Kr = -1 / (B(A-BK)^-1*C))
Γιατί να βάλουμε παρατηρητή; Δεν αρκεί να πεις u=-Kx + Kr * r όπου r η επιθυμητή τιμή που θέλουμε να φέρουμε την έξοδο; Και υπολογισμός του Kr = -1 / (B(A-BK)^-1*C))
Κοιτα και γω απλά αυτό θα έγραφα... και θα έλεγα ότι είναι το σύστημα κλειστού βρόχου.
Για το 2ο δεν έχω ιδέα γιατί... αλλά η λύση είναι από ένα φίλο που έγραψε 10 τον ιούνη οπότε εμπιστευόμαστε :P
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 18:28:39 pm
Κοιτα και γω απλά αυτό θα έγραφα... και θα έλεγα ότι είναι το σύστημα κλειστού βρόχου.
Για το 2ο δεν έχω ιδέα γιατί... αλλά η λύση είναι από ένα φίλο που έγραψε 10 τον ιούνη οπότε εμπιστευόμαστε :P
Για το 2ο δεν έχω ιδέα γιατί... αλλά η λύση είναι από ένα φίλο που έγραψε 10 τον ιούνη οπότε εμπιστευόμαστε :P
Ιούνιο δυστυχώς για εμάς που δεν το δώσαμε τότε, νομίζω είναι ότι πιο εύκολα θέματα έβαλε ο Ρόβι ως τώρα (μιας που ασχολήθηκα με όλα όσα έχει βάλει πλην προόδων). Θεωρητικά τον εμπιστευόμαστε αλλά δεν μου κάθετε να πάρω παρατηρητή ρε γαμώτο...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: olgatsim on February 15, 2017, 18:32:37 pm
Ιούνιο δυστυχώς για εμάς που δεν το δώσαμε τότε, νομίζω είναι ότι πιο εύκολα θέματα έβαλε ο Ρόβι ως τώρα (μιας που ασχολήθηκα με όλα όσα έχει βάλει πλην προόδων). Θεωρητικά τον εμπιστευόμαστε αλλά δεν μου κάθετε να πάρω παρατηρητή ρε γαμώτο...
Μακάρι να ήξερα να σου απαντήσω τι και πως... :-\
Για τον ελεγκτη u=-k1x1-k2x2 μπορείς αντι να γράψεις κατ'ευθείαν x'=(A-BK)x να πάρεις το αρχικό σύστημα x'=Ax+Bu, να αντικαταστήσεις το u και να κάνεις τον επιμερισμό. Οπότε του δείχνεις και πως το έβγαλες :) :P
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: geralt on February 15, 2017, 18:49:17 pm
Βασικά γραμμικός ελεγκτής ανάδρασης καταστάσεων - > u=-kx+Kr * r
Ελεγκτής ανάδρασης εξόδου έχει και παρατηρητή.
Απλός ελεγκτής γραμμικός ή μη είναι ο u=-kx . Αυτά καταλαβαίνω.
Ελεγκτής ανάδρασης εξόδου έχει και παρατηρητή.
Απλός ελεγκτής γραμμικός ή μη είναι ο u=-kx . Αυτά καταλαβαίνω.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: tpt on June 03, 2017, 22:32:19 pm
εχω την εξής ερώτηση : οταν δίνεται απο την ασκηση οτι μια παράμετρος είναι σταθερη αλλα άγνωστη μπορούμε να ΄βαλουμε στον ελεγκτη την παραμετρο αυτή;Πιο συγκεκριμένα ασκηση 2 θεματα σεπτεμβριος 2016 ερώτημα Β;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 03, 2017, 22:46:45 pm
εχω την εξής ερώτηση : οταν δίνεται απο την ασκηση οτι μια παράμετρος είναι σταθερη αλλα άγνωστη μπορούμε να ΄βαλουμε στον ελεγκτη την παραμετρο αυτή;Πιο συγκεκριμένα ασκηση 2 θεματα σεπτεμβριος 2016 ερώτημα Β;
Σύμφωνα με τον Ρόβυ, αν θυμάμαι καλά, ΓΙΑ ΚΑΝΕΝΑΝ ΠΟΥΣΤΗ ΛΟΓΟ !
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on June 04, 2017, 00:48:46 am
Έλυσε κάνεις το 1ο θέμα, σεπτ 2016 ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 04, 2017, 16:48:11 pm
Για το Θέμα 1 του Σεπτέμβρη 2016
Για το Θέμα 2 του Σεπτέμβρη 2016
Κάποιος πιο παλιά πόσταρε την λύση, την επισύναψα. Δεν νομίζω ότι είναι πλήρως σωστή γιατί δεν δικαιολογεί πως ή V' είναι αρνητικά ημιορισμένη.
Νομίζω αυτή είναι υποψήφια Lyapunov:
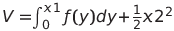
Για το Θέμα 2 του Σεπτέμβρη 2016
Κάποιος πιο παλιά πόσταρε την λύση, την επισύναψα. Δεν νομίζω ότι είναι πλήρως σωστή γιατί δεν δικαιολογεί πως ή V' είναι αρνητικά ημιορισμένη.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on June 04, 2017, 19:32:43 pm
Για το Θέμα 1 του Σεπτέμβρη 2016
Για το Θέμα 2 του Σεπτέμβρη 2016
Κάποιος πιο παλιά πόσταρε την λύση, την επισύναψα. Δεν νομίζω ότι είναι πλήρως σωστή γιατί δεν δικαιολογεί πως ή V' είναι αρνητικά ημιορισμένη.
Για το 1, μάλλον βγαίνει με αυτή τη Lyapunov. Αν το έκανα σωστά, φεύγει η f(x1) η οποία προκύπτει απο την παραγώγιση της V και καταλήγουμε σε V' = -aX22<= 0 και μετά τα γνωστά με Lasalle. Για το Θέμα 2 του Σεπτέμβρη 2016
Κάποιος πιο παλιά πόσταρε την λύση, την επισύναψα. Δεν νομίζω ότι είναι πλήρως σωστή γιατί δεν δικαιολογεί πως ή V' είναι αρνητικά ημιορισμένη.
Για το 2 καταλήγει στο V' = - 5x22 - ax2sin(x2) όπου a = (0,2] και sin(x) = [-1,1] οπότε ο πολλαπλασιασμός δε θα μου δώσει μεγαλύτερο από 5.
Αρα 5x22 > ax2sin(x2) επομένως και αρνητικό να δίνει το ημίτονο η V` θα ειναι πάντα <=0. νομίζω αυτή είναι η λογική.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: tpt on June 04, 2017, 21:54:44 pm
1o θεμα ιουνιου 2016 τι εννοει γραμμικος συνδυασμος?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: bacilis22 on June 05, 2017, 01:33:38 am
έχει λύσει κανείς το θέμα 3 από Φλεβάρη 2016;; Αν ναι γίνεται να το ανεβάσει;;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: paul on June 05, 2017, 12:47:43 pm
Για το 1, μάλλον βγαίνει με αυτή τη Lyapunov. Αν το έκανα σωστά, φεύγει η f(x1) η οποία προκύπτει απο την παραγώγιση της V και καταλήγουμε σε V' = -aX22<= 0 και μετά τα γνωστά με Lasalle.
Μπορεις να ποσταρεις την λυση γιατι εμενα δεν μου βγαινει αυτο που λες...?
Επισης θεωρω πως η συγκεκριμενη Lyapunov δεν ειναι σωστη καθως δεν ξερουμε αν ειναι θετικα ορισμενη. Υπαρχει ασαφεια ως προς το προσημο του ολοκληρωματος. Νομιζω πως θα ηταν σωστη αν μεσα στο ολοκληρωμα ειχαμε yf(y).
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 05, 2017, 14:25:34 pm
Μπορεις να ποσταρεις την λυση γιατι εμενα δεν μου βγαινει αυτο που λες...?
Επισης θεωρω πως η συγκεκριμενη Lyapunov δεν ειναι σωστη καθως δεν ξερουμε αν ειναι θετικα ορισμενη. Υπαρχει ασαφεια ως προς το προσημο του ολοκληρωματος. Νομιζω πως θα ηταν σωστη αν μεσα στο ολοκληρωμα ειχαμε yf(y).
Επισης θεωρω πως η συγκεκριμενη Lyapunov δεν ειναι σωστη καθως δεν ξερουμε αν ειναι θετικα ορισμενη. Υπαρχει ασαφεια ως προς το προσημο του ολοκληρωματος. Νομιζω πως θα ηταν σωστη αν μεσα στο ολοκληρωμα ειχαμε yf(y).
Μάλλον παίρνεις το ολοκλήρωμα για x1 ε [0,c] άρα y>0 => f(y)y>0 => f(y)>0 => oλοκλήρωμα από 0-x1 της f(y)dy θετικά ορισμένο...
Δηλαδή θα καταλήξεις σε τοπική ευστάθεια, όχι ολική...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: paul on June 05, 2017, 15:03:12 pm
Μάλλον παίρνεις το ολοκλήρωμα για x1 ε [0,c] άρα y>0 => f(y)y>0 => f(y)>0 => oλοκλήρωμα από 0-x1 της f(y)dy θετικά ορισμένο...
Δηλαδή θα καταλήξεις σε τοπική ευστάθεια, όχι ολική...
Δηλαδή θα καταλήξεις σε τοπική ευστάθεια, όχι ολική...
Κάνοντας αυτά μου προκύπτει
V'= -ax2^2+f(x1)*(1-x2) αρα θέλω 1-χ2<0 => χ2<1
και
V'= -ax2^2-f(x1)*(1+x2) αρα θέλω 1+χ2>0 => χ2>-1
Αρα για το διαστημα -1<χ2<1 εχουμε τοπικα ασυμπτωτικη ευσταθεια.
Μου φαινεται λιγο περιεργο να μην ασχοληθεις με το [-b,0]. Προς το παρον ομως δεν μου ερχεται τιποτα καλυτερο στο μυαλο.
Θα επανελθω
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on June 05, 2017, 15:37:56 pm
Μπορεις να ποσταρεις την λυση γιατι εμενα δεν μου βγαινει αυτο που λες...?
Επισης θεωρω πως η συγκεκριμενη Lyapunov δεν ειναι σωστη καθως δεν ξερουμε αν ειναι θετικα ορισμενη. Υπαρχει ασαφεια ως προς το προσημο του ολοκληρωματος. Νομιζω πως θα ηταν σωστη αν μεσα στο ολοκληρωμα ειχαμε yf(y).
Το ελυσα βασει το παράδειγμα των σημειώσεων part1 σελίδα 35. Δεν ξέρω αν ειναι όντως σωστό γιατί βγαίνει υπερβολικά ευκολα. Επισης θεωρω πως η συγκεκριμενη Lyapunov δεν ειναι σωστη καθως δεν ξερουμε αν ειναι θετικα ορισμενη. Υπαρχει ασαφεια ως προς το προσημο του ολοκληρωματος. Νομιζω πως θα ηταν σωστη αν μεσα στο ολοκληρωμα ειχαμε yf(y).
edit: μπορει να χρειάζεραι να πουμε κ αυτό
Μάλλον παίρνεις το ολοκλήρωμα για x1 ε [0,c] άρα y>0 => f(y)y>0 => f(y)>0 => oλοκλήρωμα από 0-x1 της f(y)dy θετικά ορισμένο...
Δηλαδή θα καταλήξεις σε τοπική ευστάθεια, όχι ολική...
Δηλαδή θα καταλήξεις σε τοπική ευστάθεια, όχι ολική...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: paul on June 05, 2017, 16:29:07 pm
Νομιζω οτι τελικα και με διερευνηση στο διαστημα (-b,0) στο ιδιο ακριβως συμπερασμα θα καταληξουμε και η Lyapunov θα ειναι θετικη.
Καντε ενα τσεκ αν θελετε για την f(x)=x ή την f(x)=x^3 και θα το καταλαβετε
Καντε ενα τσεκ αν θελετε για την f(x)=x ή την f(x)=x^3 και θα το καταλαβετε
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Austria on June 05, 2017, 20:08:15 pm
Βασικά επειδή είναι ΠΑΡΑ πολλά τα pages αν μπορεί κάποιος να μαζέψει τις ανεβασμένες λύσεις ώστε να μπορούμε να τις σχολιάζουμε πιο εύκολα... Το λέω βασικά μήπως κάποιος που έχει ξαναδώσει το μάθημα μήπως το έχει κάνει ήδη..
+1Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 05, 2017, 20:45:09 pm
Ανεβάζω κάποια λυμένα που βρήκα! Αν ο συγγραφέας τους θέλει copyright, ας μου στείλει πμ. Μέχρι τότε τον ευχαριστούμε !
https://mega.nz/#F!PQphFJTS!MSoaRblmIT7IfWVPJgr1Jw (https://mega.nz/#F!PQphFJTS!MSoaRblmIT7IfWVPJgr1Jw)
edit: fix link
https://mega.nz/#F!PQphFJTS!MSoaRblmIT7IfWVPJgr1Jw (https://mega.nz/#F!PQphFJTS!MSoaRblmIT7IfWVPJgr1Jw)
edit: fix link
Εδώ έχει πολλές λυμένες.
Απολαύστε Υπεύθυνα !!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ap.Mor. on June 06, 2017, 18:16:01 pm
Σεπτέμβριος 2016 Θέμα 4 και Θέμα 5,υπάρχουν πουθενά λύσεις τους;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 06, 2017, 19:08:10 pm
1o θεμα ιουνιου 2016 τι εννοει γραμμικος συνδυασμος?
Eννοεί πως η έξοδος y θα είναι της μορφής y=a * x1 + b * x2 δηλαδή C=[a b]
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iliasT on June 06, 2017, 19:27:29 pm
Eννοεί πως η έξοδος y θα είναι της μορφής y=a * x1 + b * x2 δηλαδή C=[a b]
Υπάρχουν πουθενά λύσεις Ιουνίου 2016;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ablaoublas on June 06, 2017, 19:33:33 pm
Σε προηγούμενες σελίδες αυτού του topic όλο και κάτι θα βρεις. Τα θέματα του Ιουνίου 2016 είναι τα πιο εύκολα που έχει βάλει από όσα έχω δει, μακάρι μεθαύριο να πέσουν τέτοια πάλι ;D
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: dimikara on June 06, 2017, 19:41:18 pm
Για το 1, μάλλον βγαίνει με αυτή τη Lyapunov. Αν το έκανα σωστά, φεύγει η f(x1) η οποία προκύπτει απο την παραγώγιση της V και καταλήγουμε σε V' = -aX22<= 0 και μετά τα γνωστά με Lasalle.
Για το 2 καταλήγει στο V' = - 5x22 - ax2sin(x2) όπου a = (0,2] και sin(x) = [-1,1] οπότε ο πολλαπλασιασμός δε θα μου δώσει μεγαλύτερο από 5.
Αρα 5x22 > ax2sin(x2) επομένως και αρνητικό να δίνει το ημίτονο η V` θα ειναι πάντα <=0. νομίζω αυτή είναι η λογική.
Για το 2 καταλήγει στο V' = - 5x22 - ax2sin(x2) όπου a = (0,2] και sin(x) = [-1,1] οπότε ο πολλαπλασιασμός δε θα μου δώσει μεγαλύτερο από 5.
Αρα 5x22 > ax2sin(x2) επομένως και αρνητικό να δίνει το ημίτονο η V` θα ειναι πάντα <=0. νομίζω αυτή είναι η λογική.
Στο 1ο θέμα πως φεύγουν αφού το f(x1) πολλαπλασιάζεται με το x2?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on June 06, 2017, 19:46:29 pm
Στο 1ο θέμα πως φεύγουν αφού το f(x1) πολλαπλασιάζεται με το x2?
αντικατέστησε το x1' και x2' στην V'(x) και κάνε όλες τις πράξεις. Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ori0ngel on June 06, 2017, 20:44:58 pm
Απο Ιουνιο 2016 υπαρχουν λυσεις?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: s0r0n on June 07, 2017, 14:20:16 pm
Ιουνιος 2016 αν το εκανε κανεις,μου βγαινει στο β) οτι α>-4/3 και στο δ) οτι α>-14,αρα τι λεμε στο ε?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: paul on June 07, 2017, 14:45:31 pm
Ιουνιος 2016 αν το εκανε κανεις,μου βγαινει στο β) οτι α>-4/3 και στο δ) οτι α>-14,αρα τι λεμε στο ε?
Εγω θα ελεγα οτι με την εφαρμογη του ελεγκτη παρατηρουμε μεγαλυτερο ευρος στις τιμες του α για τις οποιες το συστημα ειναι ευσταθες.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: dimikara on June 07, 2017, 18:03:48 pm
Παιδιά ξέρει κανείς πως είναι οι λύσεις στα θέματα 3,4 και 5 του Σεπτέμβρη του 16?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: DarkPassenger on June 07, 2017, 18:05:29 pm
Παιδιά ξέρει κανείς πως είναι οι λύσεις στα θέματα 3,4 και 5 του Σεπτέμβρη του 16?
στο 5 είναι το Α διότι ξεκινάει από Σ.Ι. οπότε παραμένει σε αυτό. για τα αλλα δεν ξερω
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iliasT on June 07, 2017, 18:11:26 pm
Ιούνιος 2016 το 3ο θέμα πώς το ξεκινάμε; :P
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Apostolof on June 07, 2017, 18:24:48 pm
Ιούνιος 2016 το 3ο θέμα πώς το ξεκινάμε; :P
Νομίζω παίρνεις
x1=q
x2=q'
Άρα
x1'=x2
x2'=-3x1^2 - x2 sin(x1) + u
Μετά δε ξέρω τι να κάνω :(
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: paul on June 07, 2017, 18:31:51 pm
Νομίζω παίρνεις
x1=q
x2=q'
Άρα
x1'=x2
x2'=-3x1^2 - x2 sin(x1) + u
Μετά δε ξέρω τι να κάνω :(
x1=q
x2=q'
Άρα
x1'=x2
x2'=-3x1^2 - x2 sin(x1) + u
Μετά δε ξέρω τι να κάνω :(
Οριζεις την κλασικη Lyapunov και βλεπεις τι σε συμφερει να ορισεις σαν ελεγκτη.
Προσοχη οτι εδω δεν μπορεις να ορισεις ορθα την Lyapunov γιατι δεν εχεις σημειο ισορροπιας (0,0). Το κανεις μονο για να βρεις τι θα βαλεις σαν εισοδο.
Εγω ορισα u= - kx2 - x1 - x2*sin(x1) + 3*x1^2
Επομένως το αρχικο μου συστημα βγαινει
x1'=x2
x2'=-kx2-x1
Το σημειο ισορροπιας ειναι το (0,0).
Ξαναπαιρνω Lyapunov τωρα (ορθα ορισμενη αυτην την φορα) και βγαζω V'= -kx2^2<=0
Lassale κλπ κλπ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Ap.Mor. on June 07, 2017, 18:53:25 pm
Παιδιά ξέρει κανείς πως είναι οι λύσεις στα θέματα 3,4 και 5 του Σεπτέμβρη του 16?
Το θέμα 3 έχω την εντύπωση ότι το απαντάμε όπως στη σελίδα 29/101 των φετινών σημειώσεων!είναι το μόνο παράδειγμα που μπλέκει γεωμετρική ερμηνεία και είναι κάτα κάποιος τρόπο κοντά στην άσκηση.
Αν κάποιος έχει πάντως σίγουρη λύση!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: s0r0n on June 07, 2017, 20:46:39 pm
Ιουνιος 16,1ο θεμα το β),ελεγξιμο η οχι?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iliasT on June 07, 2017, 20:59:52 pm
Ιουνιος 16,1ο θεμα το β),ελεγξιμο η οχι?
det(M) = 0 άρα όχι.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: kaspas on September 09, 2017, 16:41:41 pm
Μπορεί κανείς να μου πει τι γράφουν οι εξισώσεις του 1ου Θέματος Σεπτ. 2016; Επίσης αν τα έχει λύση κανείς και μπορεί να τα ανεβάσει θα ήταν καλό
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: kokkinos drakos ths zhxal on September 11, 2017, 14:31:11 pm
εχει καποιος τις εξισωσεις του πρωτου θεματος απο σεπτεμρβη '16?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Perasmus on September 11, 2017, 18:44:03 pm
Στο Θέμα 2.β - Σεπτέμβριος 2016 έχω κολλήσει. Υπάρχουν χαμένες μέσα στις άπειρες σελίδες του τόπικ κάποιες λύσεις, αλλά καμία δεν μου μοιάζει τελείως εντάξει.
Αν κάποιος έχει να προτείνει κάτι για την Lyapunov...;;
Αν κάποιος έχει να προτείνει κάτι για την Lyapunov...;;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 11, 2017, 18:51:01 pm
σελίδα
https://www.thmmy.gr/smf/index.php?topic=32998.1140
σελίδα 77 λύση δική μου
ps. εάν δεν βγάζεις τα γράμματα να την ξαναβγάλω
https://www.thmmy.gr/smf/index.php?topic=32998.1140
σελίδα 77 λύση δική μου
ps. εάν δεν βγάζεις τα γράμματα να την ξαναβγάλω
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: iliasT on September 12, 2017, 13:53:44 pm
σελίδα
https://www.thmmy.gr/smf/index.php?topic=32998.1140
σελίδα 77 λύση δική μου
ps. εάν δεν βγάζεις τα γράμματα να την ξαναβγάλω
https://www.thmmy.gr/smf/index.php?topic=32998.1140
σελίδα 77 λύση δική μου
ps. εάν δεν βγάζεις τα γράμματα να την ξαναβγάλω
Αν σου είναι εύκολο θα βοηθούσε γιατί στο pdf με το 2Β είναι δύσκολα τα πράγματα...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Andromedas on September 12, 2017, 15:26:16 pm
Αν σου είναι εύκολο θα βοηθούσε γιατί στο pdf με το 2Β είναι δύσκολα τα πράγματα...
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: s0r0n on September 14, 2017, 21:32:53 pm
Ιουνιος 2016 στο τριτο θεμα,τι ελεγκτη παιρνουμε?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: vag178 on September 14, 2017, 22:01:00 pm
Ιουνιος 2016 στο τριτο θεμα,τι ελεγκτη παιρνουμε?
u=-x1^2*x2 -x1 +3*x1^2+x2*sin(x1)
αυτο βρισκω εγω απο lyapunov
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: asamantas on January 20, 2018, 19:50:22 pm
Φεβρουαριος του 2016 θεμα 3ο εχει κανεις τη λυση; Καπου υπαρχει μια ενδεικτικη αλλα δεν νομιζω να δινει 4 μοναδες μονο αυτο.
Οποιος εχει κατι πιο ολοκληρωμενο ας βοηθησει
Οποιος εχει κατι πιο ολοκληρωμενο ας βοηθησει
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Florence on September 10, 2018, 20:10:20 pm
μπορει καποιος να ανεβασει μια ολοκληρωμενη λυση για το θεμα 2 σεπτεμβριου 16 ερωτημα β? λενε ολοι με LaSalle βγαινει αλλα πως?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: leukosaraphs! on September 10, 2018, 23:43:38 pm
Φεβρουαριος του 2016 θεμα 3ο εχει κανεις τη λυση; Καπου υπαρχει μια ενδεικτικη αλλα δεν νομιζω να δινει 4 μοναδες μονο αυτο.
Οποιος εχει κατι πιο ολοκληρωμενο ας βοηθησει
Οποιος εχει κατι πιο ολοκληρωμενο ας βοηθησει
γενικα αυτο το εχει κανει κι μεσα στην ταξη σαν ασκηση (σελ 52). Οι 4 μοναδες μπορει να βρισκονται στο γεγονος, οτι δεν σου λεει οτι ο πινακας Α ειναι θετικα ορισμενος, ετσι ωστε να μπορεις να πεις με σιγουρια οτι οριζεται ο αντιστροφος του και αρα να καταληξεις στο αποτελεσμα.
αρα να κανεις διερευνηση. Βεβαια αν ο Α δεν αντιστρεφεται δεν μπορεις να κανεις κι πολλα! (βασικα δεν μπορεις να κανεις τιποτα) και λογικα λες οτι δεν γινεται!
μην σε παρω κι στον λαιμο μου ομως!
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: carini3 on September 12, 2018, 18:19:22 pm
Θεματα 1 και 2 Σεπτεμβρης 2016 στο αρχειο με τις λυσεις βρισκει οτι η lyapunov ειναι αρνητικα ημιορισμενη και σταματαει εκει(ενω στο ενα λεει να μελετηθει η ευσταθεια και στο αλλο να αποδειχθει ασυμπτωτικη ευσταθεια) .Κανονικα και στα 2 δεν πρεπει μετα να κανουμε lasalle για να αποδειξουμε ασυμπτωτικη ευσταθεια;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: κύριος Φασόλης on September 12, 2018, 19:34:28 pm
Θεματα 1 και 2 Σεπτεμβρης 2016 στο αρχειο με τις λυσεις βρισκει οτι η lyapunov ειναι αρνητικα ημιορισμενη και σταματαει εκει(ενω στο ενα λεει να μελετηθει η ευσταθεια και στο αλλο να αποδειχθει ασυμπτωτικη ευσταθεια) .Κανονικα και στα 2 δεν πρεπει μετα να κανουμε lasalle για να αποδειξουμε ασυμπτωτικη ευσταθεια;
Ναι. Συγκεκριμενα για το 1ο εγω βρηκα οτι ειναι ασυμπτ. ευσταθες στο (0,0), οχι ολικα λογω του περιορισμου με τα (-b,c) που δινει. Ειδικα στο 2ο θεμα αν δεν πας με LaSalle στην ουσια δε δειχνεις αυτο που σου λεει (εκτος κι αν παρεις τετοια Lyapunov που να σου εξασφαλισει την ασυμπτωτικη ευσταθεια).
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: carini3 on September 12, 2018, 19:41:42 pm
Ναι. Συγκεκριμενα για το 1ο εγω βρηκα οτι ειναι ασυμπτ. ευσταθες στο (0,0), οχι ολικα λογω του περιορισμου με τα (-b,c) που δινει. Ειδικα στο 2ο θεμα αν δεν πας με LaSalle στην ουσια δε δειχνεις αυτο που σου λεει (εκτος κι αν παρεις τετοια Lyapunov που να σου εξασφαλισει την ασυμπτωτικη ευσταθεια).
και εγω τα ιδια βρηκα. ωραιος,ευχαριστω!Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: pesto80 on September 13, 2018, 21:41:47 pm
παιδια κανεις δεν πήγε να δει λύσεις στον γραφείο του ροβι για το θέμα 3 Σεπτέμβριος 16?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ctsompos on May 30, 2019, 17:11:39 pm
4ο θέμα Σεπτέμβριος 2016 ο ισχυρισμός λάθος δεν είναι ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: xristosioan on June 02, 2019, 16:20:47 pm
4ο θέμα Σεπτέμβριος 2016 ο ισχυρισμός λάθος δεν είναι ?
Ναι. Δεν μπορεί να είναι οσοδήποτε μικρό καθώς εξαρτάται από το γ, το οποίο είναι σταθερά, γνωστή μεν, την οποία δεν μπορούμε να ελέγξουμε δε, καθώς δεν έχουμε εξωτερική είσοδο στο σύστημα.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Spiro on June 09, 2019, 03:19:19 am
Ναι. Δεν μπορεί να είναι οσοδήποτε μικρό καθώς εξαρτάται από το γ, το οποίο είναι σταθερά, γνωστή μεν, την οποία δεν μπορούμε να ελέγξουμε δε, καθώς δεν έχουμε εξωτερική είσοδο στο σύστημα.
Αφού η εκφώνηση λέει "δίνεται το σύστημα κλειστού βρόχου", δηλαδή έχω φτάσει σε αυτές τις εξισώσεις κατάστασης ΑΦΟΥ έκλεισα τον βρόχο με ελεγκτή.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: ctsompos on June 09, 2019, 12:47:19 pm
Υπάρχει λύση απο 3ο θέμα Σεπτεμβρίου ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: tuboflo on June 09, 2019, 14:17:22 pm
Υπάρχει λύση απο 3ο θέμα Σεπτεμβρίου ?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: pesto80 on August 20, 2019, 19:49:51 pm
σεπτ16/θεμα 1
το οτι η f είναι συνεχης κατα lipschitz πως αξιοποιειται στην επιλυση της ασκησης;
το οτι η f είναι συνεχης κατα lipschitz πως αξιοποιειται στην επιλυση της ασκησης;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mermaid on August 20, 2019, 21:10:45 pm
Ειναι προϋπόθεση για να μπορείς να χρησιμοποιήσεις το θεώρημα Lyapunov δες στις σημειώσεις καναβουρα σελ 27.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: pesto80 on August 22, 2019, 16:36:57 pm
Eρώτηση τρίχα αλλά επειδή είναι Ροβιθάκης: σεπτ16 θεμα 2. Eπειδή στην ουσία χρειαζεται με τον ελεγκτη να κανουμε 2 δουλειες:
α) να απαλειψουμε τις μη γραμμικοτητες
β) να στειλουμε τις ιδιοτιμες στις επιθυμητες τιμες,
και επειδη όπως είπες και ο leukos στην προηγούμενη σελίδα, ο ρόβι έχει τέτοιο λυμένο παράδειγμα μες την τάξη (σελ 52) ξερετε αν έχει σημασία για τον Ροβι στη βαθμολογηση αν θα βάλουμε τον ελεγκτή όπως τα λυμένα στα downloads (δηλαδή και τις 2 δουλειες ταυτόχρονα) ή αν θα βάλουμε πρώτα ένα u = (απαλοιφή μη γραμμικοτήτων) + v (νεα εισοδος) και μετα με το v να στείλουμε τις ιδιοτιμες στις τιμες που θελουμε;
α) να απαλειψουμε τις μη γραμμικοτητες
β) να στειλουμε τις ιδιοτιμες στις επιθυμητες τιμες,
και επειδη όπως είπες και ο leukos στην προηγούμενη σελίδα, ο ρόβι έχει τέτοιο λυμένο παράδειγμα μες την τάξη (σελ 52) ξερετε αν έχει σημασία για τον Ροβι στη βαθμολογηση αν θα βάλουμε τον ελεγκτή όπως τα λυμένα στα downloads (δηλαδή και τις 2 δουλειες ταυτόχρονα) ή αν θα βάλουμε πρώτα ένα u = (απαλοιφή μη γραμμικοτήτων) + v (νεα εισοδος) και μετα με το v να στείλουμε τις ιδιοτιμες στις τιμες που θελουμε;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Argirios on August 27, 2019, 00:00:23 am
bump
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: pesto80 on August 27, 2019, 12:35:01 pm
???
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: akdimitri on January 21, 2020, 14:12:43 pm
Στο θεμα 2 του Ιουνιου, γινεται να αποδειξεις ευσταθεια στο συστημα χρησιμοποιώντας det(sI-A)? Δηλαδη να μη λαβεις υποψιν τον πινακα Β.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: mpraskafoutas on January 21, 2020, 15:07:37 pm
Στο θεμα 2 του Ιουνιου, γινεται να αποδειξεις ευσταθεια στο συστημα χρησιμοποιώντας det(sI-A)? Δηλαδη να μη λαβεις υποψιν τον πινακα Β.
έτσι βγαίνει. γενικά η είσοδος u δεν παίζει ρόλο στην ευστάθεια, εκτός και αν σου ζητήσει π.χ. να σχεδιάσεις ελεγκτή ώστε το σύστημα να είναι ευσταθές ή για να πληρούνται κάποιες προδιαγραφές. αυτό στο ζητάει στο ερώτημα γ).
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Thunderlord on June 17, 2020, 19:19:14 pm
Έχει δει κανείς μήπως την Πρόοδο του 16;
Ή υπάρχουν λύσεις; Γιατί δεν βρίσκω κάτι
edit: Θα μπορούσε αυτό να είναι λύση για το δεύτερο θέμα; μου φαίνεται πολύ εύκολο έτσι και ανησυχώ
Ή υπάρχουν λύσεις; Γιατί δεν βρίσκω κάτι
edit: Θα μπορούσε αυτό να είναι λύση για το δεύτερο θέμα; μου φαίνεται πολύ εύκολο έτσι και ανησυχώ
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Thunderlord on June 21, 2020, 20:44:48 pm
Σεπτέμβρης, τελευταίο θέμα
Και στις λύσεις που υπάρχουν στα downloads και στη συζήτηση που έχει προηγηθεί στις προηγούμενες καρτέλες, πολλοί υποστηρίζουν πως το σωστό είναι το Α γιατί είναι ΣΙ και εφόσον ξεκινάει το σύστημα από αυτήν την τιμή δεν θα φύγει ποτέ. Για να συμβεί αυτό όμως, αναγκαία συνθήκη δεν είναι η ευστάθεια; Προσπάθησα με πολλές υποψήφιες V αλλά δεν κατάφερα να αποδείξω ότι έχει ευστάθεια και με γραμμικοποίηση οι ιδιοτιμές βγαίνουν και στο Δεξί ημί επίεδο.
Άρα, μήπως είναι το Γ; Ή ακόμα και ασταθές να είναι το σύστημα, αν ξεκινήσει από το ΣΙ και δεν δέχεται εξωτερική δύναμη παραμένει εκεί;
Και στις λύσεις που υπάρχουν στα downloads και στη συζήτηση που έχει προηγηθεί στις προηγούμενες καρτέλες, πολλοί υποστηρίζουν πως το σωστό είναι το Α γιατί είναι ΣΙ και εφόσον ξεκινάει το σύστημα από αυτήν την τιμή δεν θα φύγει ποτέ. Για να συμβεί αυτό όμως, αναγκαία συνθήκη δεν είναι η ευστάθεια; Προσπάθησα με πολλές υποψήφιες V αλλά δεν κατάφερα να αποδείξω ότι έχει ευστάθεια και με γραμμικοποίηση οι ιδιοτιμές βγαίνουν και στο Δεξί ημί επίεδο.
Άρα, μήπως είναι το Γ; Ή ακόμα και ασταθές να είναι το σύστημα, αν ξεκινήσει από το ΣΙ και δεν δέχεται εξωτερική δύναμη παραμένει εκεί;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: leukosaraphs! on June 21, 2020, 20:58:44 pm
Σεπτέμβρης, τελευταίο θέμα
Και στις λύσεις που υπάρχουν στα downloads και στη συζήτηση που έχει προηγηθεί στις προηγούμενες καρτέλες, πολλοί υποστηρίζουν πως το σωστό είναι το Α γιατί είναι ΣΙ και εφόσον ξεκινάει το σύστημα από αυτήν την τιμή δεν θα φύγει ποτέ. Για να συμβεί αυτό όμως, αναγκαία συνθήκη δεν είναι η ευστάθεια; Προσπάθησα με πολλές υποψήφιες V αλλά δεν κατάφερα να αποδείξω ότι έχει ευστάθεια και με γραμμικοποίηση οι ιδιοτιμές βγαίνουν και στο Δεξί ημί επίεδο.
Άρα, μήπως είναι το Γ; Ή ακόμα και ασταθές να είναι το σύστημα, αν ξεκινήσει από το ΣΙ και δεν δέχεται εξωτερική δύναμη παραμένει εκεί;
Και στις λύσεις που υπάρχουν στα downloads και στη συζήτηση που έχει προηγηθεί στις προηγούμενες καρτέλες, πολλοί υποστηρίζουν πως το σωστό είναι το Α γιατί είναι ΣΙ και εφόσον ξεκινάει το σύστημα από αυτήν την τιμή δεν θα φύγει ποτέ. Για να συμβεί αυτό όμως, αναγκαία συνθήκη δεν είναι η ευστάθεια; Προσπάθησα με πολλές υποψήφιες V αλλά δεν κατάφερα να αποδείξω ότι έχει ευστάθεια και με γραμμικοποίηση οι ιδιοτιμές βγαίνουν και στο Δεξί ημί επίεδο.
Άρα, μήπως είναι το Γ; Ή ακόμα και ασταθές να είναι το σύστημα, αν ξεκινήσει από το ΣΙ και δεν δέχεται εξωτερική δύναμη παραμένει εκεί;
Αν δεις και σημειώσεις Κανναβούρα σελ 18.
Quote
Τα σημεία ισορροπίας είναι σημαντικά, επειδή δηλώνουν πώς όταν φτάσει σε αυτά τα σημεία, ... , τότε το σύστημα δεν πρόκειται να μεταβληθεί. Δηλαδή, ισορροπεί στο x*.
Αν κουνηθείς έστω και λίγο, εκεί χρειάζεσαι την ευστάθεια για να ξέρεις ότι θα γυρίσεις πίσω στο σημείο ισορροπίας. Το θέμα είναι πως αν βρεθείς/ξεκινήσεις σε αυτό ΔΕΝ μεταβάλλεσαι/κουνιέσαι.
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Thunderlord on June 21, 2020, 21:24:02 pm
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Arcade on July 07, 2020, 14:35:21 pm
Βοηθήστε με λίγο: στη λύση αυτή λέει ότι το g είναι βαθμωτό. Αυτό πως βγάινει; Επειδή είναι συνάρτηση; Και έστω ότι ισχύει αυτό, αυτό εδώ πως γίνεται να ισχύει;
(https://i.imgur.com/C3E2A1T.png)
Γενικά, πότε ισχύει ότι ο ανάστροφος ισούται με τον κανονικό; Και πότε το μέτρο του ανάστροφου ισούται με το μέτρο του κανονικού;
(https://i.imgur.com/C3E2A1T.png)
Γενικά, πότε ισχύει ότι ο ανάστροφος ισούται με τον κανονικό; Και πότε το μέτρο του ανάστροφου ισούται με το μέτρο του κανονικού;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Μπιγκόνια on July 07, 2020, 14:49:22 pm
Βοηθήστε με λίγο: στη λύση αυτή λέει ότι το g είναι βαθμωτό. Αυτό πως βγάινει; Επειδή είναι συνάρτηση; Και έστω ότι ισχύει αυτό, αυτό εδώ πως γίνεται να ισχύει;
(https://i.imgur.com/C3E2A1T.png)
Γενικά, πότε ισχύει ότι ο ανάστροφος ισούται με τον κανονικό; Και πότε το μέτρο του ανάστροφου ισούται με το μέτρο του κανονικού;
Η λύση είναι σωστή με εξαίρεση το κομμάτι του g βαθμωτό. Τo g δεν μπορεί να είναι βαθμωτό καθώς πρέπει να ισχύει g ε RN ώστε να ικανοποιείται η αρχική εξίσωση. Η ανισότητα gTPx = xTPg ισχύει γιατί PT = P. Όντως είναι βαθμωτό καθώς [1xN][NxN][Nx1] = [1x1].(https://i.imgur.com/C3E2A1T.png)
Γενικά, πότε ισχύει ότι ο ανάστροφος ισούται με τον κανονικό; Και πότε το μέτρο του ανάστροφου ισούται με το μέτρο του κανονικού;
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Nickgian on April 28, 2021, 19:55:53 pm
Ιουνιος 2016 θεμα 2 ερωτημα γ
πως βγαινει το k2 +5 = 13 , k2 + 3k1 + 4 =42?
πως βγαινει το k2 +5 = 13 , k2 + 3k1 + 4 =42?
Title: Re: [ΣΑΕ ΙΙ] Θέματα 2016
Post by: Thunderlord on April 28, 2021, 20:32:34 pm
Ιουνιος 2016 θεμα 2 ερωτημα γ
πως βγαινει το k2 +5 = 13 , k2 + 3k1 + 4 =42?
πως βγαινει το k2 +5 = 13 , k2 + 3k1 + 4 =42?
δεν θυμάμαι το θέμα, αλλά από αυτό που επισυναψες, βλέπω να παίρνει το Χαρακτηριστικό Πολυονυμο και να θέτει τις δύο ρίζες του με -6, -7 οπότε πλέον ξες τι μορφή θα πρέπει να έχει.
sent from mTHMMY (https://play.google.com/store/apps/details?id=gr.thmmy.mthmmy)