Title: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: dim on June 30, 2005, 00:46:38 am
Μην αναζητείτε και μην ανεβάζετε παλιά θέματα και σημειώσεις εδώ.
Χρησιμοποιείστε τον τομέα Downloads που φτιάχτηκε για αυτόν το σκοπό.
Έτσι βοηθάτε στην καλύτερη κατηγοριοποίησή τους
και στην διευκόλυνση της εύρεσής τους.
Για το Λογισμό Ι μπορείτε να βρείτε παλιά θέματα ή να ανεβάσετε νέα εδώ (http://www.thmmy.gr/smf/index.php?action=tpmod;dl=cat28).
Σχόλια ή απορίες πάνω στα παλιά θέματα του Λογισμού Ι μπορούν να διατυπωθούν εδώ (http://www.thmmy.gr/smf/index.php?topic=1687.0).
edit by mod: Σε ότι αφορά τα παλιά θέματα, έγινε μια προσπάθεια διαχωρισμού για αυτό και θα τα βρείτε ανά εξάμηνο στον υποπίνακα πάνω από τα θέματα. Θα παρακαλούσα λοιπόν να σχολιάζεται εκεί (ή και να ανοίξεται καινούρια topic για νεότερες εξεταστικές). Εδώ υπάρχουν μόνο αταξινόμητες συζητήσεις που κατά κύριο λόγο δεν αντιστοιχούνταν σε συγκεκριμένη εξεταστική περίοδο.
Χρησιμοποιείστε τον τομέα Downloads που φτιάχτηκε για αυτόν το σκοπό.
Έτσι βοηθάτε στην καλύτερη κατηγοριοποίησή τους
και στην διευκόλυνση της εύρεσής τους.
Για το Λογισμό Ι μπορείτε να βρείτε παλιά θέματα ή να ανεβάσετε νέα εδώ (http://www.thmmy.gr/smf/index.php?action=tpmod;dl=cat28).
Σχόλια ή απορίες πάνω στα παλιά θέματα του Λογισμού Ι μπορούν να διατυπωθούν εδώ (http://www.thmmy.gr/smf/index.php?topic=1687.0).
edit by mod: Σε ότι αφορά τα παλιά θέματα, έγινε μια προσπάθεια διαχωρισμού για αυτό και θα τα βρείτε ανά εξάμηνο στον υποπίνακα πάνω από τα θέματα. Θα παρακαλούσα λοιπόν να σχολιάζεται εκεί (ή και να ανοίξεται καινούρια topic για νεότερες εξεταστικές). Εδώ υπάρχουν μόνο αταξινόμητες συζητήσεις που κατά κύριο λόγο δεν αντιστοιχούνταν σε συγκεκριμένη εξεταστική περίοδο.
Title: Λογισμός 1 - Παλιά θέματα - Σχολιασμός και απορίες
Post by: dim on June 30, 2005, 00:50:49 am
Εδώ μπορείτε να σχολιάζετε τα θέματα και
να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού Ι.
(Τα παλιά θέματα υπάρχουν στον τομέα Downloads)
να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού Ι.
(Τα παλιά θέματα υπάρχουν στον τομέα Downloads)
Title: Re: Παλιά θέματα
Post by: Alexkasgr on July 01, 2005, 00:49:05 am
Παλιά θέματα, σύντομη θεωρία καθώς και ασκήσεις για λύση (μαζί με τα αποτελέσματά τους) για το μάθημα "Λογισμός Ι" θα βρείτε στη διεύθυνση:
http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45
http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45
Title: Απ: Παλιά θέματα
Post by: fugiFOX on July 01, 2005, 14:47:59 pm
Παλιά θέματα, σύντομη θεωρία καθώς και ασκήσεις για λύση (μαζί με τα αποτελέσματά τους) για το μάθημα "Λογισμός Ι" θα βρείτε στη διεύθυνση:
http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45
Έβαλες το ίδιο λινκ που έγραψε και ο Dim...http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45
Title: Re: Παλιά θέματα
Post by: Alexkasgr on July 01, 2005, 17:04:10 pm
Το ξέρω, απλά πρόσθεσα ότι έχει και θεωρία και ασκήσεις εκτός από τα παλιά θέματα.
Title: Απ: Παλιά θέματα
Post by: Alexkasgr on October 16, 2005, 13:16:33 pm
Ανέβηκαν... φρεσκοσκαναρισμένα παλιά θέματα, Φεβρουαρίου και Σεπτεμβρίου 1995 (Α & Β). ;D
Title: Re: Παλιά θέματα - Σχολιασμός και απορίες
Post by: d0t1st on December 23, 2005, 14:00:16 pm
Εδώ μπορείτε να σχολιάζετε τα θέματα και
να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού Ι.
(Τα παλιά θέματα υπάρχουν εδώ (http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45)).
Object not found!να συζητάτε τις όποιες απορίες σας πάνω σε παλιά θέματα του
Λογισμού Ι.
(Τα παλιά θέματα υπάρχουν εδώ (http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45)).
The requested URL was not found on this server. The link on the referring page seems to be wrong or outdated. Please inform the author of that page about the error.
If you think this is a server error, please contact the webmaster.
Error 404
www.thmmy.gr
Fri Dec 23 13:58:25 2005
Apache
Exw auto to problima an mporite na boi8isete me pm
Title: Re: Παλιά θέματα - Σχολιασμός και απορίες
Post by: Alexkasgr on December 23, 2005, 14:21:45 pm
Παίδες χαλαρώστε, χθες μεταφέρθηκε εδώ το site και τα downloads από ότι φαίνεται δεν ήρθαν ακόμα. Θα είναι στις προτεραιότητες πάντως... :)
Title: Re: Παλιά θέματα
Post by: MARIOS on February 02, 2006, 12:14:52 pm
παιδιά εκτώς από τα θέματα του 95 υπάρχει περίπτωση να βρούμε και άλλων χρώνων?
Title: Απ: Παλιά θέματα
Post by: Alexkasgr on February 02, 2006, 15:14:50 pm
Xλωμό, δεν έχουν κυκλοφορήσει άλλα νομίζω.
Πάντως μην τα υποτιμάτε τα παλιά, παρότι 10+ χρόνια πριν εξακολουθούν να είναι τα στάνταρ θέματα που μπαίνουν στον λογισμό:
Ολοκληρώματα σε πολικές συντεταγμένες, αναπτυγμα Taylor-MacLaurin, ακτίνα σύγκλισης δυναμοσειράς (ειδικά κριτήριο D' Alembert!), παράγωγος πεπλεγμένης συνάρτησης, γενικευμένα ολοκληρώματα και απλά αόριστα ολοκληρώματα που πρέπει να τα παίζετε στα δάχτυλα.
Πάντως μην τα υποτιμάτε τα παλιά, παρότι 10+ χρόνια πριν εξακολουθούν να είναι τα στάνταρ θέματα που μπαίνουν στον λογισμό:
Ολοκληρώματα σε πολικές συντεταγμένες, αναπτυγμα Taylor-MacLaurin, ακτίνα σύγκλισης δυναμοσειράς (ειδικά κριτήριο D' Alembert!), παράγωγος πεπλεγμένης συνάρτησης, γενικευμένα ολοκληρώματα και απλά αόριστα ολοκληρώματα που πρέπει να τα παίζετε στα δάχτυλα.
Title: Απ: Παλιά θέματα
Post by: !!DUO!!(Αγγίζοντας την τελειότητα..) on February 08, 2006, 17:31:46 pm
Παλιά θέματα, σύντομη θεωρία καθώς και ασκήσεις για λύση (μαζί με τα αποτελέσματά τους) για το μάθημα "Λογισμός Ι" θα βρείτε στη διεύθυνση:
http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45 (http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45)
Έβαλες το ίδιο λινκ που έγραψε και ο Dim...http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45 (http://www.thmmy.gr/index.php?option=com_docman&task=cat_view&gid=107&Itemid=45)
Title: Re: Παλιά θέματα
Post by: dim on February 08, 2006, 17:42:42 pm
Μα.......Φυσικά και δεν δουλεύει..!!!! ^sealed^ :P :P :P :P
Προς το παρών.. ;)
Αυτό οφείλεται στην αλλαγή του server που έκαναν οι αντιμινιστράτορες!!
Η μεταφορά του section dowloads δεν έχει γίνει ακόμα..
Κάνε right click πάνω στο link, και αφού σου βγάλει το μνμ ότι δεν υπάρχει η σελίδα κτλ, πήγαινε στη γραμμή διευθύνσεων, και όπου thmmy βάλε smps..!! ;) ;)
Οπότε και θα πας στο "mirror" του foroum που χρησιμοποιούσαμε πριν λίγο καιρό.. ^hello^
απαλό και απλό!
Εκτός αν θες να το κάνεις εντελώς χειροκίνητα, οπότε..πάσο..! 8)
Προς το παρών.. ;)
Αυτό οφείλεται στην αλλαγή του server που έκαναν οι αντιμινιστράτορες!!
Η μεταφορά του section dowloads δεν έχει γίνει ακόμα..
Κάνε right click πάνω στο link, και αφού σου βγάλει το μνμ ότι δεν υπάρχει η σελίδα κτλ, πήγαινε στη γραμμή διευθύνσεων, και όπου thmmy βάλε smps..!! ;) ;)
Οπότε και θα πας στο "mirror" του foroum που χρησιμοποιούσαμε πριν λίγο καιρό.. ^hello^
απαλό και απλό!
Εκτός αν θες να το κάνεις εντελώς χειροκίνητα, οπότε..πάσο..! 8)
Title: Απ: Παλιά θέματα
Post by: asousos on September 18, 2006, 15:07:31 pm
Γεια....
Θα παρακαλούσα όσους έδωσαν πέρυσι το μάθημα(Φεβρουάριος 2006), να γράψουν περίπου/ακριβώς( ::) ) τις ασκησεις που έπεσαν, την διάρθρωση και φιλοσοφία των ερωτημάτων, προσωπικές παρατηρήσεις κλπ συναφή στοιχεία... και γενικότερα το πνεύμα της εξέτασης...
^beg^
Ευχαριστώ εκ των προτέρων...
Υ.Γ.: Συνοπτικά πράγματα... μην χάσετε και πολύ χρόνο... 8)
Θα παρακαλούσα όσους έδωσαν πέρυσι το μάθημα(Φεβρουάριος 2006), να γράψουν περίπου/ακριβώς( ::) ) τις ασκησεις που έπεσαν, την διάρθρωση και φιλοσοφία των ερωτημάτων, προσωπικές παρατηρήσεις κλπ συναφή στοιχεία... και γενικότερα το πνεύμα της εξέτασης...
^beg^
Ευχαριστώ εκ των προτέρων...
Υ.Γ.: Συνοπτικά πράγματα... μην χάσετε και πολύ χρόνο... 8)
Title: Απ: Παλιά θέματα
Post by: Junior on September 18, 2006, 18:17:33 pm
Είναι δύσκολο να θυμηθούμε τα θέματα μετά από 7 μήνες :/
Νομίζω καλύπτονταν πολλά θέματα (ακολουθίες, σειρές, διαφορικά, ολοκληρώματα, αλλαγή μεταβλητής, γενικευμένα κλπ)
Πάντως θυμάμαι σίγουρα ότι έδινε συνολικά 11 μονάδες
Νομίζω καλύπτονταν πολλά θέματα (ακολουθίες, σειρές, διαφορικά, ολοκληρώματα, αλλαγή μεταβλητής, γενικευμένα κλπ)
Πάντως θυμάμαι σίγουρα ότι έδινε συνολικά 11 μονάδες
Title: Re: Παλιά θέματα
Post by: miko on September 23, 2006, 12:17:56 pm
εχω δωσει λογισμο αρκετες φορες κ ξερω πανω κατω που κινειται(με καθε επιφυλαξη) κ συνηθως μπαινουν:α)πεπλεγμενες συναρτησεις β)ολοκληρωματα(παντα!!!!)γ)aylor mclaurin δ)εφαπτομενη ε)μελετη πολικων συντεταγμενων,απεικονιση κ θα ζητησει κ κατι σε εμβαδο απο περιστροφη κτλ.στ)κ μια ασκηση συνηθως με παραμετρικες εξισωσεις.καλη επιτυχια!
Title: Re: Παλιά θέματα
Post by: NetBuster on September 23, 2006, 12:24:58 pm
>>Να προσθεσω οτι βαζει 3 ολοκληρωματα εκ των οποιων τουλαχιστον ενα να το περιμενεις γενικευμενο...
>>Ακομα δωσε βαση στις γραφικες σε πολικο(νομιζω σελιδα 167 - ε ρε τι θυμαμαι 4ετης ανθρωπος) καθως μαλλον θα σου βαλει να σχεδιασεις 2 απο αυτες στο ιδιο Οχy και μετα να βρεις το εμβαδο που περικλειεται απο την τομη τους...Μαθε και τους τυπους εμβαδου στο τελος...(μαθε, λεμε τωρα 8) )
>>+Συγκλιση σειρων...Οχι κατι δυσκολο αλλα θα σου δωσει μια που συνηθως λυνεται με ενα εκ των θεωρηματων(Cauchy κτλ)
>>Ακομα δωσε βαση στις γραφικες σε πολικο(νομιζω σελιδα 167 - ε ρε τι θυμαμαι 4ετης ανθρωπος) καθως μαλλον θα σου βαλει να σχεδιασεις 2 απο αυτες στο ιδιο Οχy και μετα να βρεις το εμβαδο που περικλειεται απο την τομη τους...Μαθε και τους τυπους εμβαδου στο τελος...(μαθε, λεμε τωρα 8) )
>>+Συγκλιση σειρων...Οχι κατι δυσκολο αλλα θα σου δωσει μια που συνηθως λυνεται με ενα εκ των θεωρηματων(Cauchy κτλ)
Title: Re: Παλιά θέματα
Post by: miko on September 23, 2006, 12:33:50 pm
πολυ σωστος!κ εγω 4ο ειμαι κ ακομα το παλευω.
Title: Re: Παλιά θέματα
Post by: ampoulog on August 19, 2007, 11:08:03 am
Μπορούμε σε πολίκες συντεταγμένες να κάνουμε απευθείας αναγνώριση μίας συνάρτησης - σαν γραφική παράσταση-ή πρέπει να κάνουμε και κάποια μελέτη ;
Title: Re: Παλιά θέματα
Post by: hatzf on August 26, 2007, 18:46:17 pm
re pedia lyseis gia ta palia themata yparxoun?
Title: Re: Παλιά θέματα - Σχολιασμός και απορίες
Post by: hatzf on August 26, 2007, 18:47:48 pm
lyseis gia ta palia themata pou mporo na bro?
Title: Re: Παλιά θέματα - Σχολιασμός και απορίες
Post by: Mikros_Nikolas on August 26, 2007, 19:53:16 pm
Έχω μια γενικότερη απορία και νομίζω κολλάει εδώ καθώς συνάντησα προβλήματα στα παλιά θέματα του 94 νομίζω.
Γενικά τα ολοκληρώματα με ρίζες ημίτονων, συνημίτονων και τον συνδυασμών τους λύνονται μόνο με την αντικατάσταση εφ(x/2)=t ή υπάρχει και κανένας άλλος τρόπος;
Όπως καταλάβατε το πρόβλημα το συναντώ όποτε μου ζητείται μήκος και εμβαδόν στερεού εκ περιστροφής από καμπύλες σε πολικές συντεταγμένες.
Γενικά τα ολοκληρώματα με ρίζες ημίτονων, συνημίτονων και τον συνδυασμών τους λύνονται μόνο με την αντικατάσταση εφ(x/2)=t ή υπάρχει και κανένας άλλος τρόπος;
Όπως καταλάβατε το πρόβλημα το συναντώ όποτε μου ζητείται μήκος και εμβαδόν στερεού εκ περιστροφής από καμπύλες σε πολικές συντεταγμένες.
Title: Re: Παλιά θέματα - Σχολιασμός και απορίες
Post by: *** on August 27, 2007, 13:01:57 pm
πολλές φορές μέσα στη ρίζα μπορείς να δημιουργήσεις τετράγωνο χρησιμοποιώντας τριγωνομετρικές ιδιότητες. δες σαν παράδειγμα τη ρίζα
(1+ sinx)^(1/2). η υπόριζη ποσότητα γράφεται 1+sin2(x/2) = 1+ 2sin(x/2)cos(x/2) = (sin(x/2))^2 + (cos(x/2))^2 +2sin(x/2)cos(x/2) = [sin(x/2) + cos(x/2)]^2. οπότε η ρίζα φεύγει. απλώς το να θέσεις εφ(x/2)= t είναι ο κλασικός τρόπος που σου χρησιμεύει στις περισσότερες περιπτώσεις και όταν δεν έχεις έμπνευση να παίξεις με τις σχέσεις
(1+ sinx)^(1/2). η υπόριζη ποσότητα γράφεται 1+sin2(x/2) = 1+ 2sin(x/2)cos(x/2) = (sin(x/2))^2 + (cos(x/2))^2 +2sin(x/2)cos(x/2) = [sin(x/2) + cos(x/2)]^2. οπότε η ρίζα φεύγει. απλώς το να θέσεις εφ(x/2)= t είναι ο κλασικός τρόπος που σου χρησιμεύει στις περισσότερες περιπτώσεις και όταν δεν έχεις έμπνευση να παίξεις με τις σχέσεις
Title: Re: Λογισμός 1 - Σχολιασμός φετινών θεμάτων... (9/07)
Post by: Alexkasgr on August 28, 2007, 20:32:01 pm
Μία άσχετη παρατήρηση:
Μερικοί ίσως το έχετε προσέξει, άλλοι ίσως δεν το ξέρετε. Για σχολιασμό θεμάτων υπάρχουν έτοιμα topics σε κάθε πίνακα μαθημάτων, συγκεκριμένα για το Λογισμό Ι είναι το:
http://www.thmmy.gr/smf/index.php?topic=1687.0
Βέβαια μπορείτε να... ξεθυμάνετε εδώ και απλά να τα συγχωνεύσουμε μετά, για να είναι όλοι οι σχολιασμοί θεμάτων σε ένα topic. Αν κάποιος θυμάται ή αντέγραψε κάπως τα θέματα, καλό θα ήταν να τα ανεβάσει στα Downloads για να βοηθήσει μελλοντικά και άλλους συμφοιτητές μας (αλλά και για να καταλαβαίνει ο κόσμος μετά για τι πράγμα μιλάτε!).
Πάντως φαίνεται να έχετε ένα μειονέκτημα ότι δεν πήρατε μέσα στη χρονιά το βάπτισμα του πυρός από εξετάσεις και πρέπει να το αντιμετωπίσετε με ψυχραιμία!
Μερικοί ίσως το έχετε προσέξει, άλλοι ίσως δεν το ξέρετε. Για σχολιασμό θεμάτων υπάρχουν έτοιμα topics σε κάθε πίνακα μαθημάτων, συγκεκριμένα για το Λογισμό Ι είναι το:
http://www.thmmy.gr/smf/index.php?topic=1687.0
Βέβαια μπορείτε να... ξεθυμάνετε εδώ και απλά να τα συγχωνεύσουμε μετά, για να είναι όλοι οι σχολιασμοί θεμάτων σε ένα topic. Αν κάποιος θυμάται ή αντέγραψε κάπως τα θέματα, καλό θα ήταν να τα ανεβάσει στα Downloads για να βοηθήσει μελλοντικά και άλλους συμφοιτητές μας (αλλά και για να καταλαβαίνει ο κόσμος μετά για τι πράγμα μιλάτε!).
Πάντως φαίνεται να έχετε ένα μειονέκτημα ότι δεν πήρατε μέσα στη χρονιά το βάπτισμα του πυρός από εξετάσεις και πρέπει να το αντιμετωπίσετε με ψυχραιμία!
Title: Re: Λογισμός 1 - Παλιά θέματα - Σχολιασμός και απορίες
Post by: Itachi on February 01, 2008, 13:34:37 pm
Ο Ξενος σε ενα μαθημα θυμαμαι οτι ειπε πως δεν χρειαζεται να μαθουμε απ'εξω ολους τους τυπους του βιβλιου για τα ολοκληρωματα...Δινουν μηπως καποιο τυπολογιο η απλα πρεπει να ξερουμε να βγαζουμε τους τυπους απο μονοι μας? Ειναι καπως αδυνατον βεβαια να θυμαται κανεις τοσους τυπους....
Title: Re: Λογισμός 1 - Παλιά θέματα - Σχολιασμός και απορίες
Post by: ampoulog on February 01, 2008, 13:48:59 pm
Πρέπει να ξέρεις να βγάζεις τους τύπους απο μόνο σου .
Τουλάχιστον πέρυσι δεν έδωσαν τυπολόγιο .
Οι τύποι που χρειάζονται περισσότερο είναι αυτοί στα εμβαδα και στους όγκους και να ξέρεις για καρτεσιανές συντεταγμένες τότε μπορείς εύκολα να βγάλεις και τους υπόλοιπους .
Τουλάχιστον πέρυσι δεν έδωσαν τυπολόγιο .
Οι τύποι που χρειάζονται περισσότερο είναι αυτοί στα εμβαδα και στους όγκους και να ξέρεις για καρτεσιανές συντεταγμένες τότε μπορείς εύκολα να βγάλεις και τους υπόλοιπους .
Title: Re: Λογισμός 1 - Παλιά θέματα - Σχολιασμός και απορίες
Post by: Itachi on February 01, 2008, 15:01:19 pm
Thnx...Το να ξερεις να τους βγαζεις ειναι ευκολο...Το να τους μαθεις απ'εξω ειναι το αδυνατο...Απ'οτι ειδα βεβαια σε εμας οι ογκοι ειναι εκτος υλης.... ;D ;D Αλλα απο την αλλη θα μου πει κανεις σιγα μη δωσει τυπολογιο ο Ροθος...
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: ampoulog on February 01, 2008, 16:15:41 pm
Εμείς πέρυσι δεν είχαμε Ρούθο είχαμε Ξένο και μία γυναίκα (δεν θυμάμαι το ονομά της).
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Laharl on January 13, 2010, 17:27:21 pm
Παίδες να ρωτήσω
Υπάρχουν και άλλα παλαιότερα θέματα πουθενά πέραν αυτών στον τομέα Downloads?
Όχι μόνον για τον Λογισμό αλλά και για τα άλλα μαθήματα
Ευχαριστώ πολύ :)
Υπάρχουν και άλλα παλαιότερα θέματα πουθενά πέραν αυτών στον τομέα Downloads?
Όχι μόνον για τον Λογισμό αλλά και για τα άλλα μαθήματα
Ευχαριστώ πολύ :)
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: raf on January 13, 2010, 20:57:30 pm
Mπές στο site http://users.auth.gr/~valexiad/ ;)
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: makhs on January 29, 2010, 16:45:17 pm
μηπως μπορει να μου πει καποιος ποια ειναι η υλη..?? και ποιες ειναι οι σελιδες στο βιβλιο του Ξενου????
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: il capitano on January 29, 2010, 16:47:26 pm
μπορεις να πας σε κανενα τοπικ παραδιπλα και να δεις ;)
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: di_em on August 29, 2010, 15:50:45 pm
Θύμαται κανείς τι διάγραμμα ζητούσε ο κ. Ξένος στο 4ο Θέμα τον προηγούμενο Φεβρουάριο?
Title: Re: [Λογισμός 1] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Tracy_McGrady on August 29, 2010, 16:41:04 pm
Θύμαται κανείς τι διάγραμμα ζητούσε ο κ. Ξένος στο 4ο Θέμα τον προηγούμενο Φεβρουάριο?
Αν δεν κάνω μεγάλο λάθος ζητούσε γραφική 2 συναρτήσεων πολικών συντεταγμένων σε κοινό διάγραμμα!..και μετά κάτι με τουσ τύπους!Να ρωτήσω και εγω τωρα...θυμάστε αν δίπλα στους τύπους έγραφε και αν είναι π.χ. μήκος τόξου καμπύλης κλπ???Η πρέπει να ξέρουμε ποιός τυπος είναι τι???
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Silvershot on February 06, 2011, 20:01:39 pm
πως βρισκω αν η σειρα της εικονας συγκλινει?
http://dl.dropbox.com/u/9693610/photos/seira.jpg
http://dl.dropbox.com/u/9693610/photos/seira.jpg
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Godhatesusall on February 06, 2011, 22:30:04 pm
πως βρισκω αν η σειρα της εικονας συγκλινει?
http://dl.dropbox.com/u/9693610/photos/seira.jpg
http://dl.dropbox.com/u/9693610/photos/seira.jpg
Πάρε την n-οστή ρίζα του an. Άρα τώρα θα έχεις
|ν-οστή ρίζα{ ( n/n+1)^n} * ν-οστή ρίζα{ ( n/n+1)^n}|= n/(n+1) * n/(n+1). Και επειδή n/(n+1) <1 , συγκλίνει
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: whitesnake_92 on February 06, 2011, 22:46:54 pm
πως βρισκω αν η σειρα της εικονας συγκλινει?
http://dl.dropbox.com/u/9693610/photos/seira.jpg
http://dl.dropbox.com/u/9693610/photos/seira.jpg
Πάρε την n-οστή ρίζα του an. Άρα τώρα θα έχεις
|ν-οστή ρίζα{ ( n/n+1)^n} * ν-οστή ρίζα{ ( n/n+1)^n}|= n/(n+1) * n/(n+1). Και επειδή n/(n+1) <1 , συγκλίνει
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Silvershot on February 06, 2011, 23:51:59 pm
πως βρισκω αν η σειρα της εικονας συγκλινει?
http://dl.dropbox.com/u/9693610/photos/seira.jpg
http://dl.dropbox.com/u/9693610/photos/seira.jpg
Πάρε την n-οστή ρίζα του an. Άρα τώρα θα έχεις
|ν-οστή ρίζα{ ( n/n+1)^n} * ν-οστή ρίζα{ ( n/n+1)^n}|= n/(n+1) * n/(n+1). Και επειδή n/(n+1) <1 , συγκλίνει
ναι ακριβως. σε παραπεμπει να παρεις ριζα αλλα καταληγεις το lim=1 αρα δε μπορεις να συμπερανεις. Προφανως καπως αλλιως γινεται..
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Burlitsa on February 07, 2011, 00:29:05 am
βασικά ένας φίλος μου πε οτι λύνεται ως εξής (αλλά εμένα δεν μου στέκει η απαλοιφή στην ρίζα..)

Ισχύει σίγουρα ότι
 λάθος =
λάθος = 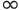

Ισχύει σίγουρα ότι
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: png on February 07, 2011, 00:35:12 am
με κοινή λογική 1 δεν κάνει αυτό;
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on February 07, 2011, 00:39:06 am
Ισχύει σίγουρα ότι

(http://cdn3.knowyourmeme.com/i/000/082/175/original/girls_laughing.jpg?1289453764)oxi
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Orfikoss on February 07, 2011, 00:40:23 am
Ισχύει σίγουρα ότι

Είναι
Και αυτό διότι
Edit: Μάλλον θες να πεις ότι
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: zisis00 on February 07, 2011, 00:41:04 am
αυτο μπορεις να μου το εξηγήσεις πως ακριβώς το κάνεις ?
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: zisis00 on February 07, 2011, 00:44:22 am
Επίσης να και κάτι παράξενο...
Code:
http://www.wolframalpha.com/input/?i=sum+%28n%2F%28n%2B1%29%29^%28n^2%29
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Burlitsa on February 07, 2011, 00:51:43 am
wtf???? 1/e<1 άρα συγκλίνει
e=2.7$#%@$%#@$
e=2.7$#%@$%#@$
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Burlitsa on February 07, 2011, 00:55:59 am
:o :o :o :o :o :o
πότε γράφηκε αυτή η σελ και δεν τι πήρα μυρουδιά?
άπλυτε οφείλω να ομολογήσω οτι για το
πρώτο λιμ απλά άκουσα αυτο που είπε ο φίλος
το 2ο το βρήκα στο βιβλίο....
πότε γράφηκε αυτή η σελ και δεν τι πήρα μυρουδιά?
άπλυτε οφείλω να ομολογήσω οτι για το
πρώτο λιμ απλά άκουσα αυτο που είπε ο φίλος
το 2ο το βρήκα στο βιβλίο....
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Burlitsa on February 07, 2011, 01:11:00 am
καποιος να απαντησει στη σειρα πως την βρισκουμε εφοσον ολοι οι τροποι οδηγουν στη ....καταστοφη :o :o :o :-X
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Silvershot on February 07, 2011, 01:29:24 am
βασικά ένας φίλος μου πε οτι λύνεται ως εξής (αλλά εμένα δεν μου στέκει η απαλοιφή στην ρίζα..)

Ισχύει σίγουρα ότι

Ισχύει σίγουρα ότι
πραγματικα πως φευγει το ^2 με τη νιοστη ριζα? Επισης ειναι λαθος το κλασμα υψομενο στην n και μετα στο τετραγωνο. Einai n*n oxi 2n, πως γινεται?! Μην αλλαξουμε και τα μαθηματικα που ξεραμε 8))
Τεσπα εγω τι κανω καλη επιτυχια σε οσους δινουν αυριο!
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Orfikoss on February 07, 2011, 11:32:54 am
Θέλουμε να εξετάσουμε αν η  συγκλίνει
συγκλίνει
Αν αρκεί νδο
αρκεί νδο 
Είναι:



Θα εξετάσουμε κάθε όρο ξεχωριστά.


και


Άρα
Αν
Είναι:
Θα εξετάσουμε κάθε όρο ξεχωριστά.
και
Άρα
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Silvershot on February 07, 2011, 15:04:16 pm
Και να φανταστεις το πηρα με τη φαντασια! Δεν ηξερα πως βγαινει κανονικα. παλι καλα ημουν τυχερος..
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: takzago on June 15, 2011, 10:11:23 am
Καλημέρα!
Μήπως έχει κανείς παλιά θέματα του Ρόθου να ανεβάσει, εκτός βέβαια από αυτά που έχει στα downloads?
Θέλω να το δώσω τώρα ποτυχιακή και θα εκτιμούσα πολύ όποιον βοηθούσε!
Μήπως έχει κανείς παλιά θέματα του Ρόθου να ανεβάσει, εκτός βέβαια από αυτά που έχει στα downloads?
Θέλω να το δώσω τώρα ποτυχιακή και θα εκτιμούσα πολύ όποιον βοηθούσε!
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: pentium4 on June 15, 2011, 22:05:26 pm
τσέκαρε στις ελεύθερες σημειώσεις στη βιβλιοθήκη ηλεκτρολόγων..
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: takzago on June 17, 2011, 11:06:45 am
Δυστυχώς δεν έχει τίποτα!
Μήπως έχει κανείς θέματα του Ρόθου ή σημειώσεις από το μάθημά του?
Σας παρακαλώ, αν μπορείτε βοηθήστε.
Μήπως έχει κανείς θέματα του Ρόθου ή σημειώσεις από το μάθημά του?
Σας παρακαλώ, αν μπορείτε βοηθήστε.
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on June 17, 2011, 20:27:15 pm
αν θες τις εργασιες που εβαζε προς βαθμολογια στο 1ο εξαμηνο,ειναι στο ethmmy..και επισυναπτω μερικα και εδω..δες αμα βοηθανε καθολου
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: takzago on June 18, 2011, 00:31:05 am
Σε ευχαριστώ πολύ!
Μήπως μπορεί κάποιος που έκανε τις εργασίες να τις ποστάρει εδώ?
Ειδικά στις ακολουθίες έχω πρόβλημα και θέλω ένα μπούσουλα για να κάνω καμιά άσκηση...
Μήπως μπορεί κάποιος που έκανε τις εργασίες να τις ποστάρει εδώ?
Ειδικά στις ακολουθίες έχω πρόβλημα και θέλω ένα μπούσουλα για να κάνω καμιά άσκηση...
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on August 24, 2011, 19:29:08 pm
για διευκολυνση σε τυχον προβληματα με πολικες μπειτε εδω http://www.ies.co.jp/math/java/calc/sg_kyok/sg_kyok.html
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 25, 2011, 13:17:33 pm
μιας και ειπες για πολικες..σε μια ασκηση του Ξενου ειχε:r=a-sinθ εδω πρεπει να παρουμε ολες τισ περιπτωσεις του α?
δηλαδη α<1 ,α>1, α=1?
γενικα οταν εχει α,θελει να εξεταζουμε ολες τις περιπτωσεις?
δηλαδη α<1 ,α>1, α=1?
γενικα οταν εχει α,θελει να εξεταζουμε ολες τις περιπτωσεις?
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on August 25, 2011, 13:49:17 pm
μιας και ειπες για πολικες..σε μια ασκηση του Ξενου ειχε:r=a-sinθ εδω πρεπει να παρουμε ολες τισ περιπτωσεις του α?
δηλαδη α<1 ,α>1, α=1?
γενικα οταν εχει α,θελει να εξεταζουμε ολες τις περιπτωσεις?
βασικα αυτο που καταλαβα κανοντας προχειρα κατι γραφικες παραστασεις με αυτο απο πανω που ποσταρα ειναι οτι οσο αυξανει το α κατα απολυτη τιμη το πανω μερος του σχηματος γινεται πιο πλακουτσωτο ενω για α=1 ειναι σαν καρδουλα :Pδηλαδη α<1 ,α>1, α=1?
γενικα οταν εχει α,θελει να εξεταζουμε ολες τις περιπτωσεις?
τωρα στα θεματα δεν ξερω πως ακριβως τα θελει,δεν θυμαμαι και πως τα καναμε στην ταξη :-\
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 25, 2011, 17:56:30 pm
ok thnx! ;)
γενικα ξερει κανεις αν θα υπαρχει κανενα τυπολογιο στις εξετασεις?ειναι ενας τυπος σελ 246 νομιζω που δεν παιζει να τον μαθω με τιποτα ομως... :o
γενικα ξερει κανεις αν θα υπαρχει κανενα τυπολογιο στις εξετασεις?ειναι ενας τυπος σελ 246 νομιζω που δεν παιζει να τον μαθω με τιποτα ομως... :o
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on August 25, 2011, 19:12:27 pm
ok thnx! ;)
γενικα ξερει κανεις αν θα υπαρχει κανενα τυπολογιο στις εξετασεις?ειναι ενας τυπος σελ 246 νομιζω που δεν παιζει να τον μαθω με τιποτα ομως... :o
δεν παιζει να βαλει τετοιο τυπο!αυτο που καταλαβα ειναι οτι βαζει τσιμπημενα ολοκληρωματα με τν εννοια οτι πρεπει να εχεις τα ματια σου ανοιχτα για σημεια ασυνεχειας και τετοια κ οτι σαν μεθοδολογια δν ειναι κατι που χρειαζεται την τρλη απομνημονευση!και ολοι οι τυποι για τα εμβαδα,στερεα κλπ θα δινονται..τον ιανουαριο παντως δινονταν!γενικα ξερει κανεις αν θα υπαρχει κανενα τυπολογιο στις εξετασεις?ειναι ενας τυπος σελ 246 νομιζω που δεν παιζει να τον μαθω με τιποτα ομως... :o
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 25, 2011, 19:25:03 pm
ωραια αντε να δουμε..(παντως θα ειναι γελιο να κοπω λογισμο Ι οταν εχω περασει λογισμο ΙΙ ;D ;D)
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on August 25, 2011, 20:17:06 pm
ωραια αντε να δουμε..(παντως θα ειναι γελιο να κοπω λογισμο Ι οταν εχω περασει λογισμο ΙΙ ;D ;D)
περασες λογισμο 2? :oπερνα να κανεις και κανενα ιδιαιτερο κ σε μας! ;D
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 25, 2011, 23:16:06 pm
ωραια αντε να δουμε..(παντως θα ειναι γελιο να κοπω λογισμο Ι οταν εχω περασει λογισμο ΙΙ ;D ;D)
περασες λογισμο 2? :oπερνα να κανεις και κανενα ιδιαιτερο κ σε μας! ;D
για να καταφερω να το περασω αφησα διαφορικεςθερμοδυναμικη και πιθανοτητες :'( και παρακολουθησα ολες τις διαλεξεις του καππου:o
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: teslaaaa on August 25, 2011, 23:39:22 pm
ωραια αντε να δουμε..(παντως θα ειναι γελιο να κοπω λογισμο Ι οταν εχω περασει λογισμο ΙΙ ;D ;D)
περασες λογισμο 2? :oπερνα να κανεις και κανενα ιδιαιτερο κ σε μας! ;D
για να καταφερω να το περασω αφησα διαφορικεςθερμοδυναμικη και πιθανοτητες :'( και παρακολουθησα ολες τις διαλεξεις του καππου:o
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 28, 2011, 17:53:23 pm
κατι τυπους για υπολογισμο ογκων/εμβαδων επιφανειων πρεπει να τους ξερουμε απ' εξω? :o
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Bazinga on August 28, 2011, 17:57:05 pm
ο ξενος τους δινει και ο ροθος νομιζω δε τα εχει καν στην υλη.
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: johnvoyager on August 28, 2011, 18:01:57 pm
thnx for the info! ;)
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: geralt on January 28, 2012, 13:37:52 pm
Καποιος παλιος μπορει να το δωσει με τον Ροθο αντι του Ξενου? Εγω ημουν στο τμημα του Ξενου.
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Αιμιλία η φτερωτή χελώνα on January 28, 2012, 16:31:27 pm
ναι διαλεγεις εσυ αν εισαι παλιος
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: hetfield on January 30, 2012, 17:22:57 pm
ορια του στυλ lim[(n+1)/n]^n που δινει e και γενικα αλλα ορια οπως lim ln(n+1)/ln(n) που κανει 1,lim[(sin(f(n)))^k/f(n)^k] που δινει 1 κλπ,τα παιρνουμε ετοιμα η πρεπει να αποδειξουμε οτι κανουν τοσο??
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: 4emonas on January 30, 2012, 22:50:59 pm
θεματα ροθου εχουμε?
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: alekos789 on January 30, 2012, 23:44:51 pm
στο κριτιριο cauchy αν το οριο βγει +απειρο σημαινει οτι η σειρα αποκλεινει η πρεπει το οριο να ειναι πεπερασμενος αριθμος?
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Rothos on January 21, 2013, 22:26:06 pm
ΛΟΓΩ ΑΣΘΕΝΕΙΑΣ ΑΝΑΒΑΛΛΕΤΑΙ ΤΟ ΑΥΡΙΑΝΟ ΜΑΘΗΜΑ 9-11.
ΒΑΣΙΛΗΣ Μ ΡΟΘΟΣ
ΒΑΣΙΛΗΣ Μ ΡΟΘΟΣ
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Rothos on January 23, 2013, 15:13:40 pm
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ 2 sto ethmmy
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: electric67 on September 01, 2013, 18:20:22 pm
στις χειρογραφες λυσεις του ροθου στην τελευται σελιδα τελευταια ασκηση πρεπει να χει λαθος, ειναι θετικη η σειρα
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: airguitar on January 22, 2014, 22:38:16 pm
Αμα εχουμε μια δυναμοσειρα και μας ζητα να εξετασουμε την συγκλιση.
και βρουμε οτι το οριο της στο απειρο ειναι μηδεν τοτε συγκλινει ???
και βρουμε οτι το οριο της στο απειρο ειναι μηδεν τοτε συγκλινει ???
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Kthulu on June 20, 2014, 17:39:30 pm
Ολοκλήρωμα sqrt(1+cosx)dx και
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: c0ndemn3d on June 20, 2014, 17:46:02 pm
Ολοκλήρωμα sqrt(1+cosx)dx και
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Χωρίς να είμαι σίγουρος:
το πρώτο γράψε cosx = 1 - 2cos^2(x/2)
το δεύτερο θέσε t = sinq και μετά ακολουθείς τη διαδικασία του βιβλίου για τα τριγωνομετρικά ολοκληρώματα
edit: Όντως μου ξέφυγε το 2
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: Kthulu on June 20, 2014, 18:01:52 pm
Ολοκλήρωμα sqrt(1+cosx)dx και
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Ολοκλήρωμα (1-t^2)^k dt
πως βγαινουν;;
Χωρίς να είμαι σίγουρος:
το πρώτο γράψε cosx = 1 - cos^2(x/2)
το δεύτερο θέσε t = sinq και μετά ακολουθείς τη διαδικασία του βιβλίου για τα τριγωνομετρικά ολοκληρώματα
Έγινε!( στο πρώτο μάλλον εννοείς cosx = 1 - 2cos^2(x/2) )
Σε ευχαριστώ!
Title: Re: [Λογισμός Ι] Παλιά θέματα - Σχολιασμός και απορίες
Post by: George_RT on June 21, 2014, 16:54:40 pm
Μήπως θυμάται κανείς τι τυπολογία έδινε ;